无刷双馈电机转子优化的最优点参数解耦法

夏 野，边 涛，朱景伟

(1.大连海事大学，大连 116026， 2.国网铁岭供电公司， 铁岭 112000)

无刷双馈电机转子优化的最优点参数解耦法

夏 野1，边 涛2，朱景伟1

(1.大连海事大学，大连 116026， 2.国网铁岭供电公司， 铁岭 112000)

摘 要：针对无刷双馈电机转子优化设计没有准确实现的方法，研究了最优点参数解耦法。对凸极磁障式转子进行了优化设计，得出了相应凸极磁障式转子对磁场调制能力最强的参数组合。通过与圆形片磁障式转子对比，得出了凸极磁障式转子输出电压幅值高、但对磁场调制能力弱的结论，也间接证明了最优点参数解耦法的可行性与正确性，为无刷双馈电机转子的开发提供了一种现实可行的优化方法。

关键词：无刷双馈电机；优化设计；最优点参数解耦法；凸极磁障式转子

0 引 言

无刷双馈电机(以下简称BDFM)是一种同时具有同步电机和异步电机特点的新型电机，不但和传统笼型转子感应电机一样，结构简单，坚固耐用，转子上取消了电刷和滑环，提高了运行安全性和可靠性，减少了维修成本，而且具有良好的起动和运行特性，能方便地实现异步、同步、双馈和变速恒频发电等多种运行方式。因此，BDFM在传统交流调速系统，以及风力、水力系统的变速恒频发电领域前景广阔，研究BDFM具有重要的理论意义和应用价值[1]。

目前对BDFM的优化设计主要集中在对转子的研究上，文献[2]对凸极式、笼型和圆形片磁障式转子进行了对比分析，得出了圆形片磁障式转子对磁场调制能力最强，凸极式次之的结论。文献[1]对方形片磁障式转子进行了研究，并在其基础上加入笼条，进一步优化了该类转子对磁场的调制能力。在对BDFM优化设计研究的论文中基本都会出现不同形式转子电机性能的对比分析，但如何在确定转子形式后，获得该类转子的最优物理结构，即获得对磁场调制能力最优的此类转子，还没有论文提出过具体方法，而在不同形式转子无法同时达到最优性能点的情况下，对它们的性能作横向对比分析，所得出的结论也显得缺乏说服力，甚至可能会影响BDFM的整体开发进度。针对此问题，本文研究了最优点参数解耦法，并结合优化实例，选择目前还没有在文献中被详细分析过的凸极磁障式转子BDFM进行具体优化设计与研究。

1 BDFM的转子

BDFM定子设计方法与传统交流电机区别不大，改进空间有限,因此，目前BDFM的优化设计主要集中在对转子的研究上。作为重要的“极数转换器”，转子对2套定子绕组磁场的调制能力甚至直接决定着BDFM整体性能的优劣。

1.1 转子转速

BDFM的定子上嵌放有2套彼此独立的三相绕组，其中一套是极对数为pp的功率绕组，它直接与电网连接，其频率fp恒定；另一套是极对数为pc的控制绕组，由变频电源供电，其频率fc可调。定子功率绕组和控制绕组在理论上没有直接耦合，而是通过转子的磁场调制作用来实现机电能量的转换[3 - 4]。

转子转速表达式[1]：

(1)

理论上，在变频器输送频率固定后，电机的转速即可确定，转速控制十分精确。

1.2 常见转子

目前，比较常见的BDFM转子结构如图1所示。其中，凸极式转子和笼型转子的结构简单、易于制造、成本低，但对磁场的调制效果都比较差，谐波含量高，效率较低；磁障式转子通过限制磁路来实现对磁场的调制，目前比较常见的形式有圆形片和方形片2种。磁障式转子又可分为轴向叠片式和径向叠片式，轴向叠片式虽然工艺相对更易实现，但存在较大的涡流损耗；径向叠片式则克服了这一缺点，且对磁场调制效果优于凸极和笼型转子，是目前最受关注的一种BDFM转子结构，特别是方形径向叠片磁障式转子，它可以加入笼条，进一步优化了调制性能。

(a) 凸极式转子

(b) 笼型转子

(c) 圆形片磁障式转子

(d) 方形片磁障式转子

2 最优点参数解耦法

目前，对BDFM各类转子优化设计的方法基本都是先选定转子参数，并分别对这些参数进行分析，得出每个参数的最优值，然后将这些最优值组合，得出最优的转子结构。但此过程无法保证各个参数之间没有耦合影响，即某一个参数变化后，另一个参数的最优点是有可能发生变化的。最优点参数解耦法可以有效地解决这一问题，通过对选定参数不断地进行解耦，去除各个参数之间在最优点可能存在的相互影响，最终得出转子的最优物理结构，其基本流程如图2所示。

图2 最优点参数解耦法流程图

首先，针对BDFM已经确定的转子结构排除干扰、选定关键参数，选择这些参数的基本原则是：

a) 所选的参数尽可能得少；

b) 所选的参数尽量在物理结构上不互相干预；

c) 所选参数必须能完全限定该转子的物理结构形式，即参数值全部确定后，转子可以明确地设计出来。

选择好参数后，从中选定任意一个作为1号参数，在保证其他参数符合基本工艺要求并完全相同的条件下，对1号参数设定不同的分布值，经仿真分析得出对磁场调制能力最强的1号参数。再选定2号参数，在1号参数最优、其他参数与前次仿真相同的情况下进行2号参数的分布分析，得出最优的2号参数。接下来在2号参数最优、其他参数与前次仿真相同的情况下，再次对1号参数进行分布分析，如果1号参数的最优点基本没有变化，说明1号和2号参数在目前的最优点无相互影响；如果1号参数的最优点发生偏移，证明1号和2号参数之间存在比较大的相互影响，那么在新的最优1号参数情况下再次对2号参数进行分布分析，不断重复这一过程，直至得到最优点不再发生偏移的1号和2号参数。此过程称之为1号与2号参数的解耦。

之后不断引入新的参数进行解耦，基本原则是只要有某一参数最优点在解耦过程中发生偏移，就回到本次解耦的初始点，进行重新解耦。此方法可以确保各个参数同时达到对磁场调制能力最有利的值，即实现转子的最优化。

3 最优点参数解耦法实例分析

本文使用最优点参数解耦法对一台小型轴带无刷双馈发电机进行优化设计，电机主要参数如表1所示。

表1 电机主要参数

转子结构形式选择凸极磁障式，如图3所示。这类转子由于凸极处没有磁隔离，会对自身的磁场调制能力有所影响，但其实际性能如何，目前并没有文献进行过研究。本文将使用最优点参数解耦法，对此转子进行具体优化设计。

图3 凸极磁障式转子

3.1 分析方法

针对此优化设计案例，本文利用二维有限元瞬态场进行仿真、对比和分析。基本思路是按设计要求固定控制绕组的励磁输入，并由式(1)确定相应的转子转速。在确保励磁输入和转子转速不变的情况下对不同的模型进行有限元计算，统计3个主要参数：功率绕组输出相电压幅值、气隙磁场中2次谐波含量、气隙磁场中3次谐波含量。根据文献[5]对BDFM气隙磁场分布的分析，这3个量越大，说明转子的调制能力越强。

本文采用的数据分析方式：在MATLAB中编写程序，对有限元仿真运算得来的气隙磁场分布图作傅里叶分解，得出气隙磁场中各次谐波的分布。

3.2 排除干扰

在选定该转子参数前，首先应排除一些对参数选择有影响的干扰。在本文优化设计中，影响参数选择的主要因素有2个：小导磁片是否应该等宽；外围5个小凹陷处是否应该有导磁片。

针对这2个问题进行二维有限元瞬态场对比分析，由于这并不是本文主要研究内容，所以直接给出结论：

导磁片不等宽对转子调制能力影响不大，考虑工艺实现的复杂程度，本文采用等宽的导磁片；5个小凹陷处有导磁片虽然会使输出相电压幅值略有提高，但明显增加谐波含量，影响输出波形效果。因此，本文选择不在此处加小导磁片。

3.3 关键参数选择与解耦

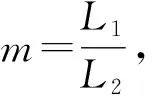
图4 参数示意图

3.3.1 参数d,m的设计与解耦

取h=18 mm,m=2,a=0.2,b=0.1，对不同d值的电机模型进行二维瞬态场有限元分析结果如表2所示。

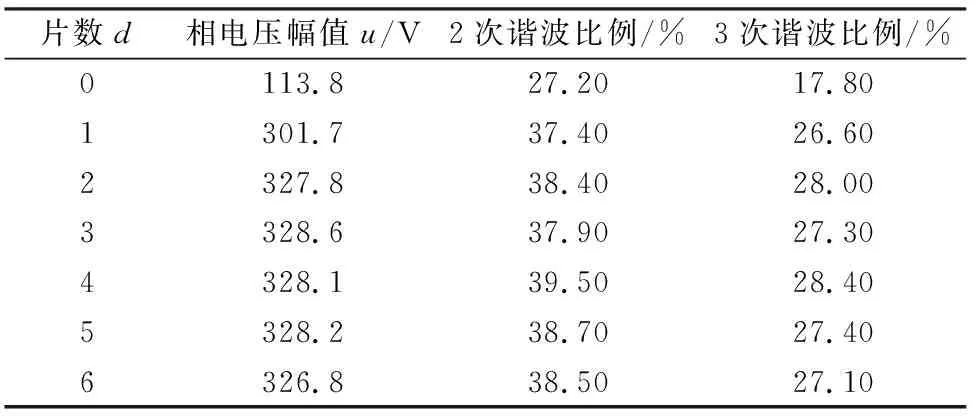
表2 参数d最优值仿真结果

综合考虑气隙中有用次谐波含量、输出相电压幅值及工艺因素，取d=2较为适合。

取h=18mm,d=2,a=0.2,b=0.1，对不同m值的电机模型进行二维瞬态场有限元分析结果如表3所示。

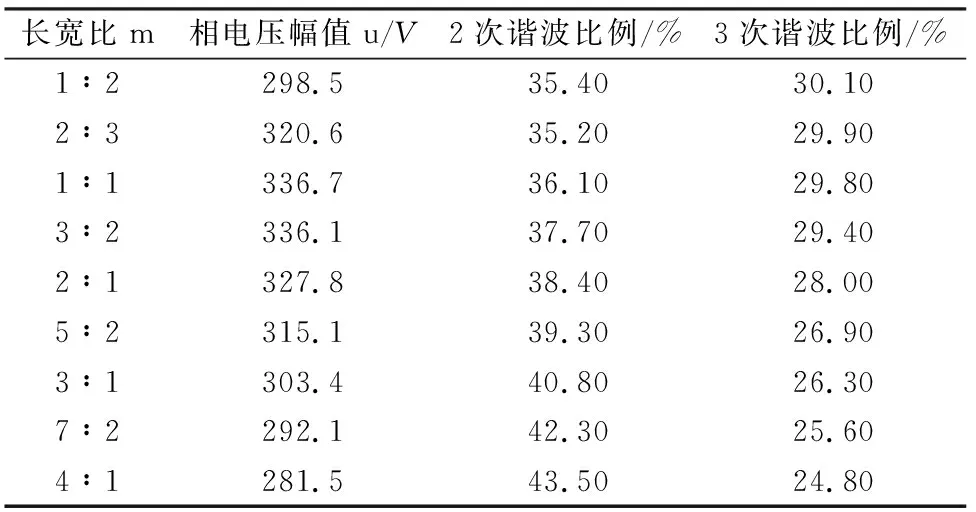
表3 参数m最优值仿真结果

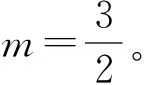
表4 参数d,m解耦仿真结果

3.3.2 参数d,m,h的设计与解耦

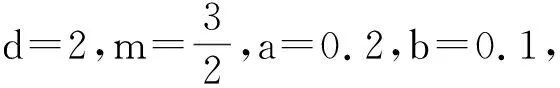
表5 参数h最优值仿真结果

最优值取h=30 mm。

对参数h和d,m进行解耦：取h=30 mm,d=2,a=0.2,b=0.1，对不同m值的电机模型进行二维瞬态场有限元分析结果如表6所示。

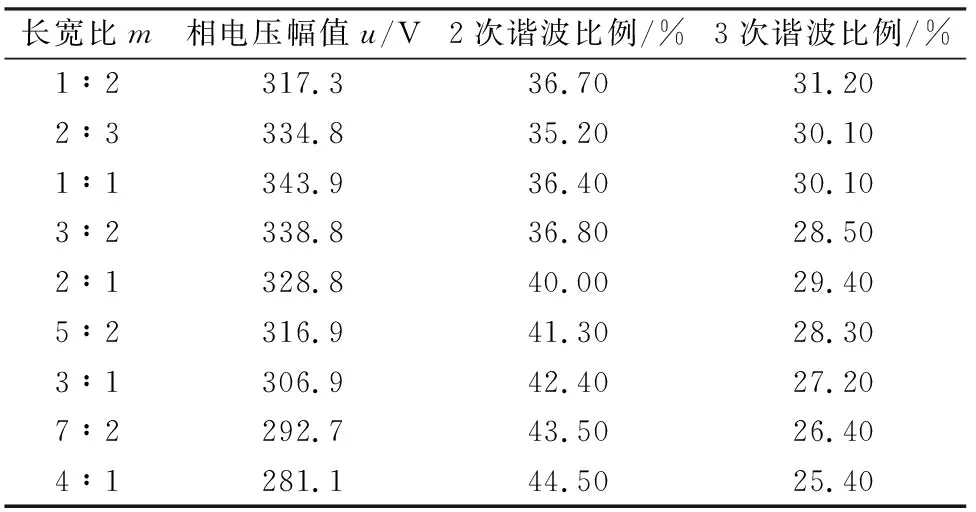
表6 参数m一致性检验仿真结果

取d=2,m=1,a=0.2,b=0.1，对不同h值的电机模型进行二维瞬态场有限元分析，发现h的最优值仍取30mm。

取h=30mm,m=1,a=0.2,b=0.1，对不同d值的电机模型进行二维瞬态场有限元，发现d的最优值仍取2。

以上说明参数d,m与h已在最优点实现解耦，同时达到最优值。

3.3.3 参数d,m,h,a,b的设计与解耦

由于参数a和b直接决定着转子表面导磁部分的分布，因此它们可以看成一个整体参数进行分析，提高优化效率。即先进行参数a和b的设计与解耦，再与另外3个参数进行解耦。

取d=2,m=1,h=30mm,a=0.2，对不同b值的电机模型进行二维瞬态场有限元分析结果如表7所示。

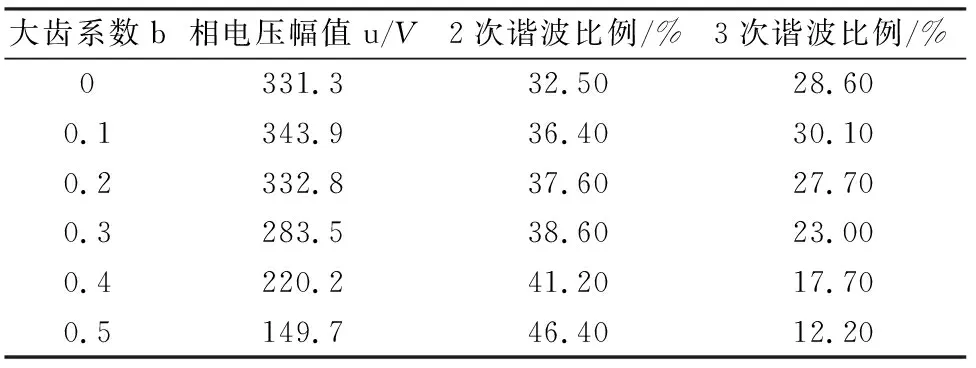
表7 参数b最优值仿真结果

最优值取b=0.1。

取d=2,m=1,h=30 mm,b=0.1，对不同a值的电机模型进行二维瞬态场有限元分析结果如表8所示。

表8 参数a最优值仿真结果

最优值取a=0.3。

对参数a和b进行解耦：取d=2,h=30mm,m=1,a=0.3，对不同b值的电机模型进行二维瞬态场有限元分析发现，在a取最优值时，b=0.1仍然是符合设计要求的最优点，说明参数a与b已在最优点实现解耦，同时达到最优值。

对参数a,b和d,m,h进行解耦：取h=30mm,m=1,a=0.3,b=0.1，对不同的d值电机模型进行二维瞬态场有限元分析；取h=30mm,d=2,a=0.3,b=0.1，对不同m值的电机模型进行二维瞬态场有限元分析；取d=2,m=1,a=0.3,b=0.1，对不同h值的电机模型进行二维瞬态场有限元分析。发现在参数a,b取最优值时，h=30mm,m=1,d=2仍然符合设计要求的最优点，说明参数a,b与h,m,d已在最优点实现解耦，同时达到最优值。

3.4 优化结果分析

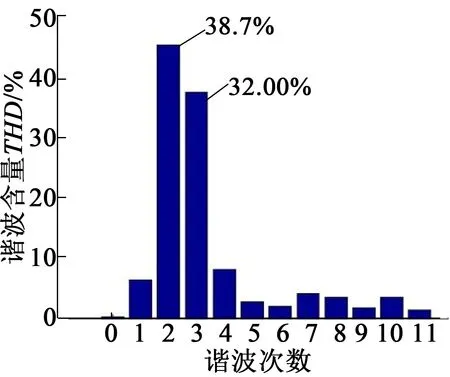
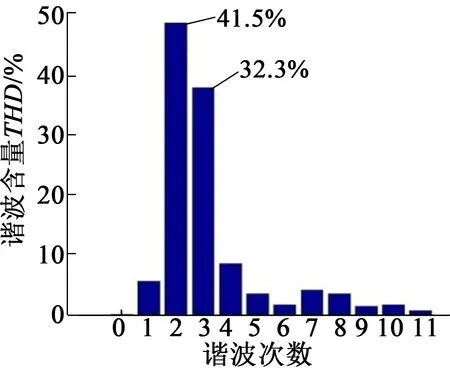
整个优化过程使用最优点参数解耦法，得出了本文凸极磁障式转子对磁场调制能力最强的参数组合：h=30mm,m=1,d=2,a=0.3,b=0.1。当然可以通过进一步细化参数分布值得出更为精确的优化结果，但本文设计精度已经基本满足，细化参数已不会使3个指标量有很大的增幅。按此参数在二维有限元瞬态场环境下绘制电机模型，并与经过大量反复实验得出的采用圆形片磁障式转子的实例最优电机模型进行仿真对比，如图5所示，2个模型除转子结构形式不同外，定子、励磁输入、转速等其他条件完全相同。经仿真计算后功率绕组输出的反电动势波形和数据分析结果分别如图6和图7所示。

(a) 凸极磁障式转子

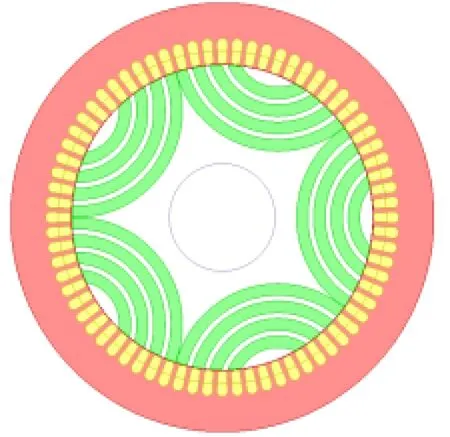
(b) 圆形片磁障式转子

(a) 凸极磁障式转子

(b) 圆形片磁障式转子

(a) 凸极磁障式转子

(b) 圆形片磁障式转子

对比分析结果可以发现，在此小型轴带发电机的优化设计中，采用凸极磁障式转子会使输出电压幅值略高于采用圆形片磁障式转子的情况，但有用次谐波含量却低于圆形片磁障式转子，输出谐波含量高，对磁场调制能力差，效率较低。这主要是因为凸极处没有磁隔离造成的，与实际理论相符。

4 结 语

本文研究了一种针对BDFM转子优化设计的实用方法，即最优点参数解耦法，并利用此方法首次对凸极磁障式转子进行了分析与优化，找到了相应凸极磁障式转子的最优参数组合，并得出结论：凸极磁障式转子虽然在输出幅值方面高于圆形片磁障式转子，但对磁场的调制能力要低于圆形片磁障式转子，间接证明了最优点参数解耦法的可行性与正确性。

目前，对BDFM的优化设计研究仍主要集中在发现结构更简单且对磁场调制能力更强的转子，最优点参数解耦法将有助于发掘BDFM各类结构形式转子的最优性能点，是一种现实可行的方法，也希望它能对BDFM未来的研究和发展有所帮助。

[1] 王秀平.新型混合转子BDFM的电磁特性分析与实验研究[D].沈阳：沈阳工业大学,2014.

[2] 薛冰,胡堃,樊贝.不同转子结构无刷双馈电动机的仿真研究[J].工矿自动化,2012,38(1):55-58.

[3]WILLIAMSONS,FERREIRAAC,WALLACEA,etal.Generalisedtheoryofthebrushlessdoublyfedmachine.I.Analysis[J].IEEProceedingsElectricPowerApplications,1997,144(2):111-122.

[4] 杨俊华,吕惠子,吴捷,等.基于波波夫超稳定性的BDFM直接转矩控制[J].中国电机工程学报,2009(15):107-113.

[5] 张千.径向叠片磁阻转子无刷双馈电机的有限元分析与研究[D].北京：北京交通大学,2010.

DecouplingMethodforOptimalPointParametersofBrushlessDoublyFedMachinesRotorOptimize

XIAYe1,BIANTao2,ZHUJing-wei1

(1.Dalian Maritime University,Dalian 116026,China;2.Tieling Power Supply Company of State Grid,Tieling 112000,China)

Abstract:Aiming at the current problem of having no accurate and effective method in brushless doubly fed machines rotor design, decoupling method for optimal point parameters was put forward. The salient pole and magnetic barrier rotor was optimized and designed for the first time and the corresponding best parameters combination of salient pole and magnetic barrier rotor for magnetic field modulation ability was got. According to the comparison with magnetic barrier rotor, the conclusion was reached that salient pole and magnetic barrier has higher output voltage amplitude, but weaker magnetic field modulation ability, which also indirectly proved the feasibility and correctness of the decoupling method for optimal point parameters. It will provide a practical and feasible optimization method for the development of brushless doubly fed machines rotor.

Key words：brushless doubly fed machines(BDFM); optimum design; most advantage parameters decoupling method; salient pole and magnetic barrier rotor

中图分类号：TM351

A

1004-7018(2018)05-0039-05

2016-07-12

中央高校基本科研业务费资助项目(3132016313)

作者简介：夏野(1988—)，男，硕士研究生，研究方向为无刷双馈电机的设计与优化。