铣削面加工误差预测变异模型研究*

刘守法 周美丽 王晋鹏

(①西京学院机械工程学院，陕西 西安 710123；②延安大学物理与电子信息学院，陕西 延安716000；③西北工业大学机电学院，陕西 西安 710072)

德国提出的“工业4.0”驱动新一轮工业革命，在此背景下，“中国制造2025”成为中国工业未来10年的发展纲领和顶层设计，围绕创新驱动、智能转型、绿色发展，中国将在国际合作中进一步提升国家制造业水平[1-3]。随着世界先进制造技术不断兴起，超高速切削、超精密加工等技术的应用，柔性制造系统的迅速发展和计算机集成系统的不断成熟，对数控加工技术提出了更高的要求。从技术层面来讲，加速提高机床精度成为解决机床制造业持续发展的一个关键[4-6]。

铣削加工是机床加工行业不可或缺的一种重要加工方式，利用端面铣加工叶片类较薄零件时，去除大量材料导致加工精度不稳定。传统的解决方法是利用试错法获得较稳定的精度，但这种方法会延长生产周期、增加成本。如何集成引起误差和各种原因，通过建立模型预测铣削加工件的误差成为一个重要研究方向[7-10]。

作者针对端面铣削工艺，集成了刀具和工件变形、刀具偏摆和机床空间误差等影响因素，建立了铣削加工面加工误差预测变异模型，用来预测端面铣削加工件的加工误差。通过与实验对比，验证了该模型的准确性。可对铣削加工误差进行预测，为刀具补偿提供参考，有利于缩短产品生产周期。

1 铣削面加工误差模型

针对端面铣削加工工艺，建立不同切削高度的加工误差及其变异模型。需假设模型在稳态和准静态切削状态下进行推导与验证；将铣削过程简化为径向切削深度方向的单一自由度系统。

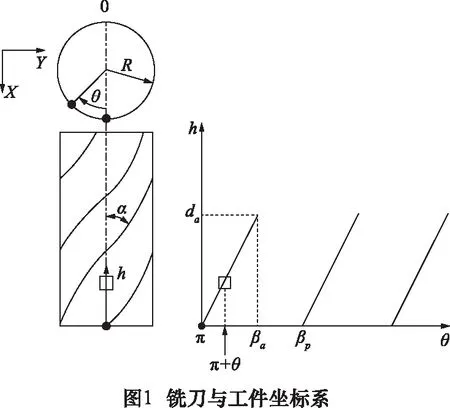
图1所示为铣刀的圆柱坐标和工件的笛卡尔坐标系统，在顺铣切削时，刀具底部切削点切削至坐标π 时开始在加工面产生表面形貌，铣刀再旋转角度θ，工件形貌生成点移至图中方块位置。将形貌生成点高度h与刀具旋转角度的关系表示为：

(1)

式中：k=1,2,3，…，∞，(k-1)βp≤θ≤(k-1)βp+βa；βa为铣削坐标点高度h由0上升到da时刀具的转角；βp为相邻刀尖间间隔角度。

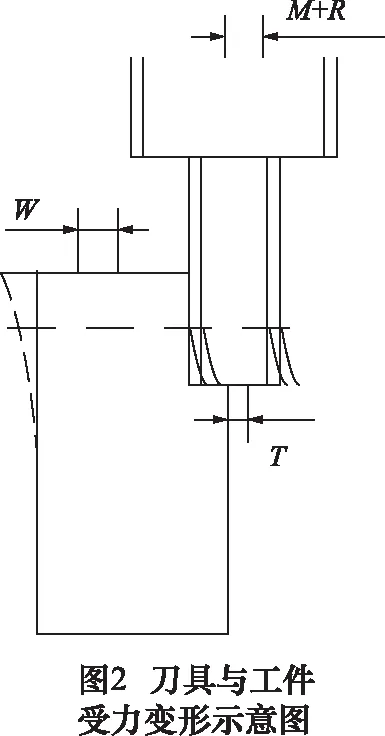
图2所示为实际铣削中刀具与工件变形状态，铣削力F引起的工件变形W、刀具变形T、刀具偏摆R和机床空间误差M是引起加工件加工误差Oc的主要原因。只考虑垂直于x进给方向的单一自由度加工误差，Oc可由上述因子线性叠加表示为

Oc(x,h)=T(h)+W(h)+R(h)+M(x)

(2)

式中：x为进给坐标；h为形貌生成点高度。因工件变形T与刀具变形W受的动态铣削力大小相同且方向相反，将T和W两个参数合并为加工误差P，P为动态铣削力F与综合刚度K的比值。公式(2)可简化如下：

Oc(x,h)=P(h)+R(h)+M(x)

(3)

1.1 刀具受力变形分析

由于铣削过程中铣削力呈周期变化，在时域中是角度的函数。刀具受力变形量也随着铣削力的变化而呈周期性变化。将刀具视为悬臂梁，如图3 所示。轴向切深较浅情况下，利用悬臂梁公式表示刀具刚度kt为：

(4)

式中：E为刀具杨氏模量；I为惯性矩；L为刀具长度。刀具的变形量表示为：

T(θ)=F(θ)/Kt

(5)

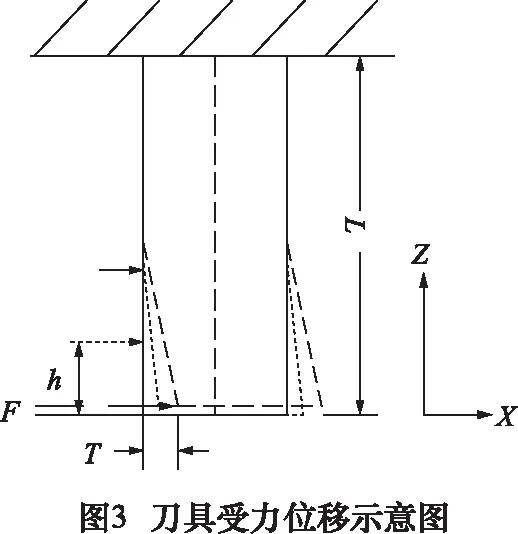
图4为顺铣后产生表面形貌的示意图，只有刀刃转过角度π后，刀刃尖点才会划过工件铣削面，留下加工痕迹，且轴向切深从高度零处开始产生，铣刀转过一定角度后，刀刃铣削至轴向深度da处离开加工面。顺铣时真正产生表面形貌的区间为π～π+βa，定义其表面生成窗函数为：

(6)

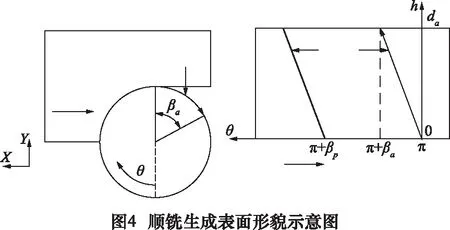
在产生表面形貌区间，刀具受力变形量表示为T(θ)=F(θ)/Kt·S(θ) ，又因θ=(h·tanα)/R，刀具受力变形量表示为T(h)=F(h)/Kt·S(h)。

1.2 工件受力变形分析

铣削时，使工件产生变形，导致加工误差。由于工件是由夹具固定在工作台上，单纯使用简单力学公式求工件刚度往往与实际敲击测量或静态受力测量有较大误差。本实验采用敲击测量求得工件准静态刚度，利用多次敲击工件铣削处所得测量结果的平均值代表工件准静态刚度Kw，则工件变形量表示为：

W(θ)=F(θ)/Kw

(7)

工件变形引起的加工误差与刀具变形引起的加工误差方向相反，故将表面生成窗函数代入式(7)，并用h代替θ得：

W(h)=F(h)/Kw·S(h)

(8)

1.3 刀具偏摆分析

测量刀具偏摆时，位移计架设在铣削坐标180°位置，与工件同方向，刀具底部的刀刃位置也要在同一地方，使主轴低速旋转测量其偏摆值，利用电容式位移计取样频率fs表示不同轴向切深的刀具偏摆量R(h)=R·(hK/da) ·(βa/2π) ·fs。

1.4 加工件加工误差变异模型

由于受工作台随机误差、工作台动态特性、切削热、材料各向异性和积屑等影响，实际加工过程中铣削面上同一高度处加工误出现差异。

根据误差传递概念建立的加工误差函数式(2)中，M、T、W和R的传递系数均为1。因各因子间的关系对误差传递计算结果有直接影响，因此需要求出各个因子的相关系数。假设n对变量分别为(x1,y1),(x2,y2),…,(xn,yn)，则两变量x,y的相关系数定义为

(9)

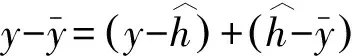
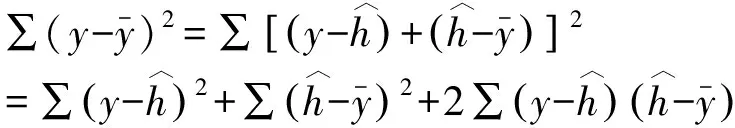
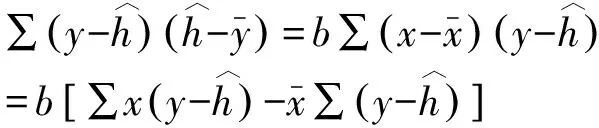
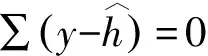
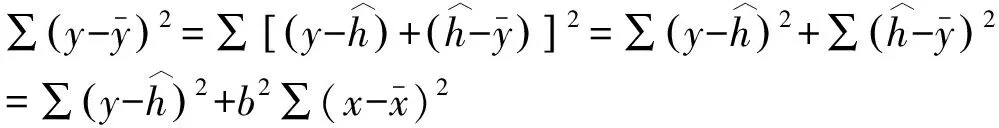
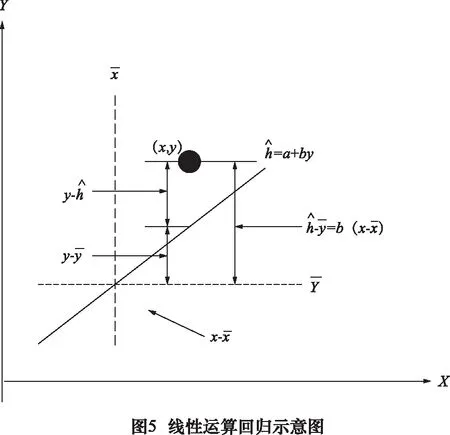
如果x和y互为高度正相关，则SSE为极小。判定系数为：

(10)

该值为较客观的拟合程度指标，式中0≤ρ2≤1，ρ2越大，显示x提供的信息对y越有用。

将加工误差Oc=f(M,T,W,R)表示为多元函数，刀具受力变形(T)与工件受力变形(W)完全线性相关，由过程误差P表示。在误差项与其影响因子变动具有随机性且其变动数值不可预知情况下，加工误差函数的变动量可由函数的全微分方程求得：

(11)

(12)

经过误差的多次测量，将Δ表示为δ，并将各个方程式两边平方可得：

(13)

将方程组(13)中各方程式相加可得加工误差函数Oc的随机变动与各因子随机变动的关系为：

(14)

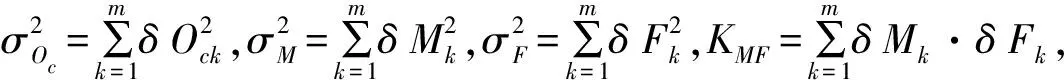
将式(14)两边除以m并开根号得到加工误差变异模型。

(15)

式中：ρMF表示工作台误差影响因子与过程误差影响因子间的相关系数。根据(15) 式可以由各影响因子的标准差计算出工件加工误差函数的标准差。

2 实验验证

实验用铣削材料为6061-T6铝合金，尺寸为40 mm×20 mm×80 mm3，刀具材料为碳化钨螺旋立铣刀，刀具伸出长度L、直径D、螺旋角、齿数和弹性模量E分别为35 mm、10 mm、30°、4和206×109Pa。

实验中使用的机床为SINUMERIK 808D型和JOHNFORD VMC-850型铣床，分别标注为A机床和B机床，A机床和B机床转速分别为2 800 r/min和1 000 r/min，两机床顺铣加工，进给速度30 mm/min，轴向切深为5 mm，背吃刀量为5 mm。利用敲击法测得刀具刚度和工件刚度，并求得A机床和B机床的综合刚度分别为4.5 N/μm和2.2 N/μm。利用电容式位移传感器测量A机床刀具旋转偏摆量，铣削高度为1.5 mm、2 mm、2.5 mm和3 mm处对应的偏摆量分别为0 μm、1 μm、2 μm和4 μm。B机床的偏摆量很小可忽略。

3 讨论

在预测铣削面加工误差分布范围时，笔者提出的加工误差预测模型中引入了铣削力、机床空间误差和刀具偏摆3个因素的影响。误差预测模型的拟合程度由判定系数来判断，用一个数据来解释另一个数据的变异比例。表1所示为各实验状态对应的相关系数及其判定系数，且判定系数均大于0.9，可见用力数据变异来预测铣削面加工误差变异有90%以上的可信度。

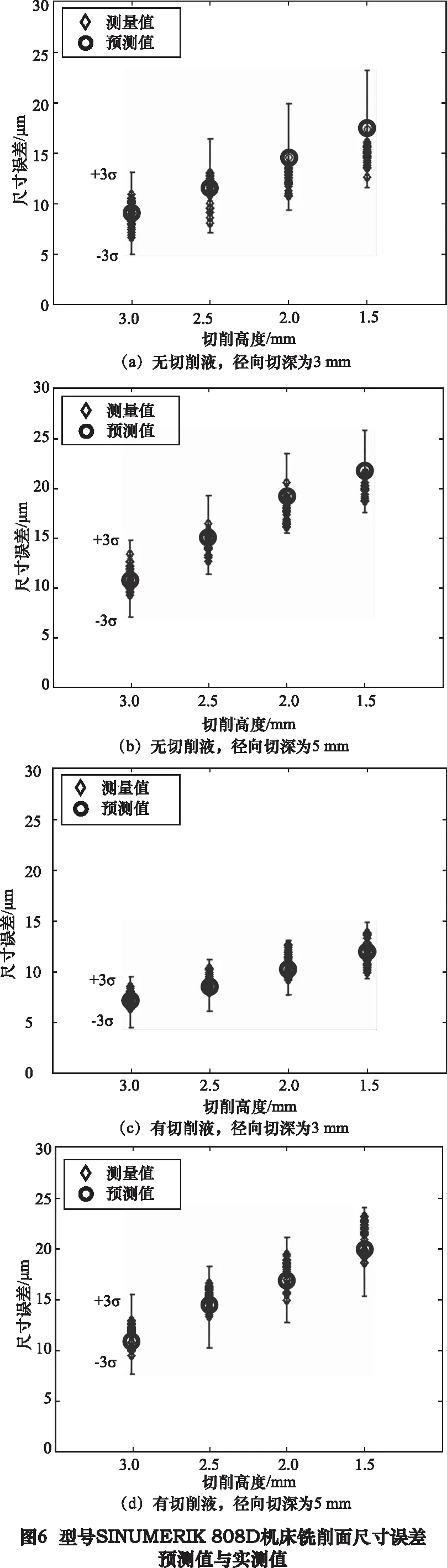
图6所示为SINUMERIK 808D机床铣削面尺寸误差预测值与实测值。实测值菱形表示、预测值圆圈表示，预估的加工误差分布范围为对应的上下边界，可见所有预测值位于实测值范围内。

表1 各实验状态对应的相关系数及其判定系数

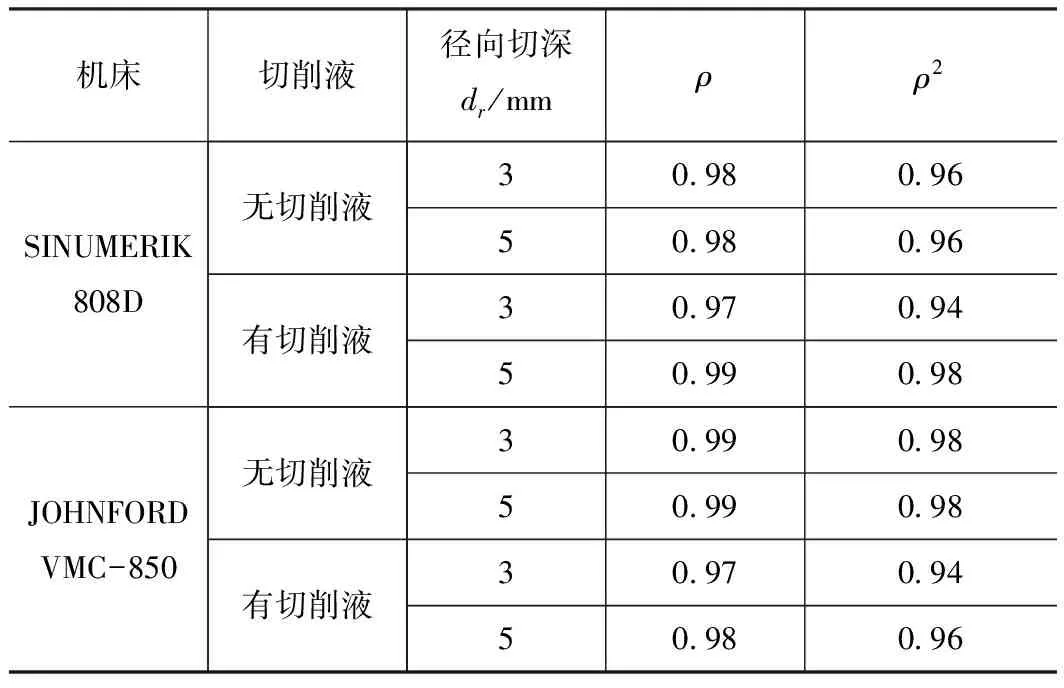
机床切削液径向切深dr/mmρρ2SINUMERIK 808D无切削液有切削液30.980.9650.980.9630.970.9450.990.98JOHNFORD VMC-850无切削液有切削液30.990.9850.990.9830.970.9450.980.96

4 结语

(1)对实验结果估算出的判定系数大于0.9，可知该模型对铣削加工误差的预测可信度达到了90%以上。

(2)经实验验证，笔者提出的端铣面加工误差预测模型能够正确预测铣削面尺寸误差及其随机分布范围。

[1] 刘坤华, 钟佩思, 李珊珊,等. 智能车间及智能车床的研究[J]. 机床与液压, 2017,45(16):20-24.

[2] 李杰林, 陈明. “工业4.0”制造模式下面向云服务的信息物理系统参考架构研究[J]. 现代制造工程, 2017, 40(8): 147-156.

[3] 赵钦志, 王立平, 王军见. 数控机床可靠性试验和评估技术分析与研究[J]. 制造技术与机床,2017(11):17-21.

[4] 刘守法, 周兆峰, 吴松林. 端铣加工面尺寸误差预测[J]. 机床与液压,2015,43(7):89-91.

[5] 黄奕乔, 杨建国. 数控机床体积误差激光分步体对角线测量的优化方法[J]. 组合机床与自动化加工技术,2017,58(2):54-59,64.

[6]要小鹏, 殷国富, 李光明. 数控机床进给轴综合误差解耦建模与补偿研究[J]. 机械工程学报,2016,52(1):184-192.

[7]党建卫, 张卫红, 万敏,等. 周铣过程中加工误差预测新模型[J]. 机械工程学报, 2011, 47(17):150-155.

[8]Law K M Y, Geddam A. Error compensation in the end milling of pockets: a methodology[J]. Journal of Materials Processing Tech, 2003, 139(3):21-27.

[9]Shi H R, Lee H S, Chong N C. The form error prediction in side wall machining considering tool deflection[J]. International Journal of Machine Tools & Manufacture, 2003, 43(14):1405-1411.

[10] Kang Y G, Wang Z Q. Two efficient iterative algorithms for error prediction in peripheral milling of thin-walled workpieces considering the in-cutting chip[J]. International Journal of Machine Tools & Manufacture, 2013, 73(73):55-61.