时滞变频调压供水系统的稳定性及Hopf分支性质

丁宇婷 蒋丽 苏琳琳

摘 要：为研究一类人造板施胶过程中的变频调压供水系统的数学模型，在原有线性化模型的基础上考虑了时滞的影响及非线性因素，从而得到更符合实际的时滞变频调压供水系统的非线性微分方程。进一步分析了该方程平衡点的存在性、稳定性及Hopf分支的存在性和稳定性，并利用多时间尺度方法推导系统Hopf分支的规范型。利用Matlab软件结合参数的实际意义给出数值仿真，展示了系統存在的稳定平衡点及稳定周期解，从而验证理论分析的正确性。

关键词：变频调压供水系统； 时滞； 稳定性； Hopf分支； 多时间尺度

DOI：10.15938/j.jhust.2018.02.027

中图分类号： O175.13

文献标志码： A

文章编号： 1007-2683（2018）02-0149-06

Abstract：This paper considers the mathematical model of variable frequency water supply system in the process of applying glue to artificial board. On the basis of the original linear model， the effects of time delay and the nonlinear factors are considered. Then we get the delayed nonlinear differential equation of variable frequency water-supply system. Further， we consider the existence and stability of the equilibrium and the Hopf bifurcation in this equation， and derive the normal form of the Hopf bifurcation by using the multiple time scales method. Finally， by using Matlab software， we obtain numerical simulations under actual parameters， and we show the existence of stable equilibrium and stable periodic solutions of the system to verify the correctness of the theoretical analysis.

Keywords：variable frequency water-supply system； time delay； stability； hopf bifurcation； multiple time scales

0 引 言

近年来，国内外人造板工业发展十分迅速，在不断吸收国外先进经验的基础上，国内人造板生产技术不断优化，质量不断提高，但在生产过程中仍难以摆脱对国外产品的仿制，创新部分不足。调施胶工艺是影响人造板生产的重要因素之一，该过程不仅具有多种约束条件、多变量、非线性、大时滞等特点，而且要求系统能够在一定程度上具有克服动态不确定性的能力，并且具有较好的稳定性[1-3]。

人造板调施胶系统由变频电机、泵和管道组成，学者在研究过程中，更多的是侧重调施胶工艺控制系统的研究，并且为了简便，对于控制系统基于的变频调压的数学模型，往往使用一些理想的数学模型。这样得到的模型在系统具有时间延迟，变量间具有非线性关系等非理想因素影响下，就会不准确，然而很少有学者会研究具这两类因素的数学模型[4-5]。

调施胶工艺中的变频调压供水过程对所产人造板质量的优劣有很大影响，在实际生产中通常使用工程上简单实用的变频调压供水系统的数学模型[3，6]。为了简化分析，学者们往往忽略时滞的影响，并进行线性化处理，从而得到较为简单的数学模型。但在变频调压供水系统中转矩和转速往往存在平方关系，时间上也会存在滞后；如果要提高人造板施胶的生产效率，则不能忽略非线性、时滞这些重要影响因素，否则会因为对异步电机的转速的估计误差造成变频器的供给频率与实际所需频率相差较大，进而影响到系统的施胶量和人造板的生产质量。

众所周知，在生态学、工程学、医学等众多领域中，对于许多问题的研究都可以归结为考虑微分方程的定性理论[7-14]。时滞微分方程既依赖于当前时间的状态，又依赖于过去时间的状态，因而更能有效客观的描述实际问题。时滞微分方程是具有无穷多个根的超越方程，分析平衡点的稳定性及分支的存在性较为复杂，而在研究非线性动力系统时，特别是在考虑微分方程的稳定性及分支性质时，计算微分方程的规范型却是极其重要的[15-17]。计算规范型一般有中心流形约化和多时间尺度两种方法，文[18]对于几个不同的滞后型微分方程用两种方法推导出一致的约化到三阶的Hopf分支规范型。由于多时间尺度方法不需要计算中心流形定理便可以直接运用到微分方程中，因而是计算规范型的一种有效简便的方法。本文将采取该方法推导时滞变频调压供水非线性方程的Hopf分支的规范型。

本文针对人造板调施胶过程的变频调压供水系统的数学模型问题，在原有模型基础上进行改进，引入非线性和时滞因素，建立更符合实际的变频调压供水系统的非线性时滞微分方程，从而确保变频器能够准确控制施胶流量。进一步，我们分析了该系统的平衡点的存在性、稳定性、Hopf分支的存在性及分支周期解的稳定性。最后通过Matlab数值模拟验证理论分析的正确性；可以看出改进后的模型比原有模型更符合实际，具有更好的实用价值。

1 人造板施胶过程中变频调压供水系统数学模型

1.1 原始模型介绍

工程上简单实用的变频调压供水系统的数学模型，当鼠笼式电机的供电电源的电压与频率之比始终不变时，其小偏差线性化模型为[3]：

1.2 改进后的模型

在实际变频调压供水过程中，对泵类负载，转矩与转速的平方成正比[3]，即：

并且該供水过程存在时间延迟，即转子角速度的变化率与ω（t-τ）有非线性关系，结合实际背景，我们得到如下改进后的变频调压供水系统模型：

2 改进后模型稳定性分析

2.1 平衡点的存在性及稳定性

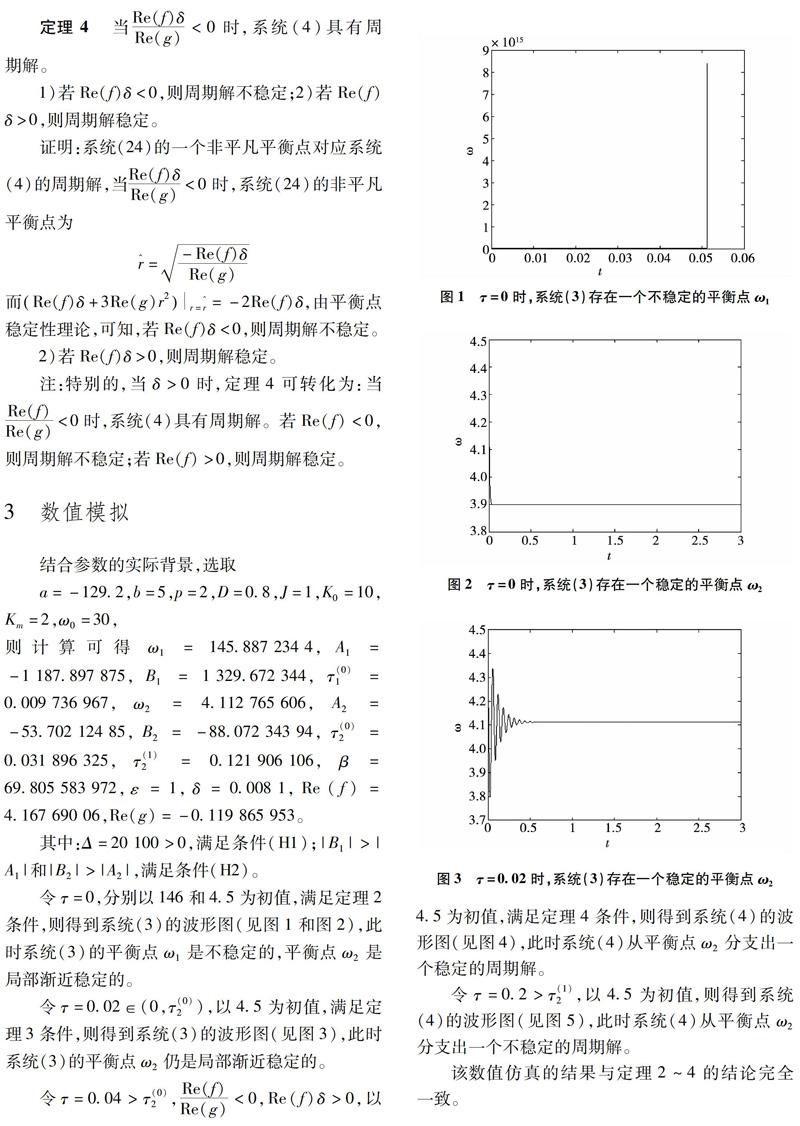
令τ=0.02∈（0，τ（0）2），以4.5为初值，满足定理3条件，则得到系统（3）的波形图（见图3），此时系统（3）的平衡点ω2仍是局部渐近稳定的。

令τ=0.04>τ（0）2，Re（f）Re（g）<0，Re（f）δ>0，以4.5为初值，满足定理4条件，则得到系统（4）的波形图（见图4），此时系统（4）从平衡点ω2分支出一个稳定的周期解。

令τ=0.2>τ（1）2，以4.5为初值，则得到系统（4）的波形图（见图5），此时系统（4）从平衡点ω2分支出一个不稳定的周期解。

该数值仿真的结果与定理2～4的结论完全一致。

4 结 论

本文研究了人造板施胶过程中的变频调压供水模型的动力学性质，将线性化的原始模型引入非线性与时滞因素，改为更符合实际的时滞微分方程模型。并分析该时滞微分方程模型的平衡点的存在性、稳定性及Hopf分支的存在性。进一步，利用多时间尺度方法推导出该系统的Hopf分支的规范型，从理论上说明引进时滞和非线性项后，系统会产生稳定的周期解。最后利用Matlab软件进行数值仿真，系统会存在稳定的平衡点，当系统经历Hopf分支后，平衡点的稳定性改变，系统会分支出稳定的周期解。数值仿真结果验证了理论分析的正确性。本文通过对实际变频调压供水系统的各个参数进行调整来控制系统的稳定性，因而改进后的变频调压供水系统的数学模型可在实际生产中起到一定指导作用。

参 考 文 献：

[1]刘德胜. 刨花板施胶动力学特性分析与鲁棒控制研究[D]. 哈尔滨：东北林业大学， 2009.

[2]孙延明，刘亚秋. 浅析中密度纤维板施胶控制研究现状[J]. 木工机床， 2006（2）：15-17.

[3]朱良宽，刘冬喆，曹军. 刨纤类人造板调施胶工艺特性分析与主参量控制模型研究[J]. 自动化技术与应用， 2013（11）：15-23.

[4]EVANS P D， MORRISON O， SENDEN T J et. al. Visualization and Numerical Analysis of Adhesive Distribution in Particleboard Using X-ray Micro-computed Tomography[J]. International Journal of Adhesion & Adhesives， 2010（30）： 754-762.

[5]HUNDHAUSEN U， MILITZ H， MAI C. Use of Alkyl Ketene Dimer （AKD）for Surface Modification of Particleboard Chips[J]. European Journal of Wood and Wood Products， 2009， 67（1）： 37-45.

[6]李婧讴. 中密度纤维板施胶系统的模糊神经网络控制器研究[D]. 哈尔滨：东北林业大学， 2014.

[7]李冬梅，刘伟华，郑忠涛. 具有预防接种且带隔离项的传染病模型的定性分析[J]. 哈尔滨理工大学学报， 2012（2）：122-126.

[8]李冬梅，李晨辰，徐亚静. 一类具有病毒变异的SEIR传染病模型的稳定性[J]. 哈尔滨理工大学学报， 2014（6）：105-109.

[9]荣智林，许俊峰，陈启军. 基波电压线性化的永磁同步电动机控制策略[J]. 电机与控制学报， 2016，20（2）：52-60.

[10]李杰，齐晓慧，刘新海，等. 改进模型参考自适应控制及其在解耦控制中的应用[J]. 电机与控制学报， 2015，19（5），112-120.

[11]WANG H， JIANG W. Hopf-pitchfork Bifurcation in van der Pols Oscillator with Nonlinear Delayed Feedback[J]. Journal of Mathematical Analysis and Applications， 2010（368）：9-18.

[12]GUO S， CHEN Y， WU J. Two-parameter Bifurcations in a Network of Two Neurons with Multiple Delays[J]. Journal of Differential Equations， 2008（244）： 444-486.

[13]HE X， LI C， HUANG T. Bogdanov-Takens Singularity in Tri-neuron Network with Time Delay[J]. IEEE Transactions on Neural Networks and Learning System， 2013， 24（6）： 1001-1007.

[14]WANG H， JIANG W， DING Y. Bifurcation Phenomena and Control Analysis in Class-B laser System with Delayed Feedback[J]. Nonlinear Dynamics， 2015， 79（4）： 2421-2438.

[15]YUAN R， JIANG W， WANG Y. Saddle-node-Hopf Bifurcation in a Modified Leslie-Gower Predator-prey Model with Time-delay and Prey Harvesting[J]. Journal of Mathematical Analysis and Applications， 2015， 422（2）： 1072-1090.

[16]XU X， YAO F， WU Q， et al. The Influence of Wax-sizing on Dimension Stability and Mechanical Properties of Bagasse Particleboard[J]. Industrial Crops and Wood Products， 2009， 29（1）： 80-85.

[17]SHEN Z， ZHANG C. Double Hopf Bifurcation of Coupled Dissipative Stuart-Landau Oscillators with Delay[J]. Appled Mathematics and Computation， 2014（227）： 553-566.

[18]YU P， DING Y， JIANG W. Equivalence of the MTS Method and CMR Method for Delay Differential Equations Associated with Semisimple Singularity[J]. International Journal of Bifurcation and Chaos， 2014，24（1）：1450003.

[19]NAYFEH A H. Order Reduction of Retarded Nonlinear Systems-the Method of Multiple Scales versus Center-manifold Reduction[J]. Nonlinear Dynamics， 2008（51）： 483-500.

[20]DAS S L， CHATTERJEE A. Second Order Multiple Scales for Oscillators with Large Delay[J]. Nonlinear Dynamics， 2005，39（4）：375-394.

（編辑：温泽宇）