基于博弈论的无线Mesh网络路由与信道分配联合优化算法
张维维,何家峰,高国旺,任丽莉,申铉京
(1.吉林大学 计算机科学与技术学院,长春 130012;2.长春师范大学 国际交流学院,长春 130032;3.31693部队,哈尔滨150036;4.西安石油大学 电子工程学院,西安 710065;5.长春师范大学 网络中心,长春 130032)
0 引 言
无线Mesh网(Wireless Mesh networks,WMN)结合了无线局域网(Wireless LAN,WLAN)和无线移动自组织网络(Ad-hoc网络)的优点,是针对特定业务需求而出现的一种新型无线网络技术[1]。其应用包括了家庭宽带网络(Home network)、区域和城网络(WMAN)、公共紧急通信、战场通信等[2]。由于具有传输速率高、架设方便、覆盖范围灵活以及较强的容错能力等优点,无线Mesh网络被认为是自组织无线网和自动可配置无线网中最有发展潜力的组网技术之一[3]。
由美国麻省理工学院成立的较早启动的WMN实验研究项目的实验数据表明,对于超过4跳的路径,基于TCP协议的端到端吞吐量在达到47.3 kB/s时,其端到端延迟为43 ms[4]。德国柏林洪德宝大学(HumboldtUniversity)的计算机科学学院的学生志愿者组建了名为Berlin Roof Net的WMN测试环境(Duarte et al. 2012)[5]。国内也对WMN进行了研究,比如天津技术开发区已采用无线Mesh解决方案在全区范围内进行部署,日后将实现达到200个监控点的分布式网络[6]。
著名科学家von Neuma和Morgenstern于20世纪中期提出了博弈论(也被称为对策论或赛局理论),主要研究某一博弈中决策者根据实时或者非实时的环境变化做出的决策对于最终收益的影响[7]。博弈论自出现之日起就在经济学领域得到了广泛应用,据统计,研究博弈论的学者们自博弈论诞生到2015年期间已经获得了8次诺贝尔经济学奖,其中在2012年时,更是以当时的获奖者Lloyd Shapley的名字命名了著名的Shapley值,在2014年时,诺贝尔经济学奖颁奖委员会将奖项颁发给了著有《博弈论》一书的法国作家——Jean Tirole[8]。
本文提出了一种新的基于博弈论的合作算法来解决联合路由与信道分配的最优化问题。提出了两个博弈策略:极大极小策略给所有节点分配最优极大极小路径,提供给纳什均衡策略一个常数向量;纳什均衡策略应用向量l计算最优发射功率来达到均衡的信道分配。纳什均衡点如果存在,解是唯一的。最后,通过数值仿真验证了联合簇间公平路由与信道分配算法的性能。
1 相关工作
在无线Mesh网络中,如果节点被允许绝对自私地管理,节点在低质量链路上可能选择转发包(因此发生一个更低的机会花销),而不是占据一种合作形式,在合作形式下节点转发通信在一条高质量链路上,在合作形式下可能得到公平的链接[8]。处理过程如下:假定每个资源节点(或是自私的或是合作的)是理性的。如果节点知道权力低将会受到网络的惩罚,一个自私节点不会所有时间在一个低质量链路上转发数据[9]。在另一方面,需要目标节点(收到流量)监测服务水平检测到部分源节点坏的行为,监测对硬件和软件都是一种需要很大能量花销的活动。因此,源节点考虑范围内合作而不是自私,与此同时,目标节点考虑监测来自于源节点的服务范围[10]。用贝叶斯博弈理论找到Nash均衡点确保源节点的最优合作范围和目的节点的最优监测率。本文的博弈理论公式是基于价格模型,为了确保可靠的链接,每个目标节点收益一定量的“虚拟货币”给源节点(基于预算)[11]。虚拟货币被执行作为可用网络经济的有限的令牌集合。源节点用货币购买链接目的节点的链接。假定源节点通过指令通信控制中间节点。

信道对竞争和节点自身之间的信道分配方案影响越来越大,是导致无线网络性能下降的最主要原因之一。虽然无线网络中的所有节点都设置有多个射频通信接口,但只有当连接的接口和信道保持通信时,每个接口才对应不同的信道。
为了适合节点自私自利的特性,几个新的基于博弈论的机制被设计在Mesh传感器网络的路由算法中。带有参数(V,T)的重复博弈方案被解释如下:每一个节点的效用U与阈值V比较。如果U 博弈论广泛应用于经济学领域,从最初的经济学领域建模发展到网络问题,用于仿真自私节点的合作。每个循环的进程从汇聚节点或基站重新调度基于最高的能量级别簇头,以应答信息到新的簇头的方式。该方法是基于实用动态源路由协议。协议的另一个重要方法是收益计算的阈值,阈值是0或者1。0代表取决于阈值的收益缩减,1代表取决于阈值的收益增加。与之前的Leach协议比较,基于阈值条件下收益用于发送能量数据,避免整个网络中的自大化攻击者。博弈论是簇间能效优化的网络性能优化方法。 解决相邻信道传输之间的干扰引起的约束问题,利用联合信道分配和路由器接口分配,将该问题看作是一种跨层网络效用最大化问题。在一个多信道无线Mesh网络中,两个逻辑链路(m,n),(m,p)∈L被定义为相互干扰,必须同时满足如下条件: (2)一个信道的发送/接收接口是在其他信道的发送/接收接口的干涉范围内。 通过建模,博弈了理论有效的改善路由协议性能。两个参与者的初始状态是最小化参与者和最大化参与者。定义博弈的每一个参与者和收益函数,量化最小参与者的结果;最小化参与者选择最小化函数,最大化参与者选择最大化函数。在使用博弈模型中,两个参与者是同样的。所有的路由器聚集到一起形成一个参与者,是路由器参与者的集合;另一个参与者是链路的集合,是网络参与者。路由器参与者集合的博弈移动是执行路由协议。网络参与者博弈移动是改变网络拓扑。极大极小策略搜索博弈树找到极大极小路径;极大极小值(极大极小结果)是应用到路径上的代价函数。极大极小值是在博弈的约束内,如果路由器已经被优化,那么,在网络内无论发生什么,路由器确保不会低于极小极大值。 不可转移收益合作博弈模型包括4个基本要素:局中人、结果集合、特征函数、以及收益函数。其中,局中人(参与者)是博弈过程中的决策主体,结果集是X,将N的每个非空子集S(即一合作)赋一个集合V(S) ⊆X的特征函数V。收益函数是局中人从各种策略中能够获取的收益。其中,N={1,2,…,n}为全部博弈局中人的集合,S=S1×S2×…×Sn为所有参与者的策略的集合,×为笛卡尔乘积。参与者i的收益是一个测量函数,用ui来表示。U表示所有局中人获得的收益集合,其中U={u1,u2,…,un}。不可转移收益模型是一种静态的博弈模型,在这个模型中,一些参与者合作达到高的收益率。本文采用极大极小合作纳什均衡,目标是最大化通信线路的收益,分析极大极小合作纳什均衡的存在,证明极大极小合作纳什均衡的必要条件。仿真结果显示,根据合作收益得到的多跳链路数据速率,极大极小合作纳什均衡优于合作纳什均衡方案和纳什均衡方案。 联合簇间公平路由与信道分配对随机博弈网络定义如下: SGN= (N,T,P,F,π,λ,R,U,M0) 每个参与者采用一个统一的随机分布策略,比如以0.5 的概率选择一个信道将本文采用的信道分配与随机分配信道相比较,5个参与者的节点的满意度明显高于随机分配。 剩余能量越小,成为簇头的概率越小: (1) 式中:fi为节点i当前的剩余能量,取值范围为[0,1];Ei为节点i在初始状态时所具有的能量;Ei0为剩余能量因子。 令簇头间的距离为最佳距离,就可以使得周围节点密度较大的节点更有可能成为簇头节点。 Leach协议不考虑节点是否曾经担任过簇头,对节点的任务分配极为不公平。对比分析节点的状态函数,增加节点的节点需求带宽等参数,构建节点的状态描述模型:定义ci,j为节点i在某一时刻j的贡献值衡量函数,Δc为不同的贡献变化值,而如何选择最终的簇头节点,就需要通过博弈论来解决问题。 (2) (3) 式中:b∈(0,1]为Ui函数中可调的参数,表示节点的带宽需求的满意程度,Ui为效用函数;Lw为节点在带宽w下传输数据帧(不包含控制信息)的长度为L;节点i在发送功率p下传输数据帧的长度为M;0≤s1≤s2≤…≤s,Si={0,s1,s2,…,s}为参与者i的策略空间。 对于任何两个节点m,n∈N,存在一条逻辑链路(m,n)∈L,定义一个C×1的信道分配向量Xmn,如果节点m与n在第i条频道进行通信,那么向量Xmn中的第i个元素就被设置为1;否则,将被设置为0。例如,假设C=5,节点m与n在第2条频道上进行通信,则Xmn=[0 1 0 0 0]T。 为了建立逻辑链路(m,n)∈L,路由器节点m与n应该分配通用的信道,即: Xmn=Xnm,∀m,n∈N, (m,n)∈L (4) lTXmn=1,∀m,n∈N, (m,n)∈L (5) 式中:l表示一个C×1的信道分配向量,其所有的向量元素均为1。考虑两个逻辑链路(m,n),(m,p)∈L,有如下公式: (6) 对于任何两个节点m,n∈N,存在一条逻辑链路(m,n)∈L,定义一个I×1的接口分配向量Ymn,如果节点m的第i个接口与节点n进行通信,那么向量Ymn中的第i个元素就被设置为1;否则,将被设置为0。例如,假设I=3,节点m使用其第1个接口与节点n进行通信,则Ymn=[1 0 0]T。 为了建立逻辑链路(m,n)∈L,路由器节点m与n应该使用它们的一个接口。需要特别注意的是,Ymn≠Ynm。然而,其仍然需要满足: lTYmn=1,∀m,n∈N,(m,n)∈L (7) (8) ∀m,n,p∈N;(m,n),(m,p)∈L 信道和接口联合分配模型可以表示为〈X,Y〉,在模型由信道分配向量Xmn和接口分配向量Ymn共同决定了所有逻辑链路(m,n)∈L的分配。 为Mesh传感器网络构造收益函数,通过并行迭代的方式获得网络信道分配的纳什均衡策略,使所有节点的收益函数达到最优化,节点i的收益函数Ui=M是节点i占用带宽进行直接传输所获得的吞吐量与节点i所获得的吞吐量之和除以节点i对所占用的协作带宽wi的支付。 对于联合合作博弈的模型,由于寻求模型(3)最优解的问题是一个NP难题,本文尝试用贪婪算法寻求近似最优解。 贪婪算法:设I表示当前带宽需求低的节点(参与者)构成的集合,若当前最大收益为Ui(j)=maxk∈N,l∈jrl(k)则说明参与者i的带宽需求高,则将参与者i放入表示带宽需求高的节点构成的集合j。 每个Mesh节点根据策略Si来选择效用Us,如果效用函数提高,则博弈过程再次进入循环。同时所有节点依次进行次操作从而达到纳什均衡。本文博弈基本算法步骤如下: (1)初始化,为N个Mesh节点分配信道,所有节点的策略组合记为S0。 (2)迭代过程,节点按照接入网络的顺序依次进行博弈,依次选择使得效用函数最大的策略,更新所有节点的策略组合为S*。 (3)终止过程,重复迭代过程,直至算法收敛。 在前文提出的基于不可转移收益合作博弈的簇间公平性路由联合信道分配的基础上进行仿真实验,使用仿真工具NS3作为仿真平台,验证路由协议的有效性,并对比簇间公平路由、所有Leach路由的吞吐量,对比不同的信道分配策略。设定边长为800 m的方形监测区域内,随机放置100个点。假设仿真场景中的无线路由器也是固定不动的,整个仿真网络参数设置如表1所示。为了方便计算,路由度量参数设定为跳数。算法求解合作博弈函数的最大值。 表1 仿真参数Table 1 Simulation parameters 实验设定目的地址是由路由器随机选择的,随后通过发送数据分组不断扩展整个无线网络的大小,图1为基于两种不同路由协议网络总吞吐量的对比值。其中,网络吞吐量定义为从源节点发送的在正确的接收时间内目的节点接收到的数据总量。由图1可以发现,2种路由协议的网络吞吐量随着节点数目的增多而发生变化,可以发现簇间公平路由协议的网络吞吐量明显高于LEACH协议的网络吞吐量。 图2中显示的是在9个节点的情景中对使用2种不同路由协议的无线路由网络中每个节点的吞吐量进行对比的结果。在这9个节点中,将第5个节点配置为网关节点,将第7个节点配置为与网关节点相距最远的节点。每个节点的吞吐量差别在簇间公平路由协议下基本保持相近的状态。这就说明簇间公平路由协议对于各个节点的公平性考虑得比较全面,每个节点通过簇间公平路由协议都可以得到相应的带宽,其公平性原则在分配带宽时显得尤为重要。 图2 节点的吞吐量对比Fig.2 Comparing nodes throughput 如图3所示,在节点(参与者)带宽需求相同时,比较基于博弈论的算法和基于贪婪算法的系统吞吐量,在参与者的平均带宽需求大于56 Mbit/s时,存在相互干扰,从而导致网络的吞吐量呈下降趋势,基于博弈算法的吞吐量明显大于基于贪婪算法的吞吐量。 图3 系统吞吐量与节点平均带宽需求之间的关系Fig. 3 Relationship of participants’ average business requirements and system throughput 本文根据无线Mesh网络中路由器分布的公平性原则,使用博弈论方法进行分析后将协议进行了路由协议。实验结果表明,基于博弈论的无线Mesh网络路由协议增加了网络吞吐量,并使得网络中各个无线节点占有的信道资源基本相近,满足公平性原则。这些研究可以很好地解决当前Mesh网络接入协议的问题,为Mesh网络的普及和应用提供非常重要的作用。 参考文献: [1]丛犁,张海林,刘毅,等.基于粒子群优化的协作网络资源分配的博弈策略[J].吉林大学学报:工学版, 2012, 42(1): 207-212. Cong Li,Zhang Hai-lin, Liu Yi,et al.Particle swarm optimized game theory for resource allocation in cooperative networks[J].Journal of Jilin University(Engineering and Technology Edition),2012,42(1):207-212. [2]鲁智,顾学迈,李世忠,等.新的速率与功率联合博弈的分布式控制算法[J].吉林大学学报:工学版, 2008, 38(2): 231-235. Lu Zhi,Gu Xue-mai, Li Shi-zhong,et al.Novel distributed rate and power on control algorithm based on joint game theoretic approach [J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(2): 231-235. [3]Duarte P B F, Fadlullah Z M, Vasilakos A V, et al. On the partially overlapped channel assignment on wireless mesh network backbone: a game theoretic approach[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(1): 119-127. [4]Gabale V,Raman B,Dutta P,et al.A classification framework for scheduling algorithms in wireless Mesh networks[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 199-222. [5]Vural S, Wei D, Moessner K. Survey of experimental evaluation studies for wireless Mesh network deployments in urban areas towards ubiquitous internet[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 223-239. [6]Jahanshahi M, Dehghan M, Meybodi M R. LAMR: learning automata based multicast routing protocol for multi-channel multi-radio wireless Mesh networks[J]. Applied Intelligence, 2013, 38(1): 58-77. [7]Chen J, He K, Du R, et al. Dominating set and network coding-based routing in wireless Mesh networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(2): 423-433. [8]Zhang Z, Long K, Wang J. Self-organization paradigms and optimization approaches for cognitive radio technologies: a survey[J]. IEEE Wireless Communications, 2013, 20(2): 36-42. [9]Wang B, Liu K J. Advances in cognitive radio networks: asurvey[J].IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1):5-23. [10]Kaabi F, Ghannay S, Filali F. Channel allocation and routing in wireless Mesh networks: a survey and qualitative comparison between schemes[J]. International Journal of Wireless and Mobile Network, 2010, 2(1): 132-151. [11]de Domenico A, Strinati E C, di Benedetto M G. A survey on MAC strategies for cognitive radio networks[J].Communications Surveys & Tutorials,2012, 14(1): 21-44. [12]Rezgui J, Hafid A,Gendreau M. Distributed admission control in wireless mesh networks:models,algorithms,and evaluation[J].IEEE Transactions on Vehicular Technology,2010,59(3):1459-1473.2 吞吐量分析及模型构建
2.1 预备知识
2.2 不可转移收益合作博弈方法
2.3 基于合作博弈的联合簇间公平路由与信道分配模型

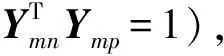
3 仿真和性能分析



4 结束语

