基于有限序列的压缩新算法
赵宏伟,刘宇琦,特日根,陈长征,臧雪柏,3
(1.吉林大学 计算机科学与技术学院,长春 130012;2.中国科学院 应用光学国家重点实验室,长春 130033; 3.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012;4.长光卫星技术有限公司,长春 130000)
0 引 言
数据业务和多媒体通信业务等通信量越来越大,给信息存储特别是网络传输带来前所未有的压力。现有数据压缩算法分为无损压缩和有损压缩。有损压缩通过数据挖掘等手段从数据来源、数据特性出发,提取关键信息予以保存。语音识别、市场销售数据、气象数据、电信通信数据等均可采用有损压缩方法处理。针对这种数据的有损压缩通常有两类办法[1]:数据汇聚和数据近似。汇聚函数以抛弃数据中的原始结构为代价,减少数据量,但这种方法使得一些有用的知识被删除,其中主要包括COUNT、SUM、AVG等方法;数据近似[2]可视为基于模型的数据获取,通过对采集到的感知数据进行分布式建模,可减少数据传输量、节省网络能量、延长网络生命。有损压缩方法可分为基于概率模型[3]、基于时间序列分析模型[4]、基于数据挖掘模型[5]、基于数据压缩模型[6]4类,其共性在于压缩率高,数据还原质量依赖于算法实现的代价。
无损压缩技术[7]在数据压缩过程中不允许损失精度,可以保真还原。主要用于文本文件、数据库、程序数据和特殊应用场合的图像数据(如指纹图像、医学图像)等压缩。游程长度编码[8]通过去除文本中的冗余字符或字节中的冗余位,达到减少数据文件所占的存储空间的目的,其压缩效能取决于整个数据流的重复字符出现次数、平均游程长度以及所采用的编码结构。由于该算法是针对文件的某些特点所设计的,具有一定的局限性。Gödel[9]提出一种不依赖于数据库的无损压缩方法,称为哥德尔数方法,但其使用范围局限于对图灵机程序的压缩,因此不具有普遍性。
本文提出了CSNB(Compress sequence number-Binary)压缩算法,通过增加校验位的形式实现压缩。
1 压缩排序数
1.1 CSNB
定义1 对于任意序列,其对应的最小字长的二进制序列为原序列的CSNB序列。
例:若序列为1,3,2,6,5,4,则CSNB序列为001,011,010,110,101,100。
定义2 任意1到n的全排列序列,通过式(1)计算得到的二进制数为此序列的奇偶校验码CSNBc:
⊕
(1)
式中:N⊕表示在二进制数N中每位依次求异或所得到的值;CSNBi为CSNB序列中的第i个数。
例:若序列为1,3,2,6,5,4,CSNB序列为001,011,010,110,101,100,则奇偶校验码的计算过程为:
001⊕=1;011⊕=0;010⊕=1;
110⊕=0;101⊕=0;100⊕=1
CSNBc为100101。
定义3 任意CSNB序列,通过式(2)计算所得的值为CSNB序列的前序错位求和部分CSNF。
(2)
定义4 任意CSNB序列,通过式(3)计算所得的值为CSNB序列的后序错位求和部分CSNA。
(3)

定义5 任意CSNB序列,通过式(4)计算所得的值为CSNB序列的CSNB。

10n×CSNA+CSNBc
(4)
因为CSNB序列为二进制序列,所以式(4)为二进制计算。
例:CSNB序列为:001,011,010,110,101,100

10n×CSNA+CSNBc=101111×
(100×1+101×11+1010×10+
1011×110+10100×101+10101×100)+
10110×(100×100+101×101+1010×110+
1011×10+10100×11+10101×1)+
100101=10000111110000110100101
1.2 CSNB与原序列的比较
原序列以十进制的方式记录排序序列。计算机对十进制数常用的编码方式是BCD码,以16位计算机为例,在记录十进制数时计算机会为每个十进制数预留16位。而CSNB序列是以二进制的方式记录排序序列,计算机在记录时不需要编码转换。其对比结果如表1所示。
原序列、CSNB序列以及CSNB都具有记录序列的功能,其空间复杂度对比结果如表2所示(计算机为k位)。

表1 原序列与CSNB序列的比较Table 1 Comparison of original sequence and sequence CSNB

表2 CSN序列、CSNB序列以及CSNB占用空间对比Table 2 CSN sequence,CSNB sequence and CSNB space comparison bit
由表2可知,当序列长度n≤8时,CSNB序列较CSNB有更好的空间利用率,且CSNB序列并没有进行改装压缩,所以也不需要繁琐的解压过程,但当8 定义6 如果一个节点N的奇偶校验码为N⊕1,其祖先节点要求的奇偶校验码为1,且N⊕1≠1,则剪枝发生在该节点之上,此时,称该剪枝过程为奇剪枝。 定义7 如果一个节点N的奇偶校验码为N⊕1,其祖先节点要求的奇偶校验码为0,且N⊕1≠0,则剪枝发生在该节点之上,此时,称该剪枝过程为偶剪枝。 定义8 如果一个在第n层(根节点为第0层)的节点N与回溯到根节点中所有遍历到的节点进行式(3)的计算,得到结果的倒数第n位为C,其祖先节点要求的01校验码为1,且C≠1,则剪枝发生在该节点之上,此时,称该剪枝过程为1剪枝。 定义9 如果一个在第n层(根节点为第0层)的节点N与回溯到根节点中所有遍历到的节点进行式(3)的计算,得到结果的倒数第n位为C,其祖先节点要求的01校验码为0,且C≠0,则剪枝发生在该节点之上,此时,称该剪枝过程为0剪枝。 性质1 由于奇偶剪枝不需要累加运算,且在选定下一节点时可直接计算,并且奇偶剪枝针对的是真实的排序值,所以奇偶剪枝较01剪枝速度更快、效率更高。 虽然通过决策树的剪枝方法能够删掉大多数非解节点,但剪枝后的决策树仍然可能存在多个所在层为n的叶子节点,所以还需要通过CSNA对所有可能解进行检验。 例:CSNB序列为:001,011,010,110,101,100,CSNB=100001111100101,其剪枝策略如图1所示,先进行奇偶校验,再进行01校验。其中,“奇×”、“偶×”、“1×”和“0×”分别表示进行奇剪枝、偶剪枝、1剪枝和0剪枝操作。 图1 剪枝策略示意图Fig.1 Pruning strategy schematic 创建决策树是从逻辑的角度分析算法的执行过程,本质上解压算法并不需要构建决策树。决策树在选择节点时,是通过剪枝策略来判断其选择的节点是否正确,从逻辑角度来说,是尝试着确定CSNBi的位置。 根据式(2)求CSNBi,本质上是在求以CSNB1,CSNB2,…,CSNBn为未知数,方程CSNF=20×CSNB1+21×CSNB2+…+2n-1×CSNBn(方程为十进制方程)的解,其中当i≠j时,CSNi≠CSNj且1≤CSNi≤n。 而决策树是在明确CSNBi值的情况下,去求其位置,即为求以x1,x2,…,xn为未知数,方程CSNF=2x1×CSNB1+2x2×CSNB2+…+2xn×CSNBn(方程为十进制)的解,其中当i≠j时,xi≠xj且1≤xi≤n-1。 根据以上分析,可制定CSNB解压算法的步骤如下所示。 (1)建立记录所有未知数状态的未知数状态表(Statetable),所有未知数的初始状态是Uncertain。若未知数个数为n,则未知数的其他可能状态数为[1,n]中的整数。 (2)从Statetable中提取一个未被测试过的且状态为Uncertain的未知数,并执行第(3)步。如果不存在符合条件的未知数,则执行第(5)步。 (3)将选定的未知数依次通过奇偶检验和01检验,如果都通过,则执行第(4)步;否则,将此未知数视为已检测状态,并执行第(2)步。 (4)将选定的未知数的初始状态更改为未被选定的状态中最小的状态数,将其他状态为Uncertain的未知数均视为未被测试状态,执行第(2)步。 (5)若Statetable中仍存在状态为Uncertain的未知数,则将状态数最大的未知数以及之后的未知数状态设定为Uncertain,将之后的未知数视为未检测状态,并继续执行第(2)步;否则执行第(6)步。 (6)通过CSNA判断找到的可能解的正确性,若正确,算法结束;否则,将状态数最大的未知数以及之后的未知数状态设定为Uncertain,将之后的未知数视为未检测状态,并执行第(2)步。 所谓正向检验,就是给定任意排列的CSNB,由CSNB解其原序列,若解唯一,不仅能说明CSNB系统的正确性,还能检验解压算法的正确性。 任意长度为n的CSNB序列,其全排列的总数为n!,当n=9时,一共有9!=362880种排列情况,一一测试是不合理的,所以当1 表3 正向检验解的唯一性Table 3 Positive test uniqueness of the solution 由表3可知,CSNA的查错率更高。假设没有奇偶校验和没有CSNA校验的多解率符合某种概率分布,且是相互独立的,则当5 所谓反向检验,就是给定任意排列的CSNB,计算是否存在一个不同的CSNB序列的CSNB与其相同,若存在则解不唯一;若不存在则解唯一。通过对比正向检验和反向检验的结果可知解压算法的正确性。 任意长度为n的CSNB序列,其全排列的总数为n!,通过与其所有不同的CSNB序列作对比,其比较次数为n!!。当n=9时,一共有9!!=362880!次比较,这样测试是不合理的,所以采用与正向检验相同的方法对其进行反向检验,即当1 表4 反向检验解的唯一性Table 4 Uniqueness of the solution of reverse test 研究了排序序列的记录及存储方式,提出了CSNB的存储方式,CSNB中包含有前序错位求和CSNF、后序错位求和CSNA以及奇偶校验码3部分。CSNB通过对排序序列进行压缩,其空间复杂度为O(log2n+n)。通过解压算法可找到对应的原序列,实现序列还原。CSNB的压缩不仅可以使其具有更好的空间利用率,而且能够增加信息传递的可靠性。 参考文献: [1] Deligiannakis A,Kotidis Y,Roussopoulos N. Dissemination of compressed historical information in sensor networks[J]. The VLDB Journal,2007,16(4):439-461. [2] 张建明,林亚平,周四望,等. 传感器网络中误差有界的小波数据压缩算法[J]. 软件学报,2010,21(6):1364-1377. Zhang Jian-ming,Lin Ya-ping,Zhou Si-wang,et al. Haar wavelet data compression algorithm with error bound for wireless sensor networks[J]. Journal of Software,2010,21(6):1364-1377. [3] Chu D,Deshpande A,Hellerstein J M,et al. Approximate data collection in sensor networks using probabilistic models[C]∥Proceedings of the 22nd International Conference on Data Engineering,Atlanta,USA,2006:48-59. [4] Najafi H,Lahouti F,Shiva M. AR modeling for temporal extension of correlated sensor network data[C]∥International Conference on Software in Telecommunications and Computer Networks,Split, Croatia,2006:117-120. [5] Borgne Y L,Bontempi G. Unsupervised and supervised compression with principal component analysis in wireless sensor networks[C]∥13th ACM International Conference on Knowledge Discovery and Data Mining,New York,USA,2007:94-103. [6] Ganesan D,Estrin D,Heidemann J. DIMENSIONS:Why do we need a new data handling architecture for sensor networks?[J]. ACM SIGCOMM Computer Communication Review,2003,33(1):143-148. [7] 郑翠芳. 几种常用无损数据压缩算法研究[J]. 计算机技术与发展,2011,21(9):73-76. Zheng Cui-fang. Research of several common lossless data compression algorithms[J]. Computer Technology and Development,2011,21(9):73-76. [8] Tsang P,Liu J P,Cheung K. Modern methods for fast generation of digital holograms[J]. 3D Research,2010,1(2):11-18. [9] Gödel K. Über formal unentscheidbare Sätze der Principia Mathematica und Verwandter Systeme I[J]. Mathematics and Statistics,1931,38(1):173-198.2 CSNB解压
2.1 创建决策树


2.2 CSNB解压算法
3 系统测试及结果分析
3.1 解的唯一性正向检验
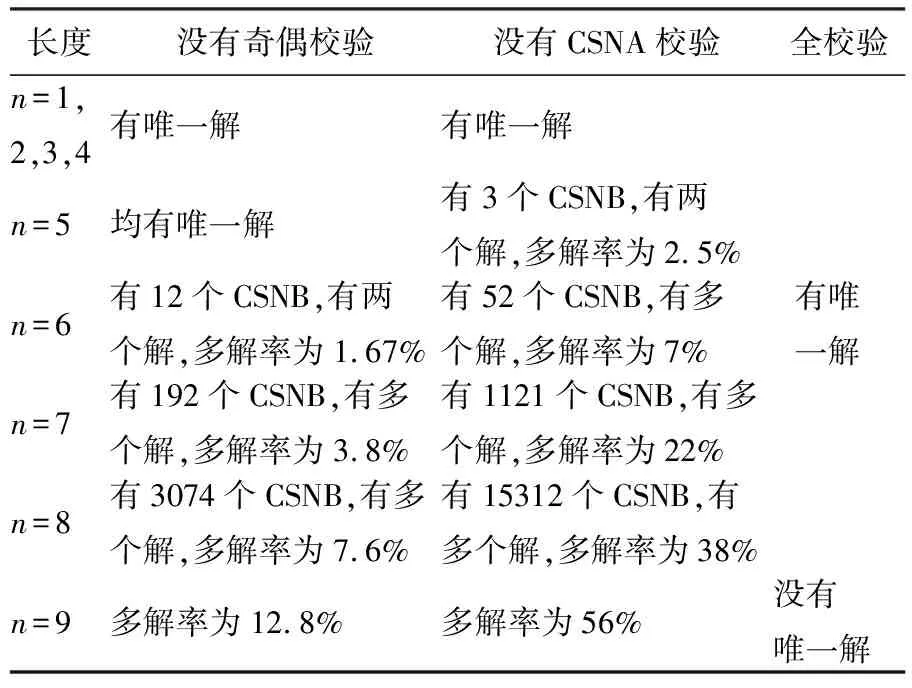
3.2 解的唯一性反向检验

4 结束语

