基于模糊补偿的RBF神经网络机械手控制

毛 润, 高宏力, 宋兴国

(西南交通大学机械工程学院, 四川 成都 610031)

机械手学科是一门迅速发展的综合性前沿学科,广泛应用于工业生产系统中的各个环节,由于其结构本身具有高度非线性、强耦合性,同时模型本身具有不确定性和时变性,受到工业界和学术界的高度重视[1-2].近些年,机械手高性能控制算法一直是研究热点.目前,工业机器人使用最广泛的控制方法是比例微分(proportion differentiation, PD)控制,但实践表明,线性PD控制往往使驱动机构有很大的初始力矩,且机械臂本身所承受的最大力矩也是有限的,这将使通过增大PD系数来进一步提高系统性能受到限制[3-4].当控制系统受到极小的扰动,PD控制基本能够满足系统的精确度要求.但实际系统往往受到扰动、参数不确定等因素影响,因此对系统的鲁棒性提出很高的要求.逆运动学方法也是机器人控制系统最常用到的方法之一[2].逆运动学方法需要模型的先验知识,但是实际系统包含摩擦和未建模部分等很多不确定因素,所以机械手很难被精确建模.，黄晓蓉等[5]提出运用LS_SVM 对齿轮传动系统未建模部分进行逼近，但运用在高度非线性机械手系统中存在收敛速度不理想的问题.还有很多学者提出了利用神经网络补偿系统的扰动和未建模部分[6-11].神经网络控制方法不需要系统的数学模型,并且能够逼近任意非线性函数,使得它在非线性系统控制中得到广泛应用.但是单纯运用神经网络对机器人系统进行整体逼近,系统会遇到过拟合和学习时间过长的问题.还有很多学者运用模糊系统万能逼近理论进行机械手轨迹跟踪控制,旨在解决传统控制方法难于建模和系统未知扰动[12-15].综合对比可知常规控制很难实现快速高精度的跟踪控制,而传统的模糊控制对较强的非线性干扰控制效果较差.于是很多学者相继提出了误差补偿、时滞补偿、摩擦补偿等多种补偿控制策略[16],但是单一补偿策略并不能同时获得高精度的跟踪效果和消除非线性干扰.

本文结合文献[17-18],提出一种基于神经网络建模和模糊补偿的PD控制方法.该控制器由径向基(radial basis function, RBF)神经网络(neural network, NN)和模糊补偿器两部分构成.PD控制器的目的是获取机械手关节的速度、角速度和角加速度数据,将这些数据用作RBF神经网络的训练得到机械手的模型参数,并利用模糊补偿器对未建模部分和扰动进行自适应补偿.该控制方法的优点是能够在不知道系统模型的情况下辨识出模型,并具有较高的控制精度.

1 机械手系统动力学方程

根据Lagrangian方程,N关节机械手动力学方程表示为

τ+τd=

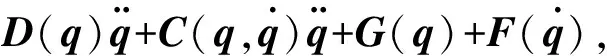
(1)

式中:τ为控制输入；

当模型被精确建立,且τd=0时,有

q∈Rn为关节角位移量;

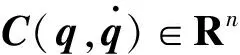
G(q)∈Rn为重力项;

机械手动力学模型有以下几个特性[19-20]:

(1)D(q)为一个正定对称矩阵,且是有界的,即存在已知正常数m1和m2,使得

m1I≤D(q)≤m2I;

（1）布置适量且有梯度的课后练习。布置作业时控制好数量和难度，既能满足学生需求并具有难度，激发学生对新知识的渴望，从而去主动发现学习新知识。

成立;

(4) 未知扰动满足τd≤τM,其中，τM为一个已知正常数.

2 逆动力学控制

步骤3求取目标值与实际输出的偏差e;

进入3月份以后，气温逐渐回升，此时应加强肥水管理，促进果实快速膨大，喷施磷酸二氢钾300倍液，7～10天1次，喷7～8次，每隔10天浇1次肥水，一直管理到采收结束。

(2)

为了书写方便将式(1)表示为

经人工重砂，光薄片的观察，矿石成分主要为磷灰石、石英、碳酸盐(以方解石为主)，其次为赤铁矿，磁铁矿，钛铁矿，褐铁矿、长石，微量矿物有锡石、黄铁矿、云母、辉石、闪石、绿帘石。

在课堂教学中，教师只有把学生的学习情绪调动起来，才能构建良好的课堂气氛，才能使学生在认知的过程中产生愉悦感，并激起和发展他们的智力。现代教育理论认为，只有良好的教学策略，才能达到良好的教学效果。而如何调动学生的学习情绪，对教师而言，是具有艺术性的教学策略。

(3)

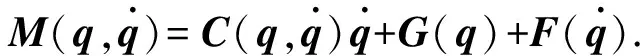
(4)

将输入控制向量τ表示为

τ+τd=τp+τs,

在考核内容上注重质量，增设“学生”维度，为其提供话语权，增强课堂参与程度，与教师共同就“观点内容”、“呈现方式”、“表达能力”、“时间控制”以及“过程组织”5方面进行多角度审视。在考核方式上涉及“组内评价”、“组间互评”和“教师评价”，其中，“组内评价”要求各成员之间就成果贡献值进行评价，实现组内监督作用，“组内互评”方式要求其他小组按照指定的评分标准给予现场打分，学生也由课堂旁观者变成了课堂参与者、主导者，而“教师评价”方式则重点进行查漏补缺与适当补充。

(5)

式中:τp为主控制器的输入,

(6)

τs为辅助控制器的输入,

(7)

式中：Kp和Kv为增益.

以直径25.4 mm、高5.0 mm的GH3536高温合金作为基体。先对其进行汽油除油和超声清洗，再喷砂粗化以增加表面活性，并提高涂层与基体间的机械咬合效率。喷砂材料为24号锆刚玉，喷砂压力为0.4 ～0.5 MPa，喷砂距离100 ～ 150 mm，喷涂至基体表面粗糙度Ra ＞ 3 μm。随后用压缩空气清除试样表面吸附的刚玉砂粒，获得干净、具有活性和易附着的表面状态。

τd为扰动，τd∈Rn；

D(qd)=D(q),

qd=q,

联立式(3)和式(5)得稳定的闭环系统为

(8)

(9)

式中:ΔD=D0-D;

ΔM=M0-M;

(10)

其中建模不精确部分

(11)

则式(10)可表示为

(12)

3 RBF神经网络名义模型学习

图1 基于RBF名义模型系统结构Fig.1 RBF-based structure of the proposed model

多输入单输出高斯径向基神经网络结构如图2所示,输入x=(x1,x2,…,xn)T,

(13)

式中:cj=(cj1,cj2,…,cjn)为第j个隐层神经元的中心点向量值；

b=(b1,b2,…,bj,…,bm)T,bj为隐层神经元j的高斯基函数的宽度.

周末的教室灯光昼亮，三三两两的同学正沉浸在书山题海中。沐子并不在教室，但我们座位下的纸箱已被她分门别类塞满了刚买好的各种零食。我选出一枚果冻，剥开放进嘴里，酸酸甜甜的味道，像青春九曲回环的委婉惆怅。

观察其不同检查方式的临床表现，并由2名影像科资深医师对本次检查所得资料进行阅览，若遇到意见不统一之处及时进行商讨确定，随后按照资料所显示详情对患者做出诊断，同时对其诊断准确率实施观察统计。

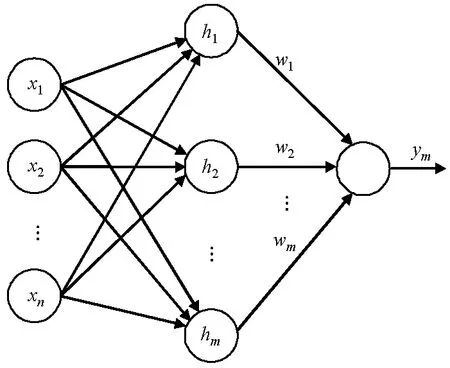
图2 RBF神经网络结构Fig.2 Structure of RBF neural networks

步骤2求取隐层、输出层各节点的输出;

在实施开展“坡地村镇”试点工作中，始终遵循以人为本，壮大村集体经济。比如山川村的赤豆洋高山生态旅游度假项目，农民的腰包在项目的建设过程中迅速鼓起来，预计每年为集体增收100余万元，带来就业岗位400余个，可为村民带来户均每年收入增加3万余元，农民收入可望实现持续快速增长。天子湖镇的余石安置项目，通过统一规划、整体推进，实行田、水、路、林、村全域综合整治，推行公共服务设施、绿化设施等全面配套，实现农民居住向中心村庄集中，有效提升了居住环境质量。

w=(w1,w2,…,wm)T,

则RBF网络的输出为

ym(t)=wT·h,

(14)

式中:h=(h1,h2,…,hm)T.

根据式(6),两关节机械手可表示为

(15)

式中:D1、D2为正定惯性矩阵D的两个列向量;M1、M2为M的两个列向量.

课后结合学习知识，以“怎样才能过一个健康的、充实的、快乐的周末”为例，要求学生制订休息日作息安排计划，在周末按照安排进行实践，并将感受写下来。学生通过切身体验发挥主观能动性，让自己的生活变得充实而有意义。

在实际控制中,通常机械手的实际模型不可知,利用4个RBF神经网络分别实现对D1、D2、M1和M2的逼近,输出为D10、D20、M10和M20,既能逼近未知系统模型,又能够补偿系统未知的摩擦特性[9].这样就产生了两关节机械手近似模型,其控制力矩表示为

(16)

运用MATLAB进行编程,算法如下:

开始:

步骤1初始化设置神经网络隐层节点数、基函数参数cD、cM和参数b、w,并给定输入向量和目标向量;

设网络的权值向量

文献的难度不尽相同，如果由教师指定阅读任务，公平性难以保证；随机抽取虽然公平，但难以发挥每组的特长。如果由教师指定某些知识点，然后由学生自主查找文献，这样既减轻了教师负担，也锻炼了学生的文献查找能力，同时也更为公平。文献的分配方式可以进一步探讨。

机械手的逆运动学是已知末端轨迹求解各个关节角度的过程.逆动力学控制也称为计算力矩方法,要求控制器已经获得模型的先验知识[18].对于机械手轨迹跟踪控制系统而言,控制目标包括各关节角度、角速度和角加速度.因此设理想角位移为qd,则跟踪误差为

步骤4若e满足要求,则训练完成;若e不满足,则求取隐层节点误差;

步骤5求取网络权值自适应律,并进行权值更新;

步骤6跳回步骤2.

结束.

4 模型不确定部分模糊补偿

在第2节中式(12)给出了基于逆运动学控制模型,但是这种控制方法鲁棒性较差.为了提高模型的鲁棒性,解决实际工况下的各种扰动和负载变化,给出了基于模糊补偿的控制系统结构,如图3所示.对比图1增加了一个模糊补偿器用于对系统的不确定因素进行补偿.

图3 基于模糊补偿控制系统结构Fig.3 System structure of the fuzzy compensator

一个多输入多输出(MIMO)模糊系统

“智慧珠”实验可简可难，千变万化，让学生乐在其中，多种的平面及立体的变化，可以持续不断地迎接挑战，带给学生持续的快乐和成就感。在实验过程中，学生判断事物的速度与能力提升了，其敏捷思维的能力加强了，高阶思维的火花在不断地碰撞、激发。当然，在结伴研究的过程中，学生合作的意识、组织协调能力也得到了锻炼，评价思维也有了历练。可以说，通过实验，学生的各项隐性认知都得到了发展。

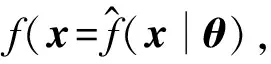
(17)

IFx1isA1,li… andxnisAn,ln,

这张不同寻常的地图是由萨普手绘的，数据由希森收集。（萨普作为一名女性，当时不允许她登上研究轮船。）地图显示，一条庞大的水下山脉呈南北向延伸，像一道巨大的接缝位于海洋的中部，这条山脉被称为大西洋中脊。萨普发现，这条山脉的中间有一道又深又阔的裂缝，裂缝的两边都是高高的山峰。她把这个作为证据来说明海洋地壳是运动的。她是正确的，这一点也支持了魏格纳被边缘化的大陆漂移理论。然而，萨普的同事希森赞成地球膨胀论，遗憾地将她的理论当作是“女孩讲的空话”。

运用乘积推理机、单值模糊器和中心平均解模糊器得

(18)

(19)

(20)

(21)

D(q)∈Rn×n为机器人的惯性力矩;

(22)

5 控制器设计与稳定性分析

取控制律

(23)

可表示为

τ=τ0+τf,

(24)

(25)

(26)

(27)

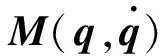
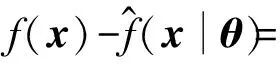
则式(27)可表示为

(28)

由于矩阵A特征根实部为负,则存在正定矩阵P和Q满足Lyapunov方程,

PA+ATP=-A.

(29)

定义Lyapunov函数

(30)

(31)

取自适应律为

(32)

则有

(33)

代入式(31)得

(34)

(35)

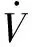
(36)

可见当Q的特征值越大,P的特征值越小,模糊补偿器误差上界ε0越小,则x的收敛半径越小,跟踪效果越好.因此用控制律式(24)能够保证闭环系统的稳定性.

6 MATLAB/Simulink仿真

选取两关节机器人系统分析和验证控制方法的有效性.如图4为两关节机械手结构示意图,其中：l1、m1、q1分别表示关节1的长度、质量和角位移；l2、m2、q2分别表示关节2的长度、质量和角位移；θ1、θ2分别表示关节1、2的角度；g表示重力加速度.

图4 两关节机械手结构示意Fig.4 Structure of two-link robot manipulators

其动力学模型为式(1),即

式中:

τd=[0.2sint0.2sint]T.

将ΔD=D0-D、ΔM=M0-M代入式(1),得

其中，f在式(11)中已经给出.

取p=[3.60 0.84 0.89 3.90 0.50]；

被控对象初值为

q0=[0.09 -0.09]T,

仿真中取两种位置指令,

q1,d=0.2+0.4(sint+sin 2t),

q2,d=0.4+0.2(cos 4t+0.2 cos 6t)；

取控制器参数为

Kp=150eye(2),

Kv=150eye(2),

Q=100eye(4).

神经网络隐含层选择1层,按照经验公式进行初选,再进行简单试验对比,该隐含层选取7个隐含节点.

基于计算速度和控制精度的考虑模,糊规则每一项折衷选择,分为5个模糊集构成集合A,

A={Aj|j=1,…,5}={NB,NS,O,PS,PB},

隶属度函数采用高斯型.

如图5、6、7分别为没有模糊补偿情况下关节1、2的轨迹跟踪曲线图和跟踪误差曲线图.对比增加了模糊补偿的情况,如图8、9、10,可以看出后者的控制精度明显优于前者.如图11、12、13所示,增加了模糊补偿的系统,关节1、2的加速度跟踪效果也表现优异,关节控制力矩曲线较为缓和,整体表现满足控制要求.

为了更加直观和精确地对比两个机械手轨迹跟踪控制系统表现效果,对系统跟踪误差的均方根误差(root mean square error, RMSE)进行测量计算.如表1所示,结果表明运用RBF神经网络进行名义模型学习后,增加了模糊补偿的轨迹跟踪效果表现明显优于没有模糊补偿的控制方法,其中两关节跟踪精度分别提高了60.8%和70.4%.

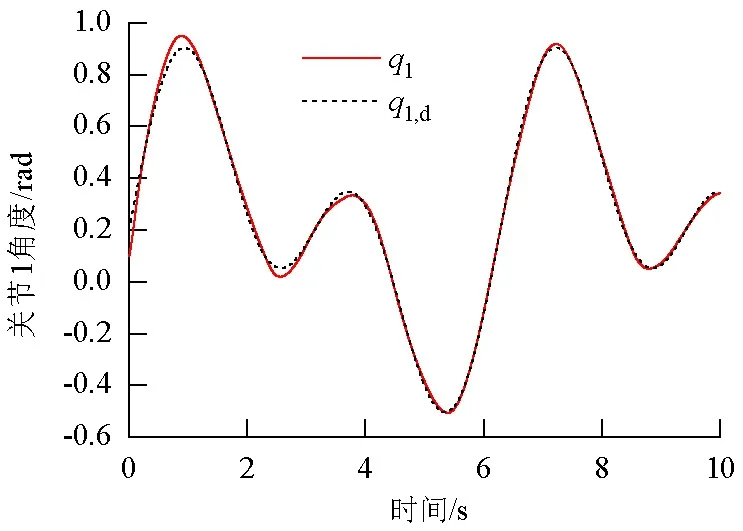
图5 无模糊补偿关节1轨迹跟踪Fig.5 Position tracking of the first joint without fuzzy compensator

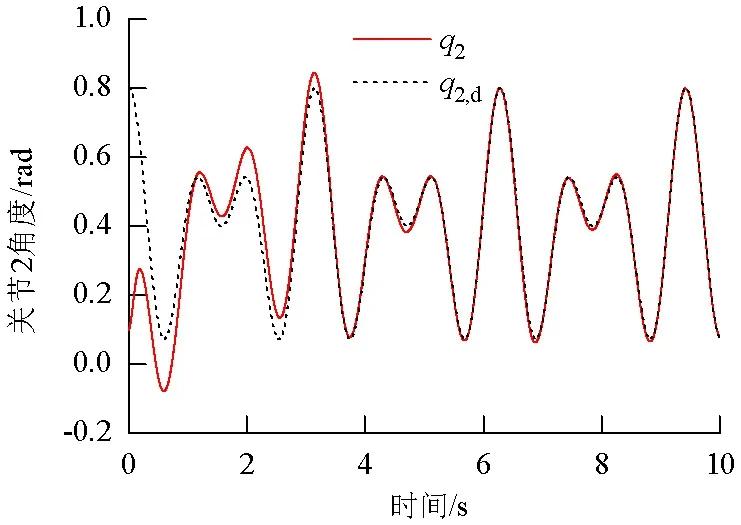
图6 无模糊补偿关节2轨迹跟踪Fig.6 Position tracking of the second joint without fuzzy compensator

图7 无模糊补偿两关节跟踪误差Fig.7 Position tracking errors of the two joints without fuzzy compensator

图8 无模糊补偿两关节控制力矩Fig.8 Control torques of the two joints without fuzzy compensator

图9 有模糊补偿关节1轨迹跟踪Fig.9 Position tracking of the first joint with fuzzy compensator

图10 有模糊补偿关节2轨迹跟踪Fig.10 Position tracking of the second joint with fuzzy compensator

图11 有模糊补偿两关节跟踪误差Fig.11 Position tracking errors of the two joints with fuzzy compensator

图12 有模糊补偿关节1角速度Fig.12 Angular velocity of the first joint with fuzzy compensator

图13 有模糊补偿关节2角速度Fig.13 Angular velocity of the second joint with fuzzy compensator

图14 有模糊补偿两关节控制力矩Fig.14 Control torques of the two joints with fuzzy compensator

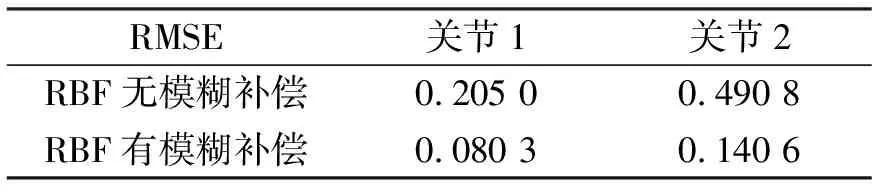
表1 两种控制方法误差RMSE对比Tab.1 Tracking errors represented by the RMSE for each joint using various control schemes

7 结束语

本文提出一种基于逆模型RBF神经网络名义模型学习和模糊补偿的控制策略,首先对机械手关节模型进行逆运动学分析,构造出计算力矩模型,再运用RBF神经网络对名义模型进行学习,最后增加模糊补偿器对系统未建模部分和扰动进行补偿.该方法不依赖于机械手复杂的数学模型,易于实现,最后仿真实验表明该方法取得很好的控制效果,对于工业机器人轨迹跟踪控制研究有一定的参考价值.

本文在理论上提供一种解决机械臂轨迹跟踪的方法,对于模型学习,模糊补偿带来的系统复杂度提高是否影响系统快速性问题尚未提供量化分析.工业应用中,既要考虑精度又要考虑效率,因此今后的研究中可以将此建立优化模型,针对不同的应用场景,提供最优控制方案.

[1] 蔡自兴. 机器人学[M]. 北京:清华大学出版社,2000: 3-4.

[2] CRAIG J J. Introduction to robotics: mechanics and control[M]. [S.l.]: Addison-Wesley Pub. Co, 1986: 95-98.

[3] 焦晓红,李运锋,方一鸣,等. 一种机器人鲁棒自适应控制法[J]. 机器人技术与应用,2002(3): 40-43.

JIAO Xiaohong, LI Yunfeng, FANG Yiming, et al. A robust adaptive control strategy of robotic manipulator[J]. Robot Technique and Application, 2002(3): 40-43.

[4] 陈启军,王月娟,陈辉堂. 基于PD控制的机器人轨迹跟踪性能研究与比较[J]. 控制与决策,2003(1): 53-57.

CHEN Qijun, WANG Yuejuan, CHEN Huitang. Comparative research of trajectory tracking performanceof robotic manipulator based on PD control scheme[J]. Control and Decision, 2003(1): 53-57.

[5] 王良勇,柴天佑. 带有神经网络补偿的机械手PD控制[J]. 中国电机工程学报,2009,29(12): 110-115.

WANG Liangyong, CAI Tianyou. Neural network compensator based PD control of robotic manipulator[J]. Proceedings of the CSEE, 2009, 29(12): 110-115.

[6] 王良勇,杨枭. 带有前馈和神经网络补偿的机械手系统轨迹跟踪控制[J]. 电机与控制学报,2013,17(8): 113-118.

WANG Liangyong, YANG Xiao.Trajectory tracking control for robotic manipulators endowed with feedforward and neural networks[J]. Electric Machines and Control, 2013, 17(8): 113-118.

[7] 关新平,唐英干,段广仁. 机械手臂基于神经网络动态补偿的自适应控制[J]. 控制理论与应用,2003(1): 101-104.

GUAN Xinping, TANG Yinggan, DUAN Guangren. Adaptive control for manipulator based on neural network dynamic compensation[J]. Control Theory & Applications, 2003(1): 101-104.

[8] WAI R J, CHEN P C. Robust neural fuzzy network control for robot manipulator including actuator dynamics[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1328-1349.

[9] FENG G. A compensating scheme for robot tracking based on neural networks[J]. Robotics & Autonomous Systems, 1995, 15(3): 199-206.

[10] KIM Y H, LEWIS F L. Neural network output feedback control of robot manipulators[J]. IEEE Transactions on Robotics & Automation, 1999, 15(2): 301-309.

[11] 董立红. 基于模糊补偿的机械手鲁棒自适应模糊控制研究[J]. 计算机工程与科学,2012,34(1): 169-173.

DONG Lihong. Research on the robust adaptive fuzzy control of manipulator based on fuzzy compensation[J]. Computer Engineering & Science, 2012, 34(1): 169-173.

[12] CHEN Y, MA G, LIN S, et al. Adaptive fuzzy computed torque control for robot manipulator with uncertain dynamics[J]. International Journal of Advanced Robotic Systems, 2012, 9(1): 142-170.

[13] YOO B K, HAM W C. Adaptive control of robot manipulator using fuzzy compensator[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(2): 186-199.

[14] SUN F C, SUN Z Q, FENG G. An adaptive fuzzy controller based on sliding mode for robot manipulators[J]. IEEE Transactions on Systems Man & Cybernetics Part B, 1999， 29(5): 661-667.

[15] HSU C F, CHENG K H, LEE T T. Robust wavelet-based adaptive neural controller design with a fuzzy compensator[J]. Neurocomputing, 2009, 73(1): 423-431.

[16] KIM D, HUH S H, SEO S J, et al. Self-organizing radial basis function network modeling for robot manipulator[C]∥18th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems: Innovations in Applied Artificial Intelligence. Bari: IEA/AIE, 2005: 579-587.

[17] ABDESSEMED F. Svm-based control system for a robot manipulator[J]. International Journal of Advanced Robotic Systems, 2012, 9(6): 247.

[18] 刘金琨. 智能控制[M]. 北京:电子工业出版社,2014: 92-93.

[19] 刘金琨.机器人控制系统的设计与MATLAB仿真[M]. 北京:清华大学出版社,2008: 35-36.