Hausdorff算子在Herz型空间上的加权估计*

廖嫒嫒， 吴小梅

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 金华 321004)

0 引 言

Hausdorff算子在调和分析中有着悠久的历史,从最初的级数求和逐渐延伸到Hausdorff 算子求和,并且它在复分析及偏微分方程等分支中有着广泛的应用.通常,一维Hausdorff算子定义为

(1)

一维Hausdorff 算子已经得到较深入的研究[1-2].它在Rn中有很自然的2种推广,分别为:

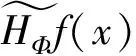
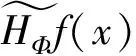
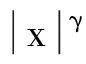
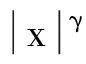
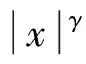
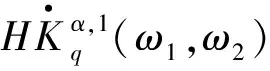
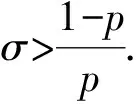
本文将采用记号AB表示存在不依赖主要变量的常数C,使得A≤CB.采用记号A≃B表示存在不依赖主要变量的常数c和C,使得cA≤B≤CA.特别指出,常数c,C在文中不同的位置,可能取值不同.

1 主要定义

首先,本节介绍一些相关空间的基本定义.

记Bk={x∈Rn:|x|≤2k},Δk=BkBk-1,k∈Z且χk=χΔk为集合Δk的特征函数.

其中,

(2)

当p=∞或q=∞时取通常的极限情形.

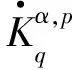
(3)

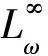
2 主要引理

接下来给出需要用到的相关引理.

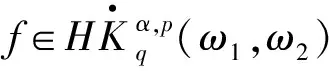
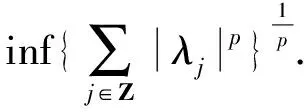
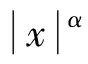
引理3[17]令ω∈Ap,1≤p<∞,则对任意的可测子集E⊂B,有

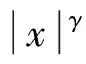
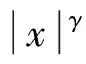
引理4证毕.

3 定理1的证明

由式(2)及Minkowski不等式得

(4)

(5)

综合式(4)、式(5)、引理4及|y|≃2j得

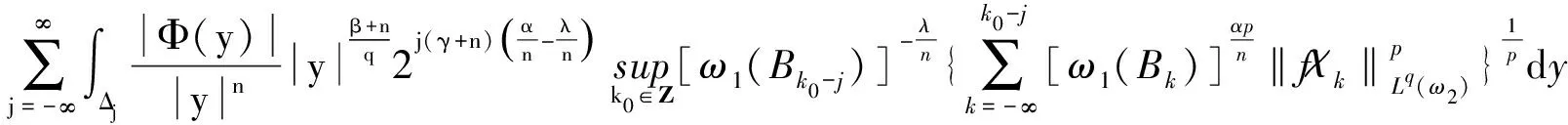
定理1证毕.

4 定理2的证明

首先估计‖(HΦf)χk‖Lq(ω2).由式(3),通过极坐标分解和变量替换得

其中,r-1Δk表示集合{x:rx∈Δk}.利用Hölder不等式和极坐标分解得

(6)

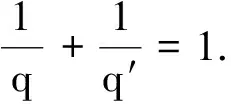
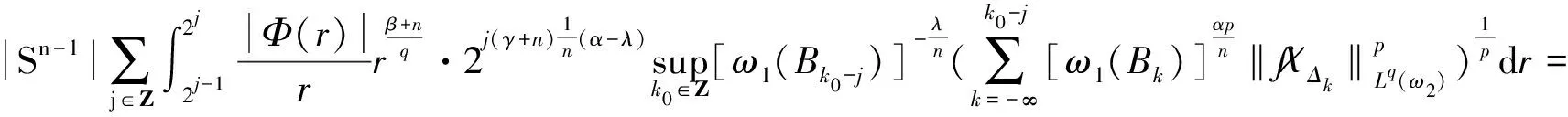
定理 2 证毕.

5 定理3的证明

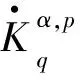
其中

supp(bk,j)⊂B(0,tρ)⊂B(0,2jρ).

以下估计bk,j的尺寸条件.利用Minkowski不等式得

由变量替换得

因此,由极坐标变换、Hölder不等式及ak的尺寸条件(即定义4中的2))得

(7)

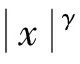
(8)

结合式(7)与式(8)得

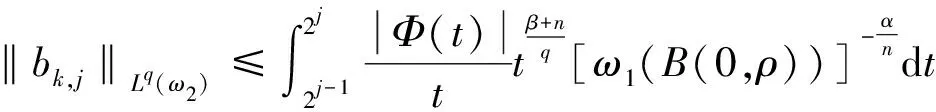
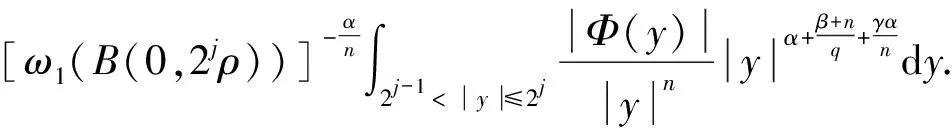
于是,记

bk,j(x)=ck,jAk,j(x).

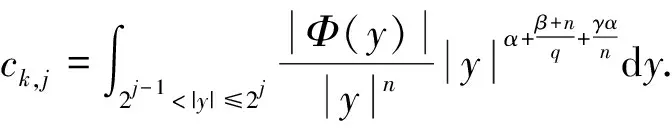
‖Ak,j‖Lq(ω2)

易见,Ak,j(x)的支集为

supp(Ak,j)=supp(bk,j)⊂B(0,2jρ).

利用极坐标分解、富比尼定理、变量替换及ak的消失性(即定义 4中的3))得

情形2当p=1时,有

综上即得定理3结果.定理 3 证毕.

参考文献：

[2]Liflyand E,Miyachi A.Boundedness of the Hausdorff operators inHp(0

[3]Chen Jiecheng,Fan Dashan,Li Jun.Hausdorff operators on function spaces[J].Chinese Annals of Mathematics Series B,2012,33(4):537-556.

[4]Hussain A,Gao A.Multidimensional Hausdorff operators and commutators on Herz-type spaces[J].J Inequal Appl,2013,2013(1):1-12.

[5]Komori Y,Shirai S.Weighted Morrey spaces and a singular integral operator[J].Math Nachr,2009,282(2):219-231.

[6]Lerner A K,Liflyand E.Multidimensional Hausdorff operators on the real Hardy spaces[J].J Aust Math Soc,2007,83(1):79-86.

[7]Andersen K F.Boundedness of Hausdorff operators onLp(Rn),H1(Rn) andBMO(Rn)[J].Acta Sci Math,2003,69(2):409-418.

[8]Gao G,Jia H.Boundedness of commutators of high-dimensional Hausdorff operators[J].Journal of Function Spaces and Applications,2012,2012(3):1-12.

[9]匡继昌.加权Morrey-Herz空间上的广义Hausdorff算子[J].数学学报:中文版,2012,55(5):895-902.

[10]高贵连,樊云.多线性Hausdorff算子的Sharp估计[J].数学学报:中文版,2015,58(1):153-160.

[11]陶双平,任转喜.n维Hausdorff交换子的加权估计[J].数学学报:中文版,2014,57(2):351-364.

[12]Ruan Jianmiao,Fan Dashan.Hausdorff operators on the weighted Herz-type Hardy spaces[J].Math Inequal Appl,2016,19(2):565-587.

[13]邹仕超,朱相荣.Hausdorff算子在加权Herz型Hardy空间上的有界性[J].浙江师范大学学报:自然科学版,2017,40(1):24-30.

[14]Lu Shanzhen,Yang Dachun.The weighted Herz-type Hardy space and its applications[J].Sci China Ser A,1995,38(6):662-673.

[15]Lu Shanzhen,Yang Dachun.The decomposition of weighted Herz spaces onRnand its applications[J].Sci China Ser A,1995,38(2):147-158.

[16]Grafakos L.Modern Fourier Analysis[M].3rd.New York:Springer,2014.

[17]Stein E M,Weiss G.Introduction to Fourier analysis on Euclidean spaces[M].Princeton:Princeton University Press,1971.