列控运营风险可预测度的计算方法研究
郭荣昌,赵小娟,范多旺
(兰州交通大学 自动化与电气工程学院,1.博士研究生,
根据铁路中长期发展规划,“十三五”期间全国新建铁路将不低于2.3万km,总投资不低于2.8万亿元,到2025年全国高铁将建成“八纵八横”网络[1]。随着我国高铁的快速发展,高铁运营安全问题显得尤为重要,列控系统作为铁路系统中安全相关系统,在保证列车安全运行方面发挥着关键作用,列控运营的风险管控已成为当前高铁发展的重大研究课题之一。
目前风险评价中使用较为广泛的是美国军用标准MIL-STD-882B《系统安全大纲要求》中推荐的风险矩阵评价方法,该方法将系统风险评价等同于对风险发生的可能性(或频率)和后果的严重度进行评价,并定性地将风险的可能性、严重度和风险评价结果分为若干等级,并对各级做相应的参考性描述[2]。列控相关国际标准EN 50126中也采用此风险矩阵方法[3],如表1所示。
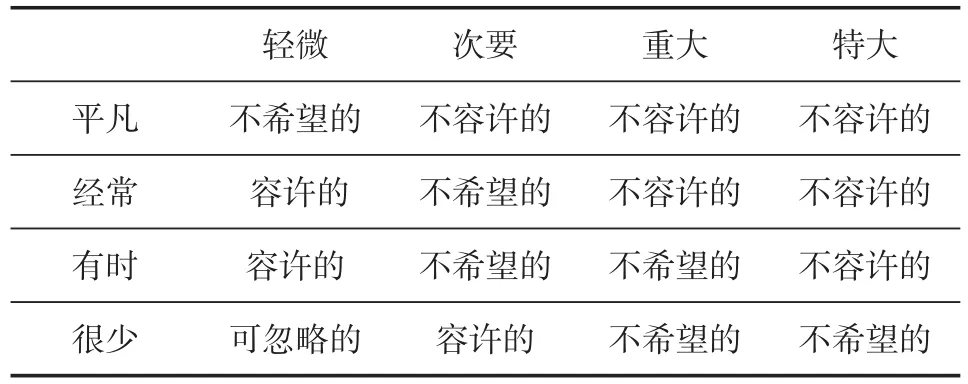
表1 风险矩阵
风险矩阵使用方便,简单易懂。但是就风险的本质属性来讲,风险具有不确定性、可控性、可变性和危害性四个属性,二维风险矩阵方法只能评价风险的不确定性和危害性,而没有考虑可控性和可变性。鉴于此不足,国内外风险评估研究领域的学者在二维风险矩阵的基础上提出了一些适用于特定行业和特定领域的三维风险评价模型。文献[2]中提出了一种考虑危险控制水平的三维风险评价模型;文献[4]中提出了一种适用于航空领域的考虑风险反映时间的三维风险矩阵;文献[5]中提出了一种适用于煤矿重大危险源风险分析的考虑风险因素重要度的三维风险矩阵;文献[6]中提出了一种适用于矿山采空区的考虑风险重要度的三维风险矩阵;文献[7]提出了一种考虑消费者脆弱性的消费品生命周期安全评价的三维风险矩阵模型。
笔者对列控运营风险可预测度计算方法的主要研究如下所述。
1 可预测度的三维风险矩阵模型
1.1 风险可预测度的定义 即人员在特定时间内采取措施预测化解风险的能力。风险可预测度从主客观两方面因素体现其对风险的影响,主观因素包括人对风险的反应能力和处理水平等,客观因素包括对风险的处理时间等。将风险定义为风险严重度、可预测度和发生可能性的函数,如式(1)所示:

式1中H表示风险评价结果,r表示风险严重度,c表示风险可预测度,p表示风险发生可能性。
风险的可预测度与人的受教育水平、风险的控制措施、人员安全素质、专业水平、经验、行动能力等因素有关。笔者按照人员对风险处理的期望结果,将风险预测度分为4个等级,如表2所示。

表2 风险可预测度
2 风险可预测度计算
2.1 计算方法 本文采用G1法和模糊数评价矩阵来计算风险的可预测度,基于G1法和模糊数评价矩阵的风险可预测度评价框图如图1所示。
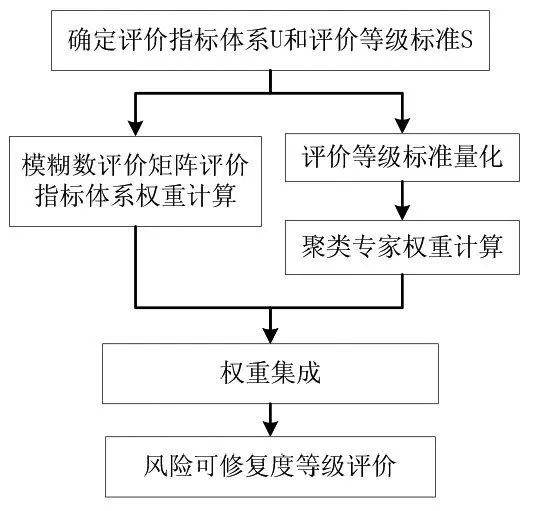
图1 风险可预测度评价框图
2.2 指标体系及标准的确定 即确定可预测度评价指标体系U和评价等级标准S。影响列控系统风险可预测度的因素很多,比如人员素质、天气情况、反应时间等等,总体可将这些因素归纳为人的因素、其他因素两个方面。建立列控系统风险可预测度评价指标体系U,如图2所示,U={U1,U2...,Un},n为影响因素个数。

图2 风险可预测度评价指标体系
依据表2中给出的可预测度等级,建立风险可预测度评价等级标准S={S1,S2,S3,S4}={完全可预测修复,基本可预测修复,基本不可预测修复,完全不可预测修复}。依据本课题研究成果,将专家评语中的可预测度等级置于连续的语言标尺上,采用百分制打分,建立风险可预测度评价等级标准S1,S2,S3,S4如表3所示。专家评估矩阵记为A。
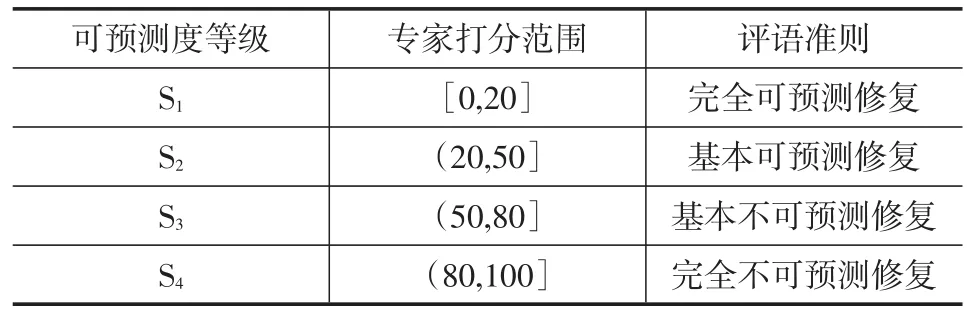
表3 评判标度定义
2.3 权重计算方法 考虑到专家的经验、专业等的不同,在专家权重上不能简单的采用同等权重,本节采用G1法来计算专家权重,具体的计算过程这里不再叙述。G1法计算过程参见文献[8,9]。
考虑到评价指标各因素对风险可预测度的影响程度不同,为突出可靠因子的重要性,降低不可靠因子对评价结果的影响,合理的计算评价指标体系权重,本文采用基于模糊数评价矩阵的评价指标体系权重算法。该算法能够很好的解决传统评价方法的不足,结果比较客观。该算法具体步骤如下:
1)模糊数评价矩阵运算规则
设模糊判断矩阵P=(P͂ij)m×n,其中P͂ij=(P͂aij,P͂bij,P͂cij)为 三 角 模 糊 数 ,并 且 0<Paij≤Pbij≤Pcij≤1,∀i,jϵI,若矩阵P͂满足:
①Paii=0.5,Pbii=0.5,Pcii=0.5,∀i;
②Paij+Pcij=1,Pbij+Pbji=1,Pcij+Pcji=1,i≠ j,∀i,j
则称P͂为三角模糊数互补判断矩阵。其中P͂ij表示因素ui相对于ui的重要程度。
2)评价指标体系权重计算
(1)由上述可知已建立评价指标体系U={U1,U2...Un},等级标准 S={S1,S2,S3,S4},专家集 X={X1,X2…Xk}和专家权重W={w1,w2…wk}。
(2)加权集成各专家的评判结果
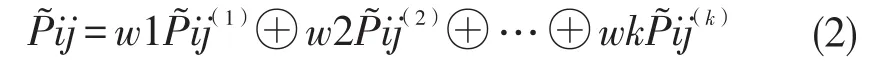
式2中,Wi为加权系数,且
(3)计算关于风险因素ui的模糊综合评价值v͂i
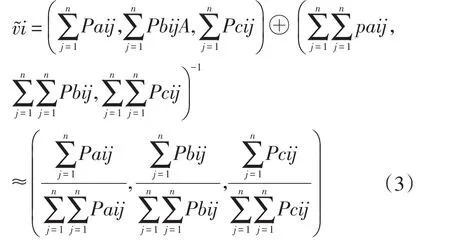
(4)计算模糊综合评价值的期望值
的左期望值为:ER=(Pai+Pbi)∕2;右期望值为ER=(Pbi+Pci)∕2,则͂的期望值为:
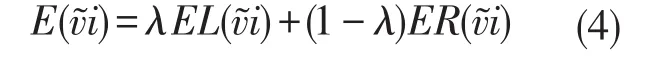
式4中,λ为乐观-悲观系数,0≤λ≤1,取决于专家的风险态度。当λ>0.5时,说明专家是悲观的;当λ=0.5时,说明专家表示中性的;当λ<0.5时,说明专家是乐观的[10,11]。这里取λ=0.5,则期望值计算式为

期望值越大说明其对应的模糊评价之越大。
(5)计算排序权重

权重排序,Qi越大,相应的指标越重要,Q为指标权重向量
2.4 结果集成 采用综合评判法对专家评价矩阵A、专家权重W和风险因素权重Q,最终得到风险可预测度评价结果B。
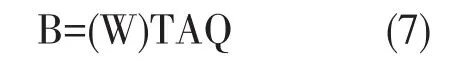
3 实例
以动车发车时由双黄码掉无码为例,运用本文提出的算法进行风险可预测度评估,验证其正确性和有效性。
3.1 确定评价指标体系U和评价等级标准S 依据风险因素完整性原则,建立评价指标体系U={险情识别时间,人员处理能力,风险所需修复时间,现有风险修复处理能力,电磁环境故意破坏等人为因素,雨雪雷电等自然环境情况,风险可控时间}。建立评价等级标准S={完全可预测修复,基本可预测修复,基本不可预测修复,完全不可预测修复}。
3.2 专家评估 邀请10位专家结合现场情况、设备状态、人员情况等资料对双黄码掉无码故障进行风险可预测度评估。采用G1法对专家权重进行计算,得到专家权重W=[0.1118 0.1118 0.1118 0.1016 0.1016 0.1016 0.1016 0.0924 0.0924 0.0924]T。同时,专家给出评价矩阵A。

3.3 评价指标体系权重计算
1)维护人员因素权重计算
所有专家对维护人员因素进行打分,加权集成各专家的评判结果,得到维护人员因素模糊判断矩阵

由式3得出风险因素ui的模糊综合评价值

根据式5取λ=0.5得出期望值为:
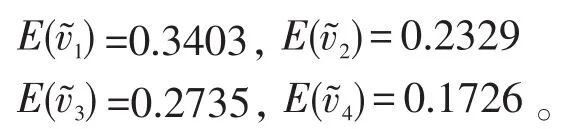
根据式6计算出指标权重排序向量:2)其他因素权重计算
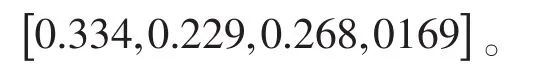
加权集成各专家的评判结果,得到其他因素模糊判断矩阵

由式3得出风险因素ui的模糊综合评价值为:͂=(0.2245,0.2778,0.3415)

根据式5取λ=0.5得出期望值为:
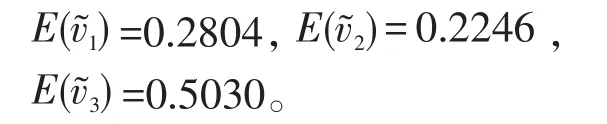
根据式6计算出指标权重排序向量:
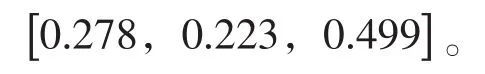
3)权重集成
对维护人员因素权重和其他因素权重进行加权集结,得到模糊判断矩阵

由式3得出风险因素ui的模糊综合评价值为:≈(0.619,0.675,0.7368),

根据式5取λ=0.5得出͂期望值为:E(͂)=0.6765,E(v͂2)=0.3260。
根据式6计算出指标权重排序向量:

将上述各因素权重进行集结得到风险因素权重矩阵:

3.4 结果集成 依据式7,有:

依据本文提出的可预测度计算方法进行双黄码掉无码故障的风险可预测度等级评估,得到的评估结果为12.37,对应本文建立的可预测度等级表,可以得到评价结果为完全可预测修复的。也就是说风险是可以完全消除的。这与实际相符,同时也说明本文可预测度计算方法的有效性和可用性。
4 结束语
本文在研究列控运营风险评估理论和技术的基础上,从风险本质属性模糊性和随机性的角度出发,建立了列控运营风险评价的三维矩阵模型;将G1法和模糊数理论引入到可预测度的计算之中,客观科学的评估了列控运营风险的可预测度等级,实例证明了本文方法的可用性和有效性。本文为现场列控运营的风险评估提供了更加科学的方法,具有一定的应用价值。
[1]中华人民共和国铁道部.中长期铁路网规划[Z].2008.
[2]吴穹,张春艳.三维危险评价方法的探讨[J].沈阳航空工业学院学报,1994,26(02):47-51.
[3] European Committee for Electrotechnical Standardization.EN50126 Railway applications- The specification and demonstration of Reliability,Availability,Maintainability and Safety[RAMS][S].Brussels:European Committee for Electrotechnical Standardization,2003.
[4] 赵廷弟,戎梅,焦健.三维安全风险评价模型的初探[C].大型飞机关键技术高层论坛暨中国航空学会2007年学术年会论文集.深圳:中国航空学会,2007,591-596.
[5]罗慈友,蒲源源,刘广建.基于三角模糊数的煤矿重大风险源分析[J].中国矿业,2014,12(08):83-87.
[6]马海军,黄德镛.采空区三维风险评价模型研究[J].沈阳航空工业学院学报,1994,415(01):139-141,146.
[7]胡晓运,林璐瑶,汤万金,李仲学,赵怡晴,李翠平.消费品生命周期隐患识别与风险评价的三维矩阵方法[J].系统工程理论与实践,2014,34(05):1213-1218.
[8] Lu Jing,Wang Yao.A Safety Assessment of China's Crude Oil Import Based on G1 Method[J].Procedia-Social and Behavioral Sciences,2013,96:1738-1744.
[9] 郭亚军.综合评价理论与方法[M].北京:科学出版社,2002
[10]曽祥纪,蒋惠国.基于三角模糊数的综合评价法在互通立交方案选取中的应用[J].武汉理工大学学报,2008,32(02):543-546.
[11]司书宾,孙树栋,韩光臣,王军强.基于三角模糊数的综合保障评价指标权重分析[J].西北工业大学学报,2004,22(06):689-694.

