高速凸轮变系数多项式凸轮曲线的研究

赵漫漫ZHAO Man-man 吴 佳 何雪明 - 钱志芳 -

(1. 无锡机电高等职业技术学校，江苏 无锡 214122；2. 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122)

凸轮机构几乎能够完成各种变速运动，可按需调节速度，精度高、成本低，在现代包装机械中仍应用颇多，尤其在一些食品包装机械中，如饮料灌装机、旋盖机等。为了使这些机械运作的振动和噪声更小，凸轮机构的运行精度必须得到保证，而对凸轮曲线设计进行优化是提高其运行精度最有效、最关键的方法。牧野洋[1]较早提出了一组简谐梯形组合凸轮曲线，由于该曲线较以往曲线通用性较好，使得简谐梯形组合凸轮曲线在凸轮机构的设计中得到了极大的应用。肖正扬等[2-3]研究了凸轮曲线各个特性参数值对凸轮机构的影响以及各参数之间的影响关系，并进行了动力学响应分析。而现阶段高速凸轮机构的设计大多采用多项式凸轮曲线，相较于简谐梯形组合凸轮曲线，多项式曲线只要取足够高的幂次数，它的高阶导数便总是连续的，因此更适用于高速凸轮机构[4]。刘昌祺等[5]总结了数种多项式凸轮曲线的表达式。葛正浩等[6]给出了多项式凸轮曲线的通用表达式以及各种边界条件对应的解决方法。巨刚等[7]得出七次以上的运动规律曲线在加速度这个范畴内具有永远的连续性、无冲击现象的结论，并且证实了高次多项式凸轮的受力或功率波动程度即高次多项式运动规律凸轮在运转过程中的平稳程度与次数有关。

由于多项式曲线良好的高阶导数连续性，因此设计时只要增加相应的次数，便可实现无限高次导数连续。但理论上可以实现的高阶多项式凸轮曲线在工程中却未必实用，当多项式次数升高后会增大加工难度，同时降低加工精度，从而无法实现相应的运动规律。由于现有的标准多项式凸轮曲线设计方法无法兼顾以上几点，因此本研究着重研究低阶多项式(阶次十一以下)凸轮曲线，在此基础上寻找尽量同时满足运动学和动力学的多项式凸轮曲线。

1 标准多项式凸轮曲线

标准多项式凸轮曲线的设计方法是通过两端的约束条件，求解出多项式方程未知数，从而得到标准多项式凸轮曲线。标准4-5-6-7多项式凸轮曲线设计方法：在升程起始位置位移零阶导数S0、一阶导数S0(1)(速度V)、二阶导数S0(2)(加速度A)、三阶导数S0(3)(跃度J)均为0，升程终止位置位移零阶导数S1=1，一阶导数S1(1)、二阶导数S1(2)、三阶导数S1(3)均为0，则标准4-5-6-7多项式凸轮曲线约束条件可写为：

(1)

标准4-5-6-7多项式凸轮曲线方程见式(2)。

(2)

与其它凸轮曲线相比，标准的多项式凸轮曲线设计方法较为简单，且动力学响应性能较好，故在高速凸轮设计中得到了一定的应用。但该凸轮曲线的各特性参数已为定值，即运动学特性和动力学特性固定不变。在高速凸轮工程设计中，往往需要兼顾二者，或者在满足动力学性能情况下对系统的最大加速度Amax或者最大速度Vmax进行控制。要实现以上控制条件，必须要求多项式曲线具有可变性。

2 变系数多项式凸轮曲线

2.1 七次变系数多项式凸轮曲线

为了实现多项式曲线可变，将标准七次多项式曲线的两端约束条件由三阶导数连续降低为二阶导数连续，并加入最大加速度Amax可变的约束条件，求解多项式函数，通过“牺牲”两端导数连续性来实现多项式曲线的变化。

本研究的凸轮曲线为对称双停留曲线，可得该凸轮曲线在T=0.5处取得最大速度V0.5=Vmax，此时A0.5=0，再根据凸轮曲线两端的约束条件，可得变系数七次多项式凸轮曲线约束条件为：

(3)

因为七次多项式凸轮曲线为二阶导数连续，故其曲线方程见式(4)。

(4)

联立约束条件，可解得3-4-5-6-7多项式凸轮曲线位移方程为：

S=(-32Vmax+70)t3+(160Vmax-315)t4+(-288Vmax+546)t5+(224Vmax-420)t6+(-64Vmax+120)t7。

(5)

通过给出不同的最大加速度值Vmax，可以得到相对应的两端二阶导数连续3-4-5-6-7多项式凸轮曲线，凸轮曲线的运动学和动力学性能也发生相应的变化，设计人员可以根据实际的设计要求选择最大速度Vmax。

为了研究最大速度Vmax可行域，依次取Vmax=1.3，1.5，1.7，经计算可以得出相应的速度图谱见图1。研究发现随着输入的最大速度减小，速度波峰逐渐减小，当Vmax=1.3时，速度曲线由原来的单峰变为双峰，即无法取得设计规定的最大加速度，说明七次变系数多项式最大速度Vmax存在下限值。通过计算分析，发现Vmax下限值为1.458～1.459，为了方便研究，取Vmax下限值为1.46，即该多项式凸轮曲线的最大速度值Vmax取值范围为1.46～。

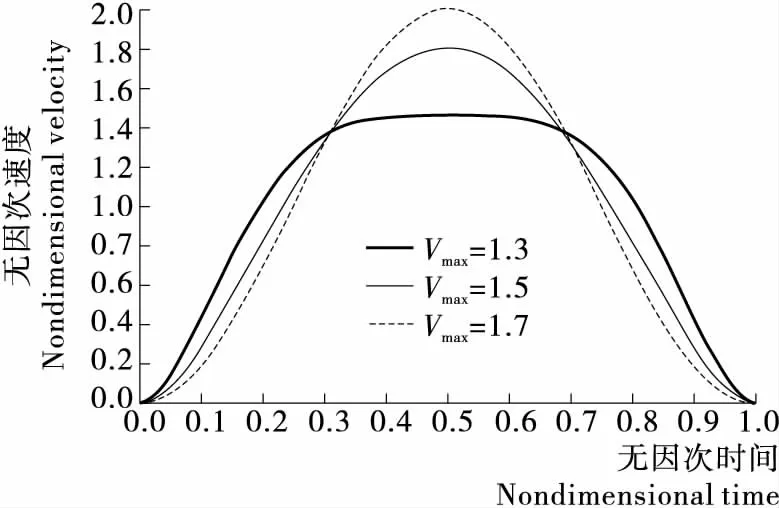
图1 七次变系数多项式凸轮曲线速度图谱Figure 1 Speed map of 7 power coefficient polynomial cam curve

考虑到曲率半径以及惯性力的大小，设计中追求较小的最大速度Vmax，过大的最大速度Vmax并没有意义，因此取Vmax研究区间为1.46～2.00，在此区间内初步研究凸轮曲线各特性参数的变化，为该曲线下一步的研究提供指导，在研究区间内取值Vmax=1.46，1.80，2.00，并绘制相应的凸轮曲线图谱，见图2。

为了更好地考查各特性参数的变化趋势，计算出不同最大速度对应的各特性参数最大值(见表1)。

表1七次变系数多项式凸轮曲线特性参数

Table 1 Characteristic parameters of 7 power variable coefficient polynomial cam curve

VmaxAmaxJmaxQmaxAVmax 1.4606.499 2139.681 953.600 09.488 8 1.8005.623 874.40648.000 010.122 9 2.0006.328 739.00256.570 812.657 5

通过对凸轮曲线图谱2以及表1的分析可以看出，随着最大速度Vmax的变化，凸轮曲线各个特性参数都发生了较大的变化，且变化规律各不相同，从而呈现出不同的运动学和动力学特性，因此对于Vmax的选择，必须做深入研究。

2.2 九次变系数多项式凸轮

七次变系数多项式凸轮曲线可以实现端点二阶导数连续，无法满足高速凸轮设计，为了增加端点处导数的连续性，同时考虑加工的精度、成本，研究九次变系数多项式凸轮曲线。仿照七次变系数多项式凸轮曲线设计方法，九次变系数多项式两端要实现三阶导数连续，故其位移方程最低次项应为4次，参照七次变系数多项式条件分别设置目标函数、约束条件可求得九次变系数多项式曲线位移方程通式见式(6)。

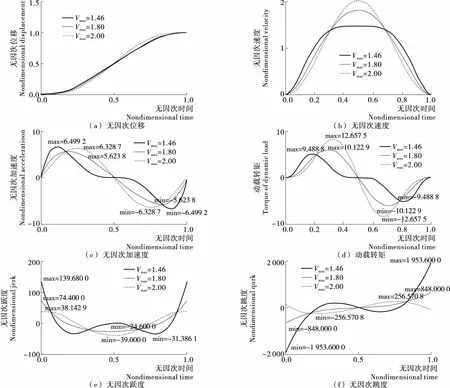
图2 七次变系数多项式凸轮曲线各特性参数变化图谱Figure 2 Variation of each characteristic parameter of 7 power coefficient polynomial cam curve

S=(-128Vmax+315)t4+(768Vmax-1 764)t5+(-1 792Vmax+3 990)t6+(2 048Vmax-4 500)t7+(-1 152Vmax+2 520)t8+(256Vmax-560)t9。

(6)

研究发现，类似七次变系数多项式凸轮曲线的特性，九次变系数多项式凸轮曲线同样存在Vmax下限值，经计算得九次变系数多项式曲线的变化范围Vmax下限值在1.640 6与1.640 7之间，为了方便研究，取九次变系数多项式曲线Vmax下限值为1.641，在Vmax变化范围为1.641～2.200，对九次变系数凸轮曲线进行初步研究。

为了研究九次多项式曲线的变化趋势，分别绘制Vmax=1.641,2.000,2.500时九次多项式曲线各特性参数图谱，见图3。同时计算出各特性参数对应的最大值，见表2。

通过图3和表2可以看出，九次变系数多项式凸轮曲线实现了端点跃度J连续，各特性参数随最大速度的变化而变化，但变化趋势各不相同。

表2九次变系数多项式凸轮曲线特性参数

Table 2 Characteristic parameters of 9 power variable coefficient polynomial cam curve

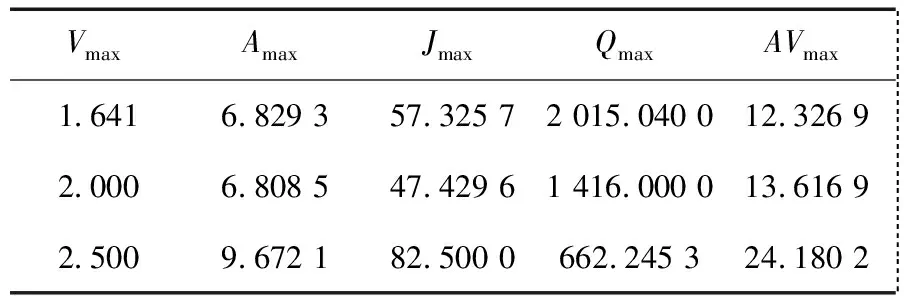
VmaxAmaxJmaxQmaxAVmax 1.6416.829 357.325 72 015.040 012.326 9 2.0006.808 547.429 61 416.000 013.616 9 2.5009.672 182.500 0662.245 324.180 2

2.3 十一次变系数多项式凸轮曲线

为了进一步提高凸轮曲线的动力学特性，在九次变系数幂函数凸轮曲线基础上，提出十一次变系数多项式凸轮曲线，位移方程最低阶次提高到五次，这样就可实现凸轮曲线方程两端四阶导数连续，参照七次变系数多项式设置约束条件可求得十一次变系数多项式曲线位移方程通式见式(7)。

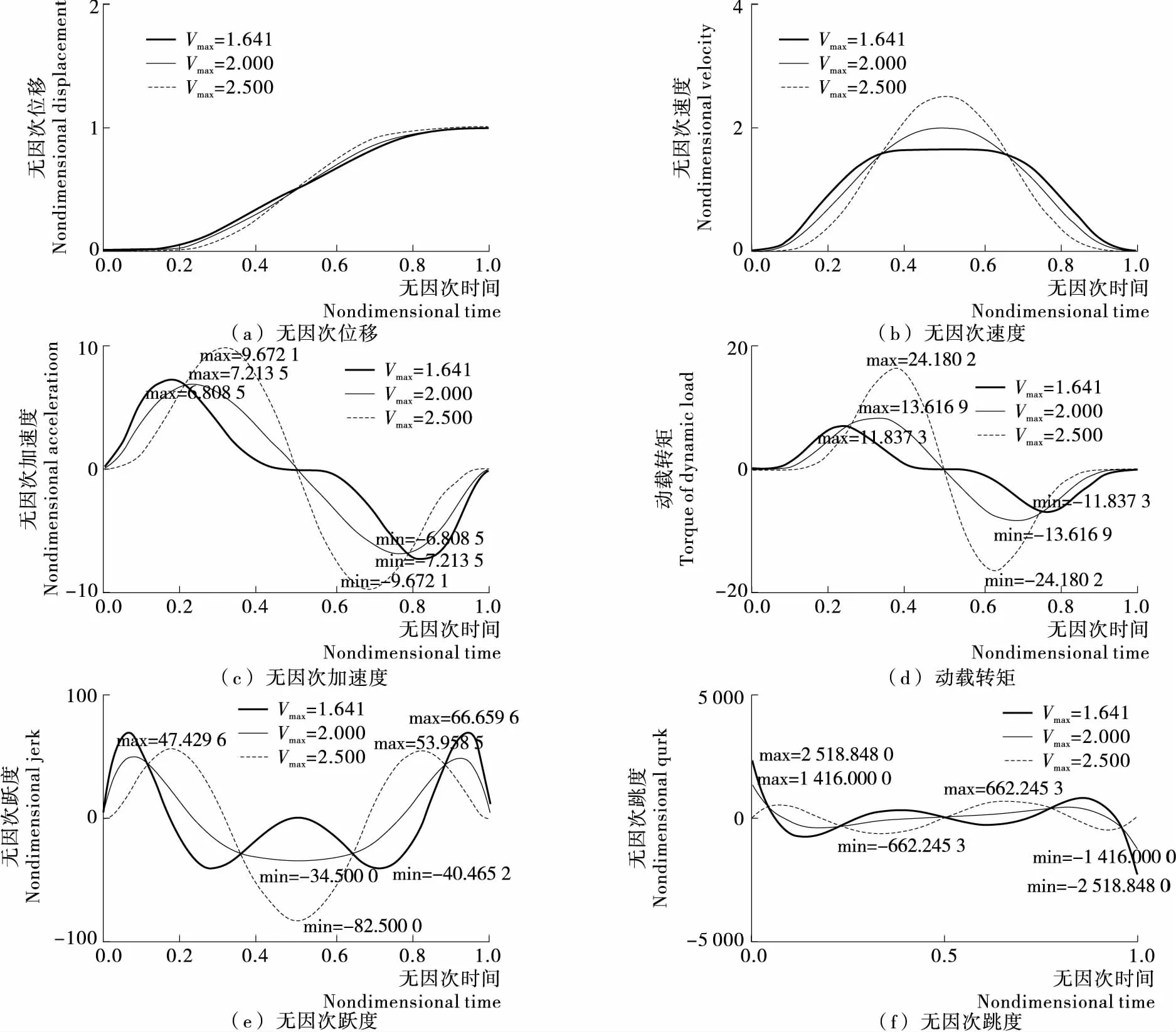
图3 九次变系数函数多项式凸轮曲线各特性参数变化图谱Figure 3 Variation of each characteristic parameter of 9 power coefficient polynomial cam curve

S=(-512Vmax+1 386)t5+(3 584Vmax-9240)t6+(-10 240Vmax+25 740)t7+(15 360Vmax-38 115)t8+(-12 800Vmax+31 570)t9+(5 632Vmax-13 860)t10+(-1 024Vmax+2 520)t11。

(7)

仿照七次变系数多项凸轮曲线，经过计算得出十一次变系数多项式曲线的变化范围下限值在1.804 6和1.804 7之间，为了便于研究，并与传统多项式曲线对比，取十一次变系数多项式曲线Vmax下限值为1.805，变化范围为1.805～2.707。为考察十一次变系数多项式曲线的变化趋势，在Vmax=1.805，2.000，2.707时，计算并绘制十一次变系数多项式曲线各特性参数图谱(见图4)，为方便对比，计算各特性参数的最大值(见表3)。

通过对表3分析可以看出，与七次和九次变系数多项曲线一样，十一次变系数多项凸轮曲线各特性参数并未随着最大速度的变大而变大，变化趋势各有不同，变化范围差距较大。

分析图4及表3可知，十一次变系数多项式实现了跳度Q的连续，且各特性参数在整个周期内变化平稳、无突变。

表3十一次变系数多项式凸轮曲线特性参数

Table 3 Characteristic parameters of 11 power variable coefficient polynomial cam curve

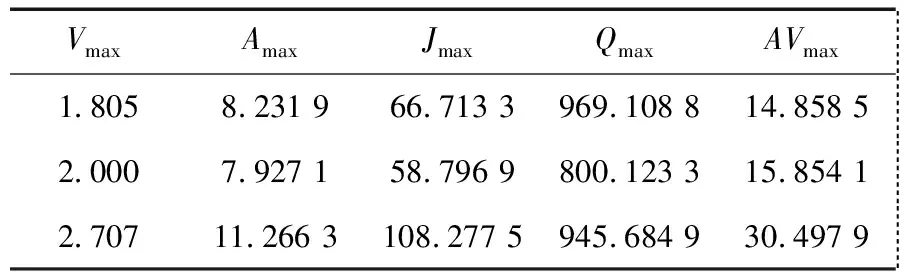
VmaxAmaxJmaxQmaxAVmax 1.8058.231 966.713 3969.108 814.858 5 2.0007.927 158.796 9800.123 315.854 1 2.70711.266 3108.277 5945.684 930.497 9

3 结论

通过对传统标准多项式凸轮曲线的研究，本研究提出了七、九、十一次变系数多项式曲线，并对凸轮曲线方程及特性参数进行计算，绘制了特性参数图谱，通过图谱分析可看出，该曲线各特性参数随着最大速度Vmax取值的变化而变化。综合3种变系数多项式最大速度Vmax下限值可以看出，为了提高动力学性能，增加多项式次数可提高凸轮曲线方程两端的可导性。但是最大速度Vmax下限值由七次变系数多项式的1.46提高到十一次变系数多项式的1.805时，虽然动力学性能提高，但运动学性能变差。可见在采用变系数多项式凸轮曲线时，对偏重于运动学特性的中低速凸轮机构，可以选取次数较低的凸轮曲线，对动力学性能要求较高的高速凸轮则可以选取次数较高的凸轮曲线。

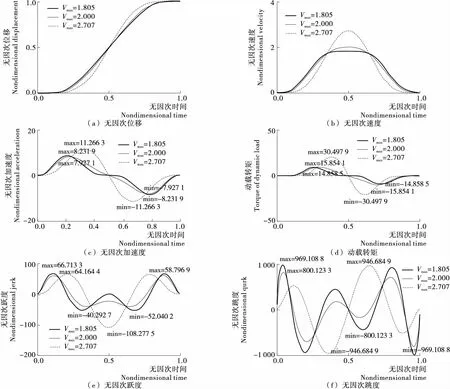
图4 十一次变系数函数多项式凸轮曲线各特性参数变化图谱Figure 4 Variation of each characteristic parameter of 11 power coefficient polynomial cam curve

[1] 牧野洋. 自动机械机构学[M]. 胡茂松, 译. 北京: 科学出版社, 1980: 30-33.

[2] 彭国勋, 肖正扬. 自动机械的凸轮机构设计[M]. 北京: 机械工业出版社, 1990: 55-65.

[3] 肖正扬, 杨洋, 刘晓云. 自动机械凸轮从动件简谐梯形通用运动曲线运动学优化[J]. 西北轻工学院学报, 1985(2): 22-32.

[4] 葛正浩, 肖敏, 屈毅, 等. 用于分度凸轮机构的谐波运动规律研究[J]. 机械设计, 2014, 31(7): 33-38.

[5] 刘昌祺, 牧野洋, 曹西京. 凸轮机构设计[M]. 北京: 机械工业出版社, 2005: 35-41.

[6] 葛正浩, 冯涛, 彭国勋. 可以任意增加局部控制条件的凸轮机构通用多项式运动规律[J]. 机械科学与技术, 1998, 17(6): 986-1 022.

[7] 巨刚, 袁亮, 刘小月. 凸轮机构高次多项式运动规律曲线研究及仿真分析[J]. 机械设计与制造, 2015(5): 107-109, 114.