秩和比法在真空湿热定型机性能评价中的应用

舒服华

（武汉理工大学职业技术学院，湖北武汉430070）

真空湿热定型机是生产高档运动鞋、皮鞋所必不可少的先进设备，是冷粘鞋成型新工艺的生产设备。它采用“真空熨烫，蒸汽雾化，活化干燥，强力鼓风”等技术对绷帮后的鞋子进行时效处理，以使结帮胶干燥固化，帮面饱满，清除绷帮过程中所产生的内应力，提高冷粘鞋的综合性能，使鞋不易变形。真空湿热定型机的性能和质量对制鞋生产效率和产品质量至关重要，科学评价其性能和质量对设备的设计、制造、选择、使用具有重要的现实意义。

秩和比法 (Rank Sum Ratio，RSR)是一个内涵极为丰富的统计分析方法，它融古典的参数统计与近代的非参数统计于一体，兼及描述性与推断性。针对性强，操作简便，使用效果明显[1-2]。本文利用秩和比法评价真空湿热定型机的综合性能，以利于提高评价的准确性和可靠性。

1 评价指标体系

XDXZ-6型真空湿热定型机主要由箱壳部分、传动部分、气动部分、真空部分、加湿、加热、置鞋箱、电器控制等主要部件组成。传动通过电磁制动、电机、减速机、链轮、链条带动六个内箱运转，内箱中装有托杆，可把鞋置于托杆上，气动部分通过气缸输入压缩空气带动箱盖开合。真空部分通过真空泵，真空管，电磁阀，滤清器，抽出内箱中气体，形成负压，加湿是利用压缩空气通过电磁阀吹入箱内形成雾。加热是在箱盖中装有加热棒，两盖合并后对鞋加热。根据XDXZ-6型真空湿热定型机的结构特点，其综合质量评价指标体系可分为以下8个部分。

1.1 箱壳部分

要求材料性能优良，尺寸符合要求，有足够的强度和刚度，成型工艺良好，联接牢固可靠，外表平整，无凸起、凹陷、毛刺等缺陷，涂装精细，颜色均匀、材料环保。

1.2 传递部分

要求传动部件运动灵活，无咔阻、磕碰、发热、冒烟等现象。传动效率高，传动比精确。齿轮、链、V带、轴承、联轴器等运动部件材质优良，加工精度高，润滑性能好，耐磨损、抗腐蚀，维护维修性好，使用寿命长。

1.3 气动部分

要求空压机与生产工艺匹配，供气量充足，产气效率高，能耗少，轻量化，防爆措施完善。电磁阀、调压阀、过滤器、油水分离器等气动元件性能优良，工作可靠，工位转换准确到位，气动管线能承压额定压力，安全系数高，密封性能好泄漏损失少，气动部分工作噪声小。

1.4 真空部分

要求真空泵性能优良，抽气能力强，抽气效率高，冷却循环系统运转正常，泵体工作时温升小，运动部件润滑优良，磨损小真空管材质量优良，耐高压，耐高温、耐腐蚀、耐磨损，真空仪表,真空阀门等控制元件工作可靠，真空度控制精确。真空部分密封性能好，噪音小。

1.5 置鞋箱

设计合理，有充足的承载能力，内部无塌陷、弯曲、扭曲变形，无剥落、斑秃、飞边等缺陷，箱门开关灵活，密封性好，单位容积鞋容量大，材料耐高温、耐高压、耐腐蚀、耐磨损。

1.6 加湿部分

加湿元件工作可靠，加湿迅速，湿度分布均匀，湿度控制精度高，节水，加湿动作精准，关停自如，管线密封性好，无渗漏开裂现象，材料耐腐蚀、防潮防锈。

1.7 加热部分

加热元件质量优良，升温迅速，温度分布均匀，热传播效率高，节能，温度控制精准，系统安全可靠，耐高温、无烫伤、火灾、触电等隐患。

1.8 电气控制系统

电机功率因素高，防潮防爆，接地保护和漏电保护好，电气控制箱稳固结实，操作方便，绝缘性能好，线路布置符合规范，导线容量足够，继电器、接触器，断路器等电气元件性能优良，工作可靠，安全系数高。

2 秩和比评价方法

2.1 基本原理

RSR法是一种有效的多指标评价方法。秩和比法的基本思想是在一个n行(n评价对象)m列(m个评价指标)矩阵中，通过秩转换，获得无量纲的统计量RSR，以RSR对评价对象的优劣进行排序或分档。评价对象的RSR越大，则越优。该评价方法计算简单，对数据信息要求低，抗干扰能力强，并可与其他许多数理统计方法互相沟通、移植和嫁接[3、4]。

2.2 评价步骤

2.2.1 数据规范化处理

对于传统的秩和比，不需要对数据进行规范化，不论何种量纲和数量级的数据，只需按数值的大小编秩即可，但对于加权秩和比，由于属性之间的量纲和数量级不同，对求权有一定的影响，因此需要对原始数据进行规范化处理。属性指标一般分为二类：效益型指标、成本指标。所谓“效益型指标”就是指标值越大越好；“成本型指标”则是指标值越小越好[5]。对于不同类型的指标，数据规范化方式不同。

当xij为效益型数据时，数据规范化方法为：

当xij为成本型数据时，数据规范化方法为：

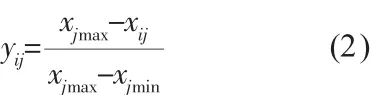
式中，xij为原始数据，yij为规范化数据；xjmin=min{xj1，xj2，…，xjn}；xjmax=max{xj1，xj2，…，xjn}。(j=1,2，…，m)。

2.2.2 确定指标的权重

评价对象综合性能为各评价指标性能的线性组合。由于各指标对其综合性能的重要程度不同，因此需要以权重的形式体现。文中以客观的熵值法确定权重。在信息论中，熵是对不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；反之，不确定性就越大，熵也就越大。这样可以通过计算熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响越大，所赋予的权重就越大。熵值法确定权重的具体步骤如下[6、7]：

(1)计算指标的比重

(2)计算指标的熵值

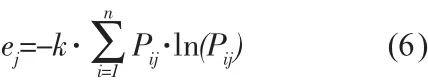
式中，k=1/lnn对于特殊情况当Pij=0时，取 lnPij=0。

(3)计算指标的差异系数

(4)计算指标的权重

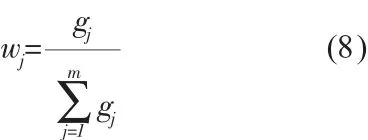
式中，Pij第 i评价单元第j指标的比重；ej第j个指标的熵值；gj第 j个指标的差异系数；wj第j个指标的权重(i=1，2，…，n；j=1，2，…，m)。

2.2.3 编秩[8]

编秩就是对每个评价对象的每个指标在同类中的优劣程度进行排序，即根据评价值对评价矩阵X=(xij)的每一列元素进行比较排出优劣次序。对于效益型指标从小到大编秩，成本型指标从大到小编秩，同一指标数据相同者编平均秩，秩越大表明属性值越优。对于数据已经规范化处理的评价矩阵Y=(yij)，直接按第一种情况编秩，由此将评价矩阵转化为秩矩阵，记为R=(rij)。

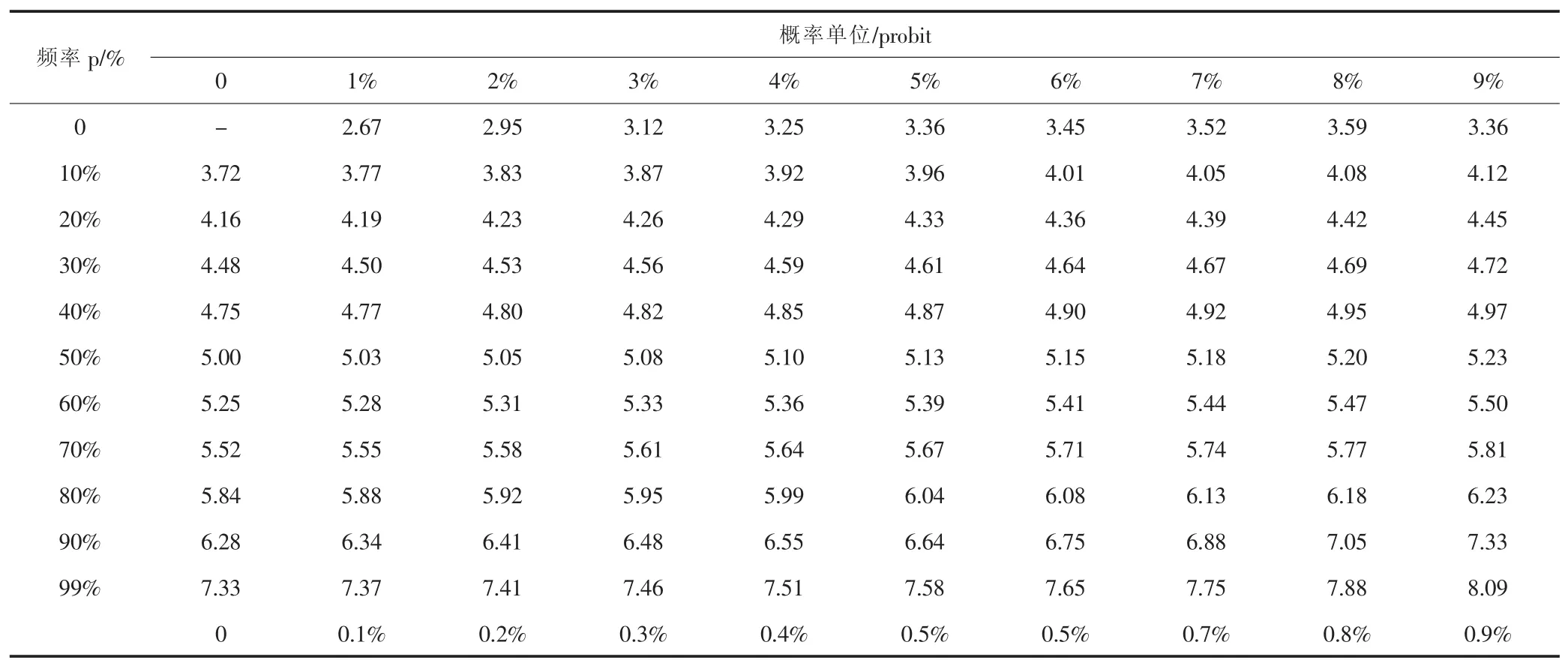
表1 p(百分率)与概率单位(probit)对照值

2.2.4 计算秩和比

秩和比指的是矩阵中行(或列)秩次的平均值，是一个非参数计量，具有0-1区间连续变量的特征。计算公式为

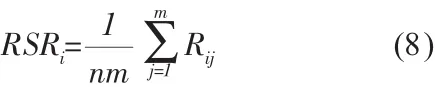
式中，RSRi为第i个评价对象的秩和比；Rij第i个评价对象的第j指标的秩，(i=1，2，…，n；j=1，2，…，m)。

当各评价指标的权重不同时，评价对象的秩和比为各指标秩的加权和。计算公式为：

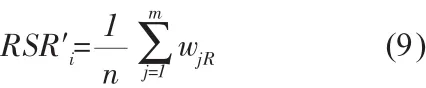
式中，RSR’i为第i个评价对象的加权秩和比；wj为第j个评价指标的权重，∑wj=1，(i=1，2，…，n；j=1，2，…，m)。

2.2.5 确定R SR的分布

虽然通过秩和比可以对评价对象进行排序，但这种排序是否有效或者可靠，是否有其他干扰因素影响了评价的结果，还需要进一步分析。分析的基本方法是进行统计回归。确定RSR的分布是重要的一步，其的任务是计算评价对象的概率单位值(probit)。首先编制RSR频率分布表；列出各组频数fi；计算各组累计频数∑fi；然后确定各组RSR的平均秩次R；最后计算向下累计频率pi(以百分率计)；最后一个累计频率按1-1/(4n)估计，将pi转化为评价对象的概率单位probit。计算公式为

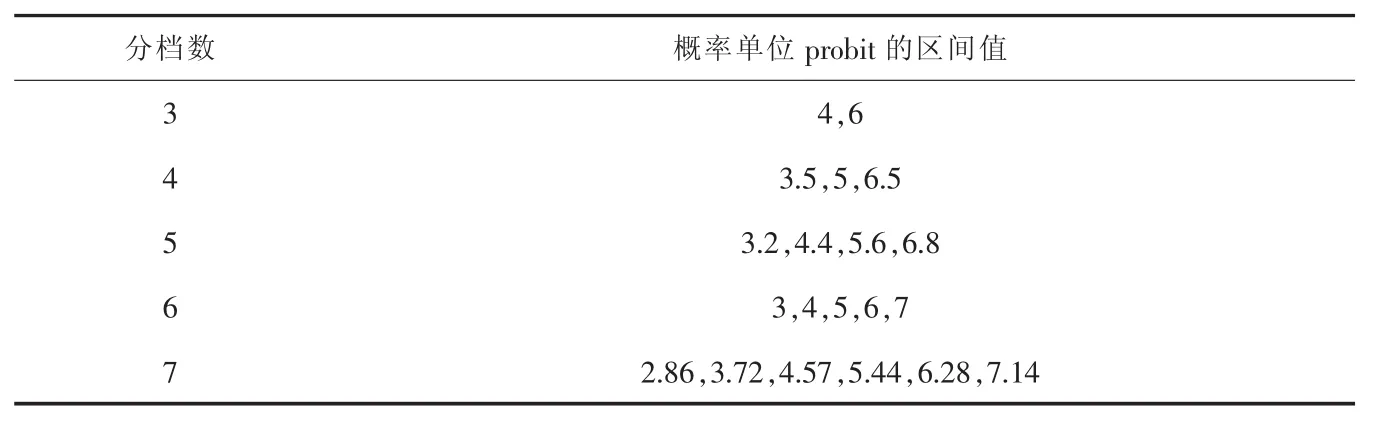
表2 常用的分档类型与概率单位值

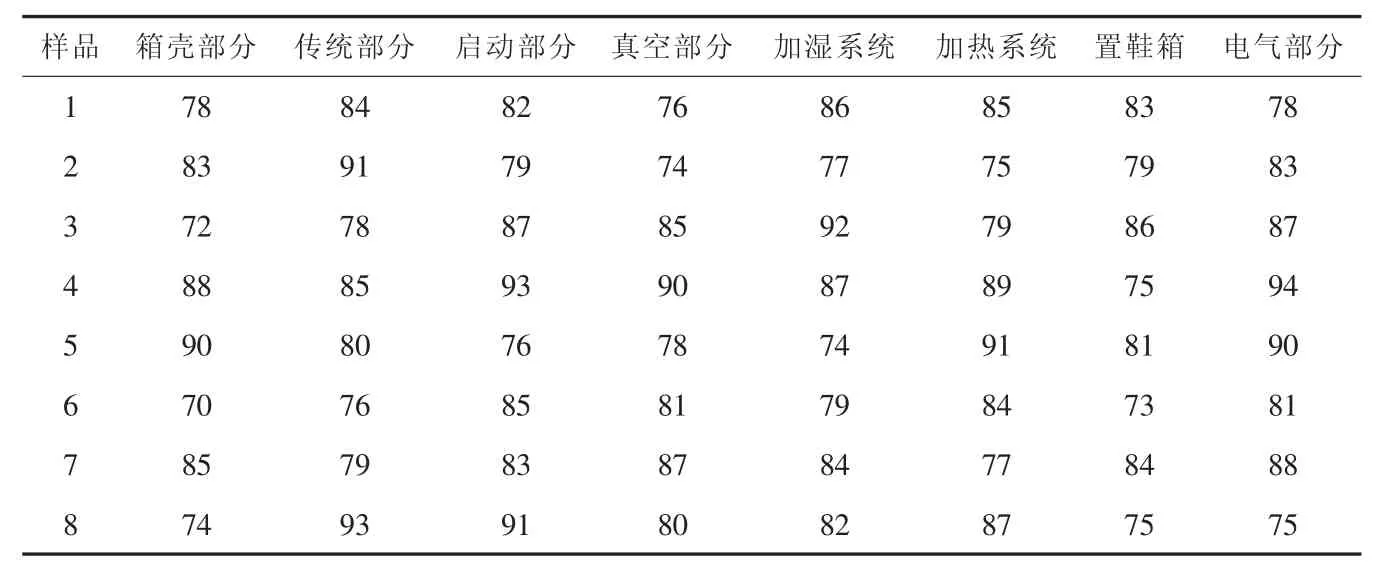
表3 待评价真空湿热定型机的性能指标值

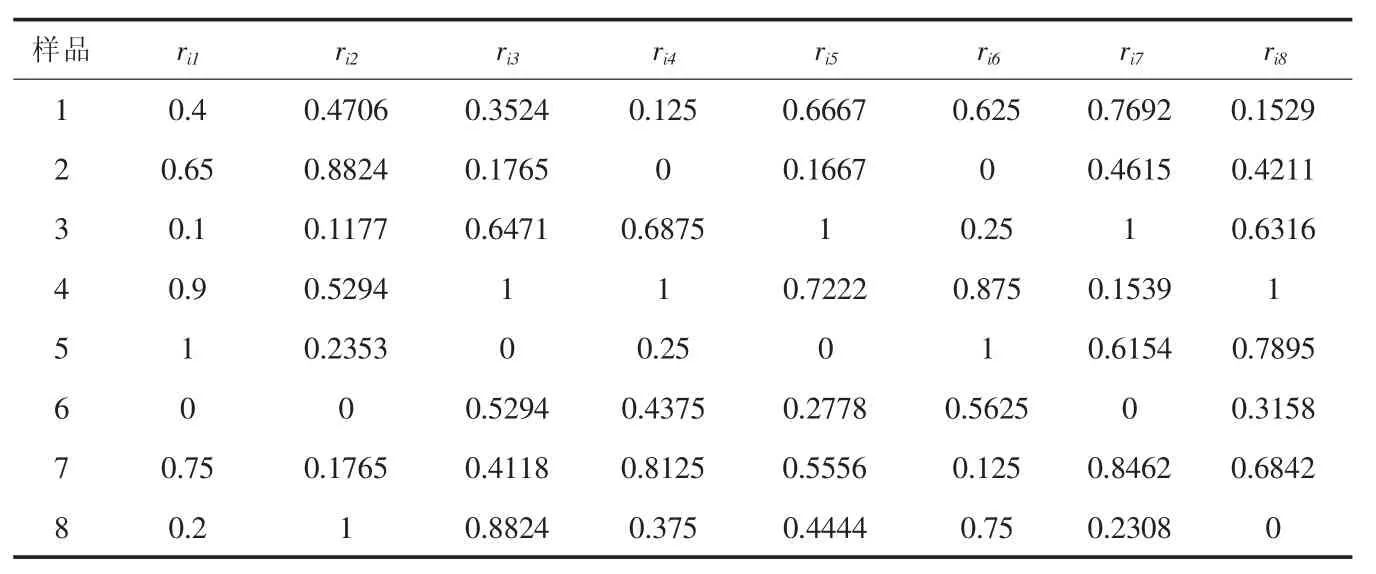
表4 数据规范化结果

式中，pi为第i评价对象向下累计频率；probiti为第i评价对象的概率单位值；u(·)表示pi的标准正态离差函数。

常用的p与probit值的对照表如表1所示，表中第1行和第1列对应值的和为百分率值pi，交叉处为相应的概率单位probit值，最后第1行和最后第1列对应值的和为99%以上百分率值pi，表中probit值以通过公式(11)的转化，可以直接通过pi查找对应的probit值。

2.2.6 计算回归方程

以累计频率pi对应的概率单位probiti值为自变量，秩和比RSRi为因变量，构造一元线性回归方程，目的是检验RSR法排序可信度，设一元直线方程为[8]

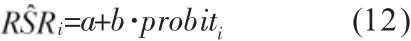
式中，a、b为回归方程的系数。

求出a、b和其他参数，据此对模型进行分析。

2.2.7 分档排序

根据回归方程计算得到的秩和比值，对评价对象进行分档排序。分档的依据是标准正态离均差u，常用的分档数为3～7档，其分别对应的概率单位probit值如表2。确定分档数量后，依据其对应的概率单位Probit临界值，根据评价对象的秩和比值进行分档。

2.2.8 模型的检验

(1)拟合优度检验(R2检验)

它是检验模型对样本观测值的拟合程度，指标为关联系数R2，R2越接近于1，说明实际值与预测值越接近，拟合优度越高，一般 R2＞0.7。

(2)显著性检验

它是检验自变量是否对因变量有显著线性影响。分为F检验、t检验、P检验，当要求 F＞F0.025(1，n-2)；t＞t0.95(n-2)，P＜P(0.25)=0.05时显著线性姣好。模型的显著性越高，评价的可靠性越大，评价模型越有效。

3 应用实例

以8台XDXZ-6型真空湿热定型机为研究对象。分别记为 S1、S2、S3、S4、S5、S6、S7、S8，选取箱壳部分、传统部分、气动部分、真空部分、加湿系统、加热系统、置鞋箱、电气部分8项性能参数作为评价指标，分别记为 C1、C2、C3、C4、C5、C6、C7、C8。8 台真空湿热定型机的8项性能指标检查结果如表3所示。

对真空湿热定型机属性指标数据进行规范化处理，其中，真空湿热定型机技术性能的8个指标全部为效益型数据，按式(1)进行规范化处理，结果见表4。

计算每个属性指标的权重。首先按式(5)计算各个指标的比重，结果如表5所示，然后按式(5)～(6)计算每个指标属性的熵值、差异系数，最后按式(7)计算每个属性指标的权重，结果见表5。

真空湿热定型机8个性能指标的权重分别为:

wj=(0.12918，0.12987，0.12147，0.12 562，0.12191，0.12530，0.12439，0.12224)

根据表5中数据，对每台真空湿热定型每个性能指标进行编秩，8台真空湿热定型机8个属性的秩次如表6。然后按式(9)计算加权秩和比，结果如表6。

此时，可以按照秩和比对8台真空湿热定型机的综合质量进行排序(结果见表7中的第一列)，根据秩和比大小8台真空湿热定型机综合质量由优到差的次序为：S4、S7、S3、S5、S8、S1、S2、S6。S4综合质量最好，S6综合质量最差。秩和比评价结果见图1。

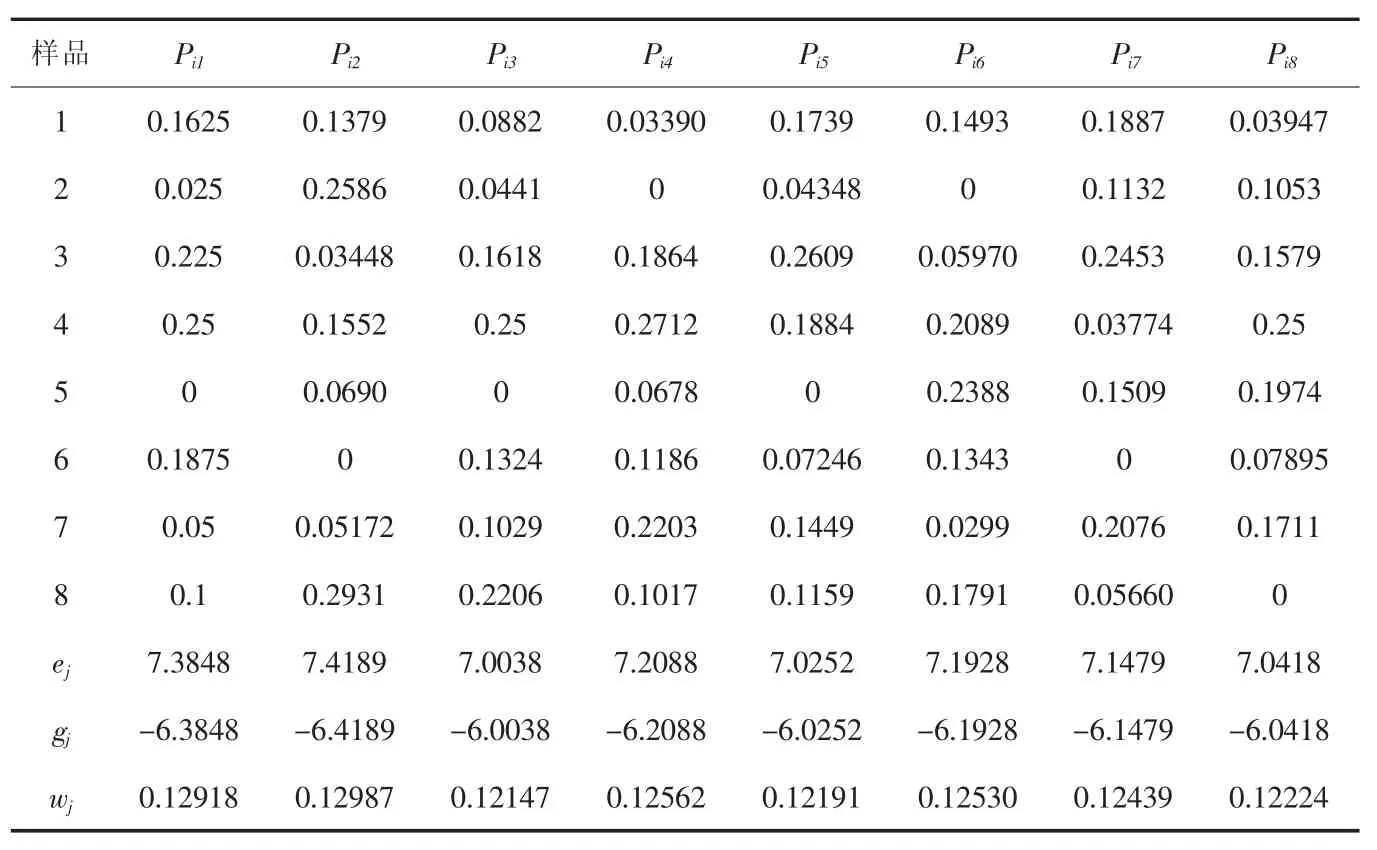
表5 评价真空湿热定型机性能指标的权重数据

虽然这8台真空湿热定型机的RSR值不同，但并不意味这些不同是有显著性的，或许因其他噪声因素的加入影响了RSR值，证明评价的真实性度也就不能令人信服，所以应该进行假设检验。此外，我们不仅希望要获得真空湿热定型机质量直观的印象，还希望知道它们更为详细的信息，因此对模型进行回归分析。首先按式(7)计算每个评价对象向下累计频率pi；然后按表1转化为概率单位，结果如表7。

以表7中的概率单位为自变量，秩和比为因变量，建立如式(12)的一元线性方程，求得系数如表8所示。即a=-0.18158，b=0.14224。

一元线性方程为：

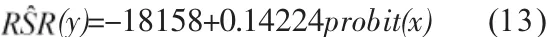
对回归方程进行检验，求出得R2、F、t、p及误差的方差σ，结果如表8。

从表8知，R2=0.93654，说明模型的相关 性 很 大 ，F=88.545＞F0.025(1，6)=8.81；t=9.409＞t0.95(6)=1.943、p=0.00008＜P(0.25)=0.05、σ=0.0015，很小，这些数据说明了模型具有极高的显著性，该秩和比模型对评价真空湿热定型机的性能有效，结果可靠。

一元线性回归模型的预测值如表7。一元线性回归方程见图2。

根据一元线回归方程计算得到的秩和比值，对评价8台真空湿热定型机进行分档。由于8台真空湿热定型机的最大小于 9，最小大于3，根据分档法则，分为3档比较合适，可将三个挡次的级别定义为“优秀”，合格”，“不合格”。分档结果为：S3、S7、S4属于“优秀”等级；S2、S1、S8、S5属于“合格”等级；S2属于“不合格”等级。根据不同档次概率单位probit值范围，按式(13)求出相应的RSR的范围结果见表9。

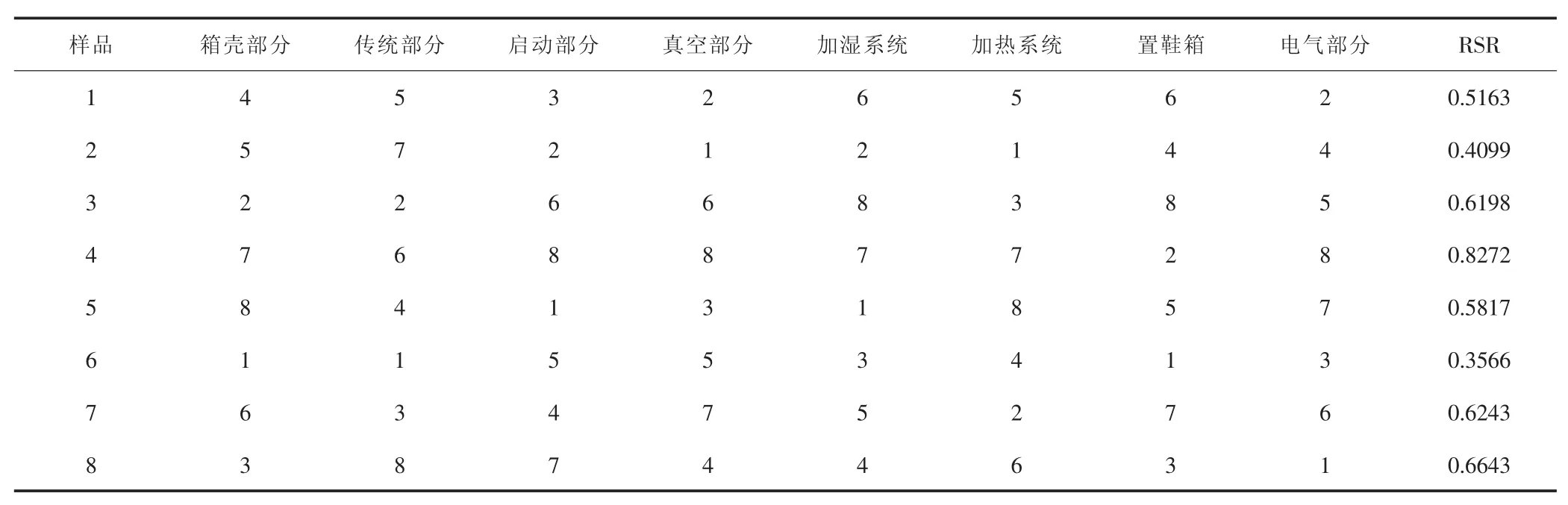
表6 评价真空湿热定型机属性的分布及秩和比

图1 真空湿热定型机评价结果

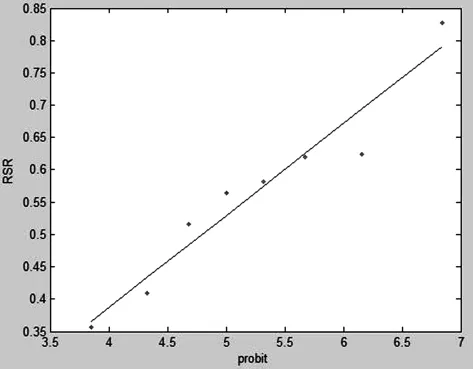
图2 一元线回归方程图

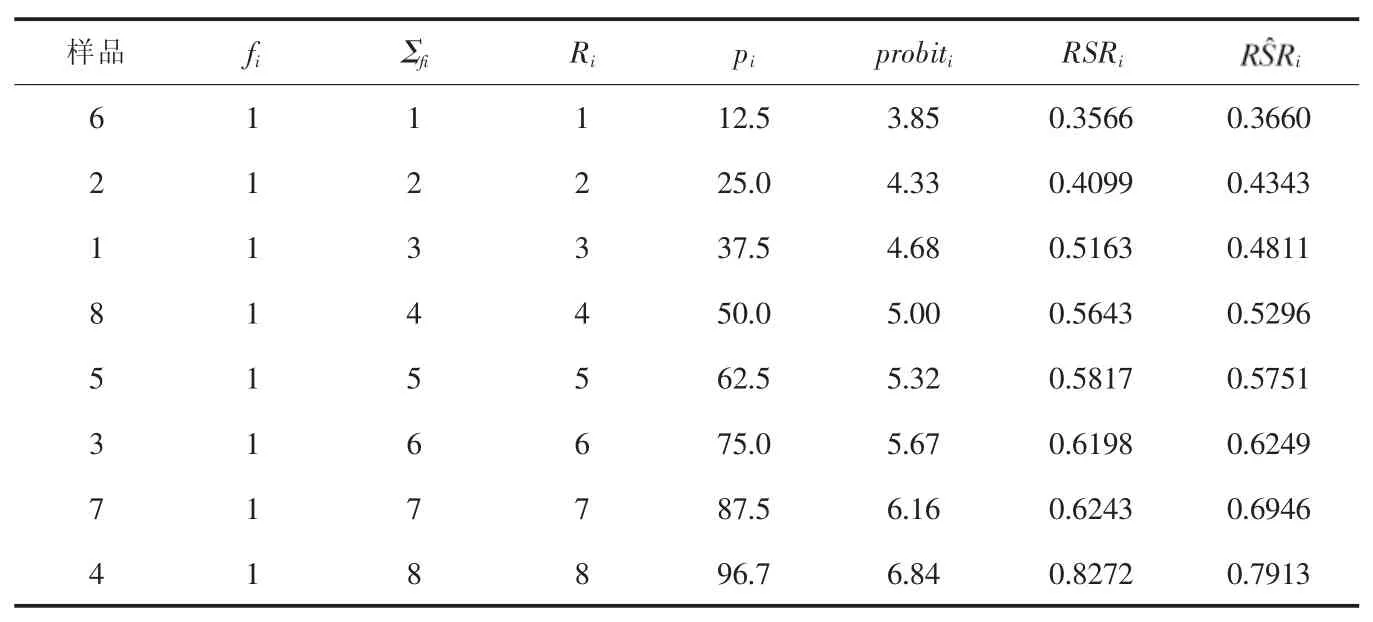
表7 评价的秩和比分布数据

表8 秩和比一元回归方程参数

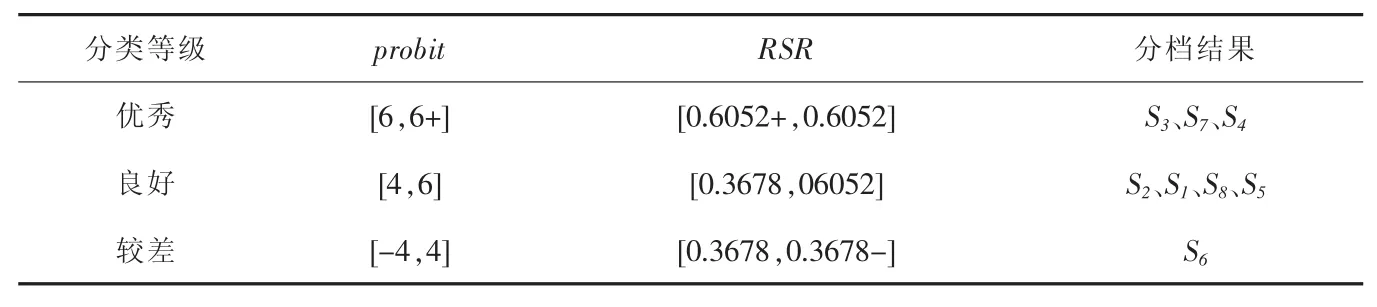
表9 真空湿热定型机分档情况

4 结语

真空湿热定型机是皮鞋生产的重要设备，它的性能和质量关系到制鞋工艺的成败和质量的优劣，客观评价真空湿热定型机的性能和质量，是保证选择优良设备和维持生产顺利进行的基础。秩和比法是一组全新的统计信息分析方法，是数量方法中一种广谱的方法，被广泛用于各领域的质量综合评价。秩和比法操作简便，对数据信息要求不高，既可以对评价对象进行排序，还可以对评价对进行分档，丰富了评价的内容，不仅能让人感受到直观的印象，还能让人挖掘出更多隐藏的深层信息，是多属性问题决策的有效工具。文中运用秩和比法对真空湿热定型机综合性能进行了评价，取得了良好的效果，模型有较高的相关性和显著性，能有效提高评价结果的可靠性。

[1]朱干江,王桂芝,赵靖.科技进步综合评价中秩和比法的运用[J].科技进步与对策,2007,24(6):51-54.

[2]付维华,付尧,李文帅.秩和比法(RSR 法)在环境污染健康损害中的应用 [J].广州化工,2012,40(3):101-103.

[3]陶庄.经典秩和比法详解[J].数理医药学杂志,2007,20(2):122-125.

[4]顾洁,王春义,牟宏.秩和比法在高压配电网项目评价中的应用 [J].电力科学与技术学报,2015,30(1):80-86.

[5]付学谦,陈皓勇.基于加权秩和比法的电能质量综合评价[J].电力自动化设备,2015,35(1):128-132.

[6]金晶,张研,刘文俊.基于加权秩和比法的麻城市乡镇卫生院服务能力综合评价[J].中国卫生事业管理,2016,(4):246-249.

[7]王天营.一元线性回归分析中三种检验的等价性研究[J].统计与决策,2011,(3):8-11.

[8]张敏静,刘雅娜,薛志群.一元线性回归方程有关检验问题的研究[J].价值工程,2012,(2):1-2.