基于CFD的涮爆烹饪过程模拟及试验验证

□ 崔 俊 黔东南民族职业技术学院 余冰妍 贵州大学酿酒与食品工程学院

肉类是传统烹饪过程最主要的食物材料[1]，在我国居民肉类消费中占主导地位，适合作为研究对象。涮爆是指以水为传热介质的烹饪过程，是家庭烹饪最常用的肉类食物制作方法之一[2]，其复杂性虽低于“爆”“炒”等烹饪工艺，但构建的传热控制方程经合理调整后可应用于“爆”“炒”等复杂烹饪工艺的模拟研究。

涮爆烹饪过程中，颗粒通过与传热介质对流换热获得热量，颗粒表面通过热传导将热量传递到颗粒中心，整个过程非稳态特征显著。采用传统物理测量方法难以获得颗粒全局温度历史，而颗粒全局温度变化又是掌握颗粒品质变化规律的重要参数[3]，因此有必要构建颗粒传热数学模型及求解方法，模拟涮爆过程颗粒传热过程从而获取颗粒温度分布，为烹饪品质研究提供基础参数。

涮爆过程中，搅拌频率影响液体-颗粒对流换热强度[4]，从而影响颗粒全局温度分布；颗粒传热学尺寸直接影响颗粒升温速率。因此，有必要对搅拌强度、颗粒传热学尺寸对涮爆过程颗粒全局温度分布的影响开展研究。

综上所述，需要基于理论传热学，开展涮爆过程颗粒的温度分布的研究，构建符合实际涮爆过程的颗粒传热数学模型及模型求解方法，把握烹饪的过程规律，获得基础数据。

1 材料与方法

1.1 理论基础

涮爆烹饪的过程特征是开放锅内被搅拌液体-食品颗粒的传热过过程，以水为传热介质的涮爆烹饪过程属于无内热源的非稳态传热。假设颗粒初始温度均匀，颗粒热物性质稳定，忽略颗粒收缩。

1.1.1 液体-颗粒非稳态传热数学模型

液体-颗粒非稳态传热控制方程可表述为：

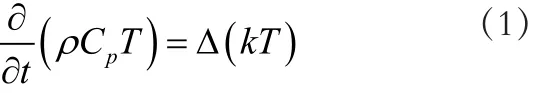
式（1）中，ρ为颗粒密度，单位为kg/m3；Cp为颗粒比热容，单位为J/（kg·℃）；T为颗粒温度，单位为℃；k为颗粒导热系数，单位为W/（ m·K）。

1.1.2 定界条件

初始条件：颗粒初始温度为环境温度 To。

边界条件：颗粒与传热介质——水通过对流换热传递热量，边界条件可表述为：

式（2）中，hfp为传热介质-颗粒对流换热系数，W/（ m2·K）；Tp为颗粒表面温度，℃；Tf为传热介质温度，℃。

1.1.3 数值计算

利 用COMSOL Multiphysics 有限元软件中的 Heat Transfer in Solids对式（1）、（2）进行数值求解。在 Geometry 中定义颗粒几何尺寸；Materials中定义颗粒热物性参数，在Temperature 和 Heat Flux 中分别加载初始条件和边界条件，见表1；利用Mesh进行网格划分，如图1所示；选用自动迭代求解器获得有限元解，并利用域探针获得颗粒不同空间位置的温度-时间曲线，并在后处理器中导出颗粒中心温度-时间曲线。

表1 猪里脊肉热物性参数[5-7]

图1 网格划分

1.2 试验原料

鲜猪里脊肉，市售。

1.3 仪器与设备

烹饪传热学及动力学数据采集分析系统，自研[8]；CY-20超级恒温水浴锅（上海博讯有限公司）；BL658切片机（深圳博莱电器有限公司）；21CK2105电磁炉（深圳美的电器制造有限公司）；家用平底锅（深圳美的电器制造有限公司）。

1.4 试验方法

1.4.1 原料处理

将原料猪里脊肉切分后置于-18 ℃冰箱中冷冻12 h，取出后用切片机将其切割为4 cm×4 cm×0.2 cm（长×宽×高）的肉片，采用半厚粘接法[9]将两片肉片粘接在一起，于0 ℃冰箱中冷藏，12 h后取出，恢复至室温。

1.4.2 颗粒中心点温度-时间采集

将热电偶插入到肉片中心，用镊子固定，将肉全部浸入水温为80 ℃的平底锅中加热并搅拌，以模拟实际涮爆过程中颗粒的运动，并用烹饪传热学及动力学数据采集分析系统采集肉片中心点的温度-时间变化曲线。

1.4.3 以最小温度目标总体差平方法（LSTD）验证模拟结果的可靠性

LSTD可反映数值模拟求得温度与实测时间温度的全程差异[10]，一般认为LSTD值小于5 %时，两组数据的差异可以接受，即模拟结果是可靠的，计算公式为：

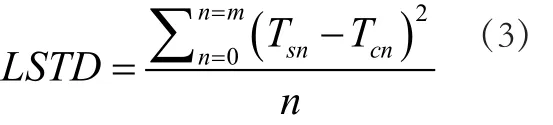
式（3）中：LSTD为温度差平方和；Tsn、Tcn分别为在共为m个的第n个时间点的模拟值与实测温度的关系。

1.5 数据处理

利用Origin 9对试验数据进行处理。

2 结果与分析

2.1 颗粒不同空间位置的温度变化

颗粒表面通过与传热介质对流换热获得能量，温度升温速率快；颗粒表面到颗粒中心，由于传热热阻的存在，颗粒中心升温速率慢于颗粒表面，如图2所示。

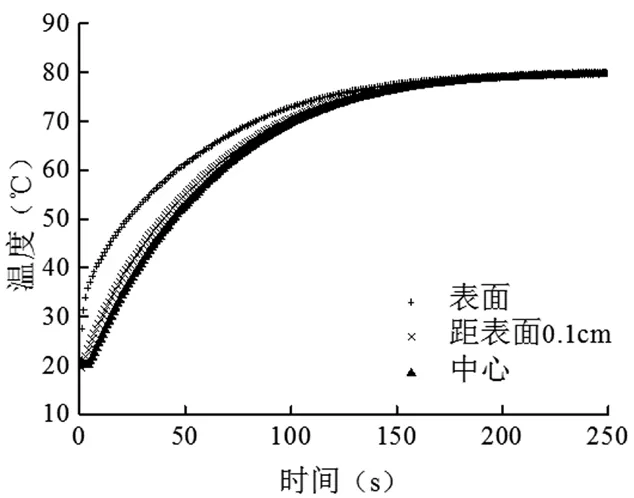
图2 200 W/（ m2·K ）时，颗粒（4 cm×4 cm×0.4 cm ）不同空间位置温度

2.2 不同搅拌强度对颗粒温度分布的影响

搅拌强度影响颗粒对流换热系数，搅拌强度越大则对流换热系数越大，颗粒在单位时间内与传热介质通过对流换热获得的热量多，则颗粒升温速率快，如图3所示。

2.3 不同几何尺寸对颗粒温度分布的影响

搅拌强度相同时，传热学尺寸越小，颗粒导热热阻越小，则颗粒单位时间获得的热量越多，颗粒升温速率越快，如图4所示。

图3 不同搅拌强度下颗粒(4 cm×4 cm×0.4 cm)中心点温度

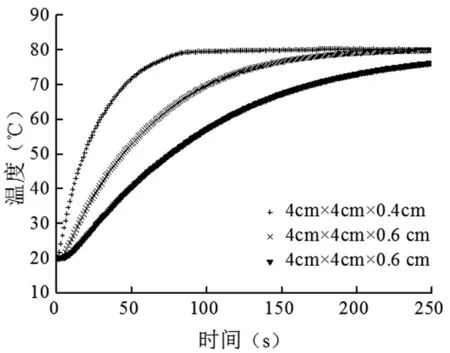
图4 200 W/（ m2·K）时，不同传热学尺寸颗粒的中心点温度

3 讨论

3.1 构建的颗粒传热数学模型的可靠性、代表性

进行数值模拟时，若传热学尺寸、物性参数、定界条件等与实际涮爆过程相同，由解的唯一性定律可知，数值模拟的结果是唯一的，若模拟值又与试验值吻合，则可证明模拟结果是可靠的[11，12]。通过对测定的实际涮爆过程颗粒中心温度曲线，与构建的颗粒传热数学模型模拟实际涮爆过程获得的颗粒中心温度曲线进行误差分析（如图5所示），LSTD值为0.11 %，证明了模型的可靠性。同时，构建的颗粒传热数学模型是理论模型，而非经验模型，可应用于不同涮爆操作条件下的温度模拟。

图5 200 W/（ m2·K)）时，颗粒（ 4 cm×4 cm×0.4 cm ）模拟中心温度与实测中心温度

4 结论

基于能量平衡，本文构建了涮爆过程中颗粒传热过程数学模型及模型求解方法，模拟了颗粒传热学尺寸、对流换热系数对颗粒温度分布的影响。模拟结果表明，颗粒传热学尺寸越小、对流换热系数越大，则颗粒升温速率越快。同时，利用热电偶采集实际涮爆过程中颗粒中心点的温度-时间曲线，与模拟求解出的温度-时间曲线进行误差分析，证明了模型的可靠性。最后，讨论了颗粒传热数学模型的代表性，数学模型经合理修正后可应用于其他烹饪工艺的模拟研究，是烹饪研究中获得颗粒全局温度历史的重要技术手段。

[1]刘合光,孙东升.中国猪肉消费现状与展望[J].农业展望,2010(1):35-38.

[2]王兰.烹饪原料学[M].南京:东南大学出版社,2007.

[3]邓力.中式烹饪热/质传递过程数学模型的构建[J].农业工程学报,2013(3):285-292.

[4]崔俊,邓力,汪孝,等. 油炒烹饪中食品体系吸热功率研究[J].食品工业,2017(7):182-187.

[5]天津轻工学院.无锡轻工学院.食品工艺学(上册)[M].北京:轻工出版社，1984:189-199.

[6]黄德龙.爆炒烹饪TTIs的构建及应用研究[D].贵阳:贵州大学,2016.

[7]李慧超. 计算流体动力学在食品热处理中的应用[D].贵阳:贵州大学,2016.

[8]邓力.基于时间温度积分器将手工烹饪转变为自动烹饪的方法[J].农业工程学报,2013(6):287-292.

[9]闫勇,邓力,何腊平,等.猪里脊肉烹饪终点成熟值的测定[J].农业工程学报, 2014(12):284-292.

[10]李玉振,郭成勋,王凤翼,等译.食品科学手册[M].北京:轻工业出版社, 1989: 282.

[11]陶文铨.数值传热学[M]. 第2版.西安:西安交通大学出版社,2001.

[12 ]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006.