排列与组合问题解法串烧

■河南省巩义二中 席文丽

排列与组合问题,历来是高中数学的难点,只要我们能掌握一些技巧与方法,就可以将排列与组合问题化难为易,化险为夷。

一、排列问题

例1 6人按下列要求站一排,分别有多少种不同的站法?

(1)甲不站在两端;(2)甲、乙必须相邻;(3)甲、乙不相邻;(4)甲、乙之间恰间隔2人。

分析:在与不在问题用直接法或间接法;相邻问题用捆绑法;不相邻问题用插空法。

解:(1)方法一:要使甲不站在两端,可先让甲在中间4个位置上任选1个,有种站法,然后其余5人在另外5个位置上全排列,有种站法,根据分步乘法计数原理,共有站法=480(种)。

方法二:若对甲没有限制条件,共有种站法,甲在两端共有2种站法,从总数中减去这两种情况的排列数即得所求的站法数为=480。

(2)方法一:先把甲、乙作为一个“整体”,看成一个人,有种站法,再把甲、乙进行全排列,有种站法,根据分步乘法计数原理,共有=240(种)站法。

方法二:先把甲、乙以外的4个人全排列,有A44种站法,再在5个空当中选出一个让甲、乙站,有种方法,最后让甲、乙作全排列,有A22种方法,共有=240(种)站法。

(3)方法一:(直接法)因为甲、乙不相邻,中间有空当,可用“插空法”,第一步先让甲、乙以外的4个人站队,有种站法;第二步再将甲、乙排在4人形成的5个空当(含两端)中,有种方法,故站法共有480(种)。

方法二:(间接法)6个人全排列有种站法,由(2)知甲、乙相邻有=240(种)站法,所以不相邻的站法有=720-240=480(种)。

(4)方法一:先让甲、乙以外的4个人全排列,有种方法,然后将甲、乙按条件插入站队,有种站法,故共有)=144(种)站法。

方法二:先从甲、乙以外的4个人中任选2人排在甲、乙之间的两个位置上,有种,然后把甲、乙以及中间2人看作一个“大”元素与余下2人全排列有种方法,最后对甲、乙进行排列,有种方法,故共有·=144(种)站法。

点评:求解排列问题的主要方法:(1)直接法,把符合条件的排列数直接列式计算;(2)优选法,优先安排特殊元素或特殊位置;(3)捆绑法,相邻问题捆绑处理,即可以把相邻元素看作一个整体与其他元素进行排列,同时注意捆绑元素的内部排列;(4)插空法,不相邻问题插空处理,即先把不受限制的元素进行排列,再将不相邻的元素插在前面元素排列形成的空中;(5)排除法,对于定序问题,可先不考虑顺序限制,排列后,再除以定元素的全排列;(6)间接法,正难则反,等价转化的方法。

二、组合问题

例2 某课外活动小组共13人,其中男生8人,女生5人,并且男生、女生各指定1名队长。现从中选5人主持某项活动,依下列条件各有多少种选法?

(1)只有1名女生;(2)2名队长当选;(3)至少有1名队长当选;(4)至多有2名女生当选;(5)既要有队长,又要有女生当选。

分析:按照特殊元素优先的方法逐一求解,注意“至少”、“至多”的含义。

(2)将2名队长作为一类,其他11人作为一类,故共有=165(种)选法。

(3)至少有1名队长含有两类:只有1名队长和2名队长。故共有=825(种)选法。

或用排除法,有=825(种)选法。

(4)至多有2名女生含有三类:有2名女生,只有1名女生,没有女生。故选法数为:

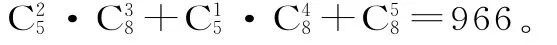
(5)分两类:

第一类女队长当选,结果为C412;

第二类女队长不当选,结果为C14C37+

故选法共有:=790(种)。

点评:组合中常见的两类题型的解法:

(1)“含”与“不含”的问题,“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取。

(2)“至少”、“至多”的问题,解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解。用直接法或间接法都可以求解。通常用直接法分类比较复杂时,可考虑逆向思维,用间接法处理。

三、分组分配问题

例3 (1)国家教育部为了发展贫困地区教育,在全国重点师范大学免费培养教育专业师范生,毕业后要分到相应的地区任教。现有6个免费培养的教育专业师范毕业生要平均分到3所学校去任教,有____种不同的分派方法。

(2)将6名教师分到3所中学任教,其中一所1名,一所2名,一所3名,则有____种不同的分法。

分析:(1)先确定平均分组的方法数,再把3组毕业生分到3所学校,最后由分步乘法计数原理求出方法总数。(2)先将6名教师分成3组(相当于3个不同元素),再将3个组分给3所中学,最后由分步乘法计数原理求分法总数。

解:(1)先把6个毕业生平均分成3组,种方法,再将3组毕业生分到3所学校,有种方法,故6个毕业生平均分到

(2)将6名教师分组,分三步完成:

第一步,在6名教师中任取1名作为一组,有种取法;

第二步,在余下的5名教师中任取2名作为一组,有种取法;

第三步,余下的3名教师作为一组,有

根据分步乘法计数原理,共有=60(种)取法。

再将这3组教师分配到3所中学,有=6(种)分法。

故共有60×6=360(种)不同的分法。

点评:(1)分组、分配问题的求解策略。

①分组问题属于“组合”问题,按组合问题求解,常见的分组问题有三种:

a.完全均匀分组,每组元素个数相等;

b.部分均匀分组,应注意不要重复,若有n组均匀,最后必须除以n!;

c.完全非均匀分组,这种分组不考虑重复现象。

②分配问题属于“排列”问题,可以按要求逐个分配,也可以分组后再分配。

(2)分组分配问题的解题方法。

①相同元素的“分配”问题,常用的方法是采用“挡板法”。

②不同元素的“分配”问题,利用分步计数原理,分两步完成,第一步是分组,第二步是发放。

③限制条件的分配问题采用分类法求解。