基于BP神经网络的改良黄土强度参数预测

江长通 王红肖 王银梅 朱雪芳

摘要：选用新型固化材料SH改良黄土，以室内土工试验数据为学习样本和测试样本，通过BP神经网络模型就含水率对改良黄土力学参数的影响进行了预测分析，结果表明：隐含层函数为正切tansig函数、输出层为对数logsig函数、隐含层神经元数为9时训练次数最少，模型误差最小；根据试验数据建立了非线性预测模型，预测结果与试验数值基本吻合，内摩擦角的平均误差为0.5%，黏聚力的平均误差为7.74%，内摩擦角的预测效果优于黏聚力的，但整体误差较小，且都在土工试验允许误差范围内，可见将BP神经网络应用到力学参数的预测中是合理的。

关键词：固化剂；BP神经网络；力学参数；黄土

中图分类号：TU444 文献标志码：A doi：10.3969/i.issn.1000-1379.2018.01.027

黄土的高壓缩性、湿陷性、强度低等不良工程特性，使得其必须经处理后才能满足高速公路、铁路路基和水利工程坝基等的设计要求。工程上常见的黄土处理方式有换填、打桩、加入固化材料等，新型固化剂因性能优良而被广泛应用于基础工程中。鉴于此，国内外学者开发研制了一系列固化材料。1994年，Bell[1]在水泥和石灰中加入PFA添加剂，使改良土强度明显提高；樊恒辉等[2]研究了MBER固化剂掺量、含水率、龄期和养护环境等因素对陕西杨凌粉质黏土强度的影响；王银梅等[3]研究表明，将黄土与新型高分子材料SH拌和后，土体内部结构发生了变化，土体强度明显增强。

常见的土体力学性质指标一般是通过室内试验测得的。通过直接剪切试验、固结排水三轴试验、固结不排水三轴试验等可以获得土体的抗剪强度参数，但是繁杂、重复的试验受仪器设备、试验环境、人为误差等因素影响，而且对于多水平、多指标试验或者新材料，用传统的回归方法很难掌握其规律，所以建立一种智能网络模型成为现阶段的发展趋势。BP神经网络忽略了试验仪器和操作等方面的误差，无需建立复杂的模型及函数关系即可实现土体参数的非线性映射。通常情况下，含水率对边坡的稳定性影响较大，因此以控制含水率为目的进行土体物理力学性质试验显得颇为重要。为了研究含水率对改良黄土强度参数的影响程度及改良固化材料的使用要求，一方面，要进行大量繁杂的试验才能得到土体强度参数范围，过程中需要消耗大量的人力、物力、财力等，造成了很大程度的资源浪费；另一方面，改良土料中含水率对土体强度参数的影响很难形成较规律的序列。因此，建立BP神经网络模型对改良黄土不同含水率下的内摩擦角和黏聚力进行预测，以代表性含水率5%、10%、15%、20%、25%进行内摩擦角和黏聚力的预测示例。

1 土样及固化剂的选取及其改良原理

1.1 试验材料及试验方法

试验将山西太原黄土、兰州大学制备的固化剂SH和湖南省益佳石灰厂生产的二级石灰作为试验材料，黄土物理性质见表1。按预设的比例分别在黄土中加人不同掺量的石灰，拌和均匀后加入SH及水，混合土样需在密闭容器内充分接触12h。将拌和均匀的土样分3次装人直径40mm、高80mm的模具内，手工压实制备土样，脱模。试样制备完成后置于自然条件下风干。最后选取STWCY-1型无侧限压力仪进行无侧限抗压强度试验。

1.2 固化剂的改良原理

SH含聚乙烯醇等成分，质量分数为5%，密度为1.27～1.31g/cm3，可无限稀释；无毒无刺激性；常温下即可加固，具有高效性、持久性。SH对沙、土颗粒有包裹、填充和胶结的作用[4]。高分子链上的-COOH、-OH等基团的氢离子与黄土颗粒表面的金属阳离子发生离子交换，增大了黄土颗粒之间的吸引力，使得颗粒之间结合更加紧密；高分子链上的-COOH、-OH等与土粒上的羟基能够形成氢键，氢键可以使分子间结合更加稳定、牢靠，使得土体更加稳固；固化剂SH上的亲水基能与土粒结合，而憎水基则处于暴露状态，土体的亲水性大幅度减弱，使得水分子破坏土体结构变得更加困难。除此之外，固化剂SH是高分子材料，当与土粒作用时会使整个土体结合成整体性的三维网状结构，达到很好的改良黄土的目的。

2 BP神经网络模型

2.1 模型的建立

影响改良黄土内摩擦角和黏聚力的主要因素有固化剂SH掺量、干密度、含水率等，而大量试验研究证明含水率对土体强度影响较大，因此以SH改良黄土的含水率为输入层，以内摩擦角φ和黏聚力C为输出层建立BP神经网络模型。

通过模拟分析现有的不同含水率对应试验测得的C、φ值的22组数据，得到改良黄土含水率与强度参数内摩擦角和黏聚力的内在非线性关系。对原始数据进行归一化处理后可以减少学习时间，加快收敛速度，进而提高预测精度，因此在样本学习之前，先对原始数据进行归一化处理。式中：Pi为土体强度归一化后的数值，i为试验数据序号；xi为固化剂掺量、干密度、风干时间一定时，无侧限抗压强度的数值；xmaxi、xmini分别为固化剂掺量、干密度、风干时间一定时，无侧限抗压强度的最大值和最小值。

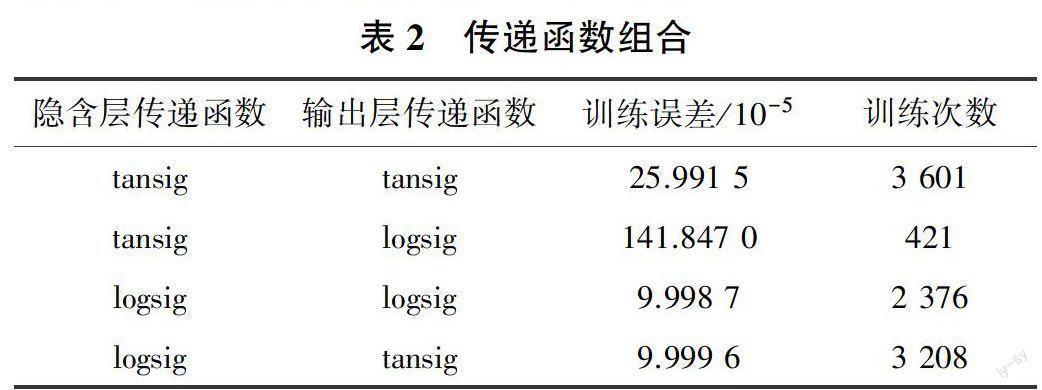
数值归一化后建立模型。经过反复学习分析后，传递函数选择正切函数tansig及对数函数logsig。训练结果见表2。由表2可知，SH与石灰组合隐含层采用tansig函数、输出层采用logsig函数，此时训练次数最少，训练误差也满足土工试验要求。

2.2 归一化及反归一化数据整理

利用反归一化公式将预测结果还原为无侧限抗压强度：式中Xi为反归一化后的无侧限抗压强度。

预测模型中输入节点和输出节点的个数需根据工程的复杂程度确定，刘勇健等[5]发现适当增加隐含层层数，能增强网络解决问题的能力。根据经验公式Y=2P+1[6]（Y为隐含层神经元数，P为输入层上的神经元数）可以求得隐含层神经元数。隐含层神经元数定为3、5、7、9，经过训练后发现隐含层神经元数为9时，误差较小，学习时间较短，网络的性能最好。不同隐含层神经元数的反归一化土体强度参数误差曲线见图1、图2。

从图1、图2可以看出，当隐含层神经元数为3时，归一化后的黏聚力和内摩擦角误差均最大，尤其是黏聚力，最大误差可达175%。随着模型隐含层神经元数的增加，内摩擦角与黏聚力的误差均呈减小趋势，当隐含层神经元数为9时，内摩擦角误差为0.03%～2.19%，平均误差为0.5%；黏聚力的误差为0.11%～23.87%，平均误差为7.74%，误差最小，且收敛较快，故隐含层神经元数取9是合理的。由此还可以看出，基于试验结果建立的BP神经网络模型预测改良黄土的黏聚力和内摩擦角是可行的。

从图1、圖2还可以看出，内摩擦角的预测效果要比黏聚力的好。其原因一方面可能是试验数据问题，SH改良黄土强度参数中内摩擦角的规律性较强，在预测过程中，内摩擦角首先完成传递函数的实时学习及传递过程，而黏聚力则需要考虑内摩擦角的学习过程，再综合自身特点完成BP神经网络函数的学习传递，故内摩擦角的精确度更高；另一方面，含水率与SH改良黄土强度参数内摩擦角的相关性较强，水是润滑剂，水对内摩擦角的影响主要是使颗粒间滑动的相对阻力减小，而含水率对黏聚力的影响主要与水膜的厚度及大小有关，而水膜的厚度和大小不可能无限度增加，因此在只考虑含水率对直剪强度参数的影响时，内摩擦角的误差更小。

3 预测示例

根据前面试验数据建立的预测模型，可以实现从物理参数含水率到力学参数内摩擦角及黏聚力的转变。含水率分别为5%、10%、15%、20%、25%时的内摩擦角和黏聚力预测值见表3。

4 结论

以物理参数含水率为输入变量，力学参数内摩擦角和黏聚力为输出变量，建立了关于含水率与土体力学参数内摩擦角和黏聚力的BP神经网络预测模型。模型训练发现，隐含层函数为正切tansig函数、输出层为对数logsig函数、隐含层神经元数为9时训练次数最少，模型误差最小。根据试验数据建立了非线性预测模型，预测结果与试验数值基本吻合，内摩擦角的平均误差为0.5%，黏聚力的平均误差为7.74%，内摩擦角的预测效果优于黏聚力的，但整体误差较小，且都在土工试验允许误差范围内。可见，将BP神经网络应用到力学参数的预测中是合理的。通过强度参数的预测，为后续改良黄土强度试验、冻融及干湿循环等试验指标的获取提供了一种科学的方法，从而可以在不考虑人为因素、环境误差等情况下准确地进行模型预测。

综上，强度试验的结果与BP神经网络的预测数值基本吻合，表明该神经网络模型具有较高的预测精度。由此可见，将BP神经网络应用到土体强度参数预测中是可行的，因此可以尝试建立固化剂改良土体的抗剪强度、冻融循环强度等指标的计算模型，从而提供了一种在不考虑人为、环境等因素影响下进行固化剂改良土体强度参数研究的新思路。

参考文献：

[1]BELL F G.An Assessment of Cement-PFA and Lime-PFAUsed to Stabilize Clay-Size Materials[1].Bulletin of the In-ternational Association of Engineering Geology，1994，49（1）：25-32.

[2]樊恒辉，吴普特，高建恩，等.固化土集流面无侧限抗压强度影响因素研究[J].农业工程学报，2006，22（9）：11-15.

[3]王银梅，杨重存，湛文武，等.新型高分子材料SH加固黄土强度及机理探讨[J].岩石力学与工程学报，2005，24（14）：2554-2559.

[4]王银梅，湛文武，韩文峰.SH固沙机理的微观探讨[J].岩土力学，2005，26（4）：650-654.

[5]刘勇健，沈军，刘义健.人工神经网络在水泥加固土力学性能预测中的应用[J].岩土力学，2001，22（3）；330-333.

[6]赵振宇，徐用憋.模糊理论和神经网络的基础与应用[M].北京：清华大学出版社，1996；23-24.