基于梯度信息的自适应邻域噪声图像分割模型
李 钢,李海芳,尚方信,郭 浩
(太原理工大学 计算机科学与技术学院,太原 030024)
0 概述
图像分割一直是图像处理领域的热点和难点,其主要目标是将图像划分为若干个不重叠的子区域,每一区域内具有相同的特征。由于图像内容种类繁杂、特征不统一且易被噪声污染,因此目前没有一种通用的分割方法可取得较稳定可靠的效果。文献[1]提出活动轮廓模型,该模型与多种统计方法相结合,在解决各种类型图像的分割问题中得到了较为广泛且成功的应用,但其仍存在诸多问题。
针对上述问题,本文基于传统的噪声鲁棒分割算法和图像梯度信息,构建一种可变形自适应邻域的活动轮廓模型,目的是在兼顾算法效率的同时,提高叠加概率噪声的非同质或弱边缘图像分割精度。
1 研究背景
活动轮廓模型按分割依据的不同可分为边缘型活动轮廓模型[2]和区域型活动轮廓模型[3-5]。以测地线活动轮廓(Geodesic Active Contours,GAC)模型[2]为代表的边缘型模型仅能处理具有明显边界的无噪声简单图像,以C-V模型[6]为代表的区域型活动轮廓模型使用分片常数函数拟合图像的背景和目标区域,提取目标边缘并进行图像分割,该模型对初始轮廓位置具有鲁棒性,但其仅能分割同质均匀图像。针对C-V模型的不足,以局部二值拟合(Local Binary Fitting,LBF)模型[7]和局部图像拟合(Local Image Fitting,LIF)模型[8]为代表的局部区域活动轮廓模型利用图像局部信息进行分割,可较准确地分割灰度不均匀的图像。但上述局部模型的能量函数是非凸的,在水平集演化过程中容易陷入局部极小值,且对轮廓初始位置敏感性较强。
很多学者在LBF、LIF的基础上提出改进模型,文献[9]将方差统计量引入LBF模型,通过分析每个像素邻域的灰度分布和图像局部高斯概率进行图像分割,其进一步增强了局部区域活动轮廓模型对非均质图像的适应能力,但依然不能准确分割弱边界性质显著的图像和噪声图像。文献[10]提出的LCK(Local Correntropy-based K-means)模型使用局部相关系数判别正常像素点与噪声点,并适当降低噪声点在运算过程中的权重以保证能量函数不被噪声干扰,对极值噪声(如椒盐噪声)具有较好的分辨能力,但该模型在强噪声环境下会抛弃过多图像信息,且不能准确分辨没有显著极值的概率噪声(如高斯噪声)。文献[11]提出的模糊C聚类(Fuzzy C-Means,FCM)方法认为像素点应当对各分割子区域均具有从属概率,不应绝对地属于一个分割子区域。该方法可较准确地分割椒盐噪声图像,但其像素点以概率形式从属于多个子区域,在高斯噪声和弱边界图像目标边缘处易造成混淆从而导致分割失败。文献[12]提出一种邻域自适应LCV模型,该模型认为图像均匀程度应与邻域半径负相关,其根据图像局部灰度均值差异判断图像均匀程度,并自动选择邻域半径。LCV模型较好地兼顾了算法性能和分割精度,可较准确地分割非均质图像和背景区域较复杂的图像,但该模型只考虑了邻域在分割曲线两侧的灰度均值差异,无法准确分割灰度均值变化不显著的概率噪声图像。
上述模型都只考虑了像素灰度值与局部均值的差异,对图像全局和局部空间内灰度值的变化情况考虑不足,无法准确分割具有弱边界的概率噪声图像,且都容易陷入局部极小值。针对该问题,本文构建一种可变形的自适应邻域分割模型,使用图像梯度方向和长度引导邻域变形,在图像梯度值较大时,模型认为此处具有清晰的目标边界,邻域沿梯度方向变形,使目标边界两侧有更多有效信息参与计算;在图像梯度值较小时,模型认为此处是平滑区域或具有弱目标边界,邻域形态接近圆形,避免抛弃过多有价值的图像信息。
2 相关理论
LCK是一种噪声鲁棒的分割模型,其创新点在于引入一种基于K-means聚类方法的相关性系数,用于衡量邻域内像素点与邻域中心的相似程度。该相关性系数的值介于0和1之间,某一像素点处的相关性系数越接近0,说明该像素点与邻域内图像内容的相关性越低,被噪声污染的可能性越大。
被椒盐噪声污染的像素点往往与其邻域内灰度均值相差较大,其具有较小的相关性系数。LCK模型的能量函数在计算中受噪声点影响较小,因此,该模型对椒盐噪声图像具有较好的鲁棒性。LCK模型的能量函数表示为:
(1)
其中,惩罚项P(φ)使水平集函数在迭代过程中保持为符号距离函数[13],而无需重新初始化,L(φ)为曲线长度约束项,用来确保分割曲线在演化过程中保持平滑。P(φ)、L(φ)的形式如式(2)、式(3)所示。
(2)
(3)
定义在整个图像域Ω上的水平集函数φ的梯度值φ恒为1时,惩罚项P(φ)的值最小。此时以零水平集为起点,在图像域上任一方向每移动一个单位长度,函数值的变化量为1,即函数φ符合“符号距离函数”的定义。长度约束项L(φ)在曲线长度为0时取得最小值,对分割轮廓曲线起到类似气球弹力的约束作用。图像拟合项要求图像灰度值与邻域均值尽可能地接近。因此,在能量函数式(1)最小化的过程中,φ趋近于1,在图像拟合项和长度约束项共同作用使分割轮廓尽可能接近目标边界的同时,去除轮廓上多余的不平滑部分。

(4)
其中,I为图像灰度值,μ1、μ2为图像内各点附近的局部灰度均值,表达式如下:
(5)
(6)
其中,wx,y为图像域内x、y2点间的相关性系数,表达式为:
wx,y=Hε(φ)g(‖I(y)-μ1(x)‖2)+
(1-Hε(φ))g(‖I(y)-μ2(x)‖2)
(7)
(8)
该方法通过计算图像中各像素点的灰度值与其邻域灰度的相关性,减少水平集函数迭代过程中噪声点对分割结果的影响,但由于该模型通过降低权重的方法处理噪声点,在图像包含较多噪声时可能会抛弃过多图像内容,从而出现分割失败的情况。
3 本文模型
传统的噪声鲁棒模型致力于减少噪声点对能量函数的干扰,如利用图像全局或局部的灰度统计特征判定噪声点,该类模型使算法在噪声环境下依然可以得到较为准确的分割结果,在处理灰度变化显著的椒盐噪声时效果显著,但对高斯噪声适应能力较弱,原因是被高斯噪声污染的像素点与原图差别不大,传统的噪声鲁棒模型无法准确分辨噪声点。
以高斯噪声为代表的概率分布噪声具有良好的统计学性质,当噪声服从的分布均值为0时,整幅图像灰度均值与原图十分接近。考虑到C-V模型是LBF模型在邻域范围与图像尺寸相同时的特殊形式,可以知道分割模型的邻域范围越大,计算邻域均值时考虑的像素点越多,高斯噪声点对分割结果的影响越小,但过大的邻域范围将导致局部模型失去对非均质图像的适应能力。文献[14]讨论邻域半径的作用,指出邻域半径大小直接影响局部模型的分割精度和曲线演化速度。因此,本文在LCK模型的基础上,考虑图像梯度信息并设定更丰富的邻域形态,通过图像内各点的灰度梯度值和梯度方向引导邻域变形,该方法不仅在计算邻域均值时使尽可能多的图像信息参与运算,提高概率噪声的鲁棒性,而且避免邻域范围过大对模型处理弱边界图像时起到的负面作用,从而提高分割精度。进一步地,引入局部相关性系数,考虑邻域内一点与其他像素点的相关程度,避免邻域变形过程中由抛弃过多图像信息导致的噪声信息干扰分割结果的问题。
如图1所示,高斯噪声图像的梯度值变化较小,保留了大部分梯度信息。叠加少量椒盐噪声的图像虽然不影响肉眼观察,但噪声点附近具有显著的灰度变化。传统的噪声鲁棒模型通过像素点与其附近灰度均值的差异程度分辨椒盐噪声点,但无法分辨高斯噪声点。本文方法使用图像梯度方向和长度信息引导邻域变形,不依赖邻域在分割曲线两侧的灰度均值,弥补了自适应LCV模型的不足。当图像出现显著灰度变化、梯度值较大时,本文模型认为此处是目标边界的可能性较大,邻域形状变为椭圆;当图像局部近似均匀、梯度值较小时,椭圆偏心率变小,邻域近似为圆形。

图1 噪声图像的梯度值对比
如图2所示,在一幅目标为白色(灰度值较大)、背景为灰色(灰度值较小)的二值图像中取4个具有代表性的局部区域,点x位于背景或目标区域内部时,图像梯度值较小,邻域形状接近圆形;点x位于目标与背景区域交界处时,图像梯度值较大且具有显著的方向,此时邻域形状变为长轴方向与梯度方向一致的椭圆,椭圆偏心率与图像梯度值正相关。

图2 本文模型邻域变形示意图
本文模型核函数定义如下:
(9)
(10)

模型能量函数构造如下:
(11)


(12)
其中,等号右侧前后2项分别是邻域内外2侧的图像拟合项,λ1、λ2是相应的权重系数,c1(x)、c2(x)表示以点x为中心的邻域灰度均值。根据变分法和Euler-Lagrange方程,本文模型的水平集演化方程如下:
(13)
(14)
其中:
(15)
(16)
R(x)为点x间的相关性系数,表达式为:
(1-Hε(φ))g(‖I(y)-c2(x)‖2)dy
(17)
运用本文模型对图像进行分割的主要步骤如下:
1)计算图像梯度向量的方向和大小;
2)初始化水平集函数φ;
3)初始化相关性系数Ri(x)为一个与图像大小相同的零矩阵;
4)根据式(15)、式(16)计算c1(x)、c2(x);
5)根据式(13)、式(14)演化水平集函数;
6)根据式(17)计算Ri+1(x),Ri(x):=Ri+1(x),判断其是否满足迭代停止条件,如果满足,停止曲线演化;否则,重复步骤4)~步骤6)。
4 实验结果与分析
为验证本文模型对弱边界图像及噪声图像的处理能力,将本文模型、LBF模型、邻域自适应LCV模型、LCK模型、RLSF模型和FCM模型的分割结果进行对比。实验均在Lenovo台式机上使用MATLAB R2017a完成。如无特殊说明,本文实验参数设置为:λ1=1,λ2=1,μ=0.003×255×255,ν=1,Δt=0.1,ε=1,m=1,n=1。
4.1 合成图像实验
本节实验选取5幅具有代表性的人工合成图像,分别对其叠加等强度的高斯噪声,然后将本文模型与其他5种活动轮廓模型的分割结果进行对比分析。为便于统计分析,数据集图片分辨率均被调整为256像素×256像素,应用骰子相似系数法(DSC)[15]和分割错误比(RSE)与手工标注分割结果进行定量比较。DSC与RSE定义如下:
(18)
(19)
其中,Area(S)表示S区域的面积,也即包含的像素个数,S1,S2分别表示模型分割结果与基准分割结果中的前景目标区域。实验结果中,DSC值越接近1,RSE值越接近0,则模型分割结果越接近基准分割结果,模型分割精度越高。
图3所示为6种模型对部分弱边界图像和高斯噪声图像的分割结果。其中,弱边界图像与分割结果展示于奇数行(A1、B1、C1、D1、E1),对应的噪声图像与分割结果展示于偶数行(A2、B2、C2、D2、E2)。为确保对比实验的有效性和公平性,初始轮廓均位于图像中心,且设定相同的分割参数。

图3 6种模型对合成图像的分割结果
通过观察图3可以发现,所有模型均可以有效处理具有清晰边界的人工图像A1;LBF模型、LCK模型和RLSF模型在分割具有模糊边界的人工图像B1、C1时失效,这是由于该3个模型的卷积核尺寸是固定值,不能根据图像内容自动调整,在分割轮廓外侧是面积较大的均匀区域的图像时,模型会使能量泛函陷入局部极小值,从而导致分割失败,但自适应LCV模型和本文模型弥补了这一缺陷。同时,对于图像中包含多种弱边界目标且相距较近的D1,尺寸固定的邻域使LBF模型和LCK模型能对其进行准确分割;自适应LCV模型和本文模型在局部灰度值变化明显时,可以自动缩小邻域范围,因此,分割下侧白色目标时不受上侧黑色目标的影响。在同时具有光照不均匀、灰度不均匀和弱边界性质的图像E1上,自适应LCV模型无法进行准确分割,原因是图像中目标边界处灰度变化不显著,模型在局部使用的邻域面积过大,考虑的图像信息过多,导致分割失败;FCM模型对高斯噪声的适应能力优于自适应LCV模型,但FCM模型模糊聚类的特性使得在图像噪声密度较大时像素点被正确分类的概率不大,从而出现误分割现象。值得注意的是,FCM模型在处理噪声弱边界图像时,其模糊聚类机制更容易被干扰从而出现误分割现象。本文模型考虑了图像梯度信息,因此,其可以抛弃部分不重要的图像信息,最终进行准确分割。
叠加高斯噪声实验图片的分割结果验证了本文模型具有较好的抗噪声能力,LBF模型、LCK模型、RLSF模型、自适应LCV模型和FCM模型均表现不佳,原因是高斯噪声点附近不具有类似椒盐噪声的显著灰度变化,LCK模型的相关性系数方法无法准确分辨正常像素点和噪声点,未使用高斯核函数的自适应LCV模型也由于灰度变化不显著而无法准确选择邻域尺寸,导致分割失败,而被高斯噪声污染的图片梯度值与原图接近,因此,本文模型可以得到与无噪声图片相接近的分割结果。
本节实验各模型分割结果的DSC值、RSE值如表1、图4和图5所示。由实验结果可以看出,与其他模型相比,本文模型可在弱边界图像、高斯噪声图像上进行准确且稳定的分割。
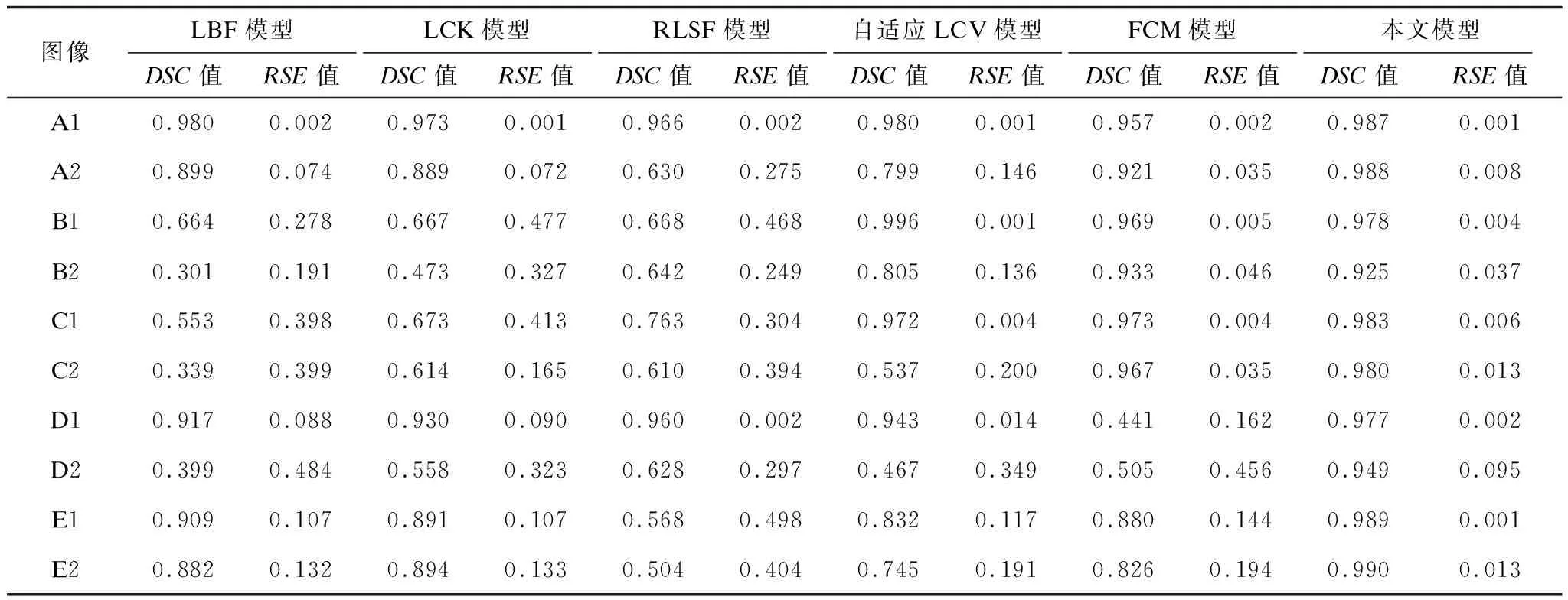
表1 6种分割模型在合成图像上的DSC值和RSE值

图4 合成图像分割结果DSC值折线图

图5 合成图像分割结果RSE值折线图
4.2 自然图像实验
在弱边界噪声合成图像上进行的对比实验证明了本文模型对该类型图像分割的有效性,为证明本文模型在分割图像时具有广泛的适应性,本节实验引入Cornell大学iCoseg自然图像数据集[16],并对其中每幅图片都进行散焦模糊并叠加方差为 0.2的高斯噪声,使用与上节实验相同的量化方法评估各模型的分割性能。图6所示为LBF模型、LCK模型、RLSF模型、自适应LCV模型、FCM模型和本文模型在散焦的噪声自然图像数据集上的分割结果。

图6 6种模型对自然图像的分割结果
由图6的实验结果可以看出,采用固定尺寸卷积核的LBF模型、LCK模型受到弱边界性质和高斯噪声的影响,无法根据图像性质和灰度分布规律自动地调整邻域大小,LCK模型的相关性系数方法无法准确辨别高斯噪声点,因此,这2个模型极易陷入局部极小值从而出现过分割或误分割的情况。RLSF模型未使用高斯核函数,较小的迭代步长使模型对弱边界和非均值图像具有较好的适应能力,但致使模型容易被高斯噪声干扰,从而陷入局部极小值,最终在全图像域上出现误分割。自适应LCV模型依据邻域两侧局部灰度均值的差异调整邻域大小,无法在弱边界和高斯噪声条件下适应内容和纹理较复杂的自然图像,同时由于没有使用高斯核函数,因此易出现全局性质的误分割。FCM模型的模糊聚类方法无法在天空、水面等具有相对均匀但具有纹理的噪声区域分辨噪声点,易出现误分割现象。本文模型根据图像梯度引导邻域变形,对高斯噪声和自然图像的背景或目标区域内的干扰信息不敏感,从而获得理想且稳定的分割结果。上述分割结果的DSC值、RSE值量化对比结果如表2、图7和图8所示。
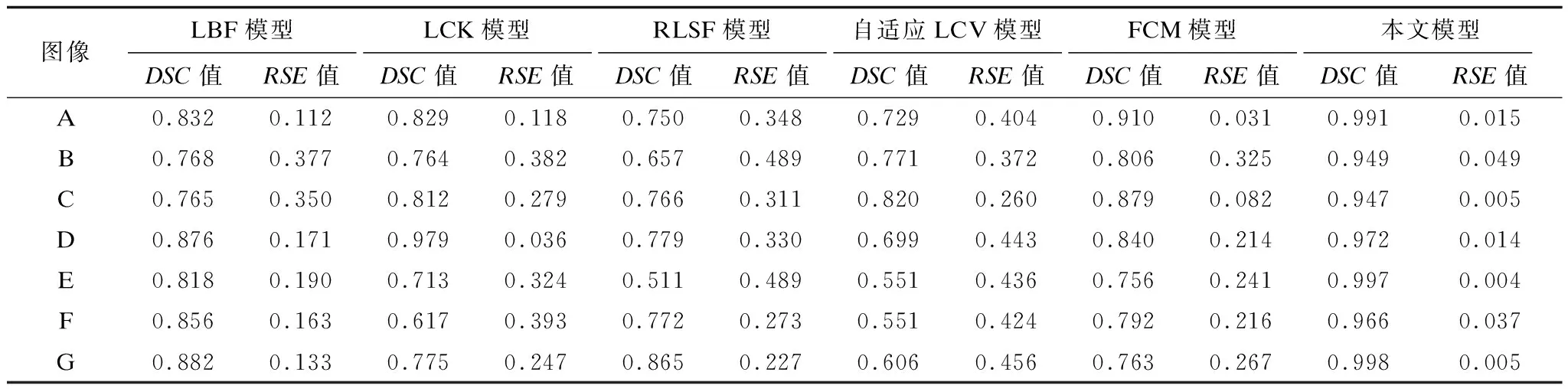
表2 6种分割模型在自然图像上的DSC值和RSE值

图7 自然图像分割结果DSC值折线图

图8 自然图像分割结果RSE值折线图
4.3 初始轮廓敏感性实验
为验证本文模型对初始轮廓位置的弱敏感性,本节实验在多幅人工合成噪声图像上设置5种初始轮廓位置,分别位于图像的四角和中部,本文模型对其的分割结果如图9所示。

图9 本文模型在不同初始轮廓下的分割结果
由图9可以看出,初始轮廓与待分割目标轮廓的拓扑关系对最终分割结果的影响不显著,即无论初始轮廓是否与目标轮廓存在交叉重叠关系,模型在噪声环境下均可进行准确分割,且分割结果具有稳定性和一致性。本文模型使用图像梯度信息引导邻域变形,允许真正包含目标边界信息的像素点参与计算,且抛弃掉少量无关的像素信息,因此,其对初始轮廓具有较好的鲁棒性。
5 结束语
本文构建一种基于图像梯度信息的邻域自适应分割模型,由于基于图像梯度建立邻域变形机制,目标边界较清晰,因此与自适应LCV模型、LCK模型和FCM模型相比,该模型可以准确分割高斯噪声图像,且在图像具有弱边界和非均质性质时依然可以保持良好的有效性和分割精度。本文模型引入了新的模型参数,实现参数设置自动化将是下一步着力解决的问题。
[1] KASS M,WITKIN A P,TERZOPOULOS D,et al.Snakes:active contour models[J].International Journal of Computer Vision,1988,1(4):321-331.
[2] CASELLES V,KIMMEL R,SAPIRO G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[3] 陈 雷.基于活动轮廓模型的图像分割算法研究[D].济南:山东大学,2013.
[4] 李 磊.图像分割研究现状概述[J].信息技术与信息化,2015(3):85-87.
[5] MUMFORD D,SHAH J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics,1989,42(5):577-685.
[6] CHAN T F,VESE L A.Active contour without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.
[7] LI C,KAO C Y,GORE J C,et al.Implicit active contours driven by local binary fitting energy[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2007:1-7.
[8] ZHANG K,SONG H,ZHANG L.Active contours driven by local image fitting energy[J].Pattern Recognition,2010,43(4):1199-1206.
[9] WANG L,HE L,MISHRA A,et al.Active contours driven by local Gaussian distribution fitting energy[J].Signal Processing,2009,89(12):2435-2447.
[10] WANG L,PAN C.Robust level set image segmentation via a local correntropy-based K-means clustering[J].Pattern Recognition,2014,47(5):1917-1925.
[11] JIANG X L,WANG Q,HE B,et al.Robust level set image segmentation algorithm using local correntropy-based fuzzyc-means clustering with spatial constraints[J].Neurocomputing,2016,207(C):22-35.
[12] 廖祥云,袁志勇,郑 奇,等.引入局部全局信息的区域自适应局域化快速活动轮廓模型[J].计算机学报,2016,39(7):1464-1476.
[13] LI C,XU C,GUI C,et al.Level set evolution without re-initialization:a new variational formulation[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2005:430-436.
[14] LIAO X,YUAN Z,ZHENG Q,et al.Multi-scale and shape constrained localized region-based active contour segmentation of uterine fibroid ultrasound images in HIFU therapy[J].PLOS One,2014,9(7).
[15] DIETENBECK T,ALESSANDRINI M,FRIBOULET D,et al.Creaseg:a free software for the evaluation of image segmentation algorithms based on level-set[C]//Proceedings of IEEE International Conference on Image Processing.Washington D.C.,USA:IEEE Press,2010:665-668.
[16] BRATRA D,KOWDLE A,PARIKH D,et al.iCoseg:interactive cosegmentation by touch[EB/OL].[2017-09-25].http://chenlab.ece.cornell.edu/projects/touch-coseg /index.html.

