地震作用对有砟轨道桥上无缝道岔纵向受力与变形影响分析

罗华朋，陈 嵘，宋姣姣，王 平

(1.广州地铁设计研究院有限公司，广州 510010；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；3.同济大学道路与交通工程教育部重点实验室，上海 201804)

随着我国高速铁路特别是西部铁路建设的推进，线路遭遇地震灾害时有发生[1-4]，多次出现地震作用下桥梁结构无明显破坏而其上轨道结构发生屈曲、失稳等现象。造成地震作用下桥上无缝线路失稳的主要原因有轨条内存在较大且不均匀分布的纵向力，线路不平顺弯曲以及道床松动等。由于桥上无缝道岔结构受力、变形传递机理复杂[5-9]，部件组成较多，强度、稳定性和相对位移均不易控制，因此有必要研究地震作用下桥上无缝道岔的纵向动力响应，深入认识地震荷载经桥梁结构向无缝道岔传递的过程，分析无缝道岔在地震作用下的敏感参数和薄弱环节。

近年来，国内学者分别采用不同的分析方法，针对不同的桥梁，分析了桥上无缝线路的地震响应规律。其中，黄艳[10-11]自编程序分析了桥上无缝线路钢轨约束、桥墩纵向刚度、线路纵向阻力大小以及桥梁跨数等因素对桥梁抗震的影响；闫斌[12-13]考虑非一致激励、桥墩塑性铰以及梁体碰撞等因素建立了地震作用下的梁轨相互作用模型，主要分析高速铁路的中小跨度简支梁桥、连续梁桥及单塔斜拉桥在一致激励和行波效应下的地震反应规律；刘文硕[14]研究了考虑轨道约束的大跨度钢桁拱桥地震响应，分析了地震波频谱特性、多点激励(场地相位差)等作用下大跨度钢桁拱桥梁轨的响应特性，总结了道床阻力、滑动支座摩擦效应、相邻结构支座布置、墩台刚度以及多荷载耦合等因素对于钢桁拱桥梁轨系统地震响应的影响规律；魏贤奎[15]研究了二期恒载、地震波频谱特性、结构阻尼比、竖向地震作用、铺设小阻力扣件、拱肋温差和拱桥桥跨布置方式等因素对上承式拱桥上无缝线路地震响应规律的影响，并设计了实验室内有砟轨道桥上无缝线路纵向地震反应振动模型试验，依据试验结果对模型中线路阻力参数进行修正和优化；谢铠泽[16]建立了考虑地震作用下桥梁与轨道结构相互作用的REJ-桥-墩一体化计算模型，分析了地震波频谱特性、行波效应、活动支座摩擦系数、REJ布置方式与位置以及地震波加速度峰值等对REJ伸缩量的影响。

图2 地震作用下有砟轨道桥上无缝道岔模型

地震作用下桥上无缝线路的研究近年来虽有所发展，但仍不深入，对桥上轨道结构的受力变形、钢轨强度和线路稳定性等问题研究较少，而且地震作用下的桥上无缝道岔响应研究仍为空白，亟待对其在地震荷载激励下的响应规律和影响因素予以研究和阐述。以一座铁路常见连续梁桥为例，建立地震作用下岔-桥-墩动力非线性有限元模型，对比无钢轨约束、无缝道岔约束工况下桥梁自振频率的变化，分析地震波频谱特性、地震动加速度峰值、岔区阻力、梁体温差因素对桥上无缝道岔地震响应的影响，在此基础上对地震多发地区的桥上无缝道岔设计检算提出相应建议，为震区铁路桥上无缝道岔的设计与维护提供理论指导。

1 桥上无缝道岔纵向地震响应计算模型

1.1 计算模型

当桥梁结构受到地震荷载动作用时，桥墩首先产生受迫震动，墩顶产生位移并通过支座约束传递给整个梁体。假定梁体的固定端在左端，活动端在右端，在某时刻梁体相对于钢轨活动端运动，同时通过道床、扣件带动钢轨向活动端移动，钢轨位移受到路基上道床纵向阻力的约束，使得固定端以外的线路阻力拉着钢轨使其受拉，活动端以外的线路阻力顶住钢轨使其受压，同时道岔间的直曲基本轨与直曲尖轨之间、长短心轨与翼轨之间由于限位器、间隔铁的约束作用产生轨条附加力。钢轨受到附加纵向力后，各截面将产生相应的位移。这些附加力又反作用于梁跨或固定支座，墩顶发生纵向位移，使墩台产生弹塑性变形，最终达到岔-桥-墩相互平衡的状态，如图1所示。

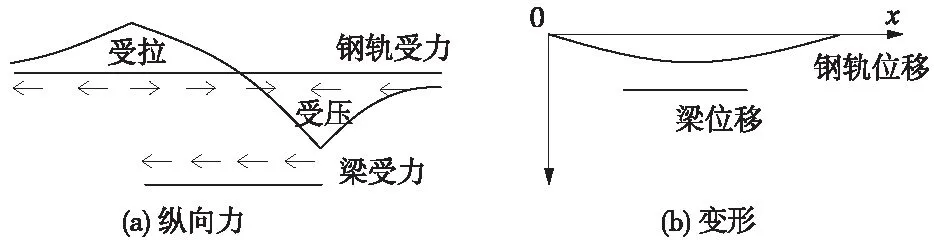
图1 地震作用下桥上无缝道岔梁轨相互作用示意

根据地震作用下桥上无缝道岔梁轨相互作用原理，建立了如图2所示地震作用下岔-桥-墩动力非线性有限元模型。以典型的单线铁路连续梁桥为例进行计算，桥址位于Ⅰ类场地处，桥跨布置：3×32 m预应力混凝土简支箱梁+(32+48+32) m预应力混凝土连续箱梁+3×32 m预应力混凝土简支箱梁。

线路纵向阻力包括扣件纵向阻力和道床纵向阻力，取值参照《铁路无缝线路设计规范》[17]、《无缝道岔计算理论与设计方法》[5]，考虑到两者在循环往复荷载作用下变化特性的不同，根据实际情况分开建模，均考虑为理想弹塑性的恢复力模型。钢轨、梁体采用梁单元模拟，通过设置梁体质量单元来模拟二期恒载；下部墩台和桩基采用梁单元及弹簧单元模拟，考虑桥墩底部塑性铰效应；桥梁固定支座按线性弹簧处理，刚度取为1.0×108N/m，活动支座按理想弹塑性弹簧模拟，摩擦系数为0.03[18-19]，开始滑动的临界位移可取为3 mm，滑移前支座刚度为40 kN/m，支座恢复力模型采用与线路阻力恢复力模型相同的理想弹塑性滞回模型。以一定长度路基计算段为边界条件，为尽可能减少计算长度不同产生的差异，路基计算长度取120 m。

1.2 振动方程建立

根据上述计算模型，地震作用下任意时刻结构动力平衡方程如下

(1)

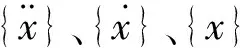
[C]=α[M]+β[K]

(2)

式中，α、β分别为质量阻尼系数和刚度阻尼系数，这两个阻尼系数可通过振型阻尼比计算得到，即

(3)

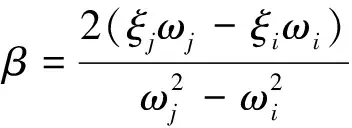
(4)

其中，ωi、ωj分别为结构的第i阶和j阶固有频率；ξi、ξj为相应于第i阶和j阶振型的阻尼比，这里取0.05。

1.3 模型验证

为验证地震作用下桥上无缝道岔模型建立方法及求解程序的正确性，以文献[11]中的3跨32 m简支梁为例，均采用理想弹塑性模型模拟线路阻力，线路纵向阻力取为10 kN/m，极限位移取2 mm，输入8度EI Centro地震波，如图3所示，进行地震作用下钢轨纵向力分布规律和峰值的对比，提取左右桥台处钢轨最大拉压力如表1所示。同时比较了不同线路阻力条件下对钢轨受力的影响(第一跨简支梁右端)，见图4。

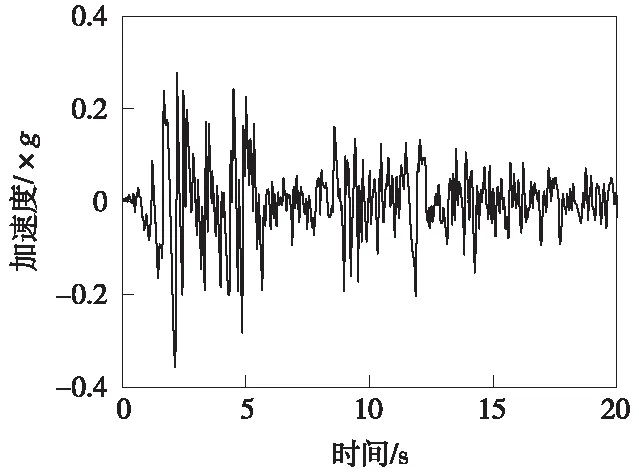
图3 El Centro Site地震波

表1 本文程序计算结果与文献对比 kN

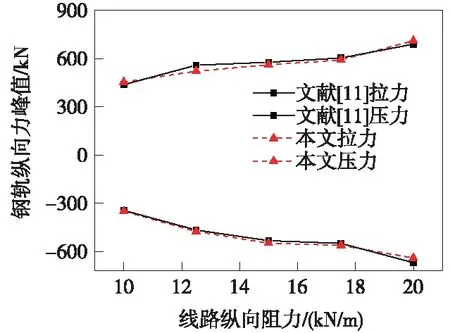
图4 不同线路阻力条件下计算结果对比

由表1和图4可知，本文所建立的模型与文献计算结果在数值和规律上均是一致的，存在少许差异，这是因为桥上无缝道岔模型不同于桥上无缝线路模型而引起的差异，但整体相对误差较小(差异在10%以内)，验证了本文建立的地震作用下桥上无缝道岔动力非线性模型的正确性，可以用来分析地震作用下桥上无缝道岔的受力与变形响应规律。

2 桥上无缝道岔纵向地震响应

2.1 道岔约束对桥梁自振频率影响

根据上节中建立的有砟轨道连续梁桥上无缝道岔有限元模型，分析无钢轨约束、无缝线路钢轨约束和无缝道岔钢轨约束3种条件下，连续梁桥前10阶自振频率和振型特点，如表2所示。

由表2可知，考虑无缝线路和无缝道岔约束作用下，不仅提高了桥梁结构的自振频率而且改变了其振动形态。轨条约束提高了桥梁的低阶振动频率，这是因为桥上铺设无缝线路或无缝道岔时，轨条数增多，道床阻力增强，线路阻力的约束作用限制了梁体和桥墩的变形。同时铺设无缝线路或无缝道岔还改变了桥梁结构的振动形态，第4阶、第8阶振动形态从整体纵飘变为整体横弯，第5阶、第10阶振动形态从整体横弯变为整体纵飘。

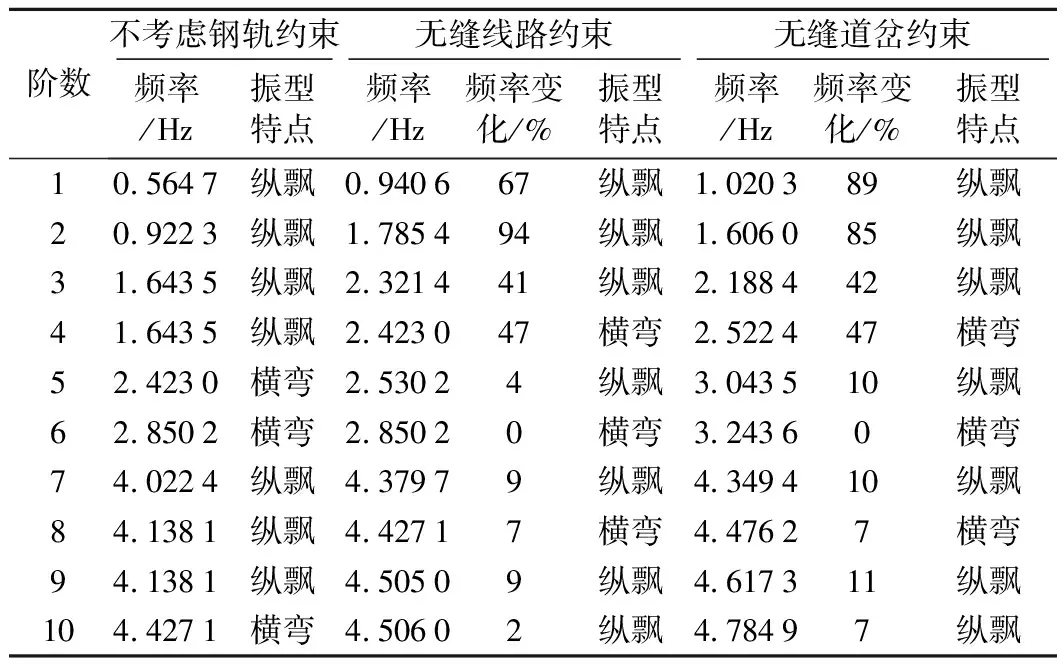
表2 桥梁前10阶自振频率及振型信息

2.2 钢轨纵向力响应

为了比较不同频谱特性地震波的影响，同时选取EI Centro波、San Fernando波、James RD波(分别记为S1波、S2波、S3波)，如图5所示。S1波、S2波、S3波作用下钢轨纵向力峰值包络线如图6所示。

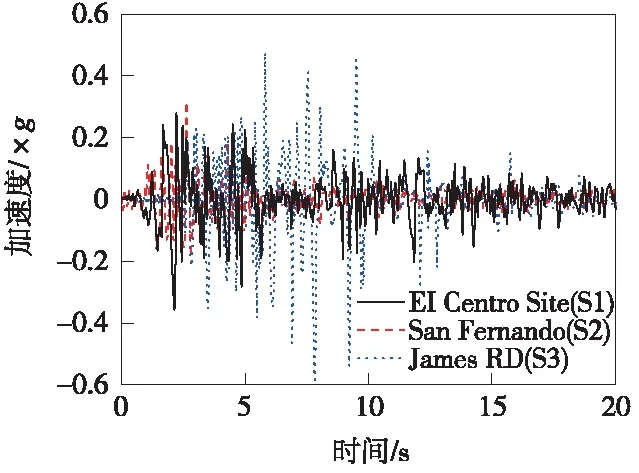
图5 地震波加速度时程

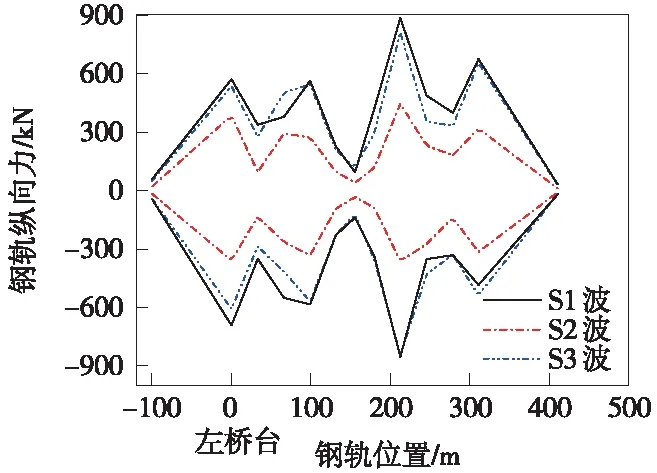
图6 钢轨纵向力包络值

从图6可以看出，地震作用下桥上无缝道岔的钢轨纵向力最大值发生在6号梁缝处，在梁轨相对位移较小的连续梁跨中位置纵向力相比梁缝处要小很多，这与梁体温差荷载下作用规律相似。在加速度峰值(0.1g)相同的条件下，S1波、S3波作用下的直基本轨最大纵向力比S2波计算结果较大，这是因为S1波、S3主频分别为1.40、1.47 Hz，地震波能量集中在0.58～2.0 Hz内，最接近连续梁桥一阶主频1.02 Hz，容易使得连续梁桥在短时间内出现共振，导致结构受力变形急剧增大。

2.3 梁轨相对位移响应

在位移响应方面，S1地震波作用下各关键点处梁轨相对位移时程曲线如图7所示，3种不同频谱特性地震波作用下6号墩位置的梁轨相对位移时程如图8所示。

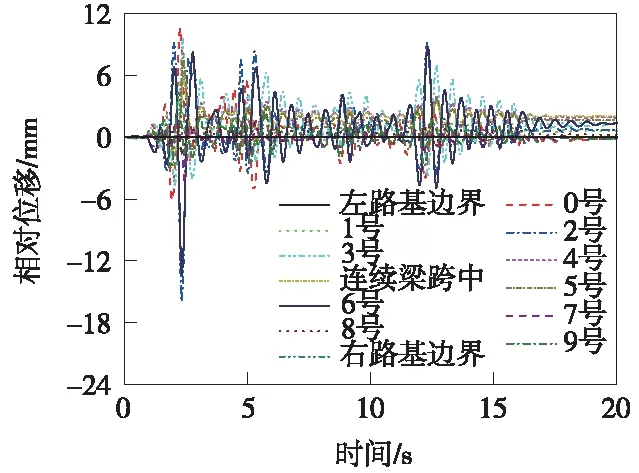
图7 S1波作用下梁轨相对位移时程

图8 6号墩处梁轨相对位移时程

由图8可知，在不同频谱特性的地震波对应的梁轨相对位移最大值不同，S1波、S3波作用下的梁轨相对位移比S2波作用结果要大，该规律与上节中钢轨最大纵向力分析原因相同，不再赘述。其中S1、S2、S3波作用下梁轨残余相对位移分别为1.4、0.2、0.9 mm，道岔钢轨、梁体位移均未停留在平衡点位置是因为线路阻力的非线性和桥墩塑性铰的非线性造成的。

3种地震波作用过程中的梁轨相对位移均超过4 mm，地震荷载与列车制启动荷载类似，在较短时间内发生，短时间内过大的梁轨相对位移会改变道床阻力状态，破坏道床结构、降低道床纵横向阻力，增加道床离散性，影响线路稳定性。

2.4 道岔关键部件受力与变形响应

3种不同频谱特性地震波作用下桥上无缝道岔联结件限位器、间隔铁受力、直曲尖轨相对基本轨位移、长短心轨相对翼轨位移、转辙机处基本轨相对桥梁位移最大值计算结果见表3。

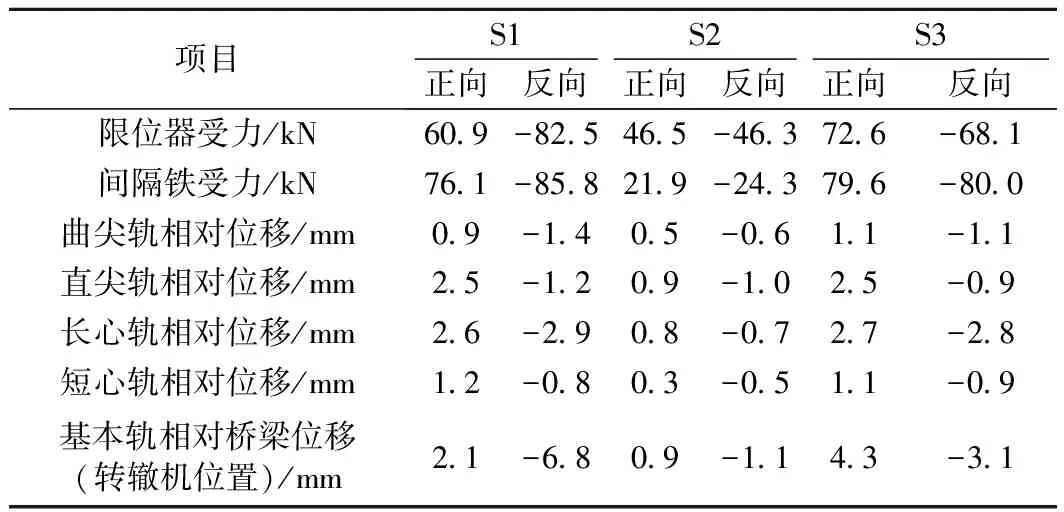
表3 不同地震波下的道岔联结件受力以及关键点相对位移

为保证无缝道岔的安全运营，需进行限位器以及间隔铁联结螺栓强度检算以及尖轨心轨相对位移检算。其中S1波作用下的限位器和间隔铁受力最大，最大限位器纵向力为-82.5 kN，间隔铁最大纵向力为-85.8 kN，均能满足规范要求。

表3列出了道岔自由伸缩部分关键位置的相对位移，比较3种不同地震波激励，直曲尖轨相对基本轨位移、长短心轨相对翼轨位移较小均能满足规范要求。3种地震波作用下对应的转辙器、辙岔两部分转辙机处基本轨相对桥梁正、反位移的最大值为4.3、-6.8 mm，已超过规范限值，应提高转辙机动作杆、连接杆的材料强度，同时震后应及时检查连接杆、锁闭杆是否发生弯折扭转，以及道岔线型是否满足要求，确保道岔转换系统正常以及行车安全。

3 桥上无缝道岔纵向地震响应影响因素分析

3.1 地震加速度峰值影响

为探讨不同加速度峰值地震作用下桥上无缝道岔的响应规律，选取S1(El Centro)地震波，将峰值调整为0.05g、0.1g、0.3g，分别相当于抗震设防烈度为6、7、8度设计地震。钢轨纵向力与梁轨相对位移的峰值、道岔关键部件的受力与变形计算结果汇总见表4、表5。

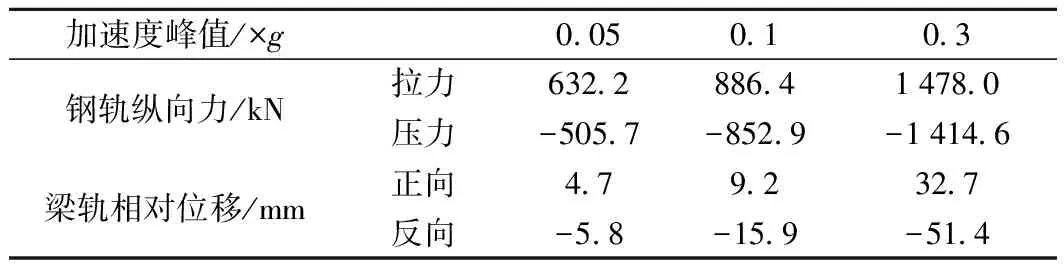
表4 不同地震加速度峰值时钢轨最大受力与变形

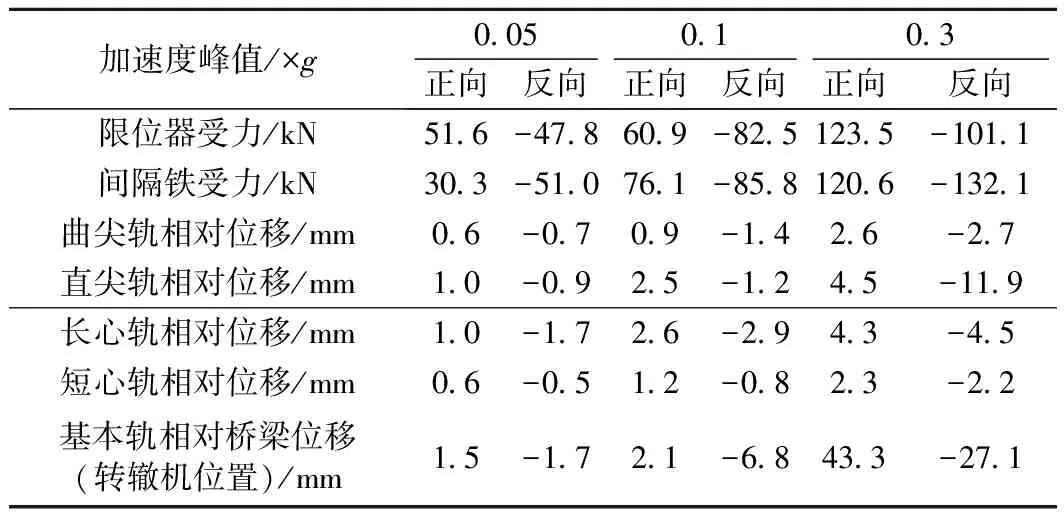
表5 不同地震加速度峰值时道岔联结件受力

从表4可以看出，加速度峰值对地震波作用下结构响应影响显著，随着加速度峰值的增大，钢轨纵向力、梁轨相对位移随之相应增长。高烈度地震荷载作用下梁轨相对位移要远大于列车荷载制、启动作用下的梁轨相对位移，在连续梁右端的梁缝位置，仅a=0.3g的8度区设计地震烈度时梁轨相对位移最大值就为51.4 mm，已远超过4 mm。

从表5可知，限位器和间隔铁受力均随着加速度峰值的增大而增加，峰值未超过容许限值373 kN。但在转辙机处梁轨相对位移方面，当加速度峰值a=0.3g时其最大值达到了43.3 mm，是高烈度地震作用下过大的梁轨相对位移较大导致的。高烈度地震作用下，桥上无缝道岔基本轨相对桥梁位移得不到保障，转辙机动作杆、连接杆、锁闭杆之间容易出现较大的错动，杆件被折断，转辙机无法实现转换功能，影响行车安全。

3.2 岔区阻力影响

考虑到岔区纵向阻力形式的多样性，道床结构的离散性，以及有砟、无砟轨道岔区阻力的不同，因此有必要分析在不同大小的岔区阻力下地震作用桥上无缝道岔响应分析。不考虑扣件纵向阻力变化，在基本工况的基础上，分别计算岔区道床纵向阻力系数α=1.0、2.0、4.0三种工况下的桥上无缝道岔的地震响应规律。计算结果见表6、表7。

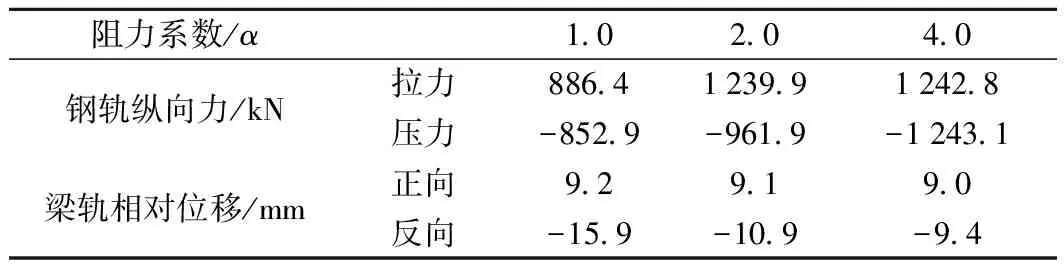
表6 不同岔区阻力时钢轨、桥墩最大受力与变形

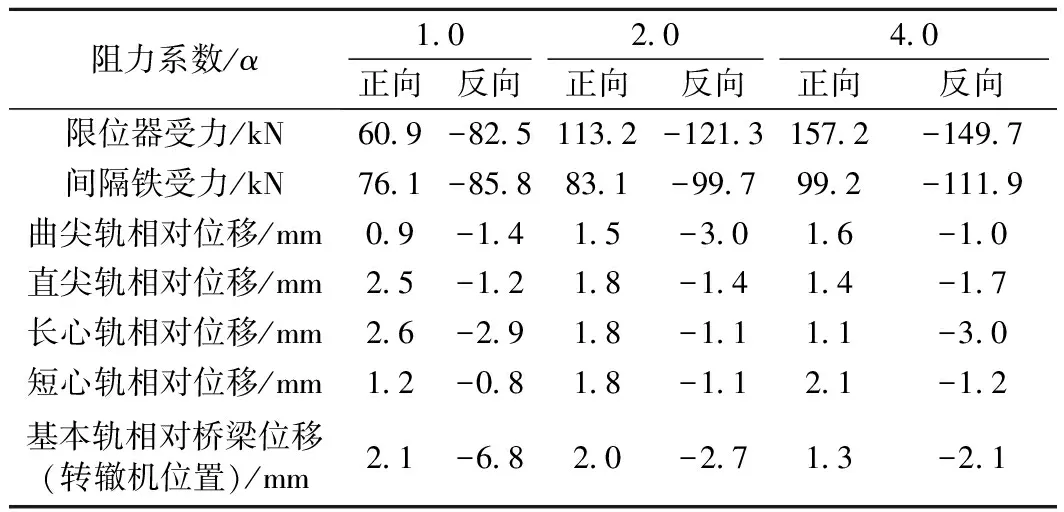
表7 不同岔区时道岔联结件受力以及关键点相对位移

从表6可以看出，随着道床纵向阻力的增大，梁轨相互约束作用增强，地震作用下上部轨道结构会耗散掉更多的能量，轨条纵向力增加，梁轨相对位移减小，并呈非线性关系。从表7可得，随着纵向阻力的增加，道岔限位器、间隔铁受力增加，但均未超过限值373 kN。曲尖轨、长心轨、短心轨的相对位移均随着阻力系数的增大变化不大，相比于规范限值仍然较小，均满足小于5 mm要求。

3.3 梁体温差影响

工程实际中，由于地震的突发性，很有可能发生在一天之内当地气温最高或最低点，此时必然会伴随着环境温度的作用。梁体温差的存在使得钢轨内部本身已经聚集了较大的温度附加力，再加之地震纵向作用的耦合，钢轨内力在两因素同时作用下重新分布，极有可能造成轨缝增大，轨条被拉断。首先以仅梁体降温15 ℃为例，3号、4号、连续梁跨中、5号、6号位置的钢轨纵向力时程如图9所示，不同降温条件下连续梁右端6号梁缝位置的钢轨纵向力时程如图10所示。

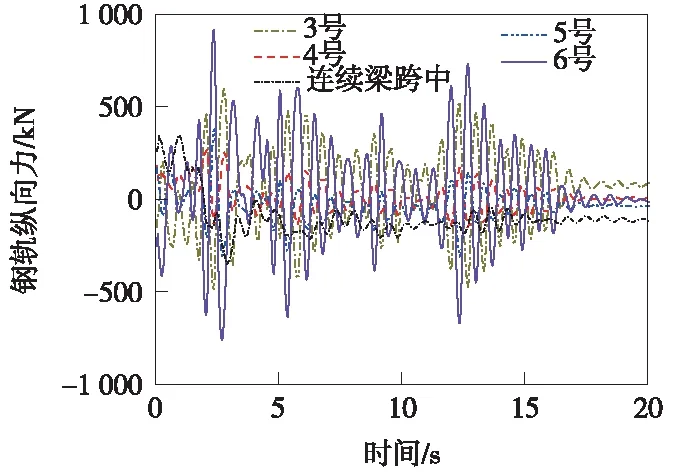
图9 梁体降温15 ℃钢轨纵向力时程

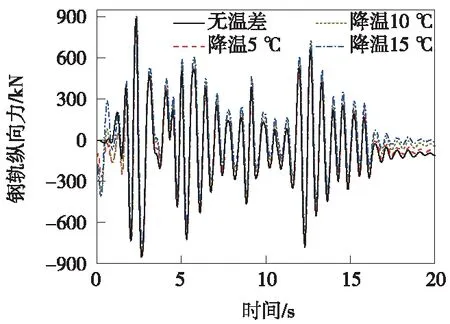
图10 6号梁缝位置钢轨纵向力时程

从图9、图10可以看出，由于在地震力发生之初，在梁体降温条件下梁轨系统中已经存在着初始附加力和初始位移，钢轨最大纵向附加力发生在连续梁右端梁缝位置，降温5、10、15 ℃对应的钢轨附加力最大值分别为116.1、217.1、254.3 kN。随后桥梁受到地震外部激励，造成梁体纵向平动，与初期温度荷载下的桥梁位移叠加，使得桥上无缝道岔钢轨纵向力重新分布。从图10可以看出，在不同梁体温降条件下，仅初始1 s内的钢轨纵向力时程不同，随后钢轨纵向力变化有地震作用控制，不同初始温变对应的钢轨纵向力相差不大。

进一步分析钢轨、梁体共同温变条件下桥上无缝道岔地震响应规律，见图11及表8。同时比较了地震作用前后轨条附加力变化情况，见图12。

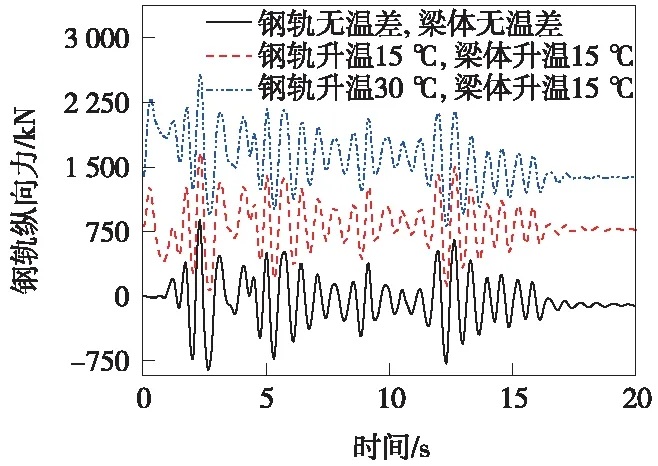
图11 6号梁缝位置钢轨纵向力时程

表8 升温条件下道岔受力与变形

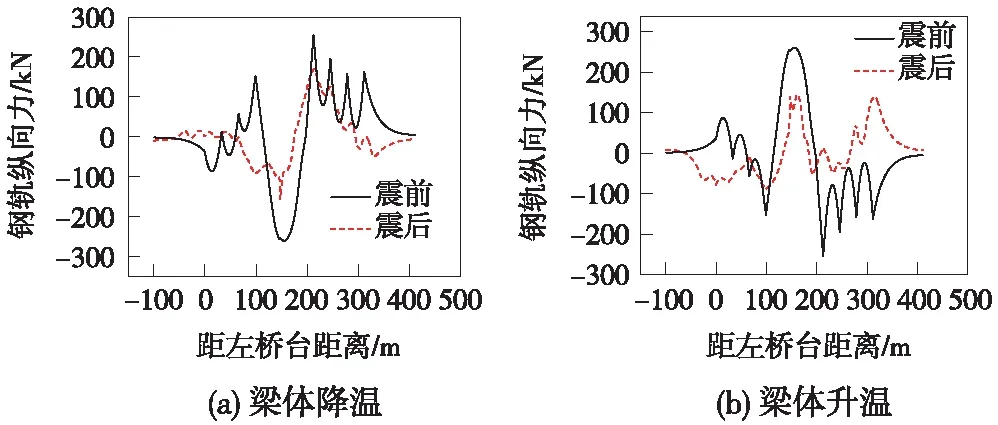
图12 钢轨纵向附加力震前震后比较

从图11钢轨纵向力时程规律可以得出，同时考虑梁轨温变时，钢轨纵向力变化趋势不变，相当于在原有钢轨附加力基础上增加了钢轨温度力。而且从图中可以看出，钢轨纵向力最大值已达到2555.4 kN，钢轨最大应力为329.9 MPa，在未考虑动弯应力、制动附加力的情况下，已接近U71MnG钢轨允许应力352 MPa。可以得出，在钢轨温变较高，又同时考虑地震荷载效应时，钢轨强度和线路稳定性均得不到保障。

从表8可以看出，在同时考虑钢轨、桥梁温变时，地震作用下的桥上无缝道岔联结件受力、关键点位置变化聚增。当钢轨温升30 ℃，梁体温升15 ℃时，道岔间隔铁最大受力为411.5 kN，超过容许纵向力限值373 kN。直曲尖轨、转辙机处梁轨相对位移也都超限。

从图12可以看出，震后钢轨纵向力分布规律和峰值均发生了较大变化，梁缝和跨中位置处钢轨纵向力峰值均比震前减小，部分梁缝处甚至出现了钢轨纵向力峰值反向变化，这种现象应与地震作用下线路纵向阻力往复变化对钢轨内力重分布有密切关系。

4 结论和建议

本文建立了地震作用下岔-桥-墩动力非线性有限元模型，分析了地震波频谱特性、地震动加速度峰值、岔区阻力、梁体温差等因素下的有砟轨道桥上无缝道岔地震作用响应规律。主要得到以下几点结论和建议。

(1)因地震波频谱特性对桥上无缝道岔响应影响非常显著，对于铁路桥梁结构抗震设计，可以通过改变桥墩刚度、梁体桥墩质量、支座布置方式以及支座摩擦系数等，使结构低阶自振频率有效地避开场地处地震波的低阶频段。

(2)桥上无缝道岔设计阶段，在桥梁抗震设防等级为7级设计地震烈度及以下时，对有砟轨道桥上无缝道岔的设计检算，将《铁路无缝线路设计规范》(TB10015—2012)中的伸缩工况、挠曲工况、制动工况重新考虑为钢轨温变、梁体温变与地震荷载组合工况、挠曲与地震荷载组合工况与地震荷载组合工况(取两者中的较大值)、制动工况，见表9；道岔联结件、关键位置相对位移也按梁体温变与地震荷载组合工况下计算结果取值，与规范限值比较。

表9 设计地震下轨道强度及稳定性检算组合

注：轨道稳定性容许力1 950 kN为新Ⅲ型桥枕60 kg/m钢轨无缝线路理论值[17]。

(3)桥上无缝道岔设计阶段，当桥梁抗震设防等级为7级设计地震烈度以上时，建议轨道结构设计仍按7级设计地震荷载考虑。当高烈度或罕遇地震发生时，路基、桥梁、隧道结构均极易发生破坏，即使按极高标准设计，也很难达到要求，同时得不到保证，此时已无研究铁路轨道结构抗震意义。

(4)在线路养护维修方面，震后应及时对桥上无缝道岔状态进行评估，包括钢轨应力是否超限，道床纵横向阻力大小，对线路发生屈曲失稳，线性破坏的线路，应及时整治矫正。检查限位器、间隔铁联结螺栓是否被剪坏，尖轨心轨相对位移是否超限，转辙机处动作杆、连接杆、锁闭杆是否发生弯折扭转，确保道岔转换系统工作正常及行车安全。

[1] 叶爱君.桥梁抗震[M].北京：人民交通出版社，2002.

[2] 范立础，卓卫东.桥梁延性抗震设计[M].北京：人民交通出版社，2001.

[3] 范立础，胡世德，叶爱君.大跨度桥梁抗震设计[M].北京：人民交通出版社，2001.

[4] 范立础.桥梁抗震[M].上海：同济大学出版社，2001.

[5] 王平，刘学毅.无缝道岔计算理论与设计方法[M].成都:西南交通大学出版社，2007.

[6] 王平，杨荣山，刘学毅.无缝道岔铺设于长大连续梁桥上时的受力与变形分析[J].交通运输工程与信息学报，2004(3):53-58.

[7] 王平.无缝道岔群对钢轨位移和纵向力的影响研究[J].铁道学报，2002(2):74-78.

[8] 杨荣山.桥上无缝道岔纵向计算理论与试验研究[D].成都:西南交通大学，2008.

[9] 杨荣山，刘学毅，王平.桥上无缝道岔纵向力计算理论与试验研究[J].铁道学报，2010(4):134-140.

[10] 黄艳，阎贵平，刘林.轨道约束对铁路桥梁纵向地震反应特性的影响[J].铁道学报，2002，24(5):124-128.

[11] 黄艳.考虑轨道约束的铁路桥梁抗震研究[D].北京:北方交通大学，2003.

[12] 闫斌，戴公连，徐庆元.行波效应下铁路简支梁桥梁轨系统地震响应[J].振动工程学报，2013，26(3):357-362.

[13] 闫斌.高速铁路中小跨度桥梁与轨道相互作用研究[D].长沙:中南大学，2013.

[14] 刘文硕.高速铁路大跨度钢桁拱桥梁轨相互作用研究[D].长沙:中南大学，2013.

[15] 魏贤奎.铁路拱桥上无缝线路纵向梁轨相互作用与地震反应分析研究[D].成都:西南交通大学，2014.

[16] 谢铠泽，王平，汪力，等.地震动作用对桥上钢轨伸缩调节器的影响分析[J].铁道学报，2016，38(3):111-118.

[17] 中华人民共和国铁道部.TB10015—2012 铁路无缝线路设计规范[S].北京:中国铁道出版社，2013.

[18] 陈学喜，朱晰，高学奎.地震作用下桥梁梁体间的碰撞响应分析[J].中国铁道科学，2005，26(6):75-79.

[19] 杨兆国.强震作用下梁桥的碰撞效应及其响应[D].长沙:湖南大学，2010.

[20] 贺国京，阎奇武，袁锦根.工程结构弹塑性地震反应[M].北京:中国铁道出版社，2005.

[21] 中华人民共和国住房和城乡建设部.GB5011—2006 铁路工程抗震设计规范[S].北京:科学出版社，2012.