基于粒子群算法的树状灌溉管网系统优化设计

王文婷，郭乙霏

(1,焦作市抗旱防汛通讯站，河南 焦作 454150；2.东北农业大学水利与土木工程学院，哈尔滨 150003)

0 引 言

近年来，随着我国经济水平和人口数量的持续增长，我国的水资源供需不平衡、水资源不足等问题显得日益突出，使我国农业现代化进程受到严重的制约。农业作为我国的用水大户，具有巨大的节水潜力，因此节水农业的发展对缓解我国水资源供需不平衡，应对我国水资源不足等有着重要的意义。

在进行农田灌溉时，需要事先从水源地将灌溉水合理、有序、及时的运送到田间。灌溉水的运输作为农业灌溉中不可或缺的环节，对我国节水农业的发展有着重要的意义。自20世纪七八十年代以来，灌溉管网在我国农田灌溉中的应用越来越广泛。利用灌溉管网实现灌溉水的输配在减少蒸发损失和输水损失、提高灌溉水利用效率的同时，也在增大有效灌溉面积、提高土地利用率方面有着明显的成效[1]。此外，灌溉管网系统移动灵活方便，灌溉效率高，容易实现自动化和方便田间管理[2, 3]。因此，在21世纪节水农业发展过程中，管道化灌溉起着举足轻重的作用。

灌溉管网系统的优化设计主要是通过优化数学模型，借助数学方法和计算机技术，寻求模型的最优解，实现对管网系统的优化布置以及管网直径的优化选择，筛选出能使投资达到最小的优化方法[4-6]。近年来，国内外不少学者采用不同的计算方法(如遗传算法、最小生成树算法等)建立起了不同的灌溉管网优化模型，并实现了灌溉管网系统的优化布置。付玉娟[7]、马雪琴[8]、Glodberg[9]等利用基于整数编码遗传算法对灌区树状管网进行优化布置，并通过实例验证，均得到了较优的管网系统布置方案。而后，付亚娟又利用GIS技术对灌溉管网进行优化布置。胡杰华[10]、李密青[11]等则利用最小生成树模型，也实现了灌溉管网系统的多目标优化布置。

粒子群算法(Particle Swarm Optimization，PSO)作为进化算法的一种，从随机解出发，通过适应度来评估所得解的品质，依据追随当前搜索到的最优解来找到全局的最优解，具有收敛快、精度高、易实现等特点[12]。目前，粒子群算法在石油运输管网优化[13-15]和污水管网优化[16]中应用广泛，甚至在配电系统中也有所应用[17-19]。在农田灌溉中，灌溉管网具有与石油、污水等运输管网相似的特点，而PSO算法在农田灌溉管网系统优化布置方面的应用则鲜有报道。

本文在综合分析粒子群算法原理和过程的基础上，将其与树状灌溉管网模型相结合，实现了对灌区灌溉管网系统的优化，最后结合具体实例对我国某灌区灌溉管网系统进行优化并与2级遗传优化模型进行对比，说明了粒子群算法的可行性和优越性。

1 树状灌溉管网数学模型的构建

为了达到灌溉管网造价最低的目标，在进行管网优化时，所使用的数学模型如下：

(1)

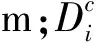
灌溉管网优化模型的约束条件如下。

(1)为了保证管网中各节点压力满足最小压力，需满足以下约束条件：

(2)

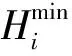
(2)流速约束条件：

Vmin≤Vi≤Vmaxi=1,2,…,n

(3)

式中：Vmin和Vmax分别表示管道允许的最小和最大流速，m/s。

(3)管径约束条件。管道直径需选择标准的可用管径，即：

Di∈[d1,d2,…,dM]

(4)

式中：Di表示管道直径，mm；M表示可供选择的管道直径的个数；d1,d2,…,dM表示可供选择的管道直径，mm。

2 粒子群算法的实现

粒子群算法是基于鸟群捕食行为研究而建立的一种智能简化算法，它最初由kennedy博士和Eberhart博士在1995年联合提出的一种较新的算法[12]。与遗传算法相类似，它也是进化算法的一种[14]。它首先初始化一组随机解，然后借助随机搜索的方法依据适应值来找寻最优值，在离散变量和连续变量的优化中应用较为广泛。

整个PSO算法中，所有粒子都有一个适应度函数(用fit表示，其中fit=1/Z，即为管网总造价的倒数)。在整个研究空间中，所有粒子都有自己的飞行速度和方向，优化过程就是通过个体自身体验(进行局部优化过程)和群体间的信息共享(进行全局优化过程)对粒子的飞行速度和方向进行不断的调整和优化，从而使所有的粒子(整体)都“飞行”到最理想的区域中，因此，基于PSO优化算法的过程即为寻找研究空间中粒子的过程。PSO算法具体流程见图1。

图1 PSO算法基本实现过程

在PSO算法中，假定粒子群落大小为N(即由N个粒子构成)，在m维空间中对目标进行搜索。在优化过程中粒子位置和运动状态信息主要是由Xi=(Xi1,Xi2,…,Xim)、Pibest、Vi(Vi1,Vi2,…,Vim)和gbest决定，它们分别表示粒子当前位置坐标、优化过程中的最优位置坐标(也即个体最优值)、粒子在该时刻的运动速度以及整个粒子群体在优化过程中的最优位置坐标(也即全局最优值)。各个粒子都是通过以下2个方程来调整其速度和方向的。

(5)

(6)

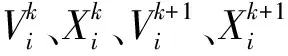
3 工程实例应用

3.1 已知条件

以我国某灌区为例，对该灌区的管网布置系统进行优化处理。考虑实际情况，在使用灌区树状灌溉管网进行供水时，各个结点必须满足有且只有一个供水管道为其供水，这就需要从多个可能供水管道进行优化选择，从而确定出所有结点的供水管道，组成最终的优化供水管网。该灌区中所有可能的灌溉管网布置见图2，共10个供水节点(其中0点为水源点)，26种可能的供水连接方案。每个节点的进水管道按照逆时针方向用整数代码进行命名，如图2中的节点2，按照逆时针方向将3个供水管道依次编码为0，1，2。该灌溉管网中可用的管道直径和管道价格见表1，并按照管径从小到大的顺序依次编码。在该管网系统中，允许最大和最小流速分别为3.0和0.5 m/s，压力水头为10 m。表2给出了各个管段编号及管段长度等。

图2 某灌区灌溉管网初步布置

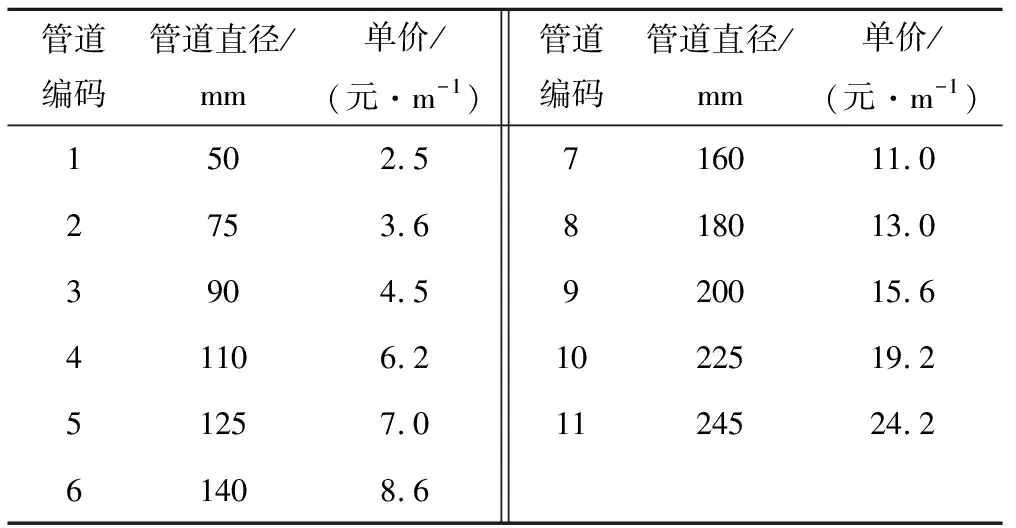
表1 可选用的管道规格

各个管段编号按照“流出结点-供水管道编码-流入结点”的方式进行命名，例如：a-0-b。表3给出了0～9各供水结点高程和需水量等数据。

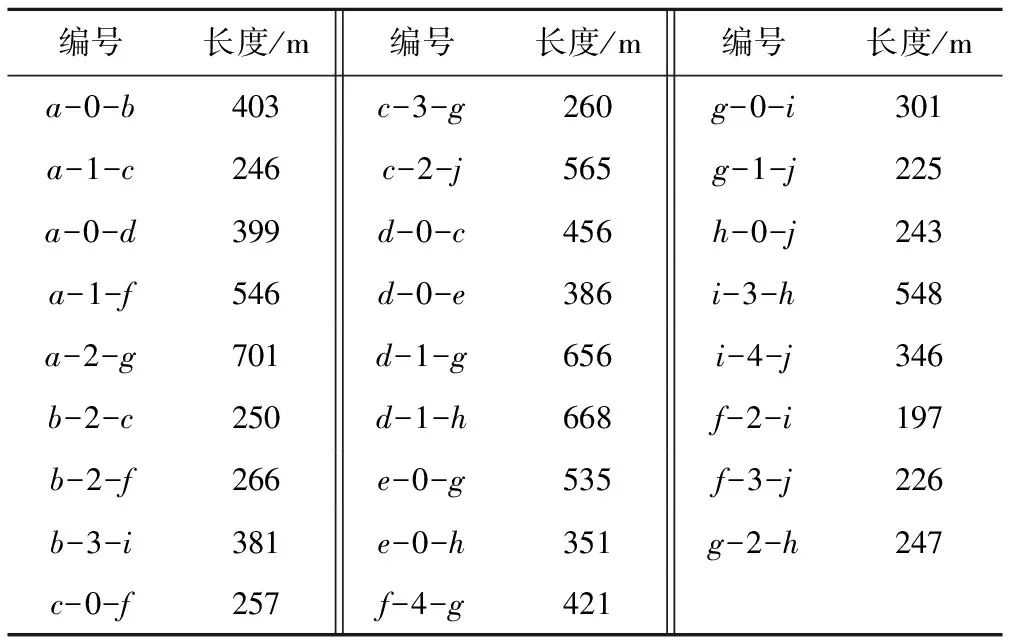
表2 灌溉管网中各管段长度 m

表3 灌溉管网中各个供水结点数据

3.2 模型计算结果

利用matlab 14a软件进行对粒子群算法进行编程计算，本文中各系数取值如下：c1=0.5，c2=2.0，w=0.95，N=200，最大迭代次数为100，通过计算可得到造价最低且符合实际的最优方案。 PSO优化过程中适应度值变化情况见图3。文中通过PSO优化得到的管网总长度为2 620 m，总投资金额为1.193 万元。文献[4]中通过2级优化遗传模型优化得到的投资总金额和管网总长度见表4。通过比较可知PSO优化算法可减少3.7%的管网用量，减少27.8%的投资金额，同时在PSO算法中还给出了最优的管道组合，管道流速等信息，见表4。

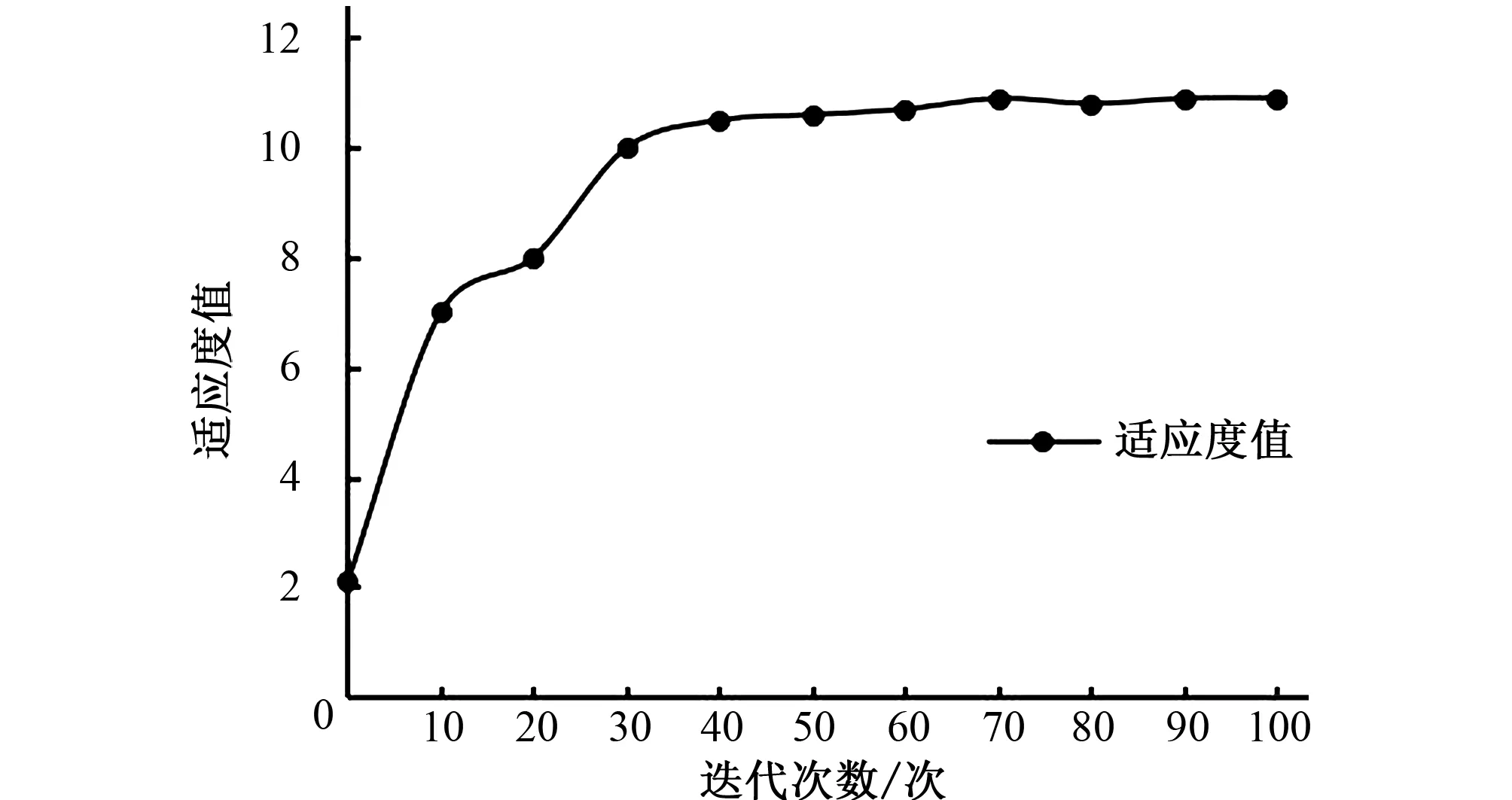
图3 PSO算法优化过程适应度值变化情况

图4和图5分别给出了基于2级遗传优化模型和基于PSO算法得到的灌区优化管网布置形式。在2级遗传优化模型得到的管网优化布置形式中只有一个总投资额和总管长的优化值，并没有说明管道流速和管道长度。所以在文献[4]中的总投资额应是一个估计值，而实际值应较估计值略低。通过与原设计方案比较可知，使用PSO算法得到的灌溉管网优化结果中总投资额度更少，灌溉管网总长度也更短，有利于节约投资成本，且符合实际情况。

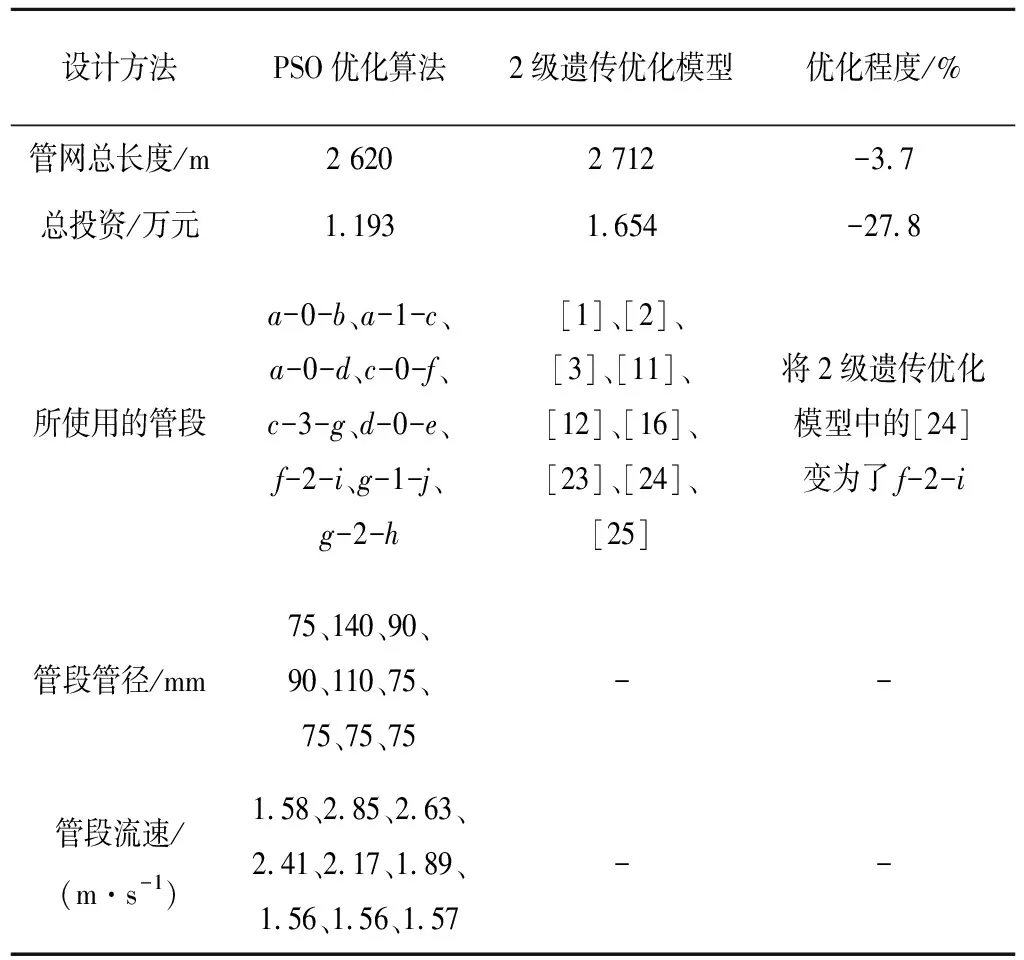
表4 灌溉管网优化布置对比

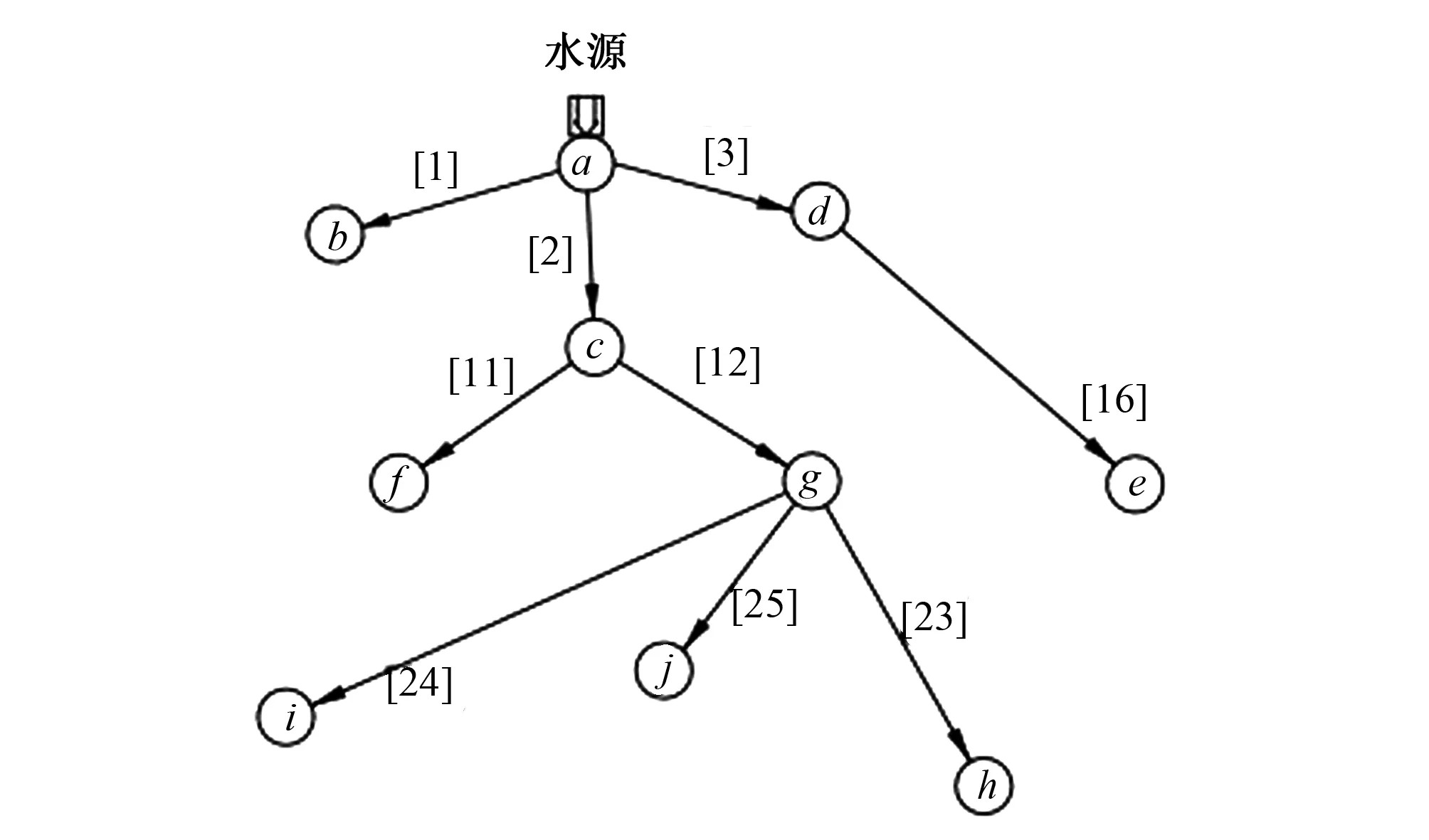
图4 基于2级遗传优化模型优化的灌区最优管网布置

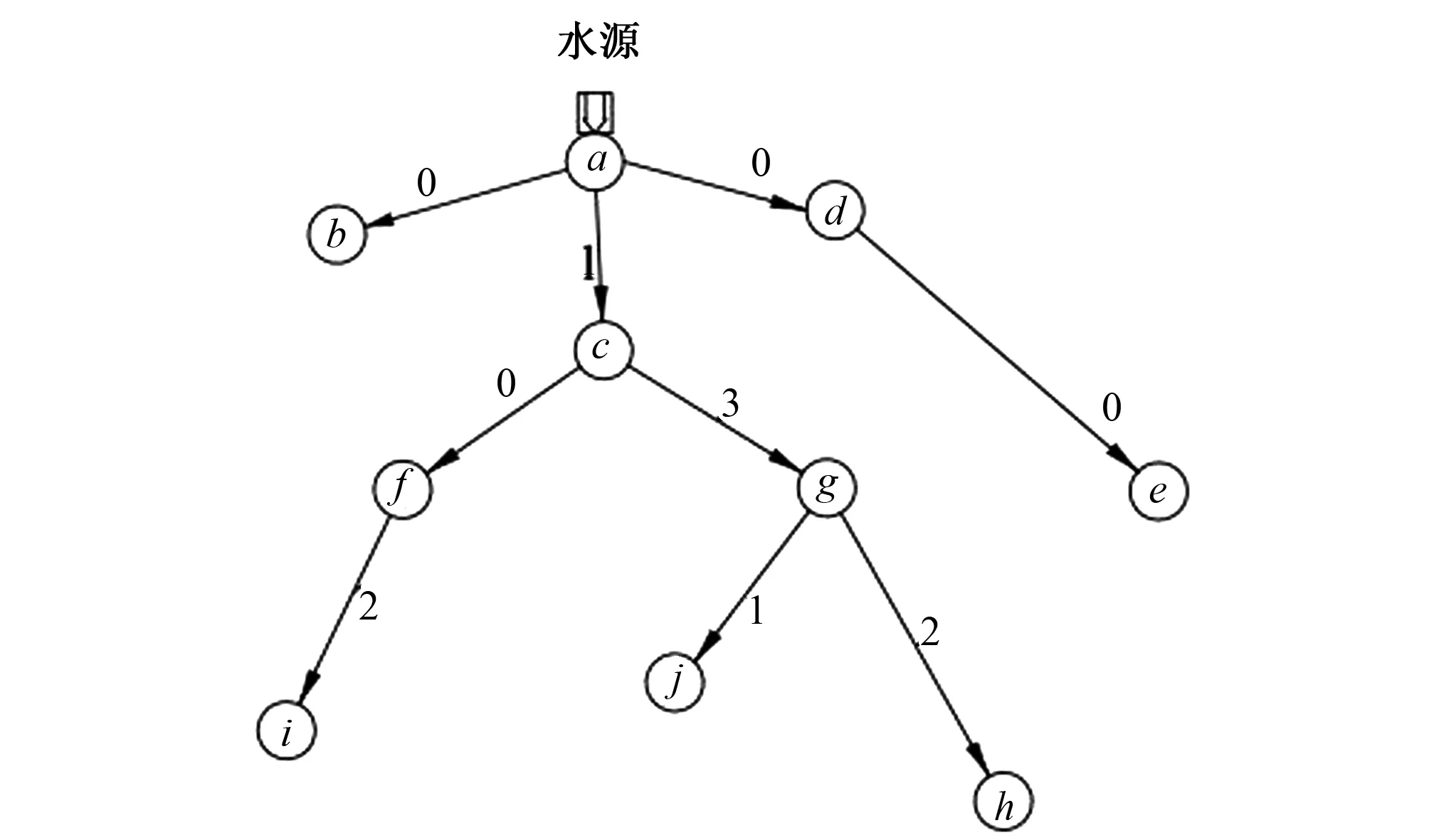
图5 PSO算法优化的灌区最优管网布置

4 结 语

本文基于树状灌溉管网中单点供水的原则，将PSO优化算法与农田水利工程中的灌溉管网优化模型相结合，提出了基于PSO优化算法的树状灌溉管网优化模型。而后针对具体的实例对我国某灌区树状灌溉管网系统进行优化，得到了最终的优化方案。与2级遗传优化模型得到的方案相比，使用该优化算法得到的最优管网布置的复杂度最小，需要的管网长度最小，投资成本最低，同时也能够满足灌区实际灌溉需求。本研究为PSO算法在灌溉管网优化布置中的应用提供了参考依据。

：

[1] 付玉娟,蔡焕杰. 灌溉管网优化研究现状与展望[J].西北农林科技大学学报(自然科学版),2005,33(11):137-140.

[2] 付玉娟. 基于GIS的灌溉输配水管网优化研究[D]. 陕西杨凌:西北农林科技大学,2008.

[3] 马朋辉. 灌区微灌独立管网系统优化设计研究[D]. 陕西杨凌：西北农林科技大学,2016.

[4] 王 昕,马海燕,张 禾.等 规模化管道输水灌溉管网优化模型研究与应用[J].节水灌溉,2015,(10):87-89.

[5] 胡良明,李 仟,郑佩佩. 基于遗传算法的农村供水管网优化设计[J].人民黄河,2017,39(1):102-105.

[6] 周荣敏,雷延峰. 管网最优化理论与技术[M].郑州:黄河水利出版社,2002.

[7] 付玉娟,蔡焕杰,张旭东. 基于遗传算法的树状灌溉管网优化设计[J].人民黄河,2006,28(7):42-44.

[8] 马雪琴,吕宏兴,朱德兰. 基于遗传算法的树状灌溉管网优化设计[J].中国农村水利水电,2013,(4):50-52.

[9] Goldberg D E,Kuo C H. Genetic algorithms in pipeline optimization[J].Journal of Computing in Civil Engineering,1985,1(2):128-141.

[10] 胡杰华,马孝义,姚慰炜. 基于最小生成树模型的树状灌溉管网的优化设计[J].中国农村水利水电,2012,(2):1-3.

[11] 李密青,郑金华,罗 彪. 一种基于最小生成树的多目标进化算法[J].计算机研究与发展,2009,46(5):803-813.

[12] 刘建华. 粒子群算法的基本理论及其改进研究[D].长沙：中南大学,2009.

[13] 蔡昌新. 粒子群算法在油田管网优化中的应用[J].长江大学学报(自然科学版：理工卷),2010,7(3):80-82,737.

[14] 柯文奇. 基于粒子群算法原油集输管网优化[J].石油规划设计,2010,21(1):15-17,50.

[15] 黄 晶. 基于粒子群算法的油田注水管网优化研究[D]. 黑龙江大庆市：大庆石油学院,2009.

[16] 薛英文,文倩倩. 基于粒子群算法的污水管网优化设计[J].中国农村水利水电,2010,(8):40-42.

[17] 俞隽亚,王增平,孙 洁. 基于支路交换----粒子群算法的配电网故障恢复[J].电力系统保护与控制,2014,42(13): 95-99.

[18] 张君则,艾 欣. 基于粒子群算法的多类型分布式电源并网位置与运行出力综合优化算法[J].电网技术,2014,38(12):3 372-3 377.

[19] Mehdinejad M,Mohammadi-Ivatloo B,Dadashzadeh-Bonab R. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms[J].International Journal of Electrical Power & Energy Systems,2016,83:104-116.