基于多岛遗传算法的漂浮式风力机TMD参数优化

周红杰， 丁勤卫， 李 春,2， 郝文星， 余 万

(1.上海理工大学 能源与动力工程学院，上海 200093;2.上海市动力工程多相流动与传热重点实验室，上海 200093)

随着陆上风电场可开发资源的减少，未来风电场建设的必然趋势是“由陆向海、由浅到深、由固定基础向漂浮式平台”[1-2]。海上风能作为一种正在蓬勃兴起的新能源，相对于陆上风能具有湍流强度小、靠近负荷中心、视觉及噪声污染小等优点[3-5]。相比浅水区固定式基础风力机，漂浮式风力机因受到风、浪、流等多种环境载荷综合作用，漂浮式平台的摇荡运动不仅会影响机舱内传动系统的正常工作，降低风力机的发电效率，甚至可能导致塔架的屈曲和倾覆等事故，将造成不可估量的损失[6-8]。因此，对于海上风力机而言，如何保证整机稳定安全运行是一个亟待解决的问题。

目前，国内外一些学者为解决漂浮式风力机的稳定性问题进行了相关研究。Namik等[9]提出了应用于海上漂浮式风力机的叶片独立变桨技术，计算了漂浮式风力机在环境载荷大小方向均一致的情况下，叶片独立变桨技术与统一变桨技术对平台运动的控制效果。Fischer等[10]提出一种基于加速度反馈的非线性控制方法，在理论上分析了漂浮式风力机的稳定性。Dunne等[11]提出一种新型的基于激光雷达的前馈控制策略，通过预测来流风速，提前控制桨距变化以达到减小负载的目的；贾文强等[12]将变速变桨策略运用到海上风力机的控制，对相同控制策略下的陆、海风力机进行了仿真。上述几种控制策略均侧重于通过控制叶片上的气动载荷来提高漂浮式风力机整体的稳定性，较少采用基于结构控制的方法，并且虽然几种控制策略均有一定的控制效果，但仍存在叶根疲劳载荷过大的缺点。因此，对采用结构控制方法来实现海上风力机稳定运行的研究十分必要。

借鉴传统高耸结构的稳定性控制方法，Lackner等[13]提出将调谐质量阻尼器(Tuned Mass Dampers，TMD)应用于漂浮式风力机的思路，并对控制效果进行了初步研究，但其并未进行TMD的参数优化分析，因而导致TMD对塔架顶端振动位移及平台横摇响应的抑制效果并不明显。因此，笔者采用多岛遗传算法对Barge型漂浮式风力机配置TMD的参数进行全局优化，以期为海上漂浮式风力机的稳定性控制提供一定的理论参考。

1 漂浮式风力机及TMD模型

选取基于ITI Barge型NREL 5 MW漂浮式风力机为研究对象，该风力机参数详见文献[14]，ITI Barge平台主要参数详见文献[15]。在环境载荷作用下，漂浮式风力机可视为6自由度的刚体，6自由度上的运动包括沿x轴、y轴和z轴的平动及绕各轴的转动。平动包括纵荡(Surge)、横荡(Sway)和垂荡(Heave)，其大小由长度单位表示；转动包括横摇(Roll)、纵摇(Pitch)和首摇(Yaw)，其强弱由角度单位表示。漂浮式风力机Barge平台在6自由度上的运动如图1所示。

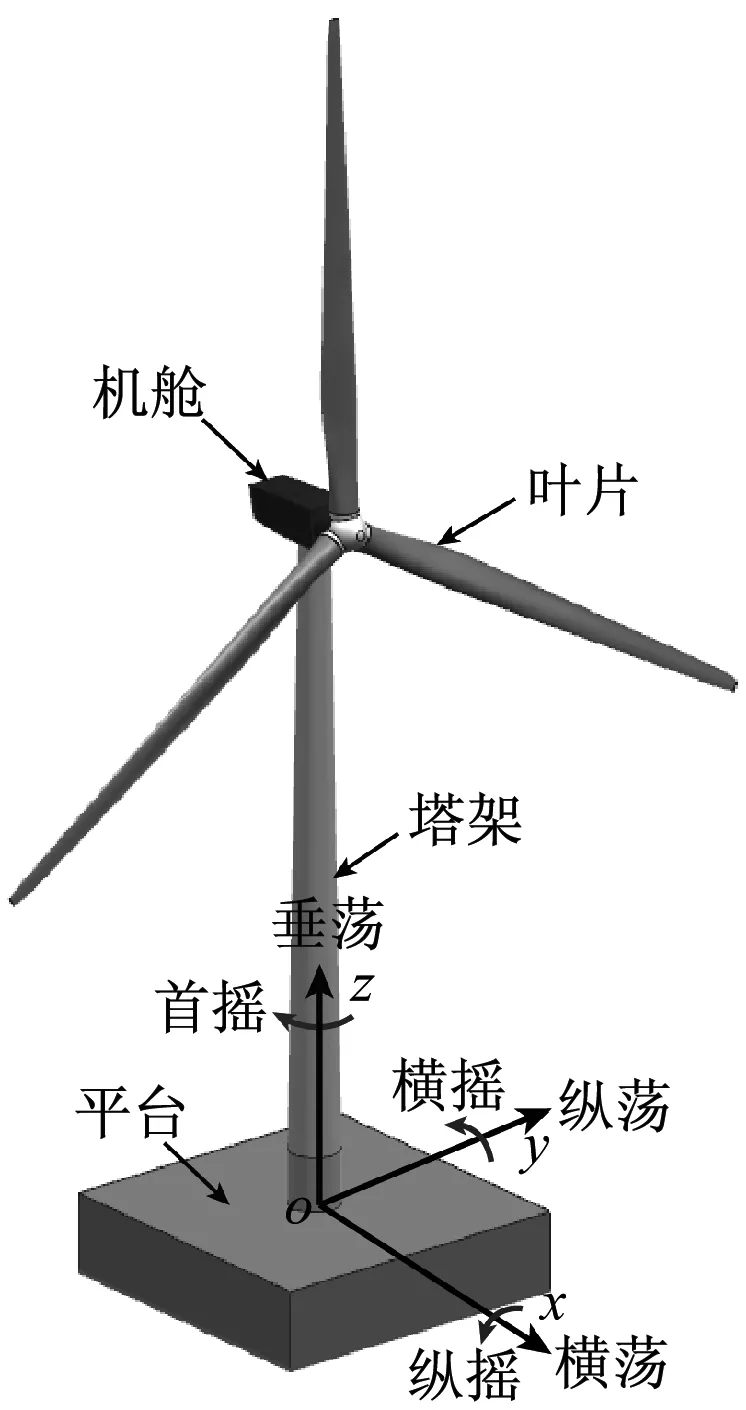
图1 Barge平台风力机模型及平台自由度示意图

TMD是由主结构和附加在主结构上的子结构组成的，其中子结构包括固体质量、弹簧减振器和阻尼器等，是一种效果显著的动力减振装置[16]，其较早地应用于高层建筑以减弱高空强风及台风吹拂造成的摇晃。TMD模型如图2所示。

图2 TMD模型示意图

图2中，m为调频质量阻尼器的固体质量；k为弹簧刚度；d为阻尼器的阻尼。

调谐质量阻尼器的工作机理为[17]：先计算出系统自振频率，将TMD的自振频率调谐至该自振频率，使结构在外部载荷作用下产生振动时，TMD系统也随之一起振动，其相对运动过程中产生的调谐惯性力反作用到结构上，然后通过阻尼构件将作用力耗散，使结构的振动幅值得到衰减，以达到结构稳定性控制的目的。

2 多岛遗传算法

多岛遗传算法(Multi-island genetic algorithm，MIGA)是在传统遗传算法基础上建立的一种基于群体分组的并行性遗传算法，与传统遗传算法相比，MIGA具有更优良的全局求解能力和更高的计算效率[18]。多岛遗传算法将整个种群分解成多个子群(这些子群被称为“岛”)，并将这些子群互相分离，隔绝于不同的“岛屿”上，对每个子群中的个体进行传统遗传算法操作(选择、杂交、变异)，使每个子群采用不同的进化机制独立地进化，并且各个“岛屿”间以一定的时间间隔进行“迁移”操作，使各个“岛屿”间进行信息交换。该算法保证了进化过程中优化解的多样性，从而有效抑制了早熟现象，有利于找到全局最优解。MIGA进化过程如图3所示，mi为迁移间隔，k为整数。

图3 多岛遗传算法原理图

MIGA反复地使用算子和选择原则，从亲代到子代再到孙代直至重孙代不停地繁衍，从而种群对环境的适应性不断得到提高。流程如下：

第1步：初始化群体；

第2步：计算个体的适应度函数值；

第3步：按个体适应度决定选择进入下一代的个体；

第4步：按概率Pc进行交叉操作；

第5步：按概率Pm进行突变操作；

第6步：若未满足停止条件，则转到第2步，否则进入第7步；

第7步：输出种群中适应度最优的染色体作为问题的最优解。

MIGA流程图如图4所示。

3 优化目标及约束条件

由于Barge型漂浮式风力机处于深海环境，在环境载荷共同作用下沿所设坐标系往复运动，因此笔者计算了漂浮式风力机的塔顶左右位移标准差σ1及平台横摇标准差σ2。

图4 多岛遗传算法流程图

目标函数：以σ1和σ2之和最小为目标函数。

约束条件：

质量m： 10 000 kg≤m≤40 000 kg

刚度k： 5 000 N/m≤k≤25 000 N/m

阻尼d： 6 000 N·s/m≤d≤21 000 N·s/m

优化设计所使用的MIGA控制参数中种群数、交叉概率、变异概率、迁移概率及最大代数分别为50、0.85、0.02、0.3和20。

4 计算工况

我国沿海海域频繁出现的海况为三级浪，有义波高Hs为0.50～1.25 m，极端海况下有义波高Hs为7.5 m[19]。

参考我国沿海海域频繁出现的海况又不失一般性，环境参数设定如下：1)波浪谱为P-M谱，有义波高为4.5 m，波浪周期为5 s；2)风谱为API谱，参考轮毂中心处风速为额定风速11.4 m/s；3)海流速度由海平面1.2 m/s至海底线性减小至0；4)风浪流均为垂直入射风力机风轮迎风面方向的最恶劣情况。

5 结果与分析

依据所设计的优化目标及MIGA参数设置方法，采用MIGA对计算结果进行优化，对质量、刚度及阻尼进行搜索寻优。

图5给出了塔顶左右位移标准差σ1随质量m、刚度k及阻尼d样本点分布的四维云图。图6给出了σ1随质量m变化的剖面图。由图5和图6可知，随着TMD质量增加，σ1变化较明显，呈现出先减小后增大的趋势，质量在15 000～25 000 kg内，σ1较小。将图6中质量为15 000～25 000 kg内的剖面图局部细化，得到图7所示部分剖面图。由图7可知，当质量在18 695～22 935 kg内时，塔顶左右位移标准差存在极小值；当阻尼取值不变时，σ1随刚度变化趋势较小，说明刚度变化对σ1影响不明显；当刚度取值不变，阻尼取值在12 000～17 000 N·s/m时，σ1存在明显变化。

图5 σ1四维图

图6 σ1剖面图

(1)m=16 575 kg

(2)m=18 695 kg

(4)m=22 935 kg

(5)m=25 055 kg

(6)m=27 175 kg

图8给出了平台横摇标准差σ2随质量m、刚度k及阻尼d样本点分布的四维云图。图9给出了σ2随质量m变化的剖面图。由图8和图9可知，随着TMD质量增加，σ2变化较明显，呈现出先减小后增大的趋势，质量在20 000～30 000 kg内时，平台的横摇标准差σ2较小。将该区域细化，得到如图10所示的局部剖面图。由图10可知，当质量取值在18 315～25 905 kg内时，平台横摇的标准差σ2存在极小值；当阻尼取值不变时，刚度变化对σ2影响较小；当刚度取值不变，阻尼取值在12 000～17 000 N·s/m时，σ2存在明显变化。

图8 σ2四维图

图9 σ2剖面图

(a)m=15 605 kg

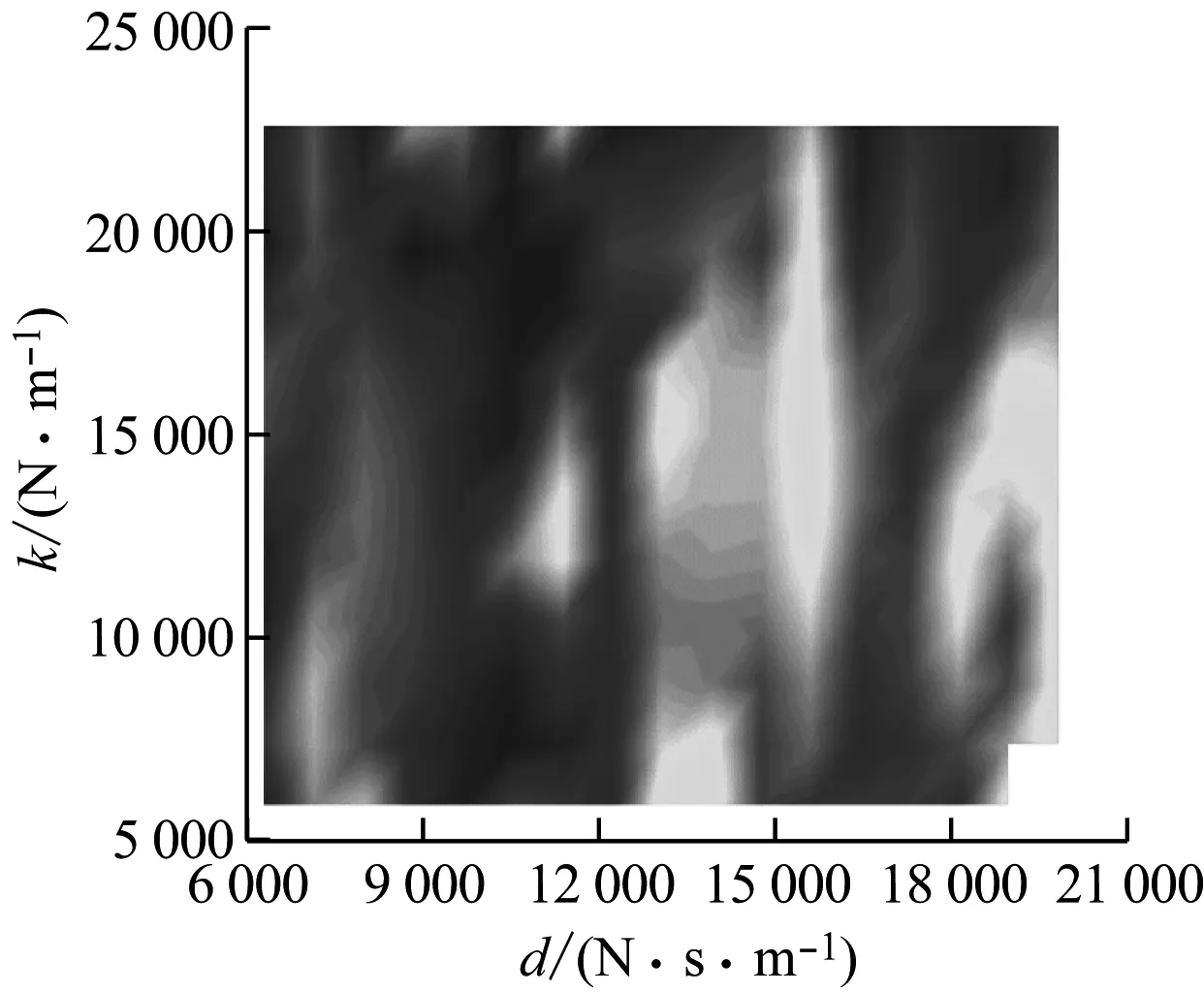
(b)m=18 315 kg

(c)m=21 025 kg

(d)m=23 735 kg

(e)m=25 905 kg

(f)m=28 615 kg

表1为MIGA优化后得到的TMD设计参数。

表1 MIGA优化结果

为验证优化算法结果的准确性，将TMD各参数按优化结果进行重新设置，计算结果如图11所示，其中传统TMD是指按照den Hartog原则[20]确定的TMD参数。

由图11(a)可知，在传统TMD参数控制下，平台的横摇均值减小到0.41°，波动范围由原来的-2°～2.5°减小到-1°～1.4°，在一定程度上减小了摇荡幅度；优化TMD控制下，平台的横摇幅度减小至0.16°，波动范围减小到-0.6°～1°。由计算结果可知，无控制、传统TMD和优化TMD的Barge平台横摇标准差分别为0.92、0.54和0.34，优化TMD分别是前两者的37%和63%，表明参数优化后TMD在横摇上具有显著的控制效果。由图11(b)可知，在传统TMD参数控制下，塔顶左右位移标准差均值为-0.052 m，波动范围为-0.1～0.02 m；TMD参数优化后塔顶左右位移标准差均值减小至-0.036 m，波动范围减小至-0.05～0 m。由计算结果可知，无控制、传统TMD和优化TMD的Barge平台塔顶左右位移标准差分别为0.048、0.03和0.02，优化TMD分别是前两者的42%和67%，表明参数优化后TMD对塔顶左右位移具有显著的控制效果。同时由上述计算结果验证了MIGA的有效性。

(a)横摇

(b)塔顶左右位移

6 结 论

(1)漂浮式风力机的塔顶左右位移及平台的横摇随TMD参数的变化趋势相似，随着TMD质量增加，均呈现出先减小后增大的趋势；当阻尼取值不变时，刚度变化影响不明显；当刚度取值不变时，阻尼存在一定变化。

(2)无控制、传统TMD和优化TMD的Barge平台横摇标准差分别为0.92、0.54和0.34，优化TMD分别是前两者的37%和63%，平台塔顶左右位移标准差分别为0.048、0.03和0.02，优化TMD分别是前两者的42%和67%，表明参数优化TMD对平台动态响应的抑制效果更优。

(3)通过与漂浮式风力机无控和受传统TMD控制的结果进行对比分析，验证了MIGA优化结果的有效性，为海上漂浮式风力机TMD参数确定提供了一定的理论参考。

：

[1] 丁勤卫, 李春, 王东华, 等. 螺旋侧板对漂浮式风力机平台动态响应的影响[J].动力工程学报, 2016, 36(8): 629-637, 657.

DING Qinwei, LI Chun, WANG Donghua, et al. Effects of helical strake on dynamic response of the platform for floating wind turbines[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(8): 629-637, 657.

[2] DING Qinwei, LI Chun.Research on the influence of helical strakes on dynamic response of floating wind turbine platform[J].ChinaOceanEngineering, 2017, 31(2): 131-140.

[3] JUNGINGER M, FAAIJ A, TURKENBURG W C. Cost reduction prospects for offshore wind farms[J].WindEngineering, 2004, 28(1): 97-118.

[4] 姜楠. 深海风力发电技术的发展现状与前景分析[J].新能源进展, 2015, 3(1): 21-24.

JIANG Nan.Analysis on status and prospect of wind power generation in deep sea[J].AdvancesinNewandRenewableEnergy, 2015, 3(1): 21-24.

[5] 丁勤卫, 李春, 叶柯华, 等. 风波流对多平台阵列浮式风机Spar平台运动特性的影响[J].农业工程学报, 2016, 32(21): 223-229.

DING Qinwei, LI Chun, YE Kehua, et al. Effect of wind, wave and current on movement characteristics of array of floating wind turbine Spar platform[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2016, 32(21): 223-229.

[6] JONKMAN J M. Dynamics modeling and loads analysis of an offshore floating wind turbine[D]. Boulder, USA: University of Colorado, 2007.

[7] MUSIAL W, BUTTERFIELD S, BOONE A. Feasibility of floating platform systems for wind turbines: preprint[R]. Golden, USA:National Renewable Energy Laboratory, 2003.

[8] 丁勤卫, 李春, 周国龙, 等. 陆海风力机动态响应对比[J].动力工程学报, 2016, 36(1): 65-73.

DING Qinwei, LI Chun, ZHOU Guolong, et al. Comparison of dynamic response between stationary and floating wind turbines[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(1): 65-73.

[9] NAMIK H, STOL K. Individual blade pitch control of floating offshore wind turbines[J].WindEnergy, 2010, 13(1): 74-85.

[10] FISCHER T, de VRIES W, RAINEY P, et al. Offshore support structure optimization by means of integrated design and controls[J].WindEnergy, 2012, 15(1): 99-117.

[11] DUNNE F, SIMLEY E, PAO L Y. LIDAR wind speed measurement analysis and feed-forward blade pitch control for load mitigation in wind turbines[R]. Golden, USA:National Renewable Energy Laboratory, 2011.

[12] 贾文强, 谢双义, 金鑫. 基于反馈控制策略的陆上与海上风力机塔架前后振动控制效果分析[J].西华大学学报(自然科学版), 2015, 34(6): 32-35, 46.

JIA Wenqiang, XIE Shuangyi, JIN Xin. The analysis of tower fore-aft vibration control effects for onshore and offshore wind turbines based on the feedback control strategy[J].JournalofXihuaUniversity(NaturalScience), 2015, 34(6): 32-35, 46.

[13] LACKNER M A, ROTEA M. Passive structural control of offshore wind turbines[J].WindEnergy, 2011, 14(3): 373-388.

[14] JONKMAN J, MATHA D. A quantitative comparison of the responses of three floating platforms[C]//ProceedingsofEuropeanOffshoreWind2009ConferenceandExhibition.Stockholm, Sweden:National Renewable Energy Laboratory, 2009.

[15] ROBERTSON A N, JONKMAN J M. Loads analysis of several offshore floating wind turbine concepts[C]//Proceedingsofthe21stInternationaloffshoreandPolarEngineeringConference.Maui,Hawaii, USA: International Society of Offshore and Polar Engineers, 2011.

[16] 阎石, 牛健, 于君元, 等. 风力发电机塔架结构减振控制研究综述[J].防灾减灾工程学报, 2016, 36(1): 75-83.

YAN Shi, NIU Jian, YU Junyuan, et al. Review of vibration control research of wind turbine tower structures[J].JournalofDisasterPreventionandMitigationEngineering, 2016, 36(1): 75-83.

[17] 王肇民. 高耸结构振动控制[M]. 上海: 同济大学出版社, 1997.

[18] 周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999.

[19] 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.

[20] den HARTOG J P. Mechanical Vibrations[M]. New York, USA:McGraw-Hill, 1956.