一种风电机组轴承健康劣化趋势预测方法
董兴辉, 张 光, 程友星, 王 帅
(1.华北电力大学 能源动力与机械工程学院,北京102206;2.河南理工大学 电气工程与自动化学院,河南焦作 454000)
风电机组运行环境恶劣,受气象等多种不确定因素的影响,容易出现性能与状态劣化,频繁出现故障。风电机组的关键部件一旦失效,检修时间较长,不仅影响发电量,也增加了风电场的运维成本[1-3]。风机轴承作为风电机组关键部件,在机组机械故障中占很高比例,发电机、齿轮箱的机械故障中约80%是由轴承失效而导致的[4]。较早掌握风电机组轴承的劣化程度和劣化趋势,实时了解风电机组状态,在可预知情况下合理安排检修,有助于提高整机的可靠性和利用率。
近年来,国内外学者针对风电机组轴承健康研究集中在劣化程度与状态评估2方面。安学利等[5-7]基于振动参数量计算风电机组主轴承、齿轮箱轴承和发电机轴承等的劣化程度;李辉等[1,8]基于温度参数量研究风电轴承劣化程度,并在此基础上进一步对轴承进行状态评估,但没有对机组轴承劣化发展趋势开展预测研究。
笔者基于数据采集与监视控制(SCADA)系统监测数据,应用改进的集合经验模态分解(EEMD)和时间序列神经网络,通过建立预测模型,研究风电机组轴承健康状态温度劣化趋势。首先,利用SCADA监测的有关参数(如风速、功率、发电机转速和环境温度等)与轴承温度的相关系数,归一化得到影响权重,基于温度特征量构建轴承健康劣化度模型;然后利用改进后的EEMD对劣化趋势进行分解,得到一系列相对平稳的本征模态函数(IMF)分量和一个剩余分量;最后,应用时间序列神经网络对各类分量建立预测模型,叠加所有预测分量,得到最终预测结果。
1 轴承健康劣化度模型
1.1 轴承劣化度
选用轴承运行温度参数作为风电机组健康装填评价指标,采用相对劣化度d′(t)来表征风电机组轴承当前的相对劣化程度,表达式如下:
(1)

1.2 轴承健康状态模型
轴承健康状态模型的建立如下。
(1) 样本数据。
SCADA数据中,与风电机组轴承温度相关的主要参数有风速、功率、发电机转速和环境温度[8]。从SCADA系统中选取n组健康的、同一时刻的轴承温度、风速、有功功率、发电机转速和环境温度历史数据,构建样本集{(Vi,Pi,Ni,Ti,环,Ti)},i=1,2,…,n,其中Vi表示风速,Pi表示有功功率,Ni表示转速,Ti,环表示环境温度,Ti表示轴承温度。
(2) 相关系数和权重。
相关系数C反映了变量X(V,P,N,T环)对Y(T)的相关程度,记作C(X,Y)。
(2)

将相关系数归一化处理后,得到变量X(V,P,N,T环)对Y(T)的影响权重A(a1,a2,a3,a4),其中:
(3)
式中:aj(Xj,Y)为第j类变量对Y(T)的影响权重;k为变量的总数,即k=4。
(3) 工况划分。

(4)
式中:σ为不同工况下温度偏离方差。
(4) 劣化度。

(5)
2 轴承健康劣化趋势预测
风电机组轴承健康劣化趋势具有明显的非平稳性特性,这直接影响到其预测精度,需要提前处理将劣化趋势分解成相对平稳的分量。
经验模态分解(EMD)可以将复杂的非平稳信号分解为一系列相对平稳的本征模态函数分量和一个剩余分量,一定程度上避免了人为因素对分解结果的干预。但在某些情况下,EMD会产生模态混叠,出现分解后有局部不平稳和不连贯现象,因此往往得不到理想的分解结果。EEMD加入高斯白噪声,利用高斯白噪声频率均匀分布的统计特性,使信号在不同尺度上具有连续性,避免了模态混叠现象[10-11]。
2.1 EEMD模态分解
将多组具有有限振幅的高斯白噪声序列ni(t)添加到原始劣化趋势上,共进行m次,即
di(t)=d(t)+ni(t),i=1,2,…,m
(6)
式中:di(t)为t时段第i次加入高斯白噪声后的劣化度。
对di(t)进行EMD分解,得到n个本征模态函数cij(t)和一个ri(t)。其中,cij(t)表示第i次加入高斯白噪声后,分解获得的第j个IMF,j=1,2,…,n。
将获得的IMF进行总体平均运算,得到基于EEMD的IMF:
(7)
2.2 改进的EEMD方法
由于风电机组轴承健康劣化趋势受各种噪声的影响,主要是随机噪声和脉冲噪声。而EEMD分解方法仅能去除信号中的随机噪声,脉冲噪声还有待处理。利用小波变换对信号进行去噪,能滤除高频噪声部分,重构低频部分,保留有价值的信息[12],因此在对信号进行EEMD分解之前需进行小波去噪。具体步骤如下:(1)选择合适的小波基,并确定分解层数n,然后对信号进行n层小波分解;(2)将高频系数全部置零;(3)对第n层的低频系数和第1~第n层经过阈值处理后的高频系数进行重构,得到去噪后的信号。
2.3 组合预测
分别叠加高频分量和低频分量得到组合高频信号和组合低频信号。应用时间序列神经网络模型对组合高频信号、组合低频信号和残余量进行预测,进一步叠加各预测结果得到最终预测结果(见图1)。
3 算法验证
3.1 数据准备
以华北某风电场56号风电机组的发电机后轴承为研究对象,该风机切入风速为3 m/s,切出风速为24 m/s。随机选择2015-06-01—2016-03-30采样频率为10 min的发电机后轴承温度、风速和有功功率的SCADA数据,筛选后共有32 595组健康的样本数据,如表1所示。
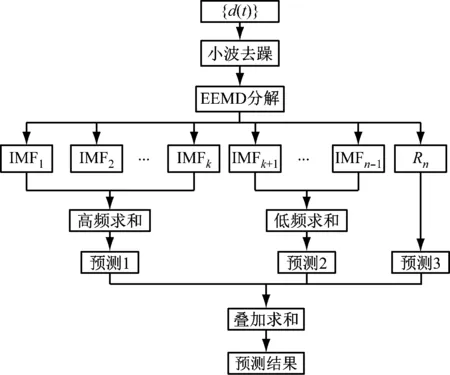
图1 改进的EEMD-时间序列神经网络组合预测流程图
Fig.1 Flow chart of improved EEMD-time series neural network combined forecasting
表1 健康数据集
3.2 相关性计算
应用式(2)计算各参数与轴承温度的相关系数,通过式(3)归一化处理后的各相关系数作为各变量影响轴承劣化度的权重,结果见表2。
3.3 健康状态劣化趋势
从32 595组样本数据中,选取32 395组数据作为建模样本,其余的200组数据作为测试样本。
表2各参数与轴承温度的相关系数
Tab.2Correlationcoefficientbetweeneachparameterandbearingtemperature

参数风速功率发电机转速环境温度C0.5570.5530.4530.136权重0.3280.3250.2670.080





图2 健康状态劣化趋势

图3 加权后健康状态劣化趋势
3.4 模态分解
从图3可以看出,风机轴承健康状态劣化趋势具有复杂的非平稳性,为了提高状态劣化趋势预测的准确性,利用改进的EEMD将其分解成若干个相对平稳的分量,分解结果见图4。图中c1~c6为不同尺度的较平稳的IMF,c7为趋势分量。
通过计算得到各个分量的均值(见表3)。从表3可以看出,各个分量的均值在c5处出现了较大的波动,有明显偏离0的趋势,因此c1~c4为高频分量,c5~c6为低频分量。
3.5 预测结果
时间序列神经网络模型能够较好地适应信号的非线性和非平稳性,具有较高的预测精度。因此,最终选择时间序列神经网络模型来获得各类组合分量的预测结果。







图4 基于改进的EEMD轴承健康状态劣化趋势分解结果
Fig.4 Decomposed results of degradation trend for wind turbine based on modified EEMD

表3 各个分量的均值
选用前160组数据进行训练和测试,后40组数据进行预测。各类组合分量分别进行时间延迟L=3的时间序列神经网络预测,组合高频信号、组合低频信号和残余量的预测结果如图5所示。从图5可以看出,随着轴承健康状态劣化度叠加分量的平稳性越好和规律性越强,预测精度越高。
将各分量的预测结果进行叠加,得到风机轴承健康状态劣化趋势的最终预测结果。并与其他的预测方法进行对比,结果如图6所示。由图6可知,所提出的预测模型可以有效跟踪风机轴承劣化趋势。
4 模型误差分析
采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)和均方根百分比误差(MSPE)等误差指标来度量模型精度。同时,也为了验证本文模型的准确性,分别采用人工神经网络(BPNN)模型、径向基函数神经网络(RBFNN)模型、支持向量机(SVM)模型和时间序列神经网络模型对不同机组的发电机后轴承健康状态劣化趋势进行预测,未改进的EEMD预测误差如表4所示。
由表4可知,单看MAE和RMSE 2个误差指标,对于未使用EEMD方法分解的预测模型,即BPNN模型、RBFNN模型、SVM模型和时间序列神经网络模型,通过对3台机组的发电机后轴承状态劣化趋势结果来看,时间序列神经网络模型误差都是最小的,说明对于较复杂的非线性和非平稳性信号,时间序列神经网络模型的预测精度相对其他传统预测模型更高。

(a) 组合高频信号预测结果

(b) 组合低频信号预测结果

(c) 残余量预测结果

图6 最终预测结果
而在使用EEMD方法分解之后,即EEMD+时间序列神经网络模型,3台机组的各项误差指标都有明显改善。从表4中的均值误差指标分析,EE-MD+时间序列神经网络模型的几个误差值相比时间序列神经网络模型降低了50%多,表明EEMD结合传统参数预测模型的组合预测能够有效提高预测精度。

表4 5种模型的误差指标
充分考虑小波去噪对信号的影响,分别对EEMD分解前的信号和EEMD分解后的各分量进行去噪,预测误差如表5所示。由表5可知,在对风机轴承健康状态劣化趋势进行EEMD分解之前进行小波去噪,能提高预测精度,而对EEMD的各分量进行小波去噪,并不能提高预测精度,反而在一定程度上降低了预测精度。
5 结 论
(1) 利用SCADA监测风速、功率、转速和环境温度参数,计算这些参数与轴承温度(劣化度)的相关系数,归一化处理记作该参数对轴承劣化度的影响权重。在此基础上,基于温度特征量构建的轴承健康劣化度模型,可有效描述轴承的劣化程度。
(2) 应用改进后的EEMD结合时间序列神经网络模型分析风机轴承健康状态劣化趋势,将具有非平稳性特性的劣化趋势分解为相对平稳和规律的分量。相对于其他预测方法多进行了2次预测,但能很好地跟踪劣化趋势,得到更高的预测精度。
表5改进的EEMD组合预测模型的误差指标
Tab.5ErrorindexesofmodifiedEEMDcombinedforecastingmodel

机组误差指标EEMD+小波小波+EEMD38号MAE0.03330.0171RMSE0.04590.0327MAPE0.11220.0614MSPE0.16550.126256号MAE0.02910.0091RMSE0.03610.0109MAPE0.06720.0215MSPE0.08640.026687号MAE0.02110.0066RMSE0.03840.0129MAPE0.22320.0661MSPE1.36560.1161均值MAE0.02780.0109RMSE0.04010.0188MAPE0.13420.0497MSPE0.53920.0896
(3) 改进的EEMD结合时间序列神经网络的组合预测模型,可更准确地预测风电机组轴承健康状态劣化趋势,有利于风电场制定检修策略和开展可靠性评估。
:
[1] 李辉, 胡姚刚, 唐显虎, 等. 并网风电机组在线运行状态评估方法[J].中国电机工程学报, 2010, 30(33): 103-109.
LI Hui, HU Yaogang, TANG Xianhu, et al. Method for on-line operating conditions assessment for a grid-connected wind turbine generator system[J].ProceedingsoftheCSEE, 2010, 30(33): 103-109.
[2] TCHAKOUA P, WAMKEUE R, OUHROUCHE M, et al. Wind turbine condition monitoring: state-of-the-art review, new trends, and future challenges[J].Energies, 2014, 7(4): 2595-2630.
[3] YANG Wenxian, TAVNER P J, CRABTREE C J, et al. Cost-effective condition monitoring for wind turbines[J].IEEETransactionsonIndustrialElectronics, 2010, 57(1):263-271.
[4] 苏连成, 李兴林, 李小俚, 等. 风电机组轴承的状态监测和故障诊断与运行维护[J].轴承, 2012(1): 47-53.
SU Liancheng, LI Xinglin, LI Xiaoli, et al. Condition monitoring and fault diagnosis and operating maintenance systems for wind turbine bearings[J].Bearing, 2012(1): 47-53.
[5] 安学利, 唐拥军, 王允. 基于健康样本的风电机组滚动轴承状态评估[J].中国水利水电科学研究院学报, 2015, 13(1):48-53.
AN Xueli, TANG Yongjun, WANG Yun. State evaluation of wind turbine roller bearing based on normal samples[J].JournalofChinaInstituteofWaterResourcesandHydropowerResearch, 2015, 13(1):48-53.
[6] 安学利, 唐拥军, 吴光军, 等. 基于健康样本的风电机组状态评估与异常检测系统[J].大电机技术, 2015(2):14-17.
AN Xueli, TANG Yongjun, WU Guangjun, et al. Condition assessment and anomaly detection system of wind turbine based on healthy samples[J].LargeElectricMachineandHydraulicTurbine, 2015(2):14-17.
[7] 滕伟, 姜锐, 张阳阳, 等. 基于多尺度包络谱图的直驱式风电机组轴承故障特征提取[J].动力工程学报, 2017, 37(5): 373-378.
TENG Wei, JIANG Rui, ZHANG Yangyang, et al.Bearing fault feature extraction for a direct drive wind turbine using multi-scale enveloping spectrogram[J].JournalofChineseSocietyofPowerEngineering, 2017,37(5): 373-378.
[8] 李辉, 胡姚刚, 李洋, 等. 基于温度特征量的风电机组关键部件劣化渐变概率分析[J].电力自动化设备, 2015, 35(11): 1-7, 19.
LI Hui, HU Yaogang, LI Yang, et al. Gradual deterioration probability analysis based on temperature characteristic parameters for critical components of wind turbine generator system[J].ElectricPowerAutomationEquipment, 2015, 35(11): 1-7, 19.
[9] 刘长良, 闫萧. 基于工况辨识和变分模态分解的风电机组滚动轴承故障诊断[J].动力工程学报, 2017, 37(4): 273-278, 334.
LIU Changliang, YAN Xiao. Fault diagnosis of a wind turbine rolling bearing based on variational mode decomposition and condition identification[J].JournalofChineseSocietyofPowerEngineering, 2017, 37(4): 273-278, 334.
[10] 王贺, 胡志坚, 张翌晖, 等. 基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J].电工技术学报, 2014, 29(4): 237-245.
WANG He, HU Zhijian, ZHANG Yihui, et al.A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(4): 237-245.
[11] AN Xueli, JIANG Dongxiang, LI Shaohua, et al. Application of the ensemble empirical mode decomposition and Hilbert transform to pedestal looseness study of direct-drive wind turbine[J].Energy, 2011, 36(9): 5508-5520.
[12] 崔玉敏, 和卫星, 高彩虹. 基于小波变换及HHT的轴承故障诊断应用研究[J].计算机仿真, 2010, 27(10): 294-296, 300.
CUI Yumin, HE Weixing, GAO Caihong. Application of bearing fault diagnosis based on wavelet and HHT[J].ComputerSimulation, 2010, 27(10): 294-296, 300.

