利用截止期感知的云计算调度方法*

马振峰， 李松松

(大连海洋大学 信息工程学院，辽宁 大连 116300)

大数据的发展使得云计算面临着数据规模庞大的问题，云工作流调度已经成为一个重要的研究课题[1-2],它关系到云计算的成本和效率.但在现实中，工作流调度是一个NP难题，它不可能在多项式时间内产生最优解[3].随着智能计算算法的发展，采用蚁群算法、遗传算法、粒子群优化算法等智能计算算法来解决云计算工作流调度问题得到了普及[4-6].文献[7]使用工作流的动态关键路径来找到一个解.文献[8]提出了一个动态的工作流调度方法，使用能够找到最经济和实用资源的方法，并将几个任务合并成一个单一任务.文献[9]使用各种动态和静态算法来生成一个能够满足用户服务质量的解决方案.文献[10]开发了一个能够满足期限约束和最小化成本的约束模型，该模型是基于粒子群优化方法实现的.

本文提出一种利用截止期感知的云计算调度方法，将VM分配给需要调度的工作流，并在处理时间截止期完成工作的调度.实验研究表明，提出的算法在求解最小成本和期限约束模型方面优于粒子群优化方法.

1 理论基础

1.1 成本最小化和期限约束模型

定义总的执行成本(TEC)和总的执行时间(TET)如下：

(1)

式中，ETti表示调度任务完成的时间，Crj表示单位成本，LSTrj和LETrj分别表示资源rj的开始以及结束时间.另外，本文设置以下约束条件，以达到任务调度时间和成本的最小化.

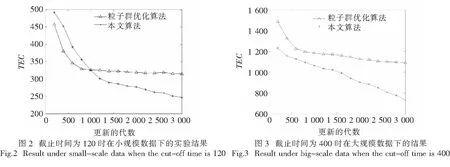
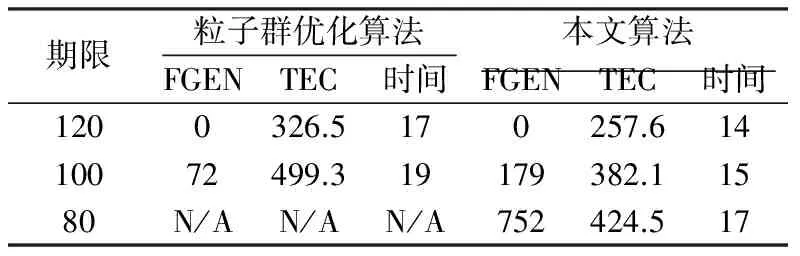
MinimizeTEC，TET

(2)

1.2 粒子群优化框架

在粒子群优化中，每一个粒子有两个向量x和v.x代表粒子的位置，也是所定义问题的一个解.v决定了在所定义的问题空间中粒子的运动.每个粒子的最佳位置pBest和种群的最佳位置gBest将存储和更新.对于每个粒子i，每一代的x和v的更新如式(3)和(4)所示：

(3)

(4)

式中d代表向量的维度，w是惯性权重，c1和c2是加速系数.r1和r2为0～1之间的随机数.在每一代中，评估每个粒子的适应度,更新它们的个体最佳位置和种群的最佳位置.最后，根据式(3)和(4)更新每个粒子的x和v.

2 利用截止期感知的云计算调度方法

提出的基于截止期限感知的调度策略中，调度程序从不同的用户处接受任务请求，将虚拟机作为资源分配给不同的请求，并借助遗传算法来共同完成任务.

2.1 具体算法介绍

rn表示第n个任务调度请求，tn1和tn2分别表示使用VM1和VM2完成调度任务rn所需的时间，dwn和drn分别表示调度任务rn的等待时间的截止期限和响应时间的截止期限，sn和cn分别表示在使用VM1和VM2上任务rn的开始时间.当调度任务开始时，算法利用解向量SV存储作业请求的调度序列，并且识别出最短的tn1和tn2.如果最短时间为tn1，则将它对应的调度任务rn加入SV的最前端，如果最短时间为tn2，则将它对应的调度任务rn加入SV的尾端.

假设存在p个实例来完成调度任务，则解向量SV可以表示为p个子序列：

S1={ri/(imodp)=1}，S2={ri/(imodp)=2}，…，Sp={ri/(imodp)=0}，

式中：1 ≤i≤n，并且每个子序列Si将依次在VM1、VM2上处理.

在产生p个子调度序列后，利用启发式方法来减少超时.文献[11]提出的遗传算法是一个模仿自然选择过程的启发式搜索.它可以根据选择、交叉和突变应用到优化问题中.本文利用遗传算法来优化执行时间以减少超时.

(1) 编码.编码种群的染色体的方法与粒子群优化方法相似，唯一的区别是本文使用整数而不是浮点数.坐标i的值代表ti运行的资源.例如，dimj=j表示ti运行在资源rj上.

(2) 选择.本文希望最小化成本，使用1/TEC来评估染色体的适应度.公式如下：

(3) 交叉和突变. 每个染色体交叉的概率为Pc.如果满足条件Random(0,1)

(4) 保持最好的策略. 文献[12]提出了保持在选择之前时间段内的最优解以避免破坏在突变或交叉中最好的染色体.在本文的方法中，假设有一个全局最优染色体，在每一代的运行过程中，如果存在比全局最优染色体更好的局部最优染色体，则用这个局部最优替代全局最优.提出的算法流程如图1所示.

3 实验结果分析

3.1 实验设置

使用不同规模的数据来进行实验.如果算法运行的代数FGEN>100 000，我们就可以认为解不存在；否则，当找到可行解后，继续执行3 000次运算，以寻找最优解.令Time表示算法执行的时间，比较在不同期限约束下粒子群优化和本文算法的FGEN和TEC.

在粒子群优化方法中，本文设置c1=c2=2.0,w=0.5，种群规模为100，遗传算法的种群规模也设置为100.对于遗传算法的交叉和突变概率，分为两种情况：(1) 当寻找到可行解时，设置Pc=0.15，Pm=0.008；(2) 反之，则令Pc=0.8，Pm=0.002.为了防止偶然性，本文将两种算法分别执行50次.

3.2 结果分析

首先，在小规模的数据上验证两种算法的性能.假设调度任务的数量为50个，资源数量为15种.3个截止时间设置成80、100和120.表1和图2所示为本次实验结果.在相同的条件下，本文算法的TEC值和计算时间相对于粒子群优化算法而言更小.在表1中，刚开始时，期限约束大，两种算法获得的可行解FGEN=0.但当截止时间变得越来越小，粒子群算法的收敛速度变得比本文算法更快.然而，当截止时间变得严格时，如80时，使用粒子群算法获得的可行解的数量为0，相比之下，本文算法却依旧能够获得多个可行解.

表1 小规模数据下FGEN和TEC不同的期限约束

其次，在小规模的数据上验证两种算法的性能.假设调度任务的数量为100个，资源数量为30种.3个截止时间设置成200、300和400.表2和图3所示为本次实验结果.同样的，由实验结果可知，尽管截止时间不同，由本文算法得出的可行解的计算时间总是比粒子群优化更少，本文算法具有更好的性能.

表2 大规模数据下FGEN和TEC不同的期限约束

4 结 论

提出了一个利用截止期感知的云计算调度方法来解决云计算环境中的资源调度问题.该算法能够在处理时间截止期完成工作的调度，并且采用遗传算法来优化执行时间以减少超时，同时还能够优化任务调度的执行成本.在不同调度规模和不同期限约束下的实验表明，提出的算法更能适应各种期限的约束，能够以比粒子群优化更小的TEC找到一个更优解.

参考文献

[1] 李敬伟, 张皓, 赵丽. 基于改进群搜索优化算法的云计算任务调度方案[J]. 湘潭大学自然科学学报, 2017, 39(4): 99-102.

[2] ZHANG Y Q, WANG X F, LIU X F, et al. Survey on cloud computing security[J]. Journal of Software, 2016, 8271(1):302-311.

[3] FANG W, MEI′AN L I, DAUN W. Cloud computing task scheduling based on dynamically adaptive ant colony algorithm[J]. Journal of Computer Applications, 2013, 33(11):3160-3159.

[4] 曾芳桂,赵曼.体育联赛中基于GSO算法的赛程优化方法[J]. 湘潭大学自然科学学报, 2018, 40(1): 72-76.

[5] BHARATHI C, REKHA D, VIJAYAKUMAR V. Genetic algorithm based demand side management for smart grid[J]. Wireless Personal Communications, 2017, 93(2):481-502.

[6] 王东风, 孟丽. 粒子群优化算法的性能分析和参数选择[J]. 自动化学报, 2016, 42(10):1552-1561.

[7] LIU X F, ZHAN Z H, DU K J, et al. Energy aware virtual machine placement scheduling in cloud computing based on ant colony optimization approach[C]// Conference on Genetic and Evolutionary Computation. ACM, 2014:41-48.

[8] CHEN W N, ZHANG J. An ant colony optimization approach to a grid workflow scheduling problem with various QoS requirements[J]. IEEE Transactions on Systems Man & Cybernetics，Part C, 2009, 39(1):29-43.

[9] MAO M. Auto-scaling to minimize cost and meet application deadlines in cloud workflows[C]// High PERFORMANCE Computing, Networking, Storage and Analysis. IEEE, 2011:1-12.

[10] MALAWSKI M, JUVE G, DEELMAN E, et al. Algorithms for cost- and deadline-constrained provisioning for scientific workflow ensembles in IaaS clouds[C]// International Conference for High PERFORMANCE Computing, Networking, Storage and Analysis. IEEE Computer Society, 2012:1-11.

[11] ZHAN Z H, ZHANG J, LI Y, et al. Orthogonal learning particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(6): 832-847.

[12] ZHANG J, ZHAN Z H, LIN Y, et al. Evolutionary computation meets machine learning: a survey[J]. IEEE Computational Intelligence Magazine, 2011, 6(4): 68-75.