动车组隔振器结构对垂向刚度影响的研究

□ 汪 浩 □ 张立民

西南交通大学 牵引动力国家重点实验室 成都610031

1 研究背景

随着2017年6月26日“复兴号”动车组在京沪铁路的正式载客运行，标志着我国具有了完全自主知识产权的高速动车组列车。动车组技术中非常重要的一项指标是高速、平稳安全的运行。其中，车下设备在动车组高速运行时，因自身的转动、轮轨激励，以及其它设备的干扰等产生的振动，都会通过车体底架传递到车厢地板，影响运行安全性、平稳性。因此车下设备与车体底架相连的隔振器就显得非常重要［1］。实际上车下设备与车体底架之间的空间非常有限，因此隔振器结构参数的选择会受到一定限制。

笔者主要研究分析某型动车组车下设备使用的V形隔振器结构参数对隔振器垂向刚度的影响。通过ABAQUS有限元软件计算了隔振器多组结构参数的垂向刚度，分析结构参数对垂向刚度的影响，为在工程实际中对隔振器在安装空间有限的情况下的结构参数选择提供参考。

2 隔振器三维模型和有限元模型

2.1 三维模型

通常，对于隔振器的实体模型在计算前要做相应的简化，使模型在不影响整体计算结果的同时，又能达到简化计算的目的。笔者计算的参数是隔振器垂向刚度，因此可将隔振器对垂向刚度影响较小的结构参数进行简化，如金属骨架的平面和安装座倒角的去除，安装座的安装孔简化省略，以及对金属骨架中间安装孔的简化。隔振器三维模型如图1所示。

2.2 有限元模型

隔振器的垂向刚度是笔者分析的主要参数，在有限元分析计算时，影响隔振器垂向刚度的主要因素是橡胶材料的性能。橡胶材料在拉伸、压缩的时候具有三重非线性［2-3］：①几何非线性，橡胶材料挤压变形时，橡胶材料的位移量和变形量之间是非线性的，其计算方法比较复杂；②材料非线性，橡胶材料是超弹性材料，在受到拉压时，其力与位移之间的关系也是非线性的，且在变形后体积几乎不变，为近似不可压缩性材料；③边界状态非线性，隔振器的橡胶材料与金属垫片、安装座、金属骨架的接触是通过硫化粘合固定的，属于复杂的接触计算，也属于非线性的。

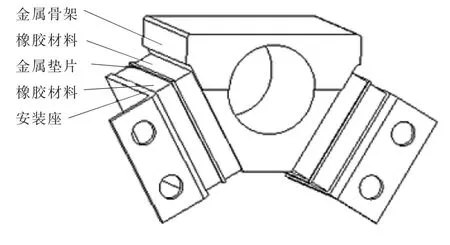
▲图1 隔振器三维模型

由此，在有限元分析计算时，需对模型作合理假设：①橡胶材料受到拉伸、压缩时的各向同性［4］；②橡胶材料拉伸、压缩时体积不变［5］；③金属垫片、金属骨架和安装座的刚度远远大于橡胶材料，可看作刚体，其形变量相对橡胶材料可忽略不计；④金属垫片、金属骨架、安装座与橡胶材料在粘合处看作是没有相对位移的整体。

隔振器模型在HYPERMESH前处理软件中划分网格时，采用的均是六面体八节点的单元格划分，在ABAQUS有限元软件中对应的单元类型为C3D8I。橡胶材料为体积不可压缩性材料，其单元格算法选择混合单元计算法。橡胶材料与金属垫片、金属骨架、安装座共八个接触面定义均为绑定约束，保证接触面没有相对位移。边界条件是对安装座底面及与之垂直面的节点全约束，不允许有位移和转动。载荷为施加在金属骨架的平面节点集中力，方向竖直向下。整个模型网格划分的单元格共有79 932个，节点89 988个。隔振器有限元网格模型如图2所示。

▲图2 隔振器有限元网格模型

3 橡胶材料常数确定

3.1 橡胶材料本构模型

在有限元计算中，橡胶材料有许多不同的本构模型，基于笔者分析的橡胶材料在应用中形变量在25%之内，属于橡胶材料的小变形，选择常用的穆尼·里夫林本构模型［6］可较准确描述橡胶材料的特性。橡胶材料本构模型应变能密度函数表达式为［7］：

式中：W为应变势能；I1、I2为变形张量；C1、C2为橡胶材料常数。

通常橡胶材料常数需试验获得。试验需要取相应的橡胶材料试样做拉伸、压缩、剪切等力学试验［8］，获得一系列橡胶材料的力-位移数据，然后再通过数据拟合得到所需要的常数。然而橡胶材料拉伸、压缩试验时间较长，材料自身对温度、湿度等外界环境敏感，使得试验自身的操作难度较大，得出的数据准确性也会受到一定的影响。

3.2 橡胶材料常数的估算

对橡胶材料常数的获取，试验是相对可靠的方法，可是试验过程较复杂，对于很多前期仿真计算显然不合适。在文献［9］中通过试验、仿真数据对比，当橡胶材料的肖氏硬度HS在50～70之间，形状为规则的天然橡胶时，在小变形情况下，橡胶材料常数C2/C1比值取0.2、0.25、0.4时计算出的橡胶材料刚度与试验测出的刚度误差较小，可作为仿真计算时的参考。

在将橡胶材料看作理想的体积不可压缩、小应变时，弹性模量E0、剪切模量G与材料常数的关系式为［10］：

橡胶材料的弹性模量E0和硬度的关系式为：

由式（2）、式（3）可以得到：

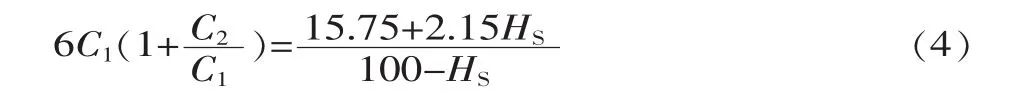
式中：HS为肖氏硬度值。

通过测出橡胶材料的硬度值，由式（4）与给出的C2/C1比值，即可计算得到C1、C2的值。

笔者所用隔振器的两个橡胶材料常数比值取C2/C1=0.25，橡胶材料硬度取肖氏硬度HS 60，得出材料常数的估算值为C1=0.482 5、C2=0.120 6。

4 计算结果与分析

笔者主要计算分析金属垫片厚度、橡胶材料厚度、金属骨架倾角（图3中的α角）对隔振器垂向刚度的影响。计算中，金属垫片、金属骨架和安装座材料均为QT550球墨铸铁，取弹性模量为150 GPa，泊松比为0.3。

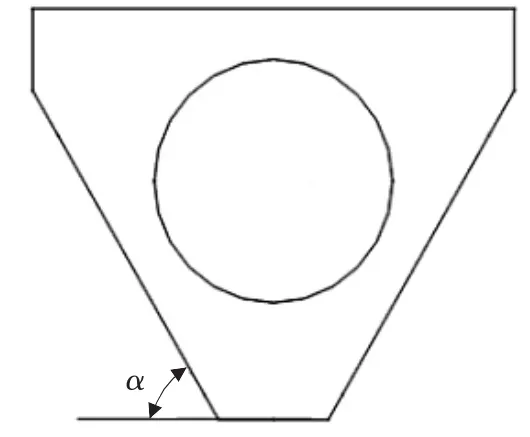
▲图3 金属骨架倾角示意图

4.1 金属垫片厚度对隔振器垂向刚度影响

隔振器金属垫片的厚度为2.5 mm，为计算其厚度对隔振器垂向刚度的影响，保证橡胶材料厚度为15 mm，金属骨架倾角为60°不变，设置间隔0.5 mm共九组不同厚度金属垫片，计算在相同载荷作用下的隔振器垂向刚度，见表1。绘制金属垫片的厚度与隔振器垂向刚度关系，如图4所示。

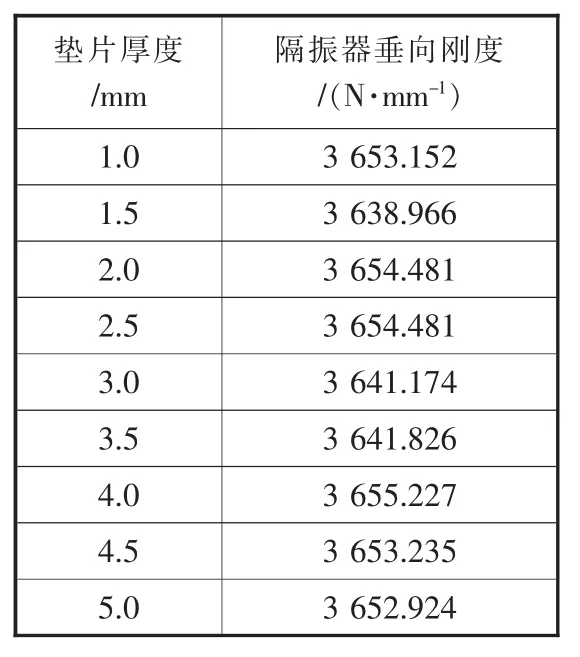
表1 不同厚度金属垫片在相同载荷下隔振器垂向刚度

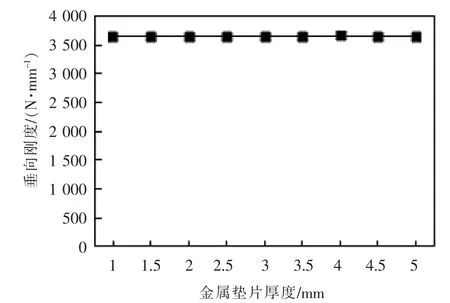
▲图4 金属垫片厚度与隔振器垂向刚度关系

由表1和图4可知，金属垫片厚度不同，对隔振器垂向刚度变化的影响较小。其中最大刚度与最小刚度值相比变化量不到1%。所以可认为，金属垫片的厚度在一定范围内对隔振器的垂向刚度几乎没有影响。

4.2 橡胶材料厚度对隔振器垂向刚度影响

隔振器用四块厚度均为15 mm的橡胶材料。为计算橡胶材料厚度对隔振器垂向刚度的影响，保证金属垫片的厚度为2.5 mm，金属骨架倾角为60°不变，设置七组不同厚度的橡胶，计算在相同载荷下隔振器垂向刚度，见表2。

由图5可知，随着橡胶材料厚度变厚，隔振器的垂向刚度有明显变化，变化趋势越来越小。因此可知，隔振器的垂向刚度随橡胶材料厚度增厚而变小。

4.3 金属骨架倾角对隔振器垂向刚度影响

金属骨架的倾角为60°，为得到倾角对隔振器垂向刚度的影响，保证金属垫片的厚度为2.5 mm、橡胶材料厚度为15 mm不变，设置七组不同倾角，计算在相同载荷下隔振器垂向刚度，见表3。

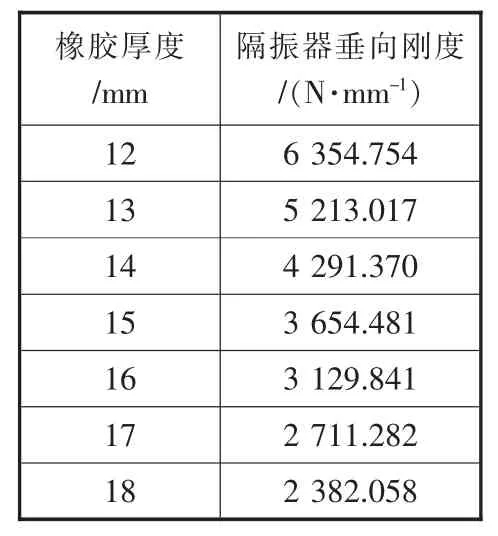
表2 不同厚度橡胶在相同载荷下隔振器垂向刚度

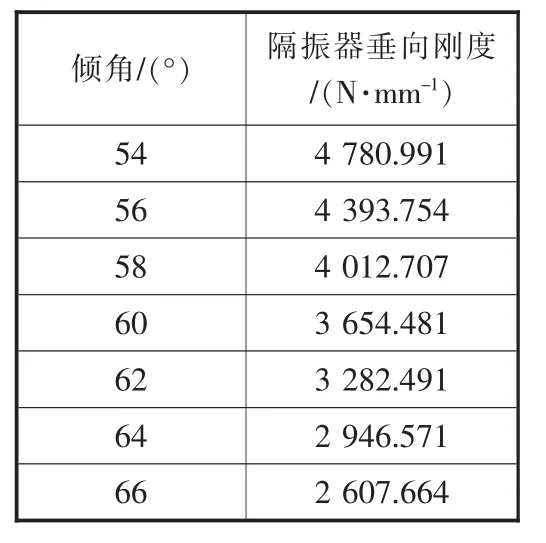
表3 不同金属骨架倾角在相同载荷下隔振器垂向刚度

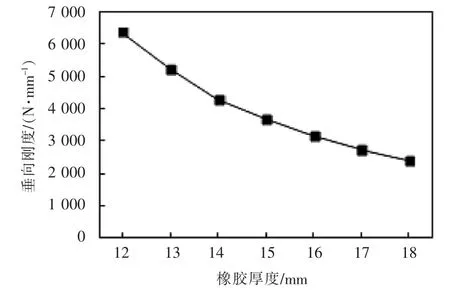
▲图5 橡胶厚度与隔振器垂向刚度关系

由图6可以看出，随着金属骨架倾角的变化，隔振器的垂向刚度变化明显，且隔振器垂向刚度随金属骨架倾角变大而减小。

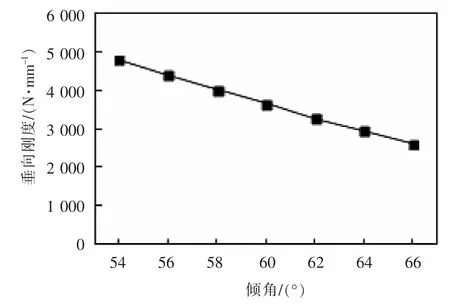
▲图6 金属骨架倾角与垂向刚度关系

5 与CRH3动车组V形减振器对比

笔者分析的隔振器与CRH3型动车组上V形橡胶减振器外形（图7）类似，都是在金属骨架上加载荷，橡胶材料斜置于金属骨架斜面上，用于减小减振器垂向空间，不同的是笔者分析的隔振器在两边的橡胶材料之间各有一块金属垫片，没有金属下骨架，安装座直接与橡胶材料相连，可更加减小隔振器的垂向空间。

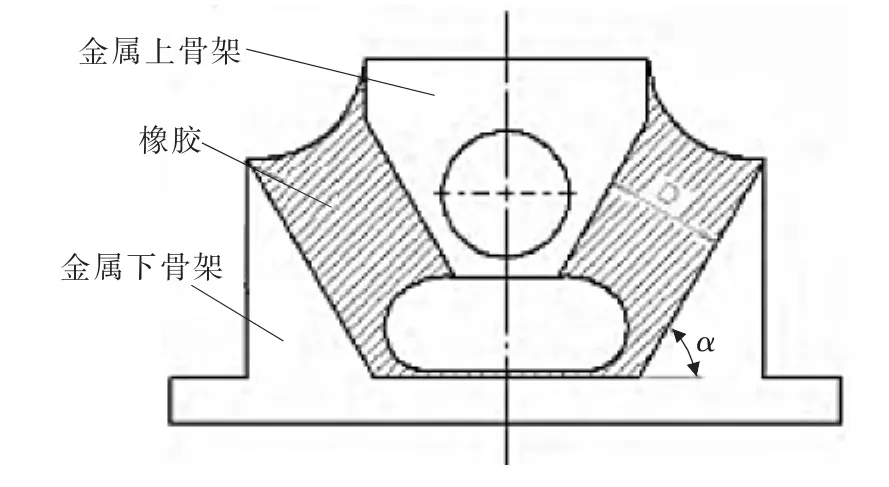
▲图7 CRH3型动车组V形减振器模型

笔者分析的隔振器与图7所示的V形减振器主要区别是在橡胶材料中有金属垫片，由4.1节计算知道，金属垫片自身的厚度在一定范围内对隔振器垂向刚度几乎没有影响。若是当金属垫片厚度为零时，其隔振橡胶部分的结构就与图7所示的V形减振器较为接近。在没有CRH3型动车组减振器具体参数的情况下，可以将橡胶材料中有无金属垫片作为CRH3型动车组V形减振器与笔者分析的隔振器在橡胶材料结构上的最大差异。保证金属骨架倾角为60°，分别在有金属垫片（厚度为2.5 mm）、无金属垫片（厚度为0）时，设置七组不同橡胶材料厚度，计算共十四组参数的隔振器垂向刚度，以及有金属垫片相对无金属垫片隔振器垂向刚度的增加比例即相对变化量，具体见表4。

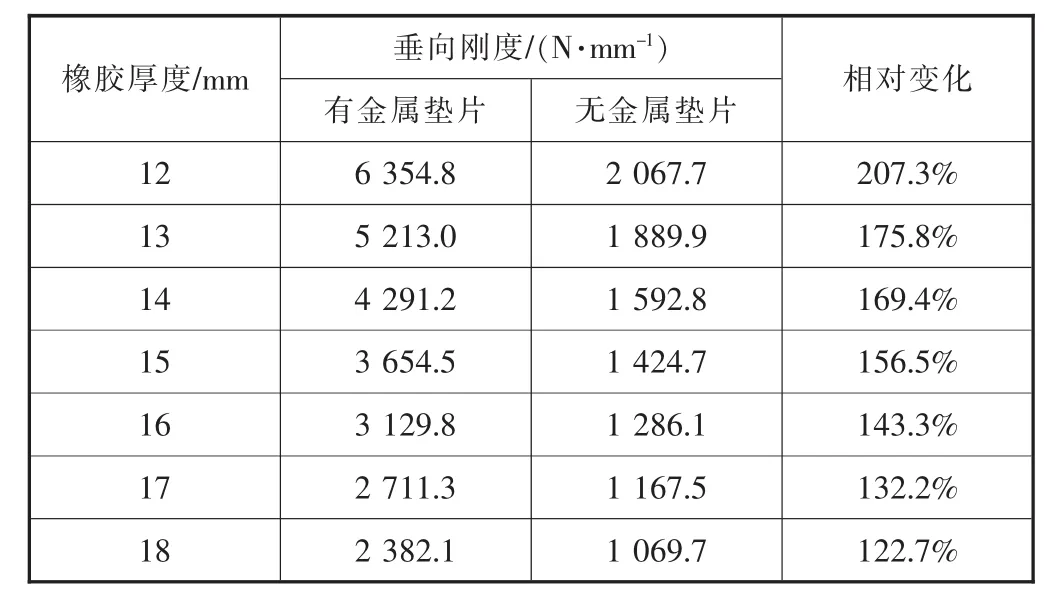
表4 有无金属垫片时不同厚度橡胶材料隔振器垂向刚度

由表4可以看出，在橡胶材料中有金属垫片比没有金属垫片时，隔振器的垂向刚度明显增大很多，最少也增大了122.7%，最大增大了207.3%。由此可见，在橡胶材料一定厚度范围内，在橡胶材料中加金属垫片可以明显增大隔振器的垂向刚度。

6 结束语

（1）通过计算分析，金属垫片厚度在一定范围内变化，相对隔振器垂向刚度的变化几乎可以忽略，所以可得金属垫片厚度对隔振器垂向刚度的影响很小。

（2）橡胶材料厚度增厚，隔振器垂向刚度随之越来越小，且厚度的变化对隔振器垂向刚度影响较大。

（3）金属骨架倾角变大，隔振器垂向刚度随之越来越小，且金属骨架倾角变化对隔振器垂向刚度的影响小于橡胶材料厚度对隔振器垂向刚度的影响。

（4）与CRH3型动车组V形减振器的结构对比中，发现在橡胶材料中加金属垫片可以显著地增大隔振器垂向刚度，因此，笔者分析的隔振器垂向刚度可调节范围更大。