深厚覆盖层上沥青混凝土心墙坝坝基廊道应力变形规律影响因素研究

白新革，何蕴龙，邢丽曼，王 竞

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2. 珠海华发实业股份有限公司，广东 珠海 519020)

0 引 言

近年来，越来越多的高心墙土石坝建立在深厚覆盖层上，廊道—防渗墙型式的防渗系统也应用得比较广泛，已采用类似连接形式的工程有长河坝水电站、硗碛水电站、瀑布沟水电站、金平水电站工程等[1]。然而，目前对心墙坝坝基廊道的应力变形的深入研究分析却并不多，在用有限元法进行土石坝结构计算分析时，有必要对廊道及其周边应力变形规律进行详细分析。由于覆盖层结构松散，压缩性大，对坝基廊道应力变形的影响不容忽视。廊道的跨度随河谷宽度变化而变化，尤其是廊道河床段的应力变形产生较大影响。廊道两岸岩台搁置段长度不同时，两岸约束作用也随之改变，从而对廊道，尤其是两岸岩台边缘附近的应力变形规律，产生一定影响。本文分别对这三个工程条件对坝基廊道应力变形的影响展开详细分析。

1 典型坝型概况

西南地区某沥青混凝土心墙堆石坝，坝高100 m。大坝防渗系统由沥青混凝土心墙、坝基廊道及防渗墙组成，廊道与防渗墙的连接采用刚性接头，廊道断面采用城门洞型，内尺寸3 m×3.5 m，外尺寸6 m×8 m，河床段长约150 m，廊道左、右岸深入基岩，分别形成长10 m的岩台段。覆盖层厚60 m，坝基混凝土防渗墙厚1.2 m，采用全封闭防渗。

2 计算原理和模型

2.1 子模型法

堆石坝坝基防渗系统中存在廊道与心墙、防渗墙、坝肩灌浆平洞的接头等多个细部构造，这些部位构造尺寸与大坝整体尺寸相差悬殊，材料分区也较为复杂，将其与大坝整体同时进行有限元分析具有一定的计算难度，因此本文采用了子模型法进行计算分析。

子模型方法又称切割边界位移法，该方法基于圣维南原理，先进行整体结构的分析，之后在整体模型中切割出一块区域重新进行计算，区域边界条件采用整体模型中相应位置的位移计算结果[2]。

有限元计算方程组为：

(1)

把它展开，即得：

K12δ2=F1-K11δ1

(2)

K22δ2=F2-K21δ1

(3)

式中：K为总刚度矩阵；δ为待求的位移分量；F为外荷载向量。由此知，特定的位移δ1可作为求未知的δ2的已知条件。根据此原理，子模型技术得以实现。对切割出来的细部进行网格加密，然后单独计算，整体模型为子模型提供边界上位移约束，满足了计算精确度的要求。

2.2 接触面模型

本文在模拟不同材料的分界面时，例如廊道两岸平洞接缝、防渗墙周边泥皮、残渣等采用薄层单元。采用S.C. Bandis岩石节理法向变形双曲线模型来确定薄层单元法向应力、应变关系[3,4]：

(4)

式中：δn为法向正应力；ΔVj为法向变形；a为1/Kni；a/b为应力、应变双曲线渐近线，即法向最大压缩量Vm，法向弹模表达式为：

(5)

采用Clough剪切双曲线模型来确定薄层单元切向应力应变关系：

(6)

式中：τ为切向剪应力；dh为剪切破坏前剪切变形；常数n为τ-dh双曲线水平渐近线的倒数；常数m为初始剪切刚度的倒数，按Mohr-Coulomb定律计算τp=C-tanφ·σn可得切向弹模表示如式：

2.3 有限元模型及相关参数

图1为有限元整体模型和子模型，整体模型上、下游侧边界距坝坡均为1倍坝高；左右岸距坝肩均1倍的坝高，底部施加全约束，四周施加法向约束，整体模型共有18 132个结点，15 938个单元。坝基廊道有限元子模型的边界上、下游距坝轴线均为40.0 m；从河床段坝底高程1 400 m垂直向上35.60 m，垂直向下距坝底40.0 m；两岸岸坡取至基岩范围，包含19 955个结点，18 592个单元。

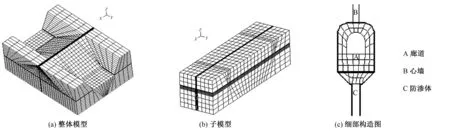
图1 三维有限元模型实体网格图Fig.1 Finite element mesh model

混凝土和基岩均采用线弹性模型，廊道混凝土和防渗墙混凝土弹性模量均为30 GPa，泊松比均为0.167，混凝土密度均为2 400 kg/m3。坝体材料及覆盖层的本构关系采用Duncan-Chang双曲线E-μ模型[4]，其材料参数见表1，接触面节理单元参数见表2。Duncan模型参数由三轴试验获得，混凝土与泥皮的接触面参数主要由直剪试验所得，其他接触面参数按经验选取。

3 坝基廊道应力变形影响因素规律研究

根据同类工程资料，在不同工程条件下，坝基廊道表现出不同的应力变形规律，本文分别针对覆盖层厚度、河谷宽度和廊道两岸搁置段长度三个工程条件对坝基廊道应力变形的影响展开详细分析[5-10]，典型剖面示意图如图2所示。

表1 E-μ模型参数Tab.1 Material parameters of the E-μ model

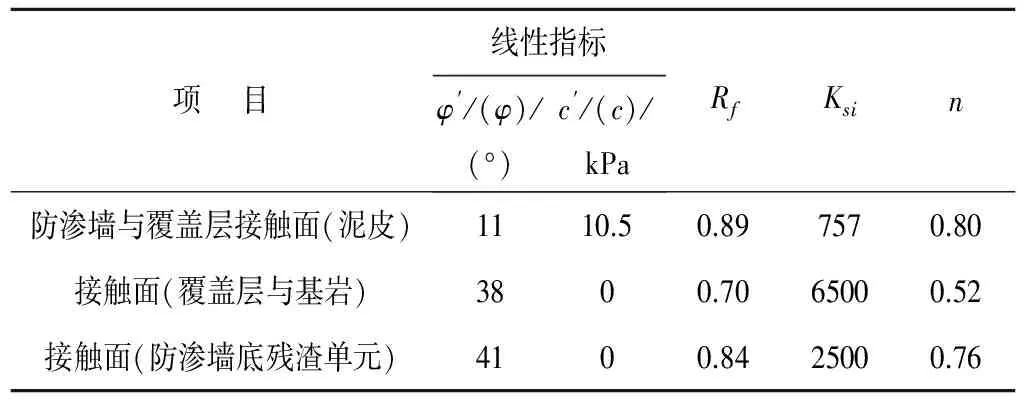
表2 接触面参数Tab.2 Material parameters of contact elements

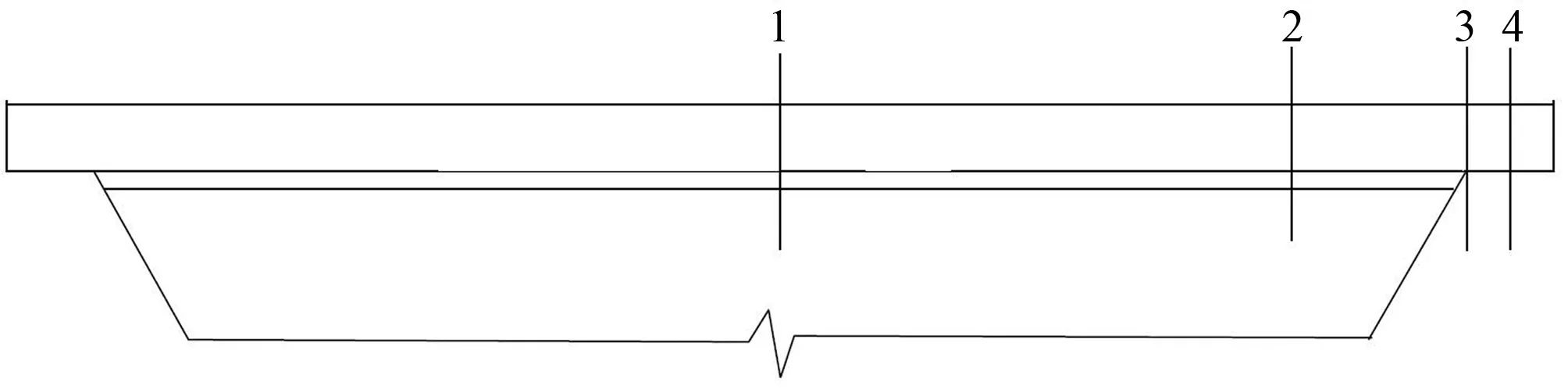
图2 典型剖面示意图Fig.2 positions of typical gallery profile 注：1剖面为廊道中央剖面，2剖面为廊道河床段剖面，也即约廊道靠右岸1/6跨剖面，3剖面为廊道右岸岩台边缘剖面，4剖面为廊道右岸岩台中央剖面。

3.1 典型坝型坝基廊道应力变形规律分析

坝基廊道整体变形图如图3所示，典型剖面应力图如图4所示，其中图4(a)～图4(b)表示廊道中央剖面，图4(d)～图4(f)表示廊道靠近右岸1/6跨的剖面。

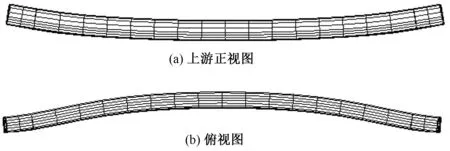
图3 廊道变形图(变形放大50倍)Fig.3 deformation diagram of gallery(Magnified 50 times)

廊道在上游水荷载、自重以及上覆土压力的作用下向下游发生挠曲，同时竖直向下挠曲，整体变形从两岸到河床中央逐渐增大，最大值出现在河床中央，左右两边变形基本对称。

廊道中央剖面横河向基本全面受压，上游侧压应力相比下游侧压应力偏大，压应力极值出现在上游侧外边墙顶部。在顺河向，廊道顶拱和底板出现受拉区，拉应力极值发生在底板内侧，压应力极值发生在顶拱外侧。竖直向呈受压状态，压应力极值出现在下游侧内边墙中部。

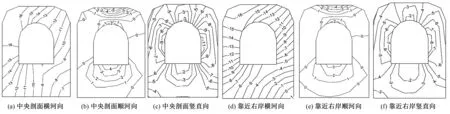
图4 典型剖面正应力(左侧为上游侧 单位：MPa)Fig.4 stresses of typical gallery profiles(upstream on the left)

在河床段剖面，横河向基本受压，压应力极值位于廊道顶拱外侧靠近上游的部位，只在下游侧外边墙底部，出现小范围拉应力，这是廊道发生挠曲时下游侧土的反力造成的。顺河向正应力和竖直向正应力分布规律与中央剖面应力分布规律基本一致，但应力极值有所减小。廊道在两岸岩台边缘处发生弯曲，故此处横河向正应力在上游侧发生拉应力集中而在下游侧发生压应力集中。

3.2 覆盖层厚度对坝基廊道应力变形影响

由于覆盖层结构松散，压缩性大，对坝基廊道应力变形的影响不容忽视，根据已建坝基防渗采用廊道—防渗墙型式高土石坝的覆盖层厚度统计[5,6]，本文选取覆盖层厚度分别为40、60、80、100 m的4种方案进行分析，示意图如图5所示。

坝基廊道应力变形随覆盖层厚度变化曲线如图6所示。

影响规律分析如下。

(1)覆盖层为100 m时的廊道顺河向位移极值为21.67 cm，相比覆盖层为40 m时16.24 cm增加33.4%；竖直向沉降极值为-14.33 cm，与覆盖层为40 m时-9.48 cm相比增加51.2%；横河向向左、右岸水平位移分别增加53.9%、54.3%。各方向位移增长幅度较大，但增速随覆盖层厚度增加逐渐趋于平缓。

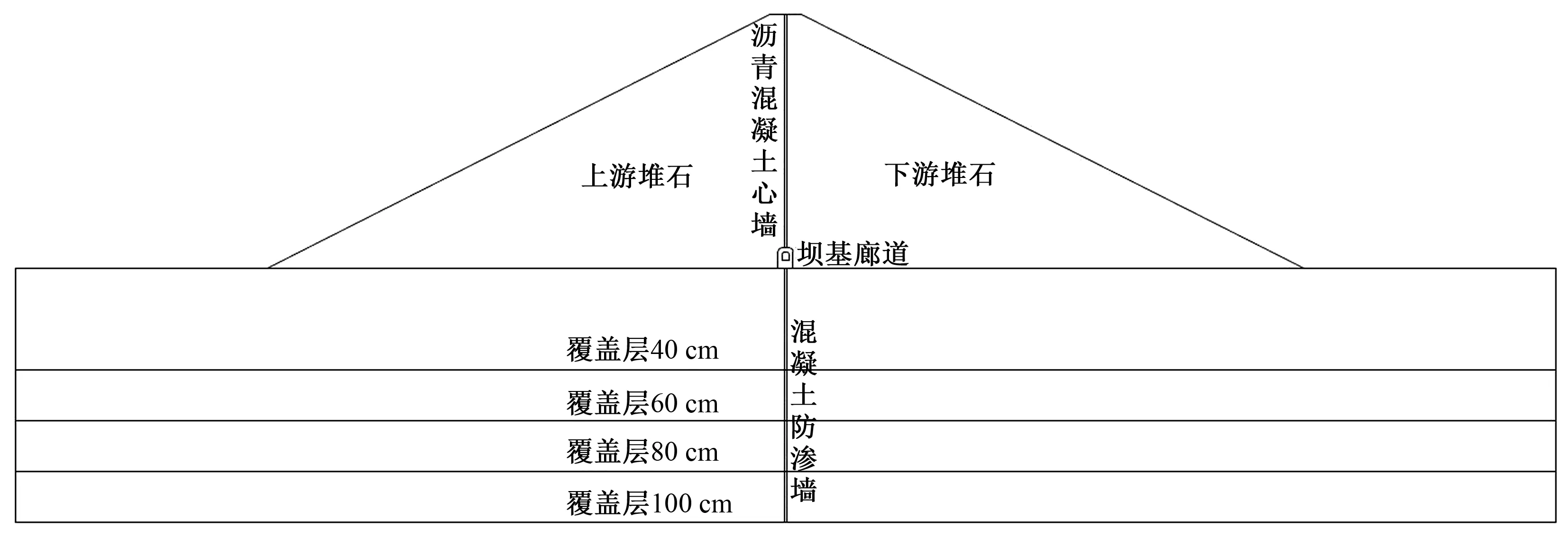
图5 不同覆盖层厚度横剖面示意简图Fig.5 Sketch map of cross section corresponding to different overburden thickness

图6 廊道位移和应力极值随覆盖层厚度变化曲线Fig.6 Variation curves of gallery displacement and stress extreme value with overburden depth

这主要是由于覆盖层属于柔性材料，压缩性较大，覆盖层越厚，基础越软弱，廊道竖直向沉降就越大。防渗墙也随覆盖层的加厚而加深，受到的上游水压力也越大，故顺河向变形增大。在覆盖层向下加厚的过程中，覆盖层增加的部分离廊道越来越远，故覆盖层厚度的增加对廊道沉降变形的影响越来越小，且增加部分河谷越来越窄，对防渗墙约束作用越来越大，而廊道与防渗墙之间刚性连接，导致变形最大值增长变缓。

(2)覆盖层从40 m逐渐加厚至100 m时，廊道中央剖面各个方向应力分布规律基本不变，只是应力值有所增大，横河向压应力极值增长了74.4%，增长速度逐渐变慢，而顺河向与竖直向正应力增长幅度均比较小。因此，覆盖层厚度的变化对廊道中央剖面顺河向和竖直向正应力的影响不大，但对横河向正应力影响较大。

这是由于随着覆盖层加厚，廊道中间段受力增大，顺河向及竖直向挠曲增大，导致中央剖面应力极值增大。随着覆盖层加厚，覆盖层增加部分距离廊道越来越远，故对其影响越来越小；且增加部分河谷形状逐渐变窄，基岩对防渗墙的约束作用逐渐加强，防渗墙的变形受到一定限制，从而与防渗墙刚性连接的廊道，挠曲变形的增大速度也减缓，故中央剖面应力极值的增长逐渐变慢。

(3)对于廊道靠右岸1/6跨剖面，在覆盖层从40 m逐渐加厚至100 m过程中，横河向应力变化较大，下游侧外边墙底部应力由2.06 MPa的拉应力变为-0.31 MPa的压应力，减小了115.0%，顶拱外侧的横河向压应力极值增大了41.7%；顺河向和竖直向应力增长幅度均比较小。由此知，廊道河床段剖面顺河向和竖直向正应力对覆盖层厚度的变化不敏感，但该剖面横河向正应力受覆盖层厚度影响较大。随着覆盖层加厚，横河向正压应力极值有一定增大，而廊道河床段下游侧反弯段拉应力区域逐渐减小。这是由于覆盖层越厚，上游水压力也越大，廊道凸向下游发生的弯曲程度越大，下游侧土的反力随之增大，但土的反力增加程度没有向下游作用力增加程度大，故河床段下游侧受拉区域逐渐减小。

3.3 河谷宽度对坝基廊道应力变形的影响

由于廊道的跨度随河谷宽度变化而变化，故河谷宽度会对坝基廊道，尤其是河床段的应力变形产生较大影响。本文选取了以下5种方案进行分析：河谷宽度分别为80、150、200、250、300 m(图7)。

计算结果如图8～图9所示。计算结果分析如下。

(1)河谷宽为300 m时的顺河向位移为26.67 cm，极值相比河谷宽为80 m时10.18 cm增加了162.0%，竖直向沉降为15cm，相比于河谷宽为80 m时6.33 cm增加了137.0%，横河向向左、右岸水平位移分别增加了124.5%、124.9%。从整体上看，河谷宽度增加过程中各方向位移极值有了明显增长，尤其是顺河向水平位移，增长幅度最大。这是由于河谷宽度增大后，受到更大的上覆土压力、自重及水压力作用，导致廊道变形增大。同时，随着河谷宽度不断增大，廊道各方向位移极值增长速度在渐渐变缓。这是由于河床段越长，廊道中间部分的变形分布越均匀，越来越趋近于一条直线，极值的增长也就越来越慢。

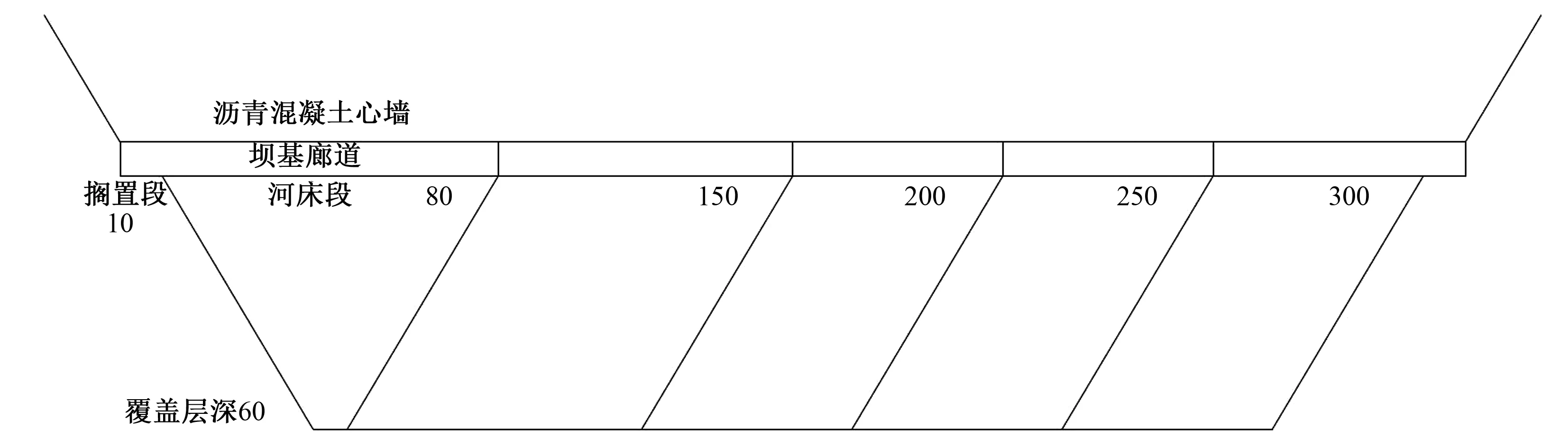
图7 不同河谷宽度纵剖面简图(单位：m)Fig.7 Schematic diagram of longitudinal profile of different Valley width

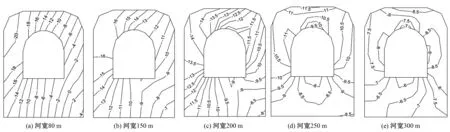
图8 廊道中央剖面横河向正应力 (左侧为上游侧 单位：MPa)Fig.8 longitudinal tensile stress diagram of central section of gallery

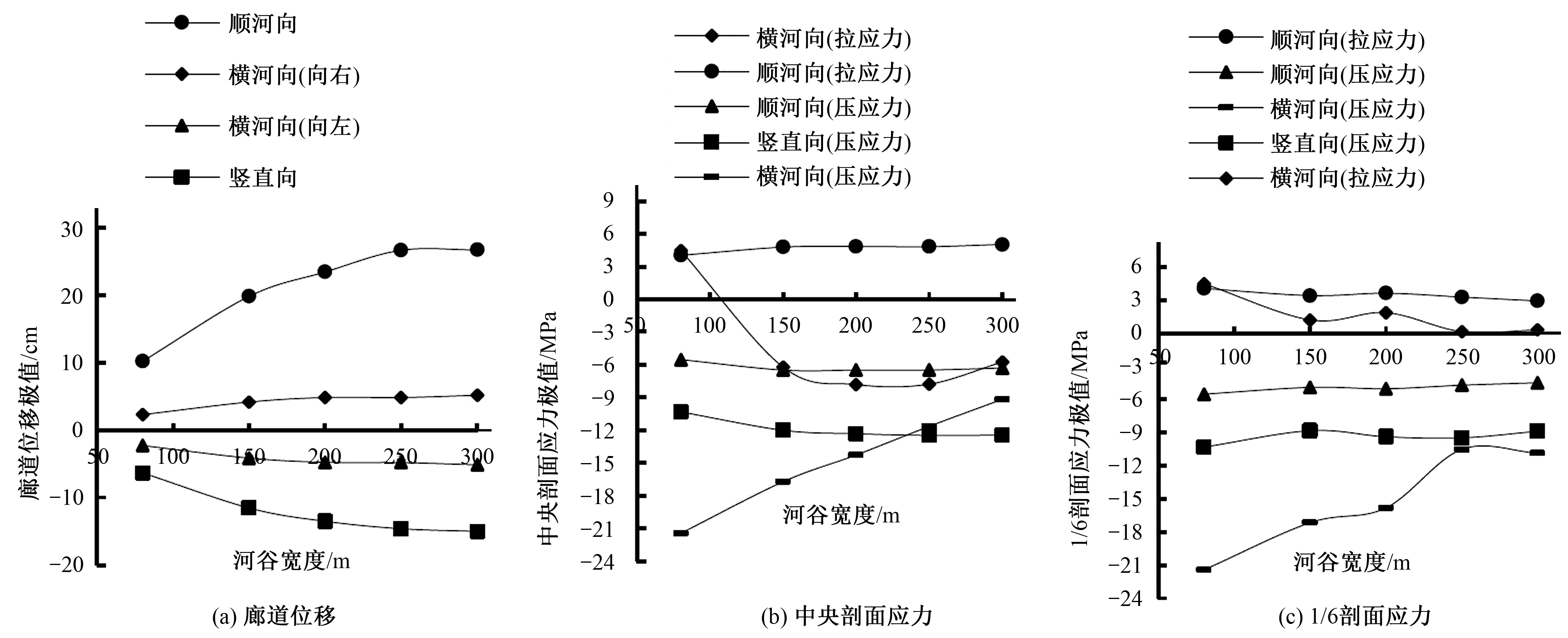
图9 廊道位移和应力极值随河谷宽度变化曲线Fig.9 Variation curves of gallery displacement and stress extremum with valley width

(2)河谷宽度不同时，廊道中央剖面顺河向及竖直向正应力分布规律基本不变，极值增长幅度较小。横河向正应力分布规律发生变化，河谷宽度为80 m时，中央剖面横河向压应力值从上游侧到下游侧越来越小，最大值出现在上游侧外边墙顶部，为-21.43 MPa，在下游侧外边墙底部出现小面积受拉区，拉应力极值为4.49 MPa。随着河谷宽度的增大，中央剖面横河向压应力极值逐渐减小，横河向受拉区也逐渐消失，在河谷宽度达到150 m及以上的方案中，横河向正应力全部为压应力。河谷宽度达到250 m时，横河向压应力最大值出现在廊道顶拱外侧略靠上游处，最小值出现在廊道底板内侧中央部位；河谷宽度达到300 m时，横河向压应力最大值为-9.15 MPa，位于下游侧内边墙中部，最小值为-5.73 MPa，位于廊道底板内侧略靠上游处。

(3)在河谷宽仅为80 m时，廊道河床段并没有出现反弯段，河床段横河向拉应力极值出现在中央剖面，距右岸岩台40 m。在河谷宽大于150 m时，河床段均在靠近岩台处出现反弯段，产生小范围的拉应力集中区。河谷宽度为150 m时，廊道河床段横河向拉应力极值位于距右岸岩台约1/6跨剖面；河谷宽为200 m时，横河向拉应力极值位于距右岸岩台约1/7跨剖面；河谷宽为250 m时，横河向拉应力极值位于距右岸岩台约1/8跨剖面；河谷宽为300 m时，横河向拉应力极值位于距右岸岩台约1/9跨剖面。

河谷宽度从80 m增加到300 m过程中，河床段剖面各方向正应力分布规律变化不大，极值均有所减小，廊道河床段横河向拉应力极值位置从距右岸约1/6跨剖面向右岸横移，拉应力值变化较大，减小了93.3%，横河向压应力极值变化幅度稍小，减小了49.4%；顺河向拉应力、压应力以及竖直向压应力极值变化幅度均比较小。由此知，廊道河床段顺河向和竖直向正应力对河谷宽度的变化不敏感，但该剖面横河向应力受河谷宽度影响较大。

3.4 两岸搁置段长度对坝基廊道应力变形的影响

廊道两岸岩台搁置段长度不同时，两岸约束作用也随之改变，从而对廊道，尤其是两岸岩台边缘附近的应力变形规律，产生一定影响，本文选取两岸搁置段长度分别为2、5、10、15、20 m 5种方案进行分析(图10)。

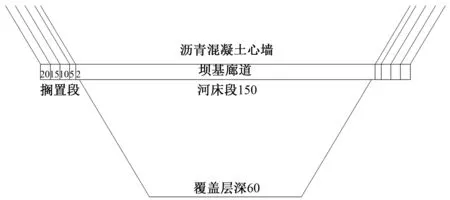
图10 不同搁置段长度纵剖面简图(单位：m)Fig.10 Schematic diagram of longitudinal section with different length

计算结果如图11所示。计算结果分析如下。

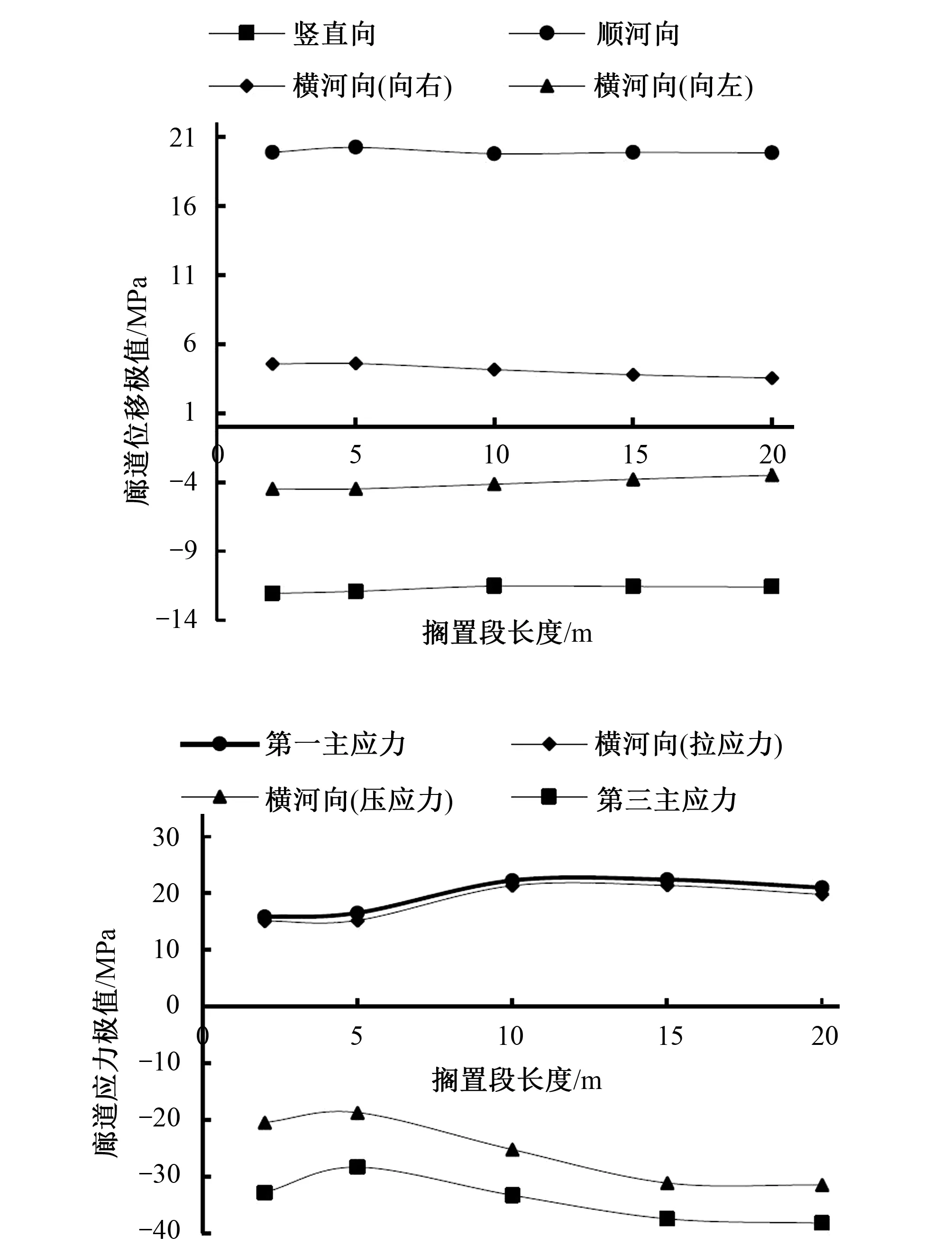
图11 廊道位移和应力极值随搁置段长度变化曲线Fig.11 Variation curves of gallery displacement and stress extremum with different length

(1)随着搁置段长度不断增大，各方向的位移极值整体稍有减小，但变化并不明显。搁置段长为20 m时的顺河向位移极值相比搁置段为2 m时，减小了0.2%；搁置段长为20 m时的竖直向沉降，相比于搁置段为2 m时，减小了3.9%，横河向向左岸、右岸水平位移分别减小了22.0%、22.4%。这是由于两岸搁置段越长，则岩台越长，两岸基岩的约束作用越大，从而各方向的位移受到一定限制而略有减小。从整体上看，两岸搁置段长度从2 m增加到20 m过程中，各方向位移极值变化幅度很小，尤其是顺河向和竖直向位移极值，基本保持不变。故廊道两岸搁置段长度的变化对廊道整体的变形影响不大。

(2)随着搁置段增长，横河向拉应力及第一主应力出现的位置不变，均在右岸岩台边缘剖面的上游侧底部，应力极值先急剧增大，然后略有减小。搁置段为15 m时的横河向拉应力及第一主应力极值达到最大值，相比搁置段为2 m时应力极值增长幅度最大，分别增长了41.6%和41.5%，搁置段增加到20 m长时，应力极值稍有降低。横河向压应力和第三主应力均出现在右岸岩台边缘剖面的下游侧底部，搁置段为20 m时的应力极值，相比搁置段为2 m时应力极值增长幅度最大，分别增长了53.9%和16.5%。由此可知，廊道两岸搁置段长度的变化对廊道整体横河向拉应力、压应力及第一主应力拉应力极值均有较大的影响。这是由于当岩台搁置段长度增长时，两岸基岩的约束作用增大，搁置段受力变大。

4 结 语

本文重点探讨了覆盖层厚度、河谷宽度以及两岸岩台搁置段长度对坝基廊道应力变形的影响，对比分析，主要结论如下：

(1)随着覆盖层厚度的不断增大，廊道应力变形分布规律、极值出现位置基本不变，但极值变化较大。廊道整体各方向变形极值均不断增大，但增长速率逐渐减小。对于廊道中央剖面，各方向正应力极值不断增长，但增长速率逐渐变小。对于廊道靠右岸1/6跨剖面，横河向正应力拉应力极值减小较大，压应力极值增大，顺河向及竖直向正应力的极值基本不变。工程建设中应根据覆盖层的具体厚度，对廊道配筋进行适当调整，尤其应注重1/6跨廊道下游侧底部纵筋配置。

(2)河谷宽度的增大对廊道应力变形影响较大。廊道各方向位移极值不断增大，但增长速度趋于变缓，廊道中央附近的变形越来越接近一条直线。对于廊道中央剖面，横河向正应力在剖面上的分布越来越均匀，应力值减小 较大，其中拉应力变成了压应力。顺河向及竖直向正应力分布规律基本不变，应力极值增长幅度也较小。对于廊道河床段横河向拉应力极值剖面，虽然在不同河谷宽度时，此剖面出现的位置有所不同，但均出现在距离岩台约25～40m处。

(3)两岸搁置段的长度增大对整体应力影响较大，而对廊道整体变形影响较小。搁置段越长，两岸岩台约束作用越强，岩台边缘处的弯曲变形越明显。在设计和施工中应尽量避免把廊道过长地放置在两岸岩台上。

□

参考文献：

[1] 段亚辉. 高等坝工学[M]. 北京 : 中国水利水电出版社, 2013.

[2] 孙 陶. 邓肯-张非线性弹性模型的研究现状[J]. 水电站设计，2006,(3).

[3] 殷宗泽, 许国华. 土与结构材料接触面的变形及其数学模拟[J]. 岩土工程学报, 1994,16(3):14-22.

[4] 万 彪, 何蕴龙, 熊 堃. 有厚度节理单元的开发与应用[J]. 水电能源科学, 2008,26(4): 63-66.

[5] 熊 堃, 何蕴龙, 伍小玉, 等.长河坝坝基廊道应力变形特性研究[J]. 岩土工程学报, 2011,33(11):1 767-1 774.

[6] 曹学兴. 深厚覆盖层地基高土质心墙堆石坝抗震安全性研究[D]. 武汉：武汉大学，2013.

[7] 游宇豪. 深厚覆盖层上高土石坝坝基防渗系统合理计算方法研究、验证与应用[D]. 武汉：武汉大学, 2015.

[8] 何蕴龙,苗 君,游宇豪,等.土石坝心墙与防渗墙廊道连接结构应力变形分析[R]. 武汉大学水利水电学院，2015.

[9] 冯 蕊, 伍小玉,何蕴龙,等. 深厚覆盖层上超高心墙堆石坝坝基廊道非线性开裂分析[J]. 四川大学学报: 工程科学版, 2015,47(1): 60-67.

[10] 冯 蕊, 何蕴龙, 白新革. 高心墙堆石坝坝基廊道受力特性研究[J]. 岩土工程学报,2017,39(7):1 241-1 250.