反舰导弹的超前动态抗饱和控制器设计与仿真∗

潘长鹏 赵红超 王 亭

（海军航空大学 烟台 264001）

1 引言

控制系统的Windup现象，是由于被控对象的输入受限，使得被控对象的实际输入与控制器的输出不相等，引起闭环系统响应变差（如超调变大、调节时间变长、甚至系统失去稳定性）的现象。为了克服Windup现象，保证控制系统的良好品质，需要在控制器设计中加入抗饱和（Anti-Windup）设计算法［1］。国内外研究者针对工业控制系统的输入受限问题已进行了大量研究，提出了许多不同形式的抗饱和控制器设计算法［2～7］。

反舰导弹的过载控制系统中同样存在Windup现象，由于能量有限或者机械强度限制，执行机构的工作存在饱和约束［8～9］。当执行机构工作达到饱和值时将会导致有效控制力矩显著不足，进而引起导弹控制系统品质下降甚至不稳定。前期我们对导弹控制系统抗饱和设计方案进行了初步研究，通过仿真分析发现，当采用静态抗饱和算法时，虽然能够减小系统输入量的大小，但是减小以后的值仍然超过饱和值，执行机构并没有脱离饱和工作状态。当采用动态抗饱和算法时能够在一定程度上将系统输入量减小到饱和值以下，使执行机构饱和工作状态时间减小52%以上。那么，有没有更好的抗饱和算法能够使执行机构完全脱离饱和工作状态呢？

文献［10～11］对抗饱和机构的三种激活方式进行了详细研究，即立即激活方式、超前激活方式和滞后激活方式。通过仿真结果比较，证明了超前激活方式的抗饱和性能优于立即激活方式和滞后激活方式，而且，超前激活方式还能够扩大系统原点的吸引域。借鉴上述研究成果，本文将前期设计的动态抗饱和算法改进为超前激活方式（简称为超前动态抗饱和算法），进一步研究反舰导弹过载控制系统中的超前动态抗饱和控制器设计方案，以实现导弹执行机构完全脱离饱和工作状态的目标。

2 反舰导弹运动模型

超声速反舰导弹具有轴对称气动外形，其俯仰通道和偏航通道的结构是基本一致的；滚动通道仅起稳定作用，维持滚动角为零。俯仰通道和偏航通道采用过载控制系统，下面以俯仰通道为例进行研究。反舰导弹采用了冲压发动机，其正常工作要求反舰导弹的攻角和侧滑角都为小角度，在小角度条件下可以进行线性化处理，从而建立反舰导弹俯仰通道的运动模型如下：

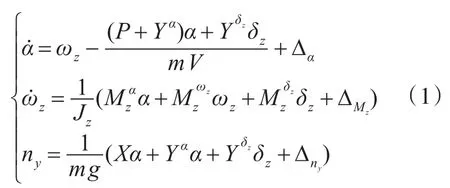
式中：为建模误差，都是有界量；弹体过载ny为系统输出量；其它各个变量的物理意义参见《导弹飞行力学》［12］。

将作为执行机构的舵机系统视为一阶惯性环节，即

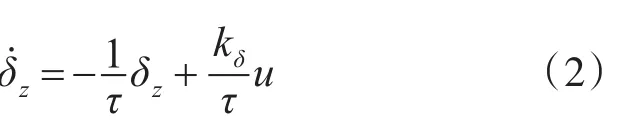
式中：τ为舵机系统的时间常数；kδ为放大系数；u为系统输入量，即送入舵机的电压信号。实际上，u是受到饱和限制的。

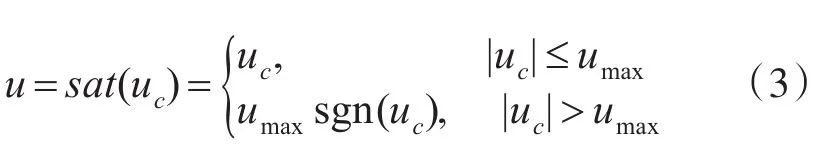
式中：uc是控制器的输出，即控制算法解算得出的值；umax为送入舵机的电压最大值。uc经过饱和环节后成为实际的系统输入u。为了便于分析，在运动模型建立时先不考虑饱和环节。

将式（1）的第3个方程代入第1个方程，整理可得

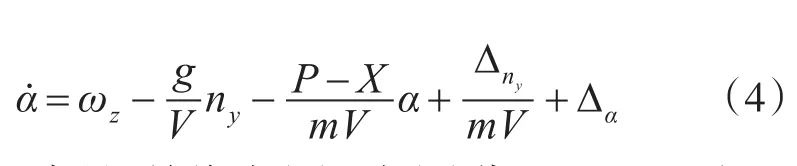
对ny求导，并将式（2）、式（4）代入，整理可得

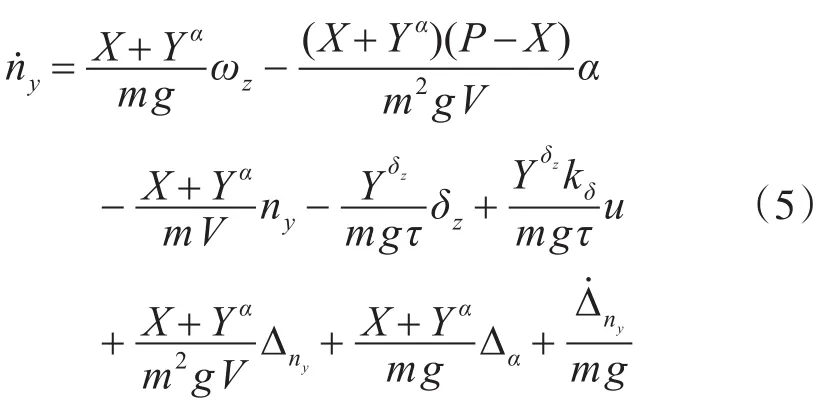
利用容易测量的导弹状态量过载ny和角速度ωz来设计控制系统，以ny和ωz的线性组合构造组合状态量ξm，并将其作为系统的新输出量［8～9］

对ξm求导，并将式（5）和式（1）的第2个方程代入，整理可得

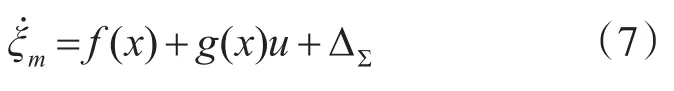
式中：

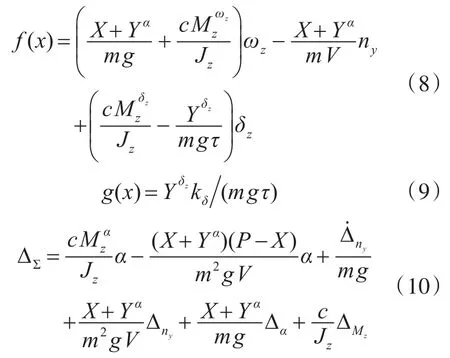
f(x)和g(x)为已知量；ΔΣ称为“汇总不确定项”，由于α是不可测的未知量，因此含有α的项也是不确定项。

3 扩展状态观测器设计

针对汇总不确定项，采用扩张状态观测器来设计估计器。将汇总不确定项ΔΣ看作是未知的被扩张的状态变量：ξm2=ΔΣ，并设其中：ζ(t)是未知函数，由此式（7）变换为

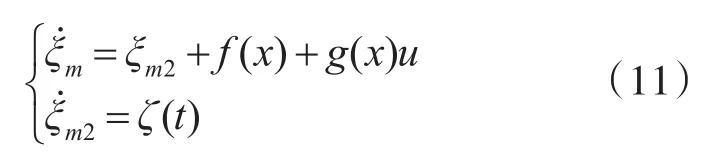
扩张状态观测器设计为［13］

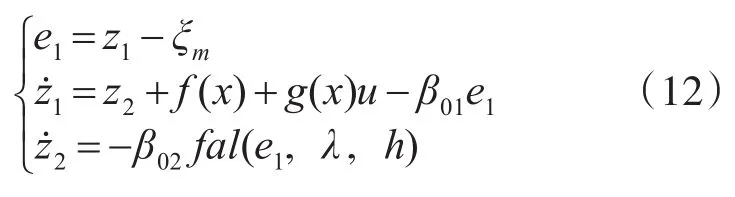
式中：β01＞0，β02＞0，0＜λ＜1，0＜h＜1；fal函数的表达式为

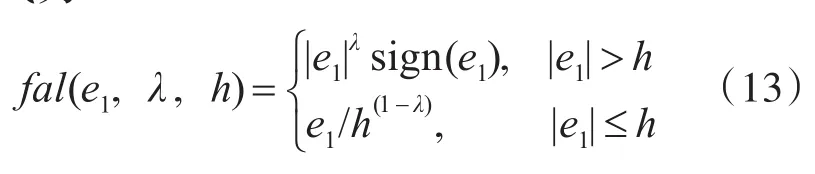
设e2=z2-ξm2，由文献［13］的研究可知，当系统进入稳态时，估计误差满足：

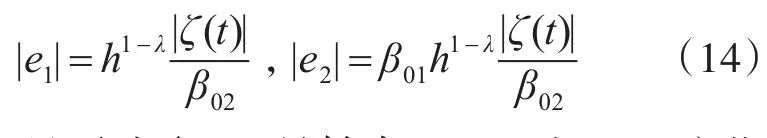
因此，只要选取β02足够大于ζ(t)和β01，这些估计误差都会很小；从而扩张状态观测器中的状态z2能够很好地估计汇总不确定项ΔΣ。因此，在下面的控制器设计中将以z2代替式（7）中的ΔΣ。

4 控制器设计

控制器设计采用国内外研究者们常用的二步法设计方法，即首先不考虑执行机构的饱和限制，设计出满足系统性能指标的标准控制器；然后加入超前动态抗饱和补偿算法，克服非线性饱和因素引起的不良影响，起到抗饱和的作用。

4.1 标准控制器设计

首先不考虑执行机构的饱和限制，认为u=uc。考虑到滑模控制方法对参数摄动和外界干扰等具有强鲁棒性，下面采用滑模控制方法来设计标准控制器。设ny，ωz，ξm的指令信号分别为nyc，ωzc，ξmc；则

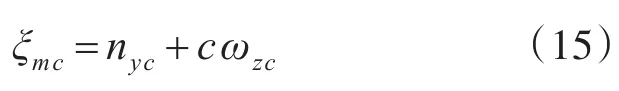
ξm的跟踪误差定义为

考虑到系统（7）的相对度为1，选取滑模面为

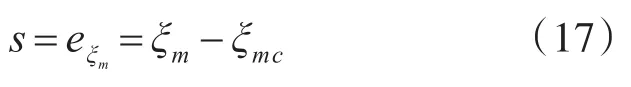
显然，当系统状态轨迹到达滑模面时跟踪误差也就收敛到零了。对式（17）求导，并将式（7）代入可得

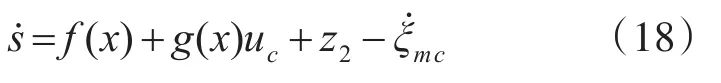
为了使系统状态轨迹在有限时间内到达滑模面，并且在到达过程中具有良好的动态品质，采用如下的指数趋近律：

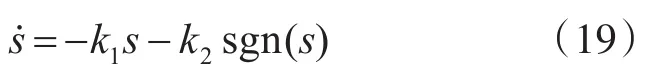
式中：k1＞0，k2＞0，sgn(s)为符号函数。

联立式（18）和式（19）可以解得

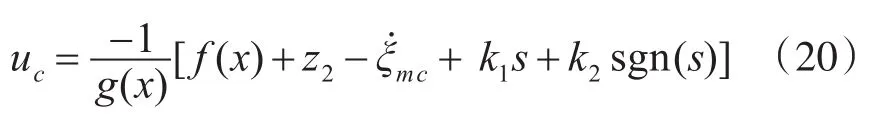
在实际应用中，为了削弱滑模控制的抖振现象，通常对符号函数sgn(s)进行连续化处理，以连续函数替代sgn(s)，其中：ε为一小正数。

4.2 超前动态抗饱和控制器设计

前面设计标准控制器时没有考虑饱和环节，实际的控制输入量送入舵机时是受到饱和限制的，由式（3）表示。采用超前动态抗饱和算法来抑制饱和环节的影响，超前激活方式是在原来的饱和环节前面引入一个人为设置的饱和环节，其饱和度低于执行机构的饱和度，以此饱和环节为基础设计抗饱和补偿器。因此，在系统控制输入达到饱和值之前该抗饱和补偿器已经被激活，从而产生抗饱和作用。将超前动态抗饱和补偿器加入到标准控制器中，从而构建了超前动态抗饱和控制器。

人为设置的饱和环节的输出ua为

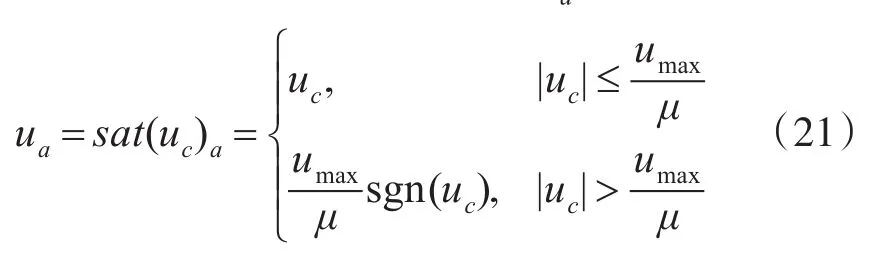
式中：μ＞1；即，人为设置的饱和环节的饱和度小于umax。

超前动态抗饱和补偿器设计为

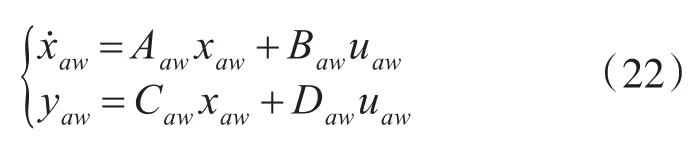
式中：Aaw、Baw、Caw和Daw为抗饱和参数，它们都是常数；uaw为输入量；yaw为输出量。

将yaw加入到原来的滑模控制器中，从而构建超前动态抗饱和控制器如下：

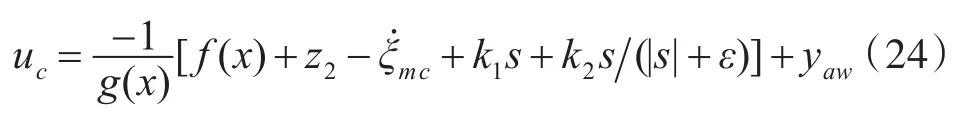
5 仿真分析

超声速反舰导弹在高空飞行时气动控制效率很低，当过载指令信号突变或者导弹做大机动转弯时，需要执行机构提供很大的驱动力矩才能完成控制任务。由于存在饱和限制，反舰导弹的实际控制输入不够大，与控制器的输出不一致，进而引起Windup现象。

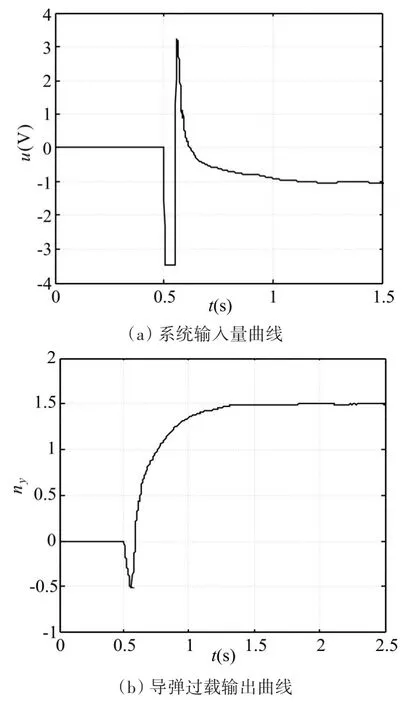
图1 在特征点1处不加入抗饱和补偿器的仿真结果

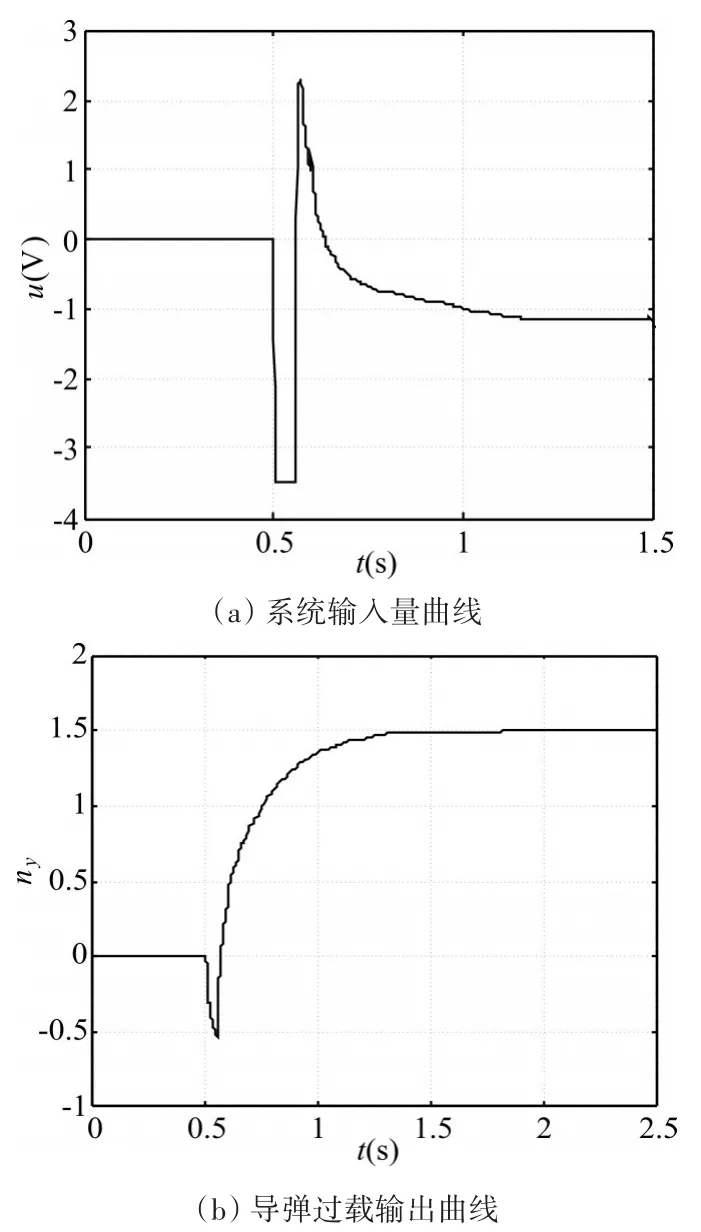
图2 在特征点2处不加入抗饱和补偿器的仿真结果

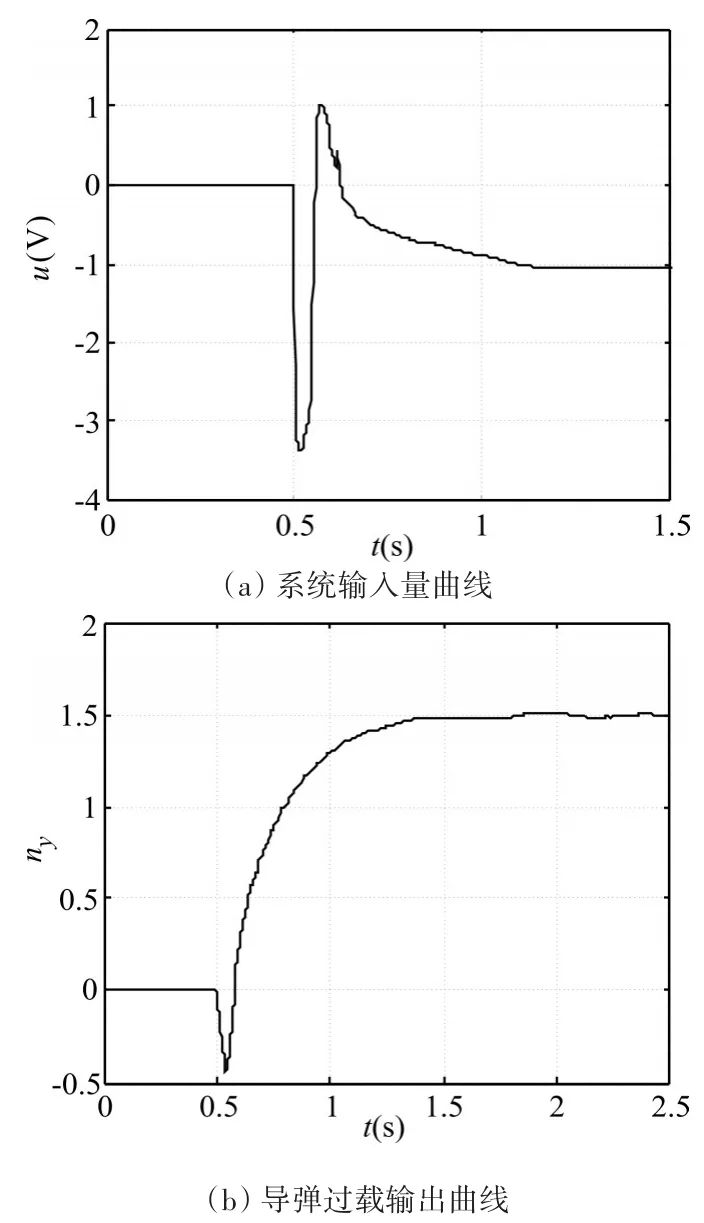
图3 在特征点1处加入抗饱和补偿器的仿真结果

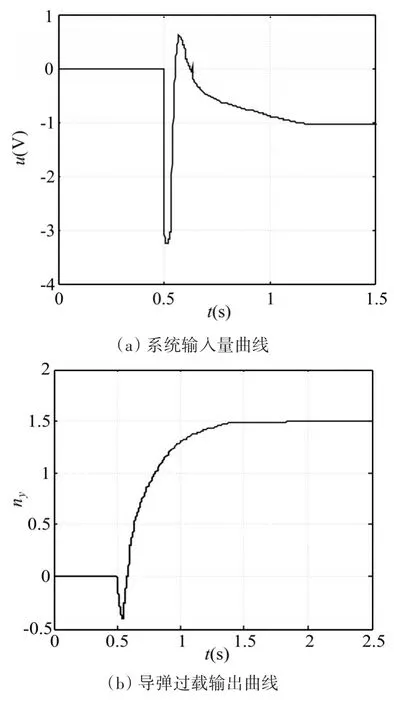
图4 在特征点2处加入抗饱和补偿器的仿真结果

从反舰导弹飞行高度大于14500m的高空弹道上选取2个特征点（编号为1、2）进行仿真分析，并且对不加入和加入超前动态抗饱和补偿器两种情况进行仿真对比。不加入抗饱和补偿器时控制器为式（20），加入抗饱和补偿器时控制器为式（24）。仿真中，反舰导弹俯仰通道运动模型（1）中的建模误差假设为周期为0.6s的正弦函数，其幅值（以A( ⋅ ) 表 示 ） 分 别 为 ：舵机系统的参数为：τ=0.05s，kδ=0.12，送入舵机的电压最大值为：uδmax=3.5V。选取0.5s启动的幅值为1.5的阶跃信号表示过载指令信号发生了突变。通过仿真调试，确定扩张状态观测器的参数为：β01=170，β02=1800，λ=0.5，h=0.04；超前动态抗饱和控制器的参数为：μ=1.2，Aaw=-10，Baw=50，Caw=75，Daw=2.0，k1=30，k2=2.15，c=-78，ε=0.05。不加入抗饱和补偿器时，2个特征点处的仿真结果分别如图1、2所示。加入超前动态抗饱和补偿器时，2个特征点处的仿真结果分别如图3、4所示。

由图1～图4的仿真结果对比可知，对于2个特征点而言，在不加入抗饱和补偿器时，导弹系统的执行机构都有一段时间处于饱和工作状态；而加入超前动态抗饱和补偿器后，执行机构完全脱离了饱和工作状态，导弹的过载输出曲线也基本没有变化。因此，超前动态抗饱和控制器显著地减轻了执行机构的工作强度，提高了反舰导弹过载控制系统的控制性能。

6 结语

本文对超声速反舰导弹的过载控制系统进行了研究。以导弹过载和角速度的线性组合构造组合状态量，建立了导弹俯仰通道的运动模型。为了对系统中的汇总不确定项进行有效估计，采用扩张状态观测器设计了估计器。针对执行机构饱和问题，提出了将超前动态抗饱和算法加入到控制器设计中，即在标准控制器设计的基础上，加入超前动态抗饱和补偿器，综合起来构成了超前动态抗饱和控制器。从反舰导弹高空弹道上选取2个特征点进行了仿真分析，仿真结果表明，不加入抗饱和补偿器时执行机构存在饱和工作状态；而加入抗饱和补偿器时执行机构完全脱离了饱和工作状态，提高了反舰导弹过载控制系统的控制性能。

参考文献

［1］Tarbouriech S，Turner M.Anti-windup design：an over⁃view of some recent advances and open problems［J］.IET Control Theory and Application，2009，3（1）：1-19.

［2］Yang Ming，Niu Li，Xu Dian-Guo.A novel piecewise an⁃ti-windup design for speed loop PI controller of PMSM ser⁃vo system［C］//The 14th International Power Electronics and Motion Control Conference，2012：1-4.

［3］李钟慎，牛彬.一种采用条件技术的抗饱和补偿控制器［J］. 华侨大学学报（自然科学版），2011，32（1）：10-12.

［4］Galeani S，Onori S，Teel A R，et al.A magnitude and rate saturation model and its use in the solution of static an⁃ti-windup problem［J］.Systems&Control Letters，2008，47：1-9.

［5］Song Xiaona，Fu Zhumu，and Liu Leipo.Robust stabiliza⁃tion of state delayed discrete-time Takagi-Sugeno fuzzy systems with input saturation via an anti-windup fuzzy de⁃sign［J］.Chinese Physics-B，2012，21（11）：118701：1-118701：8.

［6］Zhao Junjie，Wang Jing，Shen Hao.Dynamic anti-wind⁃up control design for Markovian jump delayed systems with input saturation［J］.Circuits System Signal Process，2013，32：2213-2229.

［7］ Li Yuanlong，Lin Zongli.Design of saturation-based switching anti-windup gains for the enlargement of the do⁃main of attraction［J］.IEEE Transactions on Automatic Control，2013，48（7）：1810-1816.

［8］赵红超，高晓冬，范绍里.基于抗饱和补偿的导弹过载控制系统设计［J］. 南京理工大学学报，2012，36（增刊）：154-159

［9］Xianjun Shi，Hongchao Zhao，KewenXu.Dynamic An⁃ti-windup Design for Missile Overload Control System［J］.Applied Mechanics and Materials， 2012： 236-237，273-277.

［10］Wu Xiongjun，Lin Zongli.Design of multiple anti-wind⁃up loops for multiple activations［J］.Science China-In⁃formation Sciences，2012，44（9）：1924-1934.

［11］Wu Xiongjun，Lin Zongli.Dynamic anti-windup design for anticipatory activation：enlargement of the domain of attraction［J］. Science China-Information Sciences，2014，47，012201：1-012201：14.

［12］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学出版社，2012：5-18.

［13］Han Jingqing.From PID to active disturbance rejection control［J］.IEEE Transactions on Industrial Electron⁃ics，2009，56（3）：900-906.