发动机下发时间预测和机队下发方案优化

赵洪利，陈民恺，刘诗雄

（中国民航大学a.航空工程学院；b.中欧航空工程师学院，天津 300300）

为了对发动机机队的拆换计划进行合理规划，首先需要对机队中各台发动机的下发时间进行预测。发动机排气温度裕度（EGTM，exhaust gas temperature margin）是表征发动机性能状态的重要参数[1]。随着发动机使用时间的增加，EGTM会逐渐下降，当其下降到某个阈值时，发动机应下发送修。发动机性能衰退预测主要使用多参数模型，如基于Weibull比例风险回归的建模思想[2]，基于卡尔曼滤波算法的时变参数退化量模型[3]；而单参数EGTM模型包括基于分段线性拟合[4]和基于时间序列方法的预测模型[5]。

发动机拆下送修时，为使飞机不停飞，必须在机队可用备发中为该飞机选择更换的发动机。一般情况下，机队中各台备发的型号、性能、剩余寿命、部件损伤情况不同，如何选择要安装的发动机是机队下发方案优化的内容；若无备发，会出现缺发情况，导致以下后果：①飞机停飞，造成经济损失；②购买新发，增加备发数量，增加成本；③租用发动机[6]。选择不同的备发，将影响机队未来运营时的缺发情况。因此，合理规划机队调度计划，可降低整个机队的缺发时间，从而减少航空公司的运营成本，提高经济效益。目前这方面研究主要采用基于排序原则的方法[7]，另外，文献[8]使用启发式算法，研究了拆发计划方案集的构造方法和选择方法。

1 发动机下发时间预测

对机队中各台发动机的下发时间进行预测，是合理制定机队下发方案的前提。导致发动机下发的原因主要有性能衰退、时寿件到寿、部件损伤达到或超过限制值和适航指令/服务通告限制，而具体某台发动机的下发时间应为以上影响因素中最先到达者。研究主要从性能衰退的角度，对下发时间进行预测。

航空公司通常使用发动机机队的年平均EGTM千次循环衰退率来估计发动机到达EGTM裕度警戒值时的循环数。由于个体发动机往往不服从群体的平均模型，故上述方法的预测精度并不高。而把机队各台发动机看成相互独立的个体进行预测，信息量过少，且忽略了个体与个体之间可能存在的联系。综合考虑以上因素，认为机队中各台发动机的性能衰退并不完全相同，但可能存在几种相似的衰退规律，因此，采用数据聚类分析方法中的经典K-means算法对下发期限进行预测。

算法主要流程如下：

1）确定分类个数K；

2）针对N个样本，选择K个作为初始聚类中心（Z1，…，Zk）；

3）对每个样本Xi找到离其最近的聚类中心Zi，并将其分配到Zi所标记的类Ui中；

4）采用算术平均的方法计算聚类中心；

5）返回步骤2），直到分类不再变化；

6）最后根据所需预测样本的历史数据，以距离最小为原则，将该样本分至其中一类中，并认为该类聚类中心的发展趋势就是该样本的未来发展趋势。

K-means算法存在以下局限性：

1）结果受初值影响。采用多次随机生成初值，挑选类内距离最小的结果。

2）需要人为确定分类个数，并且无法对分类方案的优劣进行评价。针对这一问题，在现有研究基础上[8-10]提出了准则函数P，用于评价分类个数，即

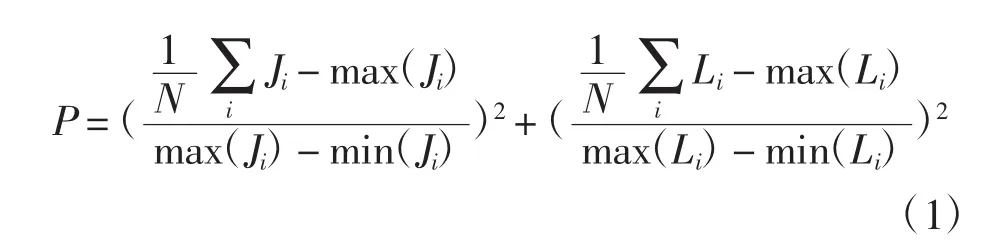
其中：N为元素总数；Li为元素i的类内平均距离；Ji为元素i的最小类间距离。类内距离越小越好，说明类紧凑；类间最小间距越大越好，说明类与类之间差别明显。基于以上条件，该准则函数P越小，说明该原则下的K-means算法分类越好。

使用某航空公司A321机队的V2500发动机数据进行计算，首先进行数据预处理，即去除粗大误差和进行数据平滑化处理，然后将其中13台发动机的EGTM数据进行聚类分析。如图1所示，当K=4时，准则函数取最小值，认为分4类最合理。

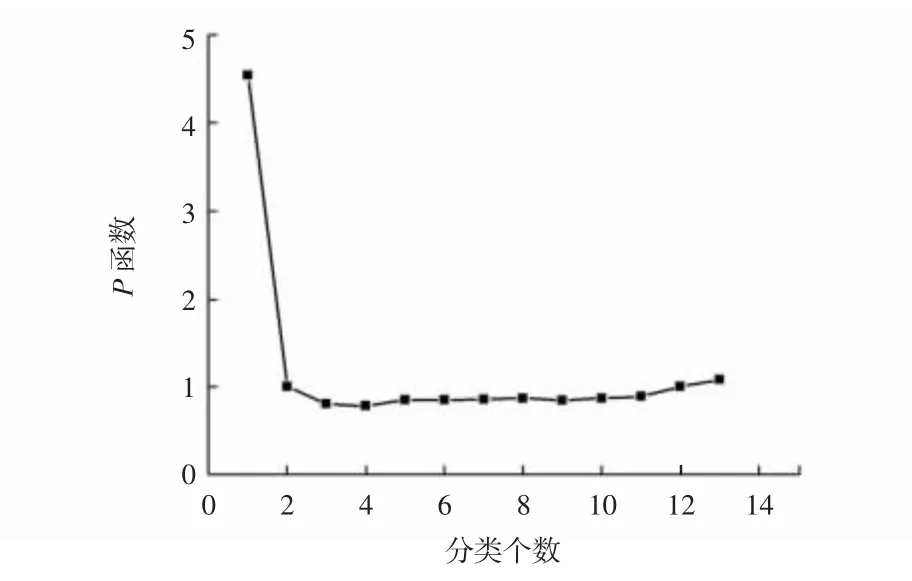
图1 P准则函数图Fig.1 P function

4类的聚类中心如图2所示。根据剩余两台发动机EGTM的历史数据将其匹配到距离最小的类中，根据该类的变化趋势预测该发动机的性能衰退。

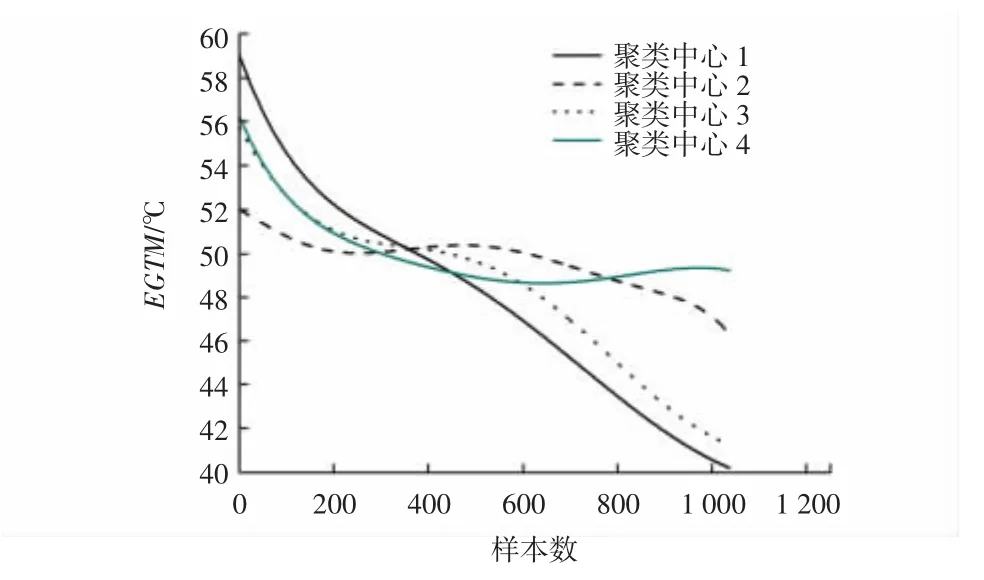
图2 聚类中心图Fig.2 Clustering center

以前750次循环数据为基础，预测第1 036次循环时EGTM的数值，将其结果与单机预测中的线性拟合法、分段线性拟合法、灰色预测法相比较，如表1所示。发现聚类分析的K-means算法预测准确度较高，平均误差下降至3%左右。

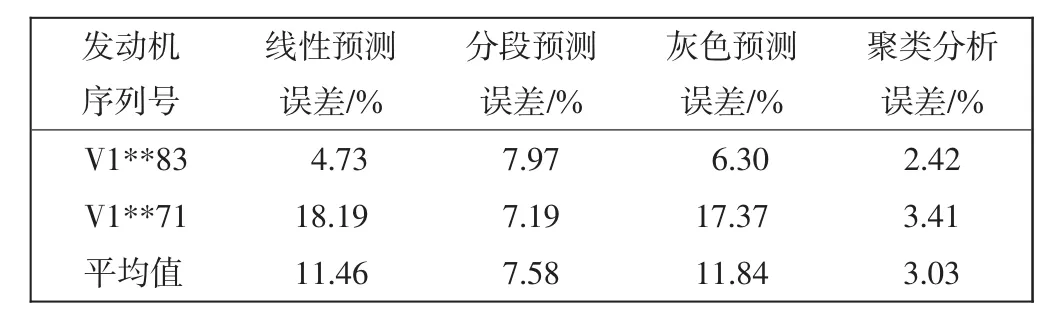
表1 预测结果对比Tab.1 Comparison of prediction results

2 机队下发方案优化

得到机队中每台发动机的下发时间后，如何合理安排每台发动机的下发时间，是机队下发方案优化要解决的问题。随着机队规模的扩大，若采用遍历方式寻找最优机队下发方案需要极大的运算规模。目前有基于排序原则的LPT（longest processing time），SPT（shortest processing time）、FCFS（first come first serve）等启发式方法进行优化，但这些算法并不十分适用于机队下发方案的优化。机队的下发方案是个较为复杂的问题：①各个发动机是可以反复修理、多次使用的装置，因此单台发动机的下发将影响该发动机送修期间的下发方案；②每台发动机由于自身衰退特性导致下发的期限各不相同；③计划初期的不同下发方案决策对计划中后期会产生较大影响。

研究基于以下假设：

1）发动机分配到不同飞机上不影响在翼寿命；

2）各发动机的各次在翼寿命已由预测方法得到；

3）送修周转时间相同；

4）在翼时间不可中断，飞机缺发时不允许飞机停飞，并把租发作为缺发唯一的解决方案，优化目标是在计划期内机队缺发时间最小。

如图3所示，对发动机下发问题进行具体分析，假设发动机送修周转时间是Tm，如果机队中任意两台发动机的下发时间间隔ΔT大于Tm，前一个下发的发动机会在下一台发动机下发之前返回，并作为备发，理论上整个机队只需要1台备发就能保证全机队无缺发。

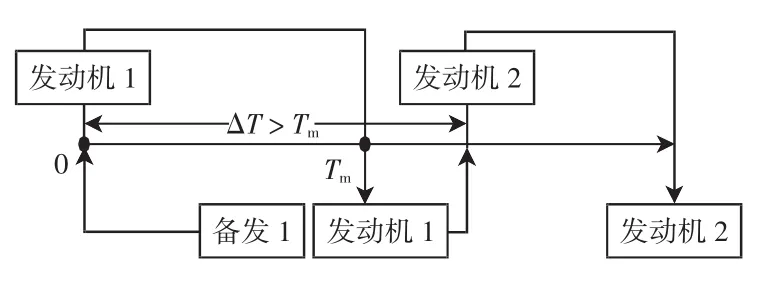
图3 机队下发间隔分析图Fig.3 Engine removal interval analysis

然而实际情况，机队下发间隔并不能都保持大于Tm，大多时候都小于Tm，因此提出间隔控制算法（IC，interval control），希望在未来一段计划期内对机队发动机下发间隔进行控制，使间隔靠近Tm，以此保证缺发时间最小。在选择备发时，采用优先强度概念决定备发的优先级别。

定义1优先系数

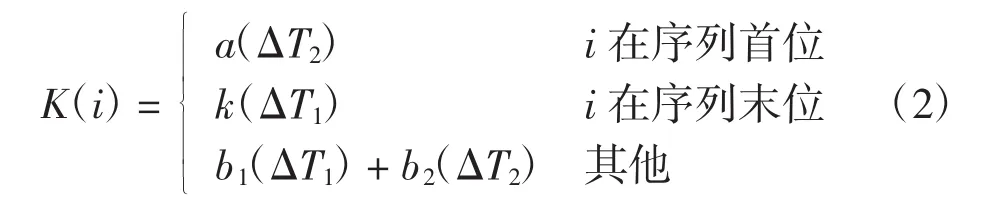
其中：i为备用发动机编号；ΔT1为该发动机根据在翼寿命排序后与前一台发动机的下发间隔；ΔT2为与后一台的下发间隔；a、k、b1、b2为惩罚因子函数，由前后下发间隔与送修周转时间决定。K（i）值越大，则越优先。

定义2优先矩阵

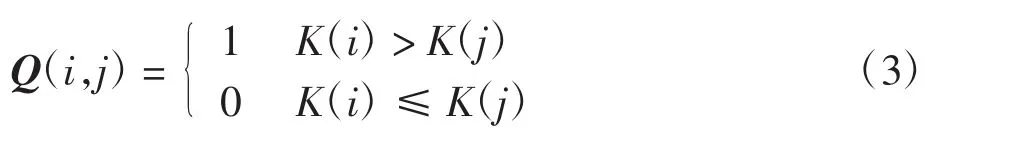
其中：i，j为备用发动机编号。当备发i优先于备发j时，Q（i，j）=1。

定义3优先强度

对备发i遍历所有备发，计算该备发优先于其余备发的次数，作为其优先强度。

使用文献[7]中的数据进行计算，以某航空公司发动机机队为研究对象，该机队拥有10架双发飞机，20个机位，25台发动机，其中20台在翼，5台为备用发动机。计划期截取2000年01月至2003年12月，共Q=1 423个工作日，平均送修周转时间T=60天。

如图4所示，算法主程序为：

1）设定时钟，代表时间的推进。

2）设定矩阵Mengine（编号，发动机寿命，送修次数，状态），表示发动机参数，状态分为可用/送修；设定矩阵Mfleet（编号，发动机号，在翼剩余时间，状态），表示机位参数，状态分为正常/缺发；设定矩阵Mlack（缺发次数，缺发机位，缺发开始时间，缺发结束时间，持续时间），用于统计缺发数据；设定矩阵Mrpl（编号，发动机机号，送修次数，下发时间，送修返回时间），用于记录送修数据。

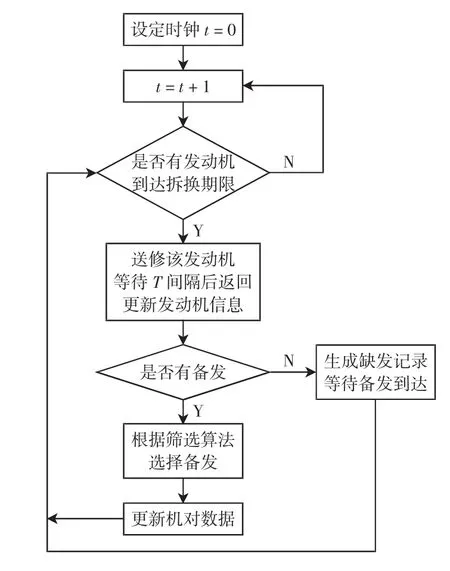
图4 下发规划总流程图Fig.4 Flow chart of removal plan optimization

3）当时间推进1天时，遍历Mfleet矩阵下各机位的发动机在翼剩余时间，若存在发动机在翼剩余时间为0，则在矩阵Mengine中将该发动机变更为送修状态，并且于t+60时间后才能返回，同时生成拆换记录Mrpl。

4）同时该机位需换上备发，如无备发，则生成缺发记录Mlack，该机位等待备发到达。若有备发，则根据不同的筛选原则，选择最适合的备发装上机位，同时更新矩阵Mengine和矩阵Mfleet。

5）循环直至结束。

备发筛选算法使用SPT、LPT、FCFS和间隔控制算法。前3种算法不再详述，间隔控制算法流程如图5所示：

1）依次将每台可用备发加入机队中，根据在翼剩余时间进行排序；

2）计算该备发在序列中的前后间隔，利用式（2）～式（4）计算优先强度；认为下发间隔小于周转时间的负面影响将大于下发间隔大于周转时间的正面影响，因而增大其相关权重，惩罚因子函数设定为

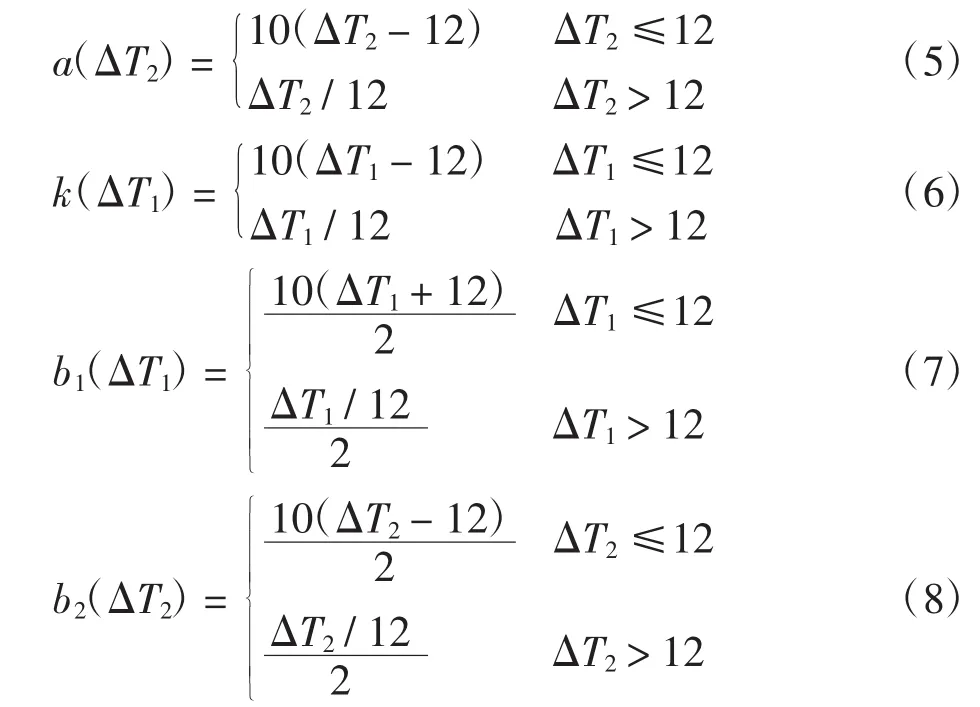
3）选择优先强度高的备发装上机位。

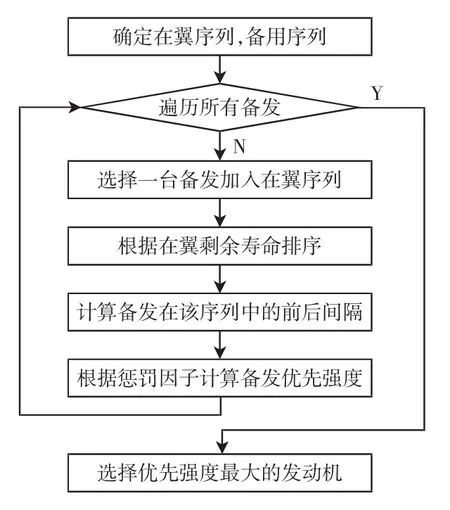
图5 间隔控制算法流程图Fig.5 Flow chart of interval control algorithm

最终计算结果如表2所示。可以看出，在该计划期内，相比SPT、LPT、FCFS算法，间隔控制算法的缺发时间最少，在该算例下可达到0缺发时间，使得总成本最低，确保航空公司的经济效益，验证了间隔控制算法的有效性。

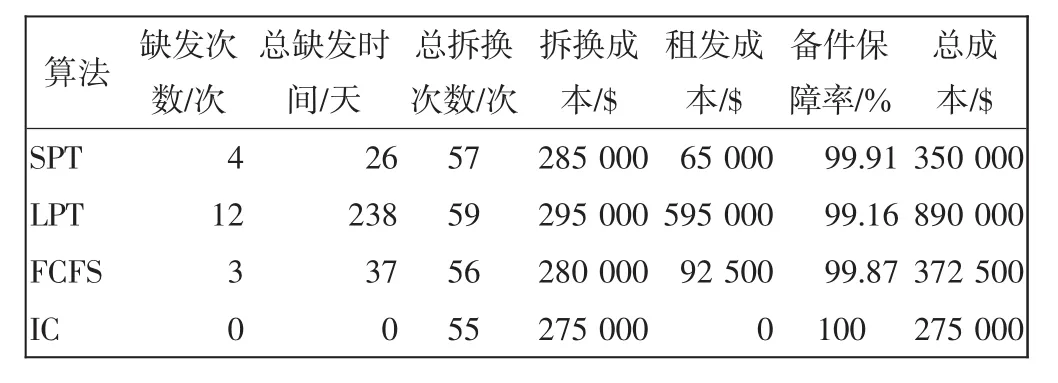
表2 筛选算法结果对比Tab.2 Comparison of different sorting results

不同算法的发动机季度拆换次数的对比如图6所示。经计算，间隔控制算法的拆换率方差最小，更为平滑，如表3所示，这也验证了文献[14]中的拆换率不平衡是引发高成本的因素以及平滑拆换率可以降低成本的观点。

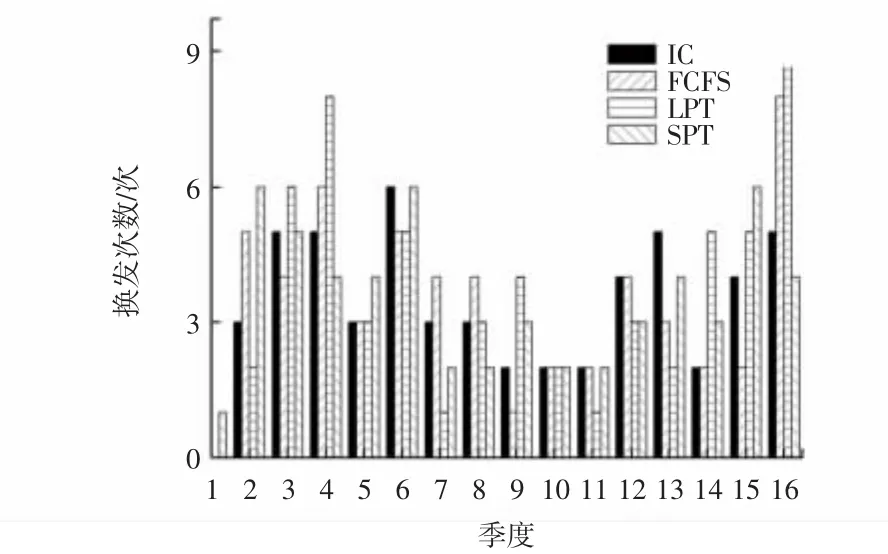
图6 发动机季度拆换次数直方图Fig.6 Engine removal times histogram

表3 标准差对比Tab.3 Comparison of standard deviations

3 结语

1）为了对发动机由于性能衰退导致的下发进行预测，以EGTM为参数，使用聚类分析的K-means方法进行预测，并针对K-means方法不能对分类数进行评价的缺陷，提出了判别函数。相比于单机EGTM预测，该方法精度更高，有利于航空公司更准确地预测发动机由于性能衰退导致的下发时间。

2）基于下发间隔的优先系数，选择备用发动机，利用间隔控制算法实现了发动机机队下发方案的优化。结果表明，相对于在线排序算法优化，该方法更适合于发动机机队下发方案的优化，能更好地减少缺发时间，从而降低机队运行成本。

参考文献：

[1]彭鸿博,刘孟萌,王悦阁.基于起飞排气温度裕度(EGTM)的航空发动机寿命预测研究[J].科学技术与工程,2014,14(16)：160-164.

[2]左洪福,张海军,戎 翔.基于比例风险模型的航空发动机视情维修决策[J].航空动力学报,2006,21(4)：716-721.

[3]任淑红.民航发动机性能可靠性评估与在翼寿命预测方法研究[D].南京：南京航空航天大学,2010.

[4]富 涛,许春生.在翼航空发动机剩余寿命预测[J].中国民航飞行学院学报,2006,17(3)：18-21.

[5]赵玉婷.民航发动机在翼寿命预测模型方法研究[D].南京：南京航空航天大学,2010.

[6]JOO S J.Scheduling preventive maintenance for modular designed components：A dynamic approach[J].European Journal of Operational Research,2009,192(2)：512-520.

[7]白 芳.民航发动机机群调度优化与视情维修决策方法研究[D].南京：南京航空航天大学,2009.

[8]付旭云.机队航空发动机维修规划及其关键技术研究[D].哈尔滨：哈尔滨工业大学,2010.

[9]王 康.k-means聚类算法的改进研究及其应用[D].大连：大连理工大学,2014.

[10]周世兵,徐振源,唐旭清.K-means算法最佳聚类数确定方法[J].计算机应用,2010,30(8)：1995-1998.

[11]陈宏林,吴先球.粗大误差的灰色判别方法及其应用[J].大学物理实验,2010,23(3)：62-64,68.

[12]唐国春.现代排序论[M].上海：上海科学普及出版社,2003.

[13]张 涛.航空发动机视情调度优化方法及系统开发[D].南京：南京航空航天大学,2009.

[14]HALSMER R A,MATSON R E.Smoothing CFM56 Engine Removal Rate at USAir[C]//Aerospace Ground Testing Conference,Nashville,TN(United States),Jul 6-8,1992-3928：6.

[15]白 芳,左洪福,任淑红,等.航空发动机拆换率平滑方法研究[J].航空动力学报,2008,23(10)：1821-1828.