机床电主轴有限元建模与优化设计

蔡俊琼，曹宏瑞

1 引言

主轴作为数控机床核心部件，其性能高低将影响机床整体发展水平。将主轴与电机合为一体的电主轴相比于传统机械主轴，极大地消除了主轴系统在高速运行时的不平衡和噪声等负面影响，有效改善了主轴高速性能，在数控机床中得到了广泛应用。

与普通机械主轴相比，电主轴动态特性随着转速变化而变化，需要建立与实际物理模型相符的有限元模型[1]。文献[2]中通过有限差分法建立主轴系统数学模型，文献[3]中将轴承划分为有限元单元建立包含壳体、轴承、及转轴等部件的电主轴整体动力学模型。高转速下电主轴动态特性还与刚度和质量密切相关，要求其具有较高的刚度和较轻的质量。文献[4]中通过模型仿真给出了轴承刚度和跨距优化选择方案。文献[5]中开发了一种基于遗传算法的优化方法用于寻找轴承在主轴上的最佳位置。

依据电主轴几何参数和简化原则，基于ANSYS Workbench建立电主轴有限元模型并设计模态测试实验，将分析结论和实验结果应用到电主轴转子高刚性和轻质量优化设计中，经优化后使主轴系统具有更好的静动态特性，提高机床加工水平。

2 几何模型设计与分析

2.1 电主轴主要技术指标

某公司数控成形砂轮磨齿机电主轴主要技术指标，如表1所示。

表1 电主轴主要技术指标Tab.1 Main Technical Parameters of the Motorized Spindle

2.2 电主轴材料参数

该电主轴转子材料为38CrMoAl，热处理方式为调质处理，主要物理参数，如表2所示。

表2 电主轴转子物理参数Tab.2 Physical Parameters of the Motorized Spindle Rotor

2.3 支承形式及冷却方式

支承参数形式为：（1）轴承类型选用陶瓷角接触球轴承；（2）轴承配置形式为背靠背安装；（3）预紧方式为定位预紧；（4）轴承润滑方式为油气润滑。冷却方式采用冷却液冷却，冷却液沿着水套外面凹槽流过整个电主轴壳体，起到降低电主轴温度作用。

2.4 电主轴几何模型

该电主轴主要由砂轮、前端轴承座、电主轴壳体、电机定子和转子、后端轴承座等部分组成。采用三维建模软件ProEngineer建立电主轴装配体几何模型，如图1所示。

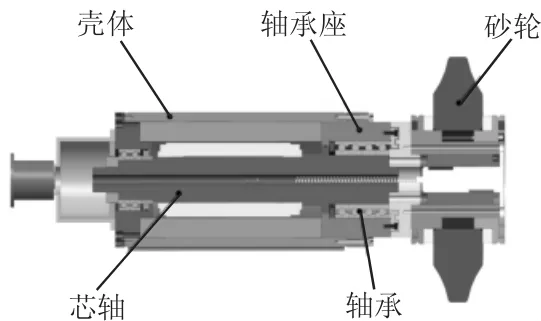
图1 主轴装配体几何模型Fig.1 Geometry Models of the Spindle Assemble

3 电主轴有限元建模

3.1 电主轴几何模型简化

由于电主轴结构复杂以及轴承刚度的时变特性，在仿真分析时需要根据相关简化原则[6]对电主轴几何模型进行简化。

（1）每个轴承用水平和竖直方向4个弹簧单元代替[7]，弹簧刚度由角接触球轴承拟静力学模型计算得到；（2）将主轴定子和装配体上的零件等效为同密度主轴材料；（3）忽略主轴壳体零部件上用来输送油气和冷却水的细小孔道结构；（4）忽略轴承角刚度影响，认为浮动轴承只有径向刚度、角接触轴承只有轴向刚度和径向刚度。

3.2 基于ANSYS Workbench有限元建模

将电主轴几何模型导入ANSYS Workbench，零部件之间设置成Bonded接触关系，采用四面体划分网格，轴承外圈施加固定约束，主轴后端施加周向约束，主轴前端施加径向磨削力载荷，建立起电主轴有限元模型，如图2所示。

图2 电主轴有限元模型Fig.2 Finite Element Models of the Motorized Spindle

4 静力分析与模态分析

4.1 角接触轴承刚度计算

传统电主轴设计计算中，静刚度Kr多由经验公式计算得出[8]，造成计算结果与实际主轴刚度有较大偏差。采用滚动轴承拟静力学模型，可使计算结果更为准确，更符合电主轴实际结构特征[9]。由表3中轴承参数，采用滚动轴承拟静力学模型[10]计算出前端轴承B7016轴向刚度Ka1=161464 N/mm、径向刚度Kr1=343861N/mm；后端轴承B7013轴向刚度Ka2=126268N/mm、径向刚度Kr2=268714N/mm，将计算的轴承刚度值作为有限元模型中等效弹簧刚度。

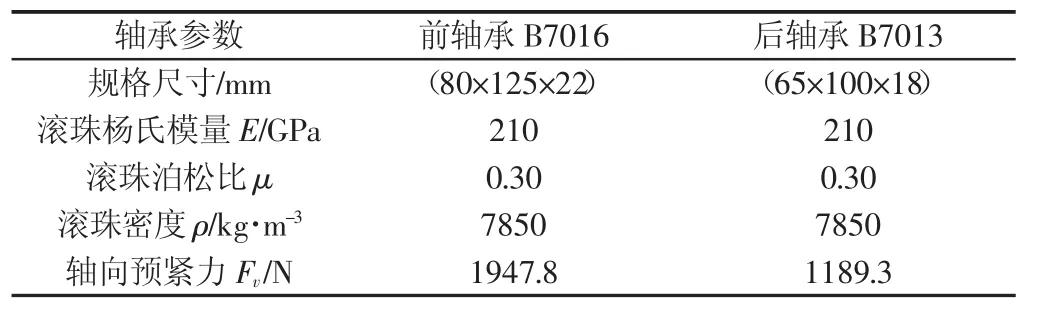
表3 前后端轴承各项参数Tab.3 Parameters of the Front and Rear Bearing

4.2 轴端径向磨削力及初始位移

由式（1）可计算出该磨削电主轴轴端受到的磨削力大小。

式中：P—电主轴额定功率；d—轴端砂轮直径；n—电主轴转速。

已知电主轴功率P=30 kW，转速n=4000 r/min，砂轮直径d=330 mm，代入式（1）中计算得F=434 N。再结合4.1中求出的轴承刚度以及建立的有限元模型可计算出轴端产生的径向位移为4.185μm。

4.3 电主轴模态分析

在自由状态下，前6阶为6个自由度刚体位移振动，这里只考虑（7～10）阶模态振型和固有频率，在ANSYS Workbench中将分析阶数设定为前10阶，计算结果，如表4、图3所示。

表4 电主轴7～10阶固有频率Tab.4 7th to 10th Order Natural Frequencies of the Motorized Spindle

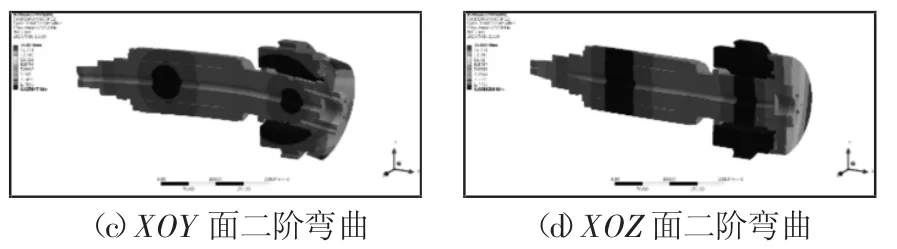
图3 电主轴7～10阶模态振型Fig.3 7th to 10th Order Modal Shapes of the Motorized Spindle

由计算结果知7、8阶模态振型为两个相互正交平面内一阶弯曲振动；9、10阶模态振型为两个相互正交平面内二阶弯曲振动。

4.4 电主轴转子实验研究

为验证建立有限元模型动态响应是否与实际电主轴相符，设计频响函数敲击实验，测量电主轴转子在自由状态下固有频率和相应模态振型。实验仪器和设备参数列表，如表5所示。

表5 实验仪器和设备参数列表Tab.5 Parameter List of the Experimental Apparatus and Equipment

将该电主轴用柔性绳索悬挂使其处于自由状态，在主轴前端和后端分别贴上加速度传感器，用力锤敲击主轴前端和后端，传感器布置方式和数采仪器接线方式，如图4所示。将亿恒数据采集仪采集到的数据文件导入到MatLab中进行分析得到电主轴转子频率响应函数，如图5所示。仿真结果与实验结果对比，如表6所示。

图4 测量电主轴转子自由状态下频率响应Fig.4 Testing the Frequency Response of the Motorized Spindle in Free State

图5 电主轴转子频响函数Fig.5 Frequency Response Function of the Motorized Spindle

表6 仿真结果与实验结果对比Tab.6 Comparison of the Simulation and Experiment Results

对比结果表明计算的一阶频率比实验结果略低，误差产生原因可能有：（1）建立有限元模型时采用了简化原则和理想假设，忽略了细小孔道和螺纹等结构；（2）加速度传感器自身误差及实验仪器安装误差的影响；（3）没有考虑接触面接触刚度和阻尼的影响；（4）用弹簧代替轴承时忽略了轴承游隙，造成了系统动力学特性偏差；（5）实验采用柔性绳索悬挂方式，并非完全自由边界条件。

5 高刚性、轻质量优化设计

5.1 优化设计参数分析

（1）设计变量。根据该磨削电主轴实际功能结构和优化设计指标需求确定设计变量变化范围。（2）状态变量。芯轴质量m，轴端位移δ，一阶固有频率f、最大应力σ。（3）约束条件。轴端径向位移不超过初始值；最大弯曲应力不超过许用切应力。（4）目标函数。一阶固有频率提高10%并取最大值；芯轴质量减轻10%并取最小值。优化设计参数分析，如表7、表8所示。

表7 设计变量取值范围Tab.7 Value Ranges of the Design Variables

表8 状态变量、约束条件和目标函数Tab.8 Status Variables，Constraint Conditions and Objective Function

5.2 优化设计结果分析

分别采用ANSYS Workbench的4种优化算法：遍历搜索算法（Screen）、多目标遗传算法（MOGA）、多目标自适应算法（AMO）和基于响应面优化算法（RSO），优化结果，如表9所示。

表9 优化设计结果Tab.9 Results of the Optimization Design

基于响应面算法（RSO）优化结果较差，另外三种算法优化结果中，一阶固有频率相差不大，均在1050Hz附近，其中遍历搜索算法（Screen）优化得到的质量减轻效果较差，，从多目标遗传算法（MOGA）和多目标自适应算法（AMO）优化结果看，前者质量小但一阶固有频率也稍低，后者一阶固有频率高但质量也稍大，依据优先考虑高刚性设计要求，这里将多目标自适应算法（AMO）优化结果作为最优解。优化前后目标参数值比较，如表10所示。

表10 优化前后目标参数值比较Tab.10 Comparison of Goal Parameters Between Before and After Optimization

优化结果表明，通过此次优化设计将芯轴一阶固有频率从792.37Hz增大到1059.5Hz，提高了33%；将芯轴质量从21.7kg减小到17.214kg，减轻了21%，达到了高刚性和轻质量优化设计要求。

6 结论

基于有限元建模理论和滚动轴承拟静力学模型建立电主轴有限元模型，计算了轴承刚度和主轴系统静刚度，提取（7～10）阶固有频率和模态振型以及主轴在受到径向切削力条件下的静态位移，以此作为初始条件对电主轴转子进行高刚性和轻质量优化设计，分析四种不同优化算法特点和效率。针对某公司磨削电主轴，对其进行有限元建模与高刚性、轻质量优化设计，使优化后的一阶固有频率提高33%，质量减轻21%，实现了电主轴转子高刚性和轻质量优化设计目标。

参考文献

［1］曹宏瑞，李兵，何正嘉.高速主轴动力学建模及高速效应分析［J］.振动工程学报，2012，25（2）：103-109.

（Cao Hong-rui，Li Bing，He Zheng-jia.Dynamic modeling of high-speed spindles and analysis of high-speed effects［J］.Journal of Vibration Engineering，2012，25（2）：103-109.）

［2］Bollinger JG，Geiger G.Analysis of the static and dynamic behavior of lathe spindles［J］.International Journal of Machine Tool Design and Research，1964，3（4）：193-209.

［3］Cao Y，Altintas Y.A general method for the modeling of spindle-bearing systems［J］.Journal of Mechanical Design，2004，126（6）：1089-1104.

［4］Sharan AM，Sankar S，Sankar TS.Dynamic analysis and optimal selection of parameters of a finite element modeled lathe spindle under random cutting forces［J］.Journal of Vibration and Acoustics，1983，105（4）：467-475.

［5］Lin CW.Optimization of bearing locations for maximizing first mode natural frequency of motorized spindle-bearing systems using a genetic algorithm［J］.Applied Mathematics，2014，5（14）：2137-2152.

［6］吴玉厚，饶良武，赵德宏.陶瓷球轴承电主轴的模态分析及其振动响应试验［J］.机械设计与制造，2011（12）：219-221.

（Wu Yu-hou，Rao Liang-wu，Zhao De-hong.Modal analysis and vibration response test for motorized spindle of ceramic ball bearing［J］.Machinery Design&Manufacture，2011（12）：219-221.）

［7］裴大明，冯平法，郁鼎文.基于有限元方法的主轴轴承跨距优化［J］.机械设计与制造，2005（10）：44-46.

（Pei Da-ming，Feng Ping-fa，Yu Ding-wen.Optimum design of spindle bearings distance based on FEM［J］.Machinery Design&Manufacture，2005（10）：44-46.）

［8］宋春明，何宁，张士勇.高速角接触陶瓷球轴承径向刚度的分析计算［J］.机电产品开发与创新，2007，20（4）：31-32.

（Song Chun-ming，He Ning，Zhang Shi-Yong.Analysis and calculation on radial rigidity of high speed angle contact ceramic ball bearing［J］.Development&Innovation of Machinery&Electrical Products，2007，20（4）：31-32.）

［9］曹宏瑞，李亚敏，何正嘉.高速滚动轴承-转子系统时变轴承刚度及振动响应分析［J］.机械工程学报，2014，50（15）：73-81.

（Cao Hong-rui，Li Ya-min，He Zheng-Jia.Time vary bearing stiffness and vibration response analysis of high speed rolling bearing-rotor systems［J］.Journal of Mechanical Engineering，2014，50（15）：73-81.）

［10］曹宏瑞，何正嘉，訾艳阳.高速滚动轴承力学特性建模与损伤机理分析［J］.振动与冲击，2012，31（19）：134-140.

（Cao Hong-rui，He Zheng-jia，Zi Yan-yang.Modeling of a high-speed rolling bearing and its damage mechanism analysis［J］.Journal of Vibration and Shock，2012，31（19）：134-140.）