岩矿石稀土特征线性关系的新发现及其应用

钱惠萍,丁卫平

(1 安徽省地球物理地球化学勘查技术院， 安徽合肥 230022； 2 中化地质矿山总局地质研究院, 河北涿州 072754 )

0 引言

稀土数据在确定岩矿石来源，分析岩矿石成因方面有很重要的作用。稀土元素在工业上的作用更是不可限量，做为一种工业的维生素，它们受到广泛的应用，对其研究有很重要的意义。地质工作者在进行矿产调查工作中，通过对地理上相距较远的三个地区的各类岩矿石的总稀土量与轻稀土总量的关系研究，发现不同岩矿石类型对稀土的富集程度明显不同，确认在岩矿石中存在总稀土量与轻稀土总量的线性关系，该线性关系是比较稳定的关系，希望引起地质工作者的注意和重视。

1 不同地区稀土数据分析

1.1 内蒙古西乌珠穆沁旗火成岩稀土数据分析

研究项目为内蒙古锡林浩特盟西乌珠穆沁旗1∶5万地质矿产调查，区内出露二叠纪流纹岩、玄武岩，侏罗纪火山岩，另外还有不少侵入岩和次火山岩，为了研究其成因，采集多个稀土化学样，分析结果见表1，并计算出轻稀土总量和总稀土量，轻稀土所包含的元素为La、Ce、Pr、Nd、Sm、Eu。重稀土为Gd及以后的元素，不包括Y（钇）元素（稀土含量单位为10-6，下同）。

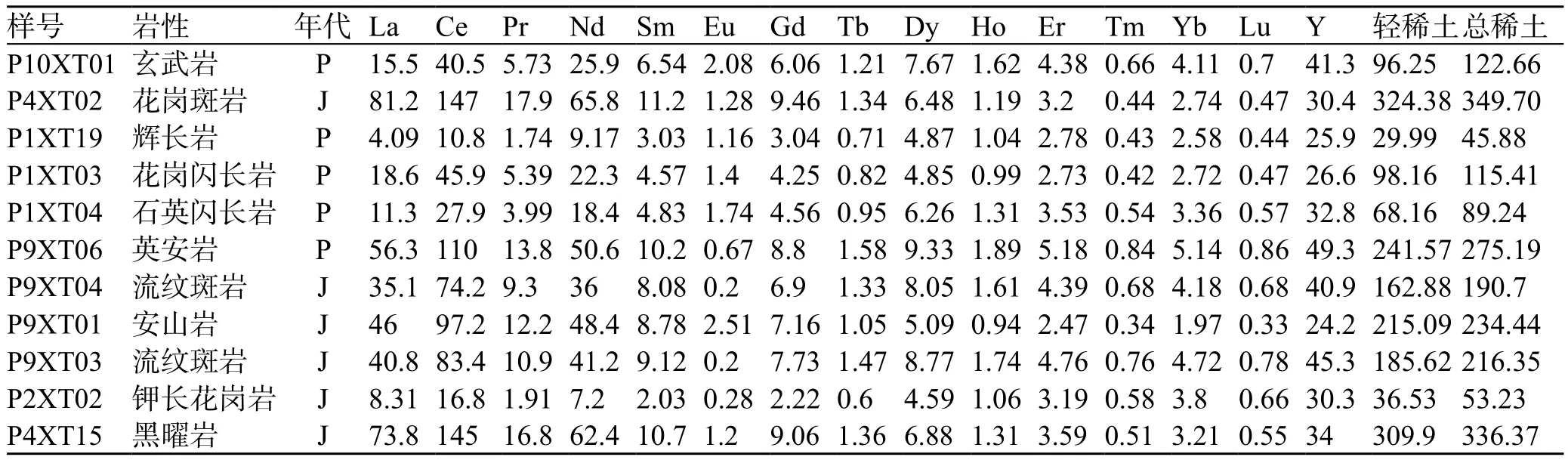
表1 内蒙古西乌珠穆沁旗火成岩稀土数据Table 1 Rare earth data of igneous rocks in the Xiwuzhumuqin Banner, Inner Mongolia

轻稀土量和总稀土量做交汇图(图1)：

由图可见，总稀土量与轻稀土总量之间线性关系明显，相关系数达到了0.999。通过一元线性回归的方法，计算出了最佳拟合于这些点的拟合直线，得到了总稀土量与轻稀土总量的线性关系：即ΣREE=17.76037 + 1.03828ΣLREE。下面利用该线性关系式计算：在只知道轻稀土量的情况下，计算出稀土总量，将其与实际的稀土总量比较，计算出其准确度。准确度的定义如下

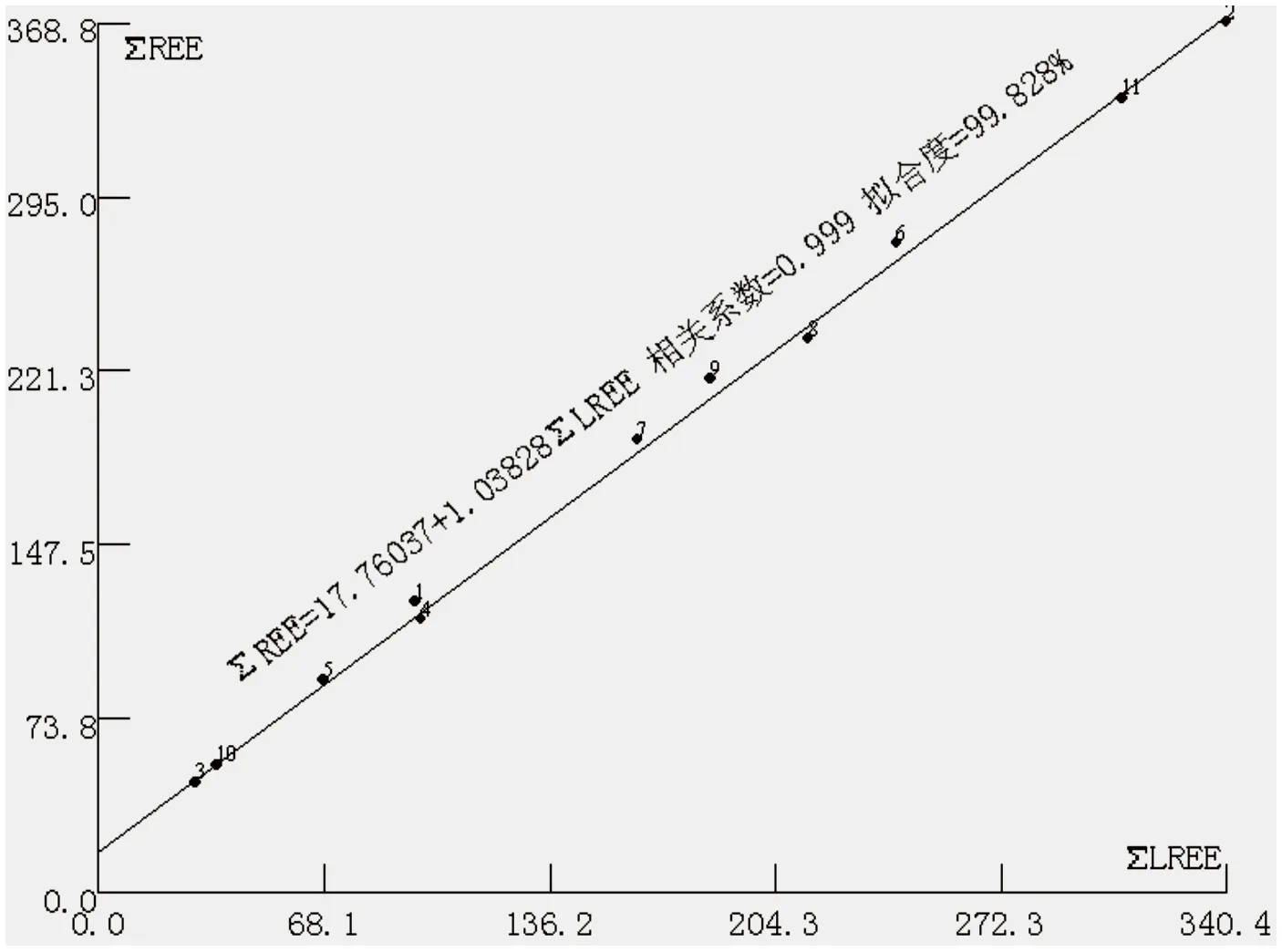
图1 西乌珠穆沁旗火成岩稀土总量与轻稀土量交汇图Fig.1 Crossplotting of total amount of REE with LREE in igneous rock from the Xiwuzhumuqin Banner

RSD(%)——准确度，T∑REE——实测稀土总量，D∑REE——计算稀土总量

RSD(%)=100-│T∑REE- D∑REE│/ T∑REE*100

可见，利用这一线性关系式可以确定每一样品准确程度，将所有结果平均，可得平均的准确程度(表2)。

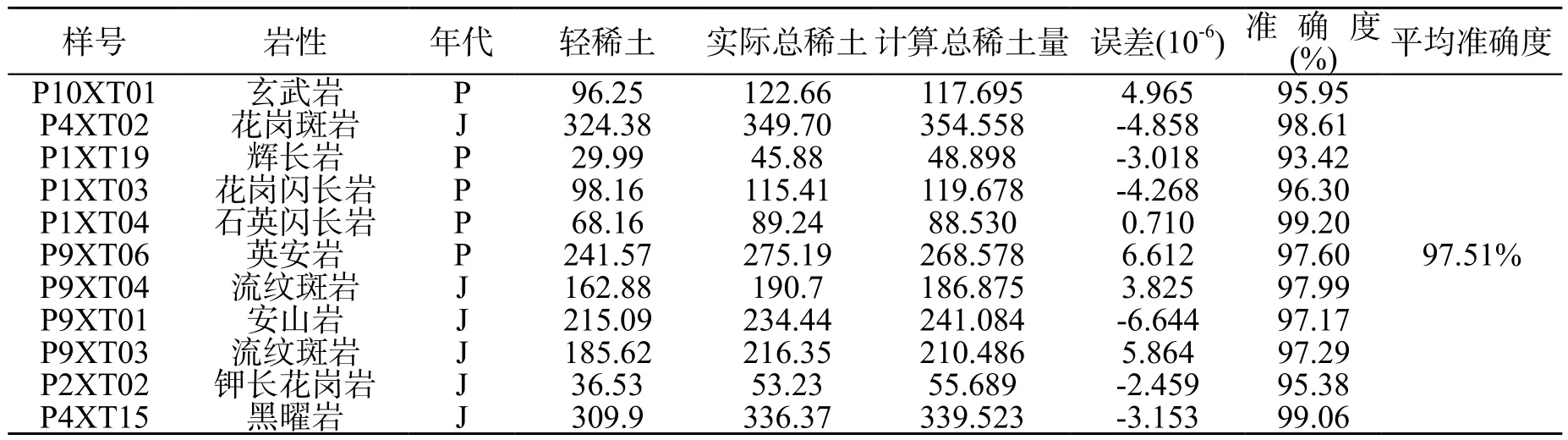
表2 内蒙古西乌珠穆沁旗总稀土量预测准确度表Table 2 Forecast accuracy of total rare earth in the Xiwuzhumuqin Banner, Inner Mongolia

由上表可见，利用一元线性回归方法计算求出的线性关系式来推测稀土总量，其平均准确度高达97.51%，应该说是相当准确的。

1.2 内蒙古四子王旗火成岩稀土数据分析

研究项目为内蒙古四子王旗区域地质矿产调查，四子王旗距锡林浩特的西乌珠穆沁旗相距约500km，同样存在火山和岩浆活动，大地构造上都在大兴安岭南端西北坡一带，是火山岩浆活动发育的地区，为古太平洋板块向东西伯利亚板块的碰撞带。在该区取14件稀土岩石样，分析测试结果表明：

总稀土量与轻稀土总量之间的线性关系明显，两变量的相关系数达到0.996,利用一元线性回归的方法计算出的拟合线，其拟合度达到99.129%。由此得到总稀土量与轻稀土总量的线性关系式：

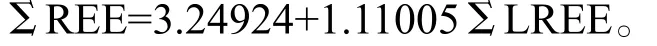
利用一元回归方法计算出的总稀土量与轻稀土总量的关系式来推算总稀土量其准确度也高达9 8%以上。比较一下，用西乌珠穆沁旗火成岩稀土数据计算出的关系式为ΣREE=17.76037+1.03828ΣLREE，而这里的关系式为ΣREE=3.24924+1.11005ΣLREE，两者主要只在常量上相差14左右，即常数项在计算总稀土量上产生的误差为14左右，而作为轻稀土总量这一变量的系数，一个为1.03828，另一个为1.11005，二者仅相差0.07多，说明两个关系式是很相近的。西乌珠穆沁旗与四子王旗这两个地方，虽然相距约500km，但都处在大兴安岭造山带南段的西坡，地质构造环境类似，两个关系式接近也许与这相似性有关。为了确定该关系式与大地构造到底有没有关系，下面继续引入新疆哈密等地的数据来分析，如果这些数据计算得到的关系式与上述关系式相差很大，说明这关系式与地质环境有一定关系，否则关系比较小。因为新疆离上述两个地方相距达4000多公里，处于不同的地质构造带上。

1.3 新疆铁磷矿调查岩矿石稀土数据分析

在我国重要化工矿产成矿远景区带开展的资源评价项目工作，在新疆哈密和库尔勒一带进行了铁磷矿的调查，取了多个样品。有岩浆岩、沉积岩、变质岩，甚至矿石，岩石类型多样，有的样品位置相距达几百公里，地质构造环境不同，将其轻稀土总量与总稀土量做交汇图，结果显示这些数据也表现出明显的线性关系，相关系数达到0.994。

利用一元线性回归的方法计算出的拟合直线，其拟合度达到98.75%，用同样的研究方法，得到总稀土量与轻稀土总量的线性关系式：ΣREE=-3.85343+1.27981ΣLREE。

采用前面类似的方法，利用这一线性关系计算得到总稀土量的平均准确度为90.95097%。

由此可见，新疆多地岩矿石稀土样进行交汇图分析得出的总稀土量与轻稀土总量的线性关系式推断的总稀土量的平均准确度超过90%，与前面两个地区相比而言，准确度要低一些，其原因在于这些岩石或矿石样分布的范围很分散，尽管地质条件差异大，但准确度也超过90%。结果证明：不同岩石类型、不同年代的岩石，其中的总稀土量与轻稀土总量有明显的线性相关关系，三个地区的线性关系见表3。

表3 不同地点所得到的稀土关系式表Table 3 Rare earth relations obtained from different locations

对比线性关系式可见，常数项有一定差别，分别为17.76037、3.24924和-3.85343，但相对于总稀土量而言并不大，因总稀土量经常达到200～300，个别达到1000（某些超基性岩相对要小）。而轻稀土总量在系数上差别小。因此我们认为，在地球的不同地点，稀土的这个线性关系式虽不同，但差别不明显，可考虑建立一个全球岩矿石的总稀土量与轻稀土总量线性关系式，以此来研究：在掌握了轻稀土总量的情况下如何推测总稀土量。将上面三个地区的所有稀土数据合并起来，来研究其线性关系式。这里只将合并数据后得到的交汇图(图2)及推断准确度表呈现。

由图2可见，大范围样品中的总稀土量与轻稀土总量的线性关系明显，相关系数达到0.991，利用一元线性回归的方法计算出的拟合曲线，其拟合度也高达98.214。线性关系式：

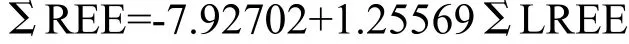
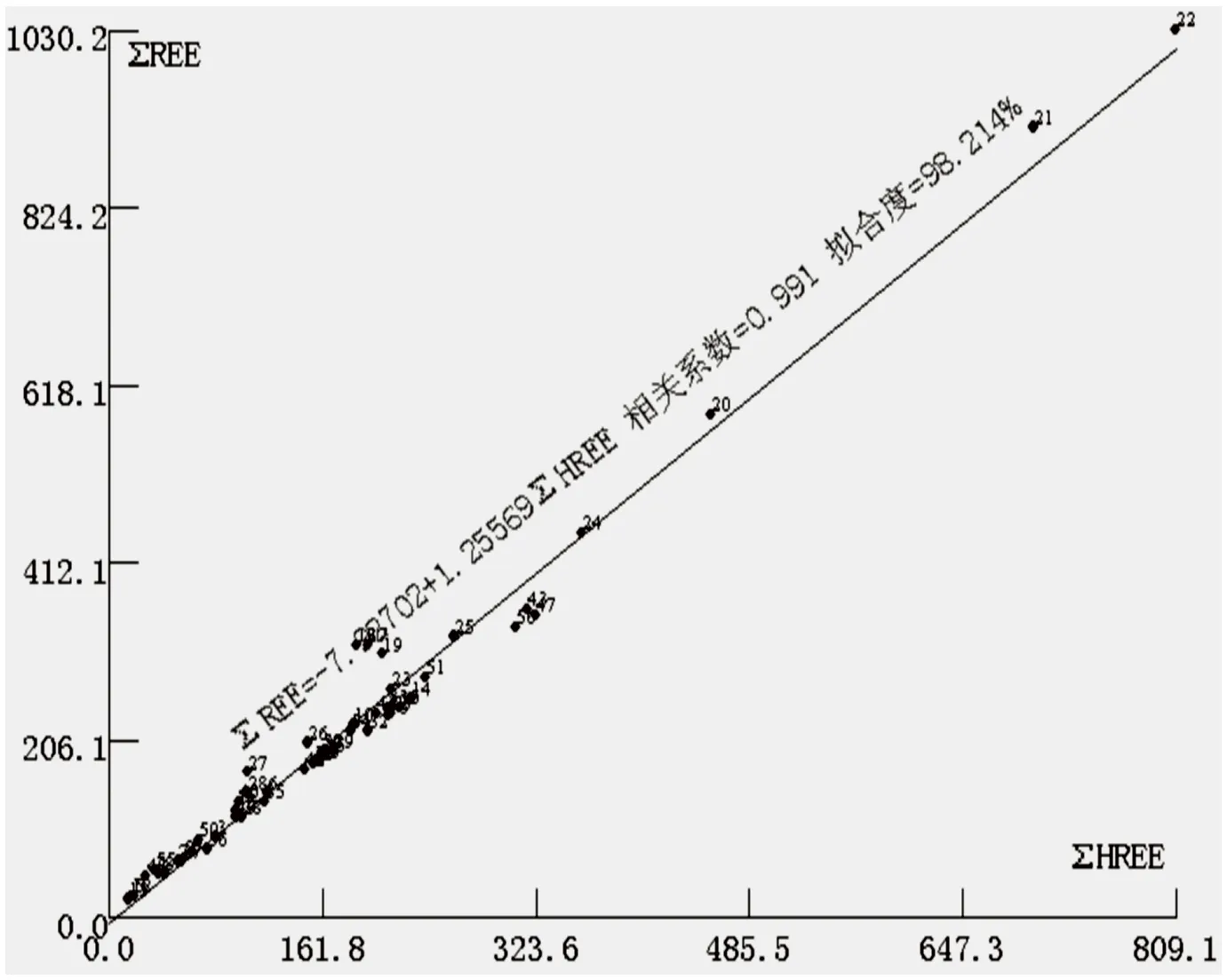
图2 新疆-四子王旗-西乌旗岩矿石样总稀土量与轻稀土总量交汇图Fig.2 Crossplotting of total amount of REE with LREE in rock and ore samples from Xinjiang, the Siziwang Banner, and the Xiwu Banner

利用该线性关系式来计算前面三个地区岩石样中的总稀土量准确度见表4。

上表中所有样品的稀土总量估计准确率接近90%，由于这些样品基本上包含了各种岩石类型，甚至还有矿石，这说明在自然界中任何岩石矿石其总稀土量与轻稀土总量有比较稳定可靠的线性关系。暂考虑地球上岩矿石中的总稀土量与轻稀土总量存在线性关系，该关系式与前面得到的三个地区的关系式有一定差别，但差别不大，由于准确度接近90%，应该是可用的评估关系式。

2 线性关系式的验证

2.1 验证判别矿物中的稀土总量

下面选一些岩石中的矿物稀土样来验证此关系式的可靠性，以下为前苏联学者利亚霍维奇1971年给出的不同成因花岗岩副矿物中的稀土成分表(表5)，后面列出了总稀土量和轻稀土总量。数据来源于南京大学地质系所编的《元素地球化学》。

利用前面计算出:

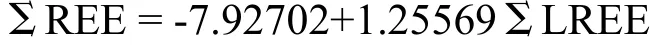
在假如不知道总稀土量的情况下，依据轻稀土总量，计算出总稀土量，与实际总稀土量数据对比，得到每个样的准确度，以及平均准确度见表6。由此可见，矿物中的总稀土量估计的平均准确度达到84.78%，说明该线性关系式可用。这是矿物中的总稀土预测情况，下面对岩石中稀土样来进行预测。

2.2 验证判别岩石中的稀土总量

1983年美国地质调查所确定了八个岩石样的标准浓度，这里选择其中五个样来验证，因这五个样的稀土数据中所有元素都有含量值,其他三个缺乏某些元素的数据。以其中的轻稀土总量，用上述线性公式计算，来估计总稀土量见表7。

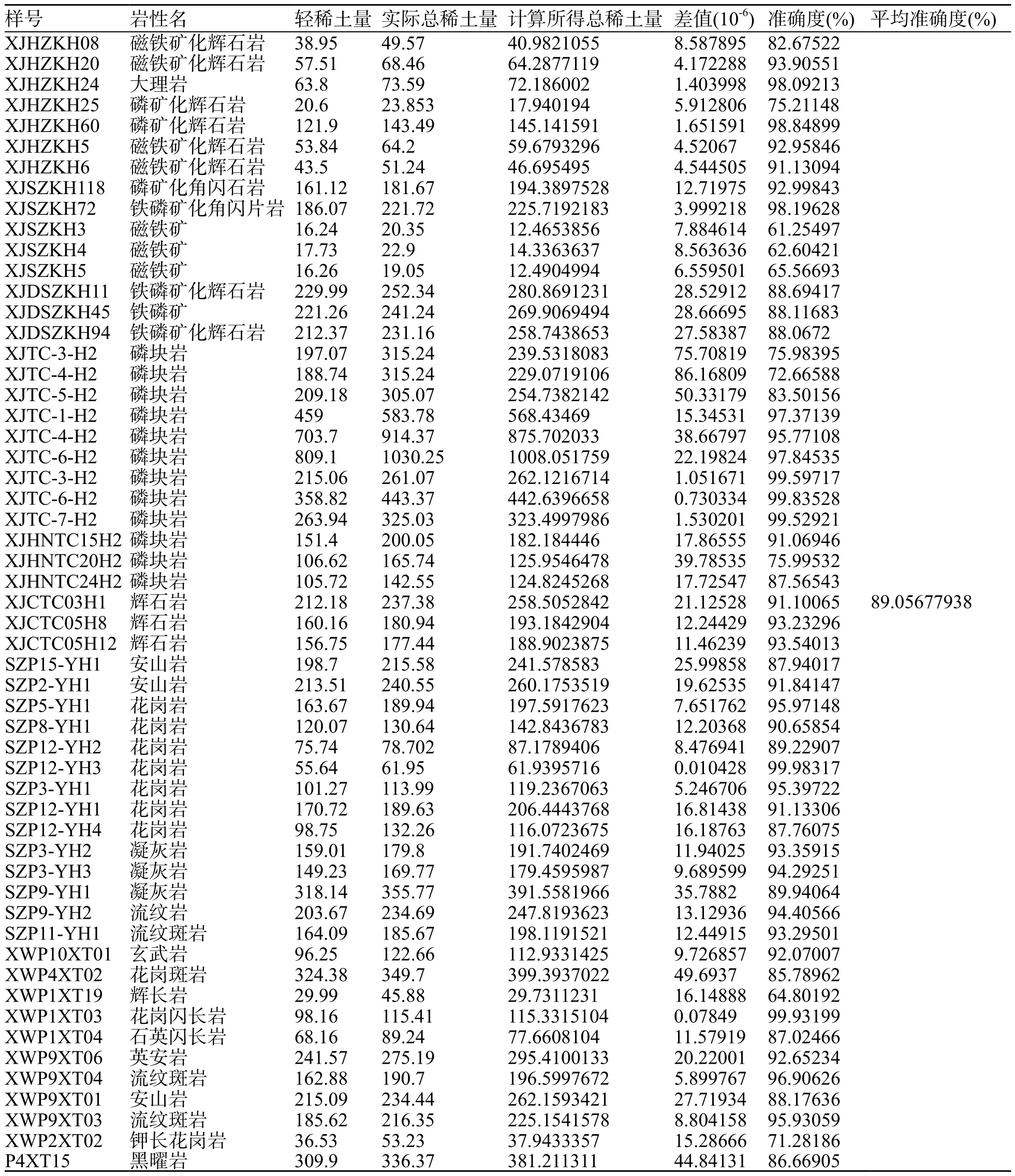
表4 内蒙与新疆等多地区所有样稀土总量估计值准确度表Table 4 Accuracy of rare earth estimates for all samples from many places in Inner Mongolia and Xinjiang

利用轻稀土总量和总稀土量，根据前面求出的线性关系式可以求得五个样总稀土量的估计值，从结果看，估计准确度都超过80%，平均估值为88.70%（表8）。

综不所述，总稀土量与轻稀土总量的关系式ΣREE = -7.92702+1.25569ΣLREE，在地球上所有岩矿石矿物中适用。从准确度来看，可能在矿物中准确性稍差，在岩石中准确性更高。

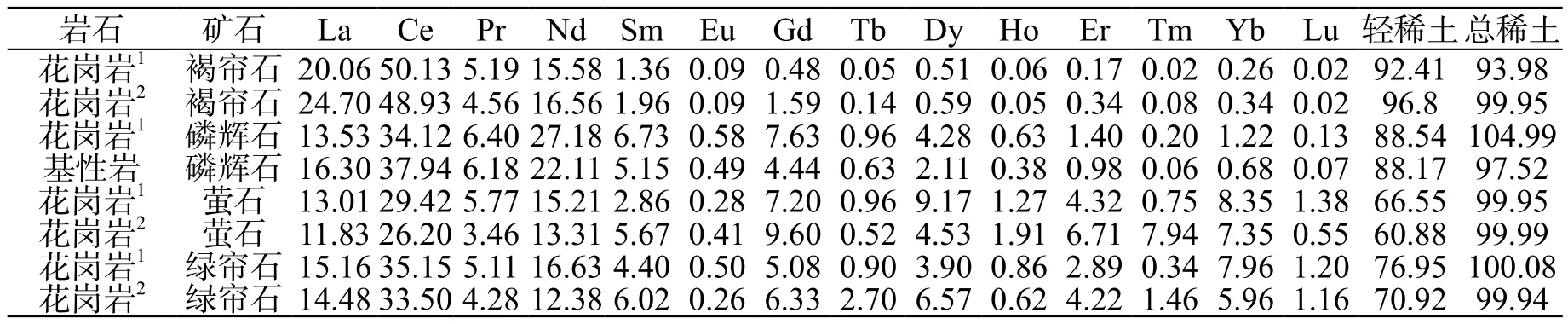
表5 不同成因花岗岩类副矿物中的REE组分及轻重稀土总量 （利亚霍维奇，1971）Table 5 REE components and total amount of light and heavy rare earths in accessory minerals of granite of different origins (After Liakhovich, 1971)

表6 不同成因花岗岩中矿物稀土总量估计准确度表Table 6 Accuracy of rare earth estimates in granite of different origins

表7 美国地质调查所五个岩石标样的稀土浓度表(Glaeeny 等 1983)Table 7 Rare earth concentrations of five standard rock samples from the US Geological Survey (After Glaeeny et al., 1983)

表8 美国地质调查所五个岩石标样总稀土量估计准确度表Table 8 Accuracy of total rare earth estimates in five standard rock samples from the US Geological Survey

2.3 线性关系式的应用

在分析测试过程中，利用ΣREE =-7.92702+1.25569ΣLREE线性关系，可以监控重稀土的分析结果，分析数据是否偏离过大，由上面关系式来约束。因总稀土量减去轻稀土总量就是重稀土总量（不包括Y），另外估算稀土总量时，可以不必分析所有的稀土元素，只要分析前面6个轻稀土元素的含量就能基本估计总稀土量，能降低分析测试成本。

2.4 关系的不适应性

经过试验，发现上述关系式不能用来估算球粒陨石中一些元素含量值，毕竟上述公式是从经过长期地质作用产生的岩石或者矿物中总结出来的，不适应是可以理解的，因球粒陨石相当于地球形成时期的原始物质。

3 讨论

由于总稀土量是轻稀土总量与重稀土总量之和，在得到了总稀土量与轻稀土总量的拟合线后，实际上，重稀土总量与轻稀土总量的拟合线自然也得到了。而任何散点数据都能用回归的方法求出一条拟合直线来，仅仅得到一条拟合线远远不够，关键是拟合度及相关系数也要大，假设总稀土量以y表示，轻稀土总量以x表示，求出的线性关系为y=ax+b,设重稀土量为z，那么，z=y-x=(a-1)x+b,表示轻稀土总量的变量x的系数值在两个关系式中相差1。图3左为总稀土量与轻稀土总量的交汇图，相关系数和拟合度都很大。图3右为重稀土总量与轻稀土总量的关系图，两者求出的拟合线性关系式，常数项相同，都是17.76037，而系数一个为1.03828,另一个为0.03828,相差1，但由于右图的轻稀土总量与重稀土总量的相关系数小，仅为0.664，拟合度更低，小于45%，所以，如果直接用轻稀土总量来推断重稀土总量则误差大，必需先由轻稀土总量来推断总稀土量，再由其差值得到重稀土总量。

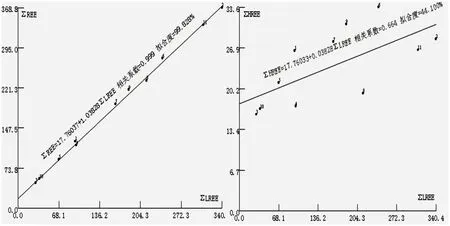
图3 内蒙古西乌珠穆沁旗轻稀土分别与重稀土与总稀土量的交汇图Fig. 3 Crossplotting of LREE respectively with HREE and total REE from the Xiwuzhumuqin Banner, Inner Mongolia

在岩石或矿物中总稀土量与轻稀土总量存在较好的线性关系，与不同的岩石和矿物关系不大，只是在地球的不同地方有些变化，所以才有基本能用于预测的准确度达到80%以上的普遍性线性关系式，关于这种关系式理论上还有待探讨。

参考文献：

[1]刘英俊，曹励明，李兆麟，等.元素地球化学[M].北京：科学出版社,1984.

[2]王中刚，于学元，赵振华，等.稀土元素地球化学[M].北京：科学出版社,1989.

[3]戚长谋.地球化学通论[M].北京：地质出版社,1994.

[4]邱家骧.岩浆岩岩石学[M].北京：地质出版社.1985

[5]丁卫平等.GeoChemSoft的操作及应用[R].

[6]中化地质矿山总局地质研究院.内蒙古四子王旗区域地质调查报告[R].

[7]中化地质矿山总局地质研究院.内蒙古西乌珠穆沁旗白音诺尔农场等四幅区域地质调查报告[R].

[8]中化地质矿山总局地质研究院.我国重要化工矿产成矿远景区带资源评价报告[R].