基于自适应分段广延指数模型的IPTV用户点播行为

陈步华，陈戈，梁洁

（中国电信股份有限公司广州研究院，广东 广州 510630）

1 引言

近年来，随着互联网应用的快速发展和网络技术的不断提升，流媒体技术得到了快速的发展，使得视频点播业务占据了大量的网络带宽。为了降低网络传输压力以及减少带宽限制带来的影响，用户请求的视频内容在经由缓存服务器时会被缓存。当用户对一个视频发起访问请求时，如果其内容已经存储在缓存服务器中，就可以不从远端的源站获取视频而直接从缓存服务器中获取，从而达到降低网络流量的效果，起到降低网络运营成本的作用[1]。然而，缓存服务器的存储空间以及配套资源是有限的，并且过度部署缓存服务器会造成资源和成本的浪费。因此，在视频内容多样性以及用户请求并发性的条件下，优化缓存服务器的系统配置，构建高性能低成本的视频点播系统是非常必要的。基于这种现状的考虑，由于用户对不同视频对象的访问情况总是存在一定的倾向性，因此，研究视频访问的用户行为能够分析出什么类型的内容需要存储在缓存服务器以及存储这些内容需要占用多少存储资源等，从而改善存储资源分配不合理造成的缓存资源不足或者浪费。目前，用户访问行为研究的一项重点工作就是视频的访问热度。

视频访问热度代表了用户对系统中视频文件的观看访问情况，可以根据用户对视频的访问次数来刻画视频访问热度。将视频访问热度具体描述为：在一段时间里，对各个点播视频的用户访问次数进行统计，并对所有视频按照其对应的用户请求次数降序排序，则一个点播视频的访问热度即该视频的位序[2]。

网络协议电视（internet protocol television，IPTV）以网络协议为基础，面向电视终端，通过宽带网向用户提供交互式视频业务[3]，而利用IPTV视频点播服务的访问热度进行深入分析和准确建模，对视频内容的缓存策略设计是十分重要的。因此，改进基于视频热度的拟合曲线的拟合优度就成了改善缓存策略的关键。

在对流媒体用户点播行为的建模研究中，崔华杰[4]采用 Zipf模型进行回归拟合视频的访问热度，后来Guo等人[5]指出Zipf模型无法准确拟合某些自然现象具有的特征，同时，验证了广延指数（stretched exponential，SE）分布模型更适合刻画实际系统视频访问请求次数的分布。广延指数模型最早是由德国物理学家Kohlrausch于1847年提出的。对于其应用，Laherrere等人[6]率先提出，广延指数模型可用于具有重尾现象的自然和社会经济现象的描述中。后来，Guo等人[5]将广延指数模型用于对流媒体系统的研究中，并对比了 Zipf模型的不足之处。因此，对于只采用一种曲线函数回归拟合一段时间内系统中所有的点播视频访问数据难以获得优良的拟合效果，并且对于最常用的曲线拟合求解方法最小二乘法，也有一定的局限性。

因此，本文在对现有IPTV用户视频点播行为的数学模型进行调研的基础上，应用回归分析方法，并以广延指数分布为建模基础，提出了一种自适应分段广延指数（ASSE）模型，用来进行IPTV视频点播行为的模型构建，并提高了视频访问热度模型曲线的拟合优度。

2 视频访问热度模型的构建

回归分析是由英国著名生物学家兼统计学家Francis Galton[7]在研究人类遗传问题时提出来的，用来确定两种或两种以上变量间的具体依赖关系，是建模和分析数据的重要工具。回归分析通过直线或曲线来拟合一些数据点，使得这些数据点到直线或曲线的距离最小[8]。回归属于机器学习中有监督学习的范畴，拟合得出的对应曲线称为回归曲线。用户行为分析也是回归分析拟合应用的重点之一。本节从点播视频的用户的角度出发，利用回归分析，主要针对视频点播中的用户访问行为进行建模与分析，建立系统内一段时间对各视频访问次数的排序和用户对这些视频的访问次数情况之间的函数关系模型。

本文提出的 ASSE模型以广延指数分布为基础，并根据设定的误差阈值β来自适应地分段建模，并满足分段曲线建模的连续性要求。本节将详细介绍基于 ASSE方法的视频访问热度模型的构建过程。

2.1 互补累积概率的计算

本文将拟合视频位序与视频访问互补累积概率之间的关系曲线，其中，互补累积概率的计算方法具体如下：在一个n部IPTV点播视频的系统中，对n部视频的访问概率由高到低排序，依次表示为p(1)，p(2)，…，p(n)，则其对应的互补累积概率为：

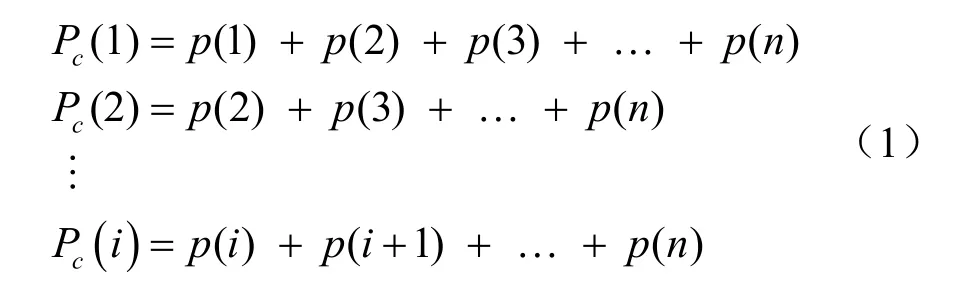
本文选取从中国电信某省 IPTV系统日志中提取的部分数据，视频总数为70 000部，分别统计每一部视频的访问次数，并计算每一部视频的访问概率，再按概率高低依次排序，得出所需要的一串访问概率序列p(1),p(2),…,p(70 000)；然后，根据式（1）计算出视频点播行为的互补累积概率Pc(1),Pc(2),…,Pc(70 000)。

2.2 基础拟合函数的处理

本文采用广延指数分布函数作为基础模型来拟合流媒体系统中用户访问点播视频的情况。广延指数分布的互补累积概率分布函数（complementary cumulative distribution function，CCDF）表示为：

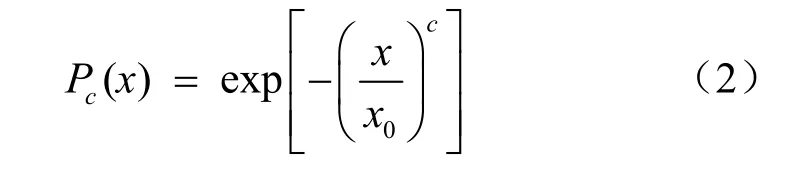
其中，x代表视频位序，Pc(x)代表互补累积概率，x0和c表示两个常量参数，其中x0被称为尺度参数，c被称为广延参数或形状参数。对式（2）取两次对数的通用表达式为：

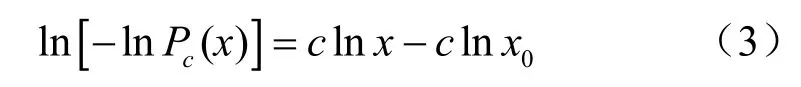
根据式（3）进行坐标转换，简化为线性回归函数模型，如式（4）所示：

其中，Y=ln[-lnPc(x)]，X=lnx，b=-clnx0，x=1, 2, 3,…,n。

2.3 拟合曲线自适应分段

如第2.2节所述，本文采用广延指数函数作为曲线拟合的基础模型。但是，只采用一种函数拟合视频位序与视频访问互补累积概率之间的关系，通常要求自变量与因变量之间有基于该函数的很强的依赖关系，否则，较难得到准确的拟合结果[9]。因此，可以通过将实际数据分成若干组，然后对每组数据再进行拟合的方法提高拟合的精度。拟合线段的条数可以根据具体的工程需求，人工进行设定，也可以采用其他分段方法。本文采用给定一个误差阈值，若连续两次误差平方和高于该阈值，则停止该线段拟合的计算，由此来自适应地确定分段数。具体如下：设定一个误差阈值β，若某数据点A及其下一个数据点B的拟合值和实际值之间的误差平方和均高于该阈值（连续两次误差平方和高于该阈值）则停止该线段拟合的计算，并开始下一段曲线的拟合。

由此，根据阈值误差阈值β，自适应地将实际数据分为m段，对每一段求解的方程如下：

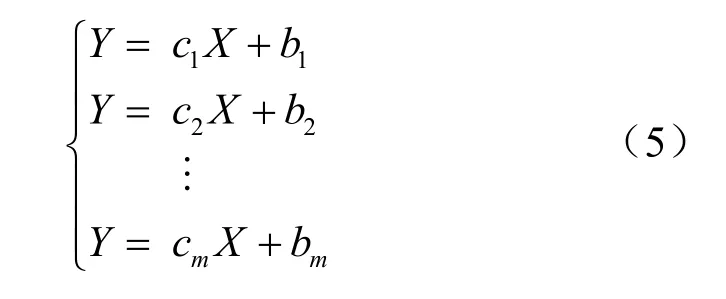
由于曲线分段点处往往不能满足拟合曲线的连续性[10]需求，如图1所示。而且，目前用于解决分段拟合曲线连续性问题的方法均存在局限性。本文给出了一种带约束条件的最优化方案，即在曲线的分段点处，令上一拟合线段的最后一个拟合坐标值，一定落在下一条拟合线段上，作为约束条件。即对于式（5）的每一段的回归模型（即m段曲线模型），令每一段曲线的分段点处的拟合值（X*,Y*）作为该拟合线段的起始点，即满足式（6）：

图1 分段点处拟合值不连续示意

并且在该约束条件下，通过最小二乘法求解出该拟合线段的最优参数c，进而可得b，则将式（5）作为每一段的回归模型，结合式（6），可得：

其中，(X1*,Y1*), (X2*,Y2*),…, (X*m-1,Y*m-1)分别为第1段，第2段，…，第m−1段拟合曲线最后一个拟合点处（分段点）的拟合值。由此，实现了分段点处满足一阶连续的分段曲线拟合，直到所有分段点对应的拟合线段按照此方法建模求解出对应的每一段拟合线段对应的最优参数(c1,b1)，(c2,b2)，(c3,b3)，…，(cm,bm)。至此，建模完成，并且所有数据拟合完毕。

3 实验设计与结果

3.1 实验设置

在 IPTV业务的发展和运营过程中，IPTV系统已经积累了海量用户行为数据。中国电信某省的IPTV系统每天产生近1 TB的数据文件，内容包括用户收视行为日志、系统运行日志等[11]，为对视频点播用户的行为进行建模，从中提取部分数据，包括视频总数70 000部，访问的规律基本满足“二八定律”。基于如此庞大的用户群体及其大量的真实用户记录，可以看出对IPTV CDN用户的行为建模具有足够的代表性与意义。

3.2 仿真结果与分析

因不同视频数量下的 ASSE模的拟合情况均类似，因此，本文不再给出其他不同视频数量下的ASSE模型回归拟合结果。

3.2.1 ASSE模型在不同分段数下的拟合结果

实验采用（X,Y）坐标系，并通过坐标转换，令Y=ln[−lnPc(x)]，X=lnx，其中，x代表视频位序，Pc(x)代表互补累积概率。同时，设定不同阈值β进行自适应分段拟合。图3给出了自适应分段数量（segment）分别为3、5、7、10的情况下，每天用户对点播视频的典型访问情况建模结果如图2所示。通过ASSE模型与实际数据拟合结果对比，可以看出，分段数越高，拟合的吻合程度越高。在分段数≥7的情况下，拟合结果与实际数据具备优良的一致性。

3.2.2 ASSE模型与SE模型拟合结果对比分析

在构建模型的过程中，对模型的优劣评估是十分重要的。本节将通过仿真结果对比本文提出的自适应分段广延指数（ASSE）模型与广延指数（SE）模型的优劣。考虑到分段数不宜过多，并且要兼顾拟合精度，因此，本文选择在分段数为7时，将提出的ASSE模型与SE模型的建模结果进行对比。对比结果如图3所示。

如图3所示，在分段数为7时，提出的ASSE模型比传统的SE模型更符合实际数据的分布。实际数据、SE模型以及ASSE模型拟合出的互补累积概率如图4所示。

图5为实际数据、SE模型以及ASSE模型拟合结果之间的绝对误差。实验结果表明，对于绝大多数数据点的拟合误差，本文提出的 ASSE模型的拟合误差小于SE模型。尤其是对于大约前5 000部访问热片，SE模型拟合的误差远大于ASSE模型。拟合误差越大，就越会导致用户访问流量的错误估计，进而导致对缓存设备的并发流量服务能力估计错误，并对缓存设备的系统并发服务能力配置有很大影响。此外，为了尽可能提高系统资源的利用率，对于访问概率不同的视频，会依据访问概率而设定该视频的缓存时间，通常来说，访问概率高的视频常常比访问概率低的视频的设定的缓存时间要长一些。所以，在对用户视频访问行为预测中，拟合精度对视频缓存的保留时间有着很大影响，进而影响预缓存策略。因此，本文提出的 ASSE模型由于提升了用户访问情况的拟合精度，对服务器的系统配置和热片内容的预缓存策略的改善十分重要。

图2 用户对点播视频的典型访问情况建模结果

图3 两种模型的建模结果与实际数据的对比

图4 互补累积概率拟合结果

图5 两种模型的建模的误差结果的对比

此外，可以通过标准的检验方法来定量评估实际数据与回归模型的拟合程度，拟合优度是一种用来检验实际数据是否符合某个回归拟合模型的统计方法[12]。因此，采用拟合优度检验来检验本文提出的ASSE模型，并与SE模型进行进一步对比，由此来判断模型的拟合效果，这两种模型拟合的检验结果见表1。

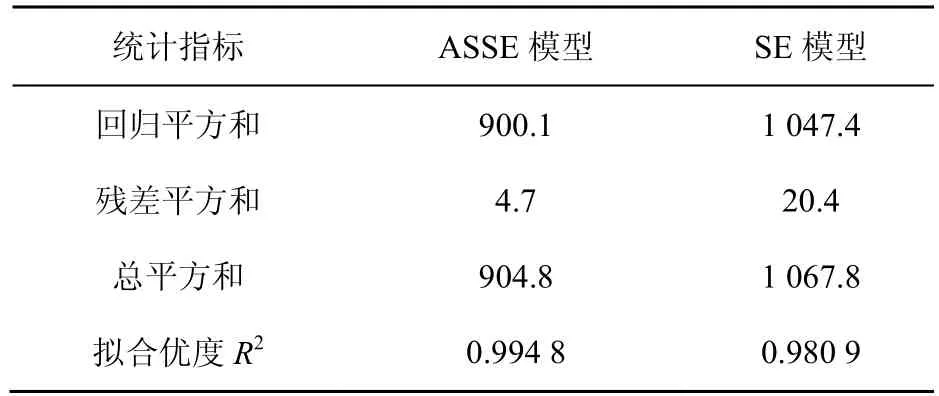
表1 ASSE和SE拟合模型检验结果

由于R2越靠近1，表示实际样本数据越靠近拟合模型，即拟合优度越高。因此，从表1中可以看出，ASSE模型的拟合优度0.994 8髙于SE模型的拟合优度0.980 9。由此进一步说明，本文提出的ASSE模型不仅提高了曲线拟合的精度，并且与实际数据具有良好的一致性。基于此，本文提出的ASSE模型比SE模型更适合对IPTV用户点播行为进行建模，并且能够优化系统配和改善视频调度与缓存策略。

4 结束语

IPTV服务的发展趋势是面向更庞大的用户群和存储更巨大的视频数据，并为用户提供更优质的视频体验。在这种趋势下，IPTV服务所面临的主要挑战是如何优化IPTV CDN的系统性能，并同时降低部署与运营成本。为优化 IPTV CDN系统的配置与性能，用户行为分析是极其重要的一步。

本文利用提出的ASSE模型和SE模型分别对IPTV视频点播用户行为进行回归拟合和对比分析，验证了本文提出的ASSE模型不仅能够更好地拟合出用户视频点播的热度分布，并能够为优化IPTV CDN系统配置、改善视频调度与存储策略提供重要的指导作用。

参考文献：

[1]张旺俊.Web缓存替换策略与预取技术的研究[D].合肥： 中国科学技术大学, 2011.ZHANG W J.Research on Web cache replacement strategy and prefetching technology[D].Hefei： University of Science and Technology of China, 2011.

[2]夏琰.基于实际用户行为分析的缓存研究[D].合肥： 中国科学技术大学, 2011.XIA Y.Research on caching based on actual user behavior analysis[D].Hefei： University of Science and Technology of China, 2011.

[3]韦乐平.三网融合与 IPTV的发展和挑战[J].电信科学,2006, 22(7)：1-5.WEI L P.Triple-play and the development and challenges of IPTV[J].Telecommunications Science, 2006, 22(7)：1-5.

[4]崔华杰.大型直播与点播IPTV系统的用户行为分析[D].广州： 中山大学, 2013.CUI H J.Dissecting user behaviors for a simultaneous live and VOD IPTV system[D].Guangzhou： Sun Yat-sen University,2013.

[5]GUO L, TAN E, CHEN S, et al.The stretched exponential distribution of internet media access patterns[C]//Twenty-Seventh ACM Symposium on Principles of Distributed Computing, PODC 2008, August 18-21, Toronto, Canada.New York：ACM Press, 2008： 283-294.

[6]LAHERRÈRE J, SORNETTE D.Stretched exponential distributions in nature and economy： “fat tails” with characteristic scales[J].The European Physical Journal B - Condensed Matter and Complex Systems, 1998, 2(4)： 525-539.

[7]赵晨阳, 翟少丹.高尔顿与相关理论的产生[J].西北大学学报：自然科学版, 2008, 38(4)：680-684.ZHAO C Y, ZHUO S D.Galton and the invention of correlation[J].Journal of Northwestern University： Natural Science Edition, 2008, 38(4)： 680-684.

[8]李祖亮.基于数学建模的经济变量线性回归统计预测研究[J].中国校外教育, 2011(2)：142-142.LI Z L.Research on statistical prediction of linear regression of economic variables based on mathematical modeling[J].Education for Chinese After-School, 2011(2)：142-142.

[9]贾丹华, 王润润, 王鹏.电信套餐资费预演中客户量的预测方法研究[J].电信科学, 2011, 27(8)： 25-32.JIA D H, WANG R R, WANG P.Research on prediction method of the amount of customers in Telecom services tariff preview[J].Telecommunications Science, 2011, 27(8)： 25-32.

[10]吕游, 刘吉臻, 赵文杰, 等.基于分段曲线拟合的稳态检测方法[J].仪器仪表学报, 2012, 33(1)： 194-200.LV Y, LIU J Z, ZHAO W J, et al.Steady-state detecting method based on piecewise curve fitting [J].Chinese Journal of Scientific Instrument, 2012, 33(1)： 194-200.

[11]方艾, 张玉忠, 徐雄, 等.基于MapR的IPTV用户收视行为分析的方案与实践[J].电信科学, 2017, 33(2)： 138-143.FANG A, ZHANG Y Z, XU X, et al.Scheme and practice of IPTV user viewing behavior analysis based on MapR[J].Telecommunications Science, 2017, 33(2)： 138-143.

[12]王重, 刘黎明.拟合优度检验统计量的设定方法[J].统计与决策, 2010(5)： 154-156.WANG C, LIU L M.Setting method of statistics for goodness of fit[J].Statistics and Decision, 2010(5)： 154-156.