Oil–water pre-separation with a novel axial hydrocyclone☆

Meili Liu,Jiaqing Chen*,Xiaolei Cai,Yanhe Han*,Si Xiong

Department of Environmental Engineering,Beijing Institute of Petrochemical Technology,Beijing 102617,China

1.Introduction

With the large-scale development of deep-sea petroleum resources,the water content of output fluids is ever-increasing so that most of water treatment systems have reached their maximum capacity[1].To overcome this problem,the technology of down hole oil–water separation(DOWS)was proposed utilizing down hole installation of hydrocyclones to pre-separate oil and water,after which the oil was pumped to the surface and the water was re-injected back into the well[2].Hydrocy clones are devices which separate two phases of different densities with the aid of the strong centrifugal force generated by the swirling flow[3–5].Deoiling hydrocyclones used for oily waste water in offshore platforms,are the most common examples of liquid–liquid hydrocyclones[6].However,some disadvantages have been found during the practical application of traditional deoiling hydrocyclone which has tangential inlet for swirl generation[7,8].The vortex flow is easy to swing due to the non-axisymmetric inlet of tangential hydrocyclone[9,10],which brings about oil droplet breakup and high turbulent intensity and then reduces the separation efficiency[11,12].Moreover,the tangential inlet not only leads to large bulk but also consumes high energy.In order to solve the above defects,axial hydrocyclone has been developed[13,14].

Compared to tangential hydrocyclone,axial hydrocyclone has advantages of low-level turbulence,small pressure drop and high handling capacity,which is more feasible for down hole oil–water separation[15–17].The axial hydrocyclone for oil–water separation was first proposed by Dirkz wager[18],which a guide vane was installed in a straight pipe to generate swirling flow.The following studies showed that the separation of oil and water was successfully carried out in the strong swirling flow field generated by the guide vane[19,20].Thereafter,different kinds of axial hydrocy clone were presented and studied[2,21–23].The research results show that axial hydrocyclone with small size,straight-through flow and low pressure drop is an ideal candidate for DOWS application.However,most of studies only present qualitative information and the maximum capacity of the reported axial hydrocyclone is 12 m3·h−1.The handling capacity needs to be further increased.

Ever since the first efficient design of deoiling hydrocyclone proposed by Thew[24],experimental method has been an effective way to investigate the influence of operating parameters or geometry parameters on the separation efficiency[25,26].Recently,in view of the high cost and time consumption of experimental investigation,many attempts have been performed numerically for analysis of oil–water flow through the hydrocyclones.Huang[24]simulated the multiphase flow behavior for the Colman–The whydrocy clone using the Eulerian–Eulerian method,the separation curve of which agreed well with measured ones.Maddahian et al.[27]also used the same approach for the simulation of two-phase flow behavior within two typical designs of hydrocyclones.Results showed that different swirl distributions of two configurations caused differences in velocity and volume fraction.Noroozi et al.[28,29]analyzed the effect of inlet types and inlet chamber body pro files on the separation efficiency of deoiling hydrocyclones by using algebraic slip mixture model.Their simulations showed that the separation efficiency could be improved approximately 8%–10%by a suitabledesign.The Eulerian–Lagrangian approach was applied to study the performance of the de-oiling hydrocyclones as well[8].A complete review of hydrocyclones used for deoiling purpose was summarized by Kharoua[30].Moreover,with the progress of computer technology and numerical analysis theory,several investigations have also been reported for deep understanding of the fundamental fluid mechanics,such as dynamic characteristics[31,32],droplet breakup and coalescence[33–35],G force distribution[36]and rheological behavior[37].The above literature review reveals that numerical simulation has provided another effective tool for investigation of hydrocyclone.

The objective of this study is to present a novel axial hydrocyclone with high handling capacity.The influences of the guide blades,the cone angle of the reducing section as well as the tapered section and the diameter of the over flow pipe on the oil–water separation efficiency are studied using the numerical method.The optimum design of AHC is carried out by using response surface methodology and the feasibility of the optimum AHC is verified by experiments.

2.Novel Hydrocyclone

The AHC consists of four axisym metric sections,which are named cylindrical section,reducing section,tapered section and tail pipe section,as shown in Fig.1.The mixture of oil and water enters into the annular geometry of the cylindrical section,where curved blades used as guide vanes are located,replacing of the tangential inlet used by conventional hydrocyclones.By deflecting it over an angle,the cascade of vanes imposes a tangential velocity on the mixture,establishing a symmetric flow field with a low level of turbulence.Moreover,the built-in vane can reduce the outer dimensions of the apparatus.

The reducing section,which is also an annular space,is designed to achieve higher tangential acceleration by conservation of angular momentum,whilereducing the pressure drop and the shear stress to an acceptable level to avoid droplet breakup.A tube named over flow pipe is mounted on the bottom of the reduction section,via which the reversed flow in the central body exits the hydrocyclone.

The tapered section with lowangle is where most of the separation occurs,because this segment retains high swirl intensity and long residence time.The oil droplets migrate towards the center and form an oil rich core by the action of centrifugal force.Meanwhile,the oil rich core drifts to the over flow pipe under the suction of the adverse pressure gradient in the centerline.

The last part of the design is a long tail pipe with cylindrical cross section.This configuration gives a stable flow for the smallest droplets migrate to the reverse flow while the separated water continues to move upward and is discharged from the under flow out.

3.Numerical Methods

Currently,there are two approaches for the numerical simulation of multiphase flows:the Eulerian–Lagrangian approach and the Eulerian–Eulerian approach.It depends on the concentration of the dispersed phase in the continuous phase using which approach to perform multiphase simulations.The Eulerian–Lagrangian approach models primary and dispersed phase separately.A low volume fraction usually less than 10%is appropriate for this approach[24,30,32].Therefore,the model is unsuitable for liquid–liquid hydrocyclones in the current case.The Eulerian–Eulerian approach is an alternate of the Lagrangian approach and indispensable when simulation with high loading(more than 10%)of dispersed phase is desired.This approach treats the different phases as in terpenetrating continua and can completely capture the multiphase nature of flows in deoiling hydrocyclones by solving conservation equations for each phase[24,30].A full Eulerian approach is used in this paper,which permits simulating the effects of turbulence on dispersed phase and the interaction of dispersed phase with primary phase.

3.1.Governing equations

Water is considered as continuous phase,while oil droplets are considered as dispersed phase.For each phase,the model consists of continuity,momentum and turbulence equations.The continuity and momentum equation is expressed as Eqs.(1)and(2).

where k denotes water(w)or oil(o),α refers to the volume fraction(αw+αo=1),ρ is the density,is the velocity,is the acceleration due to gravity andis the k th phase stress–strain tensor which is calculated by Eq.(3).

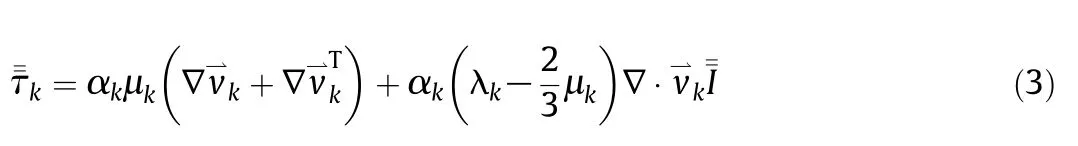
Here μkand λkare the shear and bulk viscosity of phase k.The term ofin Eq.(2)represents the interaction between dispersed and continuous phase,including the drag force,the lift force and the virtual mass force.In this work,the lift force is discounted because of the small diameter of droplets and the virtual mass force is also ignored due to the lowdensity differences between the two liquids.Therefore,only the drag force is considered in the interphase momentum exchange term via Eq.(4):

where dois droplet diameter and CDis drag coefficient.

Fig.1.Dimensions and parameters of the hydrocyclone.

3.2.Turbulence model

The turbulence closure model is a key component in the description of the fluid dynamics of the hydrocyclone.Previous numerical simulations show applicability of Reynolds stress model(RSM)for swirling flow in hydrocyclones,which can predict anisotropic turbulence and capture fluctuations of highly swirling flow bounded by curved surface[38,39].ALarge Eddy Simulations(LES)also provides good prediction of turbulence encountered in hydrocyclones[31,40],however,it requires much higher computational resources when compared with RSM.So RSM model has been used for simulations of the momentum transport induced by turbulence.

3.3.Geometry and mesh generation

AHC with a capacity of 30 m3·h−1is adopted in the simulation,and its geometry size is given in Table 1.In order to keep consistent with actual operation process,the hydrocyclone is located in acylindrical vessel with a diameter of 200 mm,as shown in Fig.2.Four non-uniform structured hexahedron grids are used for three-dimensional simulations in order to take into account of mesh in dependency.A mesh refinement is done in the region with high gradient of phase volume fraction and velocity,such as areas near the wall and the central core.Fig.2 shows the generated mesh.A cylindrical coordinate is used in the simulation and the origin of the coordinate is set at the bottom end of reducing section.

Table 1 Geometrical dimensions of AHC(mm)

3.4.Boundary conditions

The inlet of the cylindrical vessel is defined as velocity inlet,where the velocity magnitude is calculated according to the in flow-rates and the oil volume fraction is set to be 15%.The density and viscosity of the oil are set to be 890 kg·m−3and 0.00332 Pa·s,respectively.The mean diameter of oil is 60 μm.The hydraulic diameter method is used for specification of turbulence at in flow boundaries.The outlet flow is assumed to be fully developed,and the mass flow rate is given by specifying the flow rate weighting.The walls are regarded as the no-slip boundary conditions,where the standard wall function is applied to determine the flow near walls.

3.5.Solution methodology

The governing equations mentioned in the section of Governing Equations are discretized with the QUICK scheme and solved by using the commercial CFD code FLUENT 15.0.The coupling between velocity and pressure is dealt with the phase-coupled SIMPLE algorithm.The solution is considered to be converged when the scaled residual of the continuity is below1×10−4.

4.Results and Discussions

4.1.Grid dependence

Fig.3 shows the tangential and the axial velocity at a location of the tapered section.It is evident that the velocity pro files obtained by different meshes are mostly overlapping with each other when the grid number exceeds 238065.To ensure the reliability,the mesh density of 423525 is chosen for the subsequent study.

4.2.Flow characteristics

Fig.4 shows the velocity contours for a longitudinal section and the velocity vectors for different cross sections.As can be found from Fig.4,the flow in the outer cylindrical vessel is close to a plug- flow and the velocity magnitude is relatively small.When the flow moves through the cylindrical section,the fluid gains a rotating momentum under the action of guide vanes,resulting in a little increase of the velocity magnitude.As the flow moves into the reducing section,in order to remain the same angular momentum,a gradual increase of the rotating velocity is observable.The above rotating flow generates a double swirling flow in the tapered section.The outer flow near the wall spirals to the tail pipe with a large diameter,whereas the inner flow spirals towards the over flow pipe with a relatively small diameter.The rotation intensity decays along with the fluid moves into the tail pipe.Obviously,the designed axial hydro cyclone produces a symmetry swirling flow being suitable for oil–water separation[8,18,28].

Fig.2.The schematic diagram of the mesh topology.

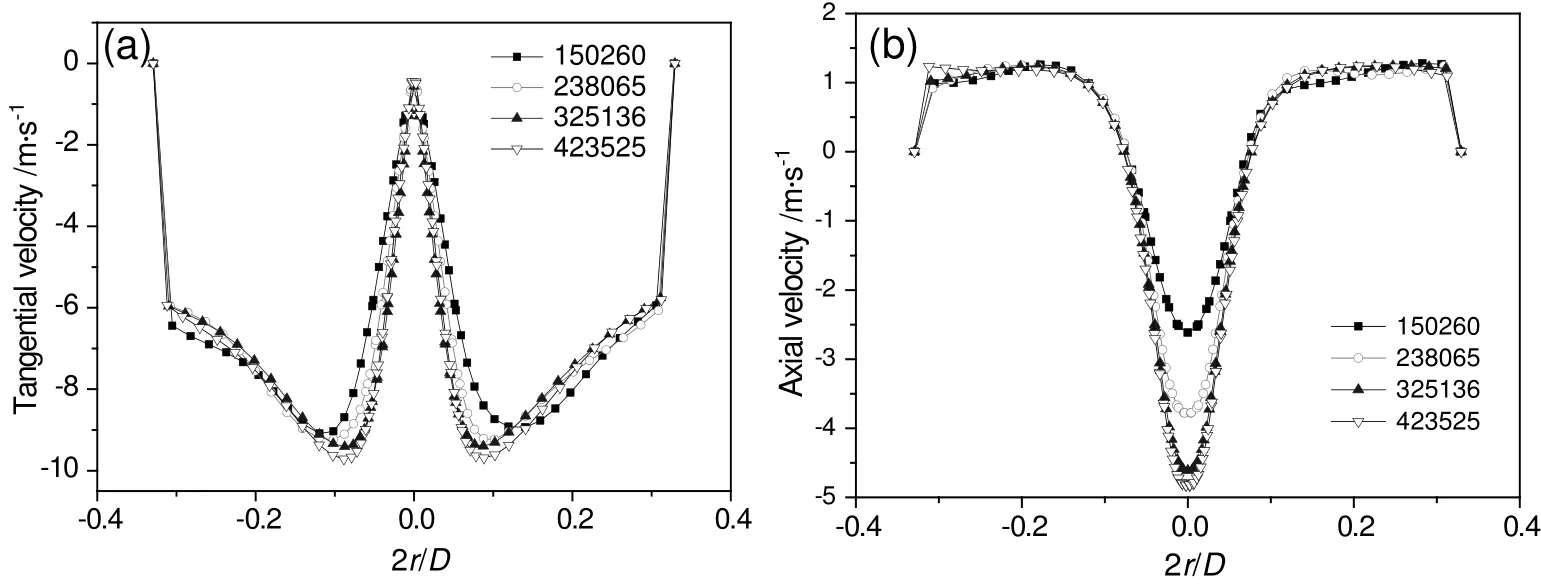
Fig.3.Comparison of(a)tangential and(b)axial velocity simulated with different grids.

Fig.4.Velocity contours in longitudinal section and velocity vectors in different cross sections.

Fig.5 shows the variation of oil concentration over time,that is,the formation of the oil core.In the early stage,the amount of fluid flows into AHC is so small that the swirl intensity is too low to be effective,as seen in Fig.5(a)and(b).As the time progresses,the gradual stability of the rotating flow makes the oil concentrate towards the axis,forming an oil core near the over flow pipe,as shown in Fig.5(c),(d)and(e).When the double swirling flow goes steady,the oil–water separation in the tapered section becomes predominant,bringing about a stable oil core with highly concentrated oil in the AHC center,as shown in Fig.5(f).The above condition certifies the feasibility of the AHC design.

4.3.Influence of structure parameters

A large of research shows that the oil–water separating process is influenced significantly by the separator structure[28,29,31].Therefore,cylindrical section,reducing section,tapered section and over flow pipe are investigated in the following work.The separation efficiency is calculated by Eq.(5):

where˙morepresents mass flow rate of oil in the over flow and˙minrepresents mass flow rate of oil in the in flow.

4.3.1.Effect of cylindrical section

Fig.5.Variation of oil concentration over time.

Fig.6.Effect on the AHC performance of cylindrical section(a)with different blade heights and(b)with different blade deflecting angles.

The effect of cylindrical section on the AHC performance is largely caused by the blades located in cylindrical section.Therefore,the influence of the blade structure on the separation performance is investigated,as shown in Fig.6.With the blade height increase,the flow area increases,resulting in a decrease of flow velocity and available rotational energy.It is well known that the high rotating velocity is conducive to oil–water separation whilst inducing high-energy consumption.So the separation efficiency and the pressure drop decrease as the blade height increases,as shown in Fig.6(a).This indicates that the diminution of blade height can effectively improve the separation efficiency.However,a small flow area induces huge energy consumption.Therefore,the blade height should be controlled in a reasonable range.Fig.6(b)shows that the separation efficiency raises with the increase of blade deflecting angle.That because the rotating velocity can be enlarged by increasing blade deflecting angle.Meanwhile,the pressure drop increases due to the energy consumption caused by the change of the flow direction.Even more importantly,droplet breakup is likely to occur if the rotation intensity is large enough.So,the blade deflecting angle should also be controlled in a reasonable range.

4.3.2.Effect of reducing section

Fig.7 shows the effect of reducing section on the AHC performance.Variation of the coneangle α has only influence on the rate of change in the flow field but not on the final distribution of the velocity in the tapered section.However,a larger cone angle brings lower turbulence intensity in the vortex.Therefore,the separation efficiency and the pressure drop increase slightly when the cone angle rises from 10°to 30°,as shown in Fig.7.

4.3.3.Effect of tapered section

The flow with high swirl intensity in tapered section is the main role for oil–water separation.Researches indicate smaller tapered angle equate to better performance[31,41,42].Hence,the tapered angle is controlled to be less than 10°.Fig.8 shows the effect of tapered section on the AHC performance.The separation efficiency decreases with the increasing tapered angle.As revealed in researches,the smaller the tapered angle is,the longer the residence time is,resulting in enhanced oil–water separation.Meanwhile,the pressure drop increases with the increasing tapered angle.Hence,small tapered angle is recommend in the case of footprint allows.

4.3.4.Effect of over flow pipe

In order to keep smooth discharge of concentrated oil,the results of orthogonal test show that the diameter of over flow pipe should be controlled at least 20 mm.Fig.9 shows the effect of over flow pipe on the AHC performance.The separation efficiency increases regularly with over flow pipe diameter increasing from 20 to 26 mm,and then decreases abruptly when the over flow pipe diameter rises from 26 to 28 mm.This indicates that a low velocity of oil discharge is not allowed due to its weak suction effect on the inner oil core.

4.4.Optimum structural design

On the basis of above single factor experiments,response surface methodology is employed to investigate the interaction effect and to obtain optimum matching relations between structures,the results of which are shown in Fig.10.The tapered section has strongest interaction with the reducing section and has moderate interaction with the cylindrical section.In accordance with results of single factor,large tapered angle with the combination of small cone angle is the last choice.However,smallest tapered angle with largest coneangle cannot acquire the highest efficiency,as shown in Fig.10(a)and(b).It can be seen from Fig.10(b)and(c)that large blade deflecting angle combined with small tapered angle and moderate cone angle will gain high separation efficiency.Optimum structure parameters are obtained on the base of results of response surface methodology.

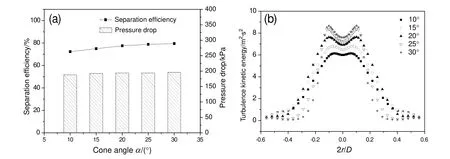
Fig.7.Effect of reducing section on(a)separation performance and(b)turbulence intensity at the bottom of reducing section.

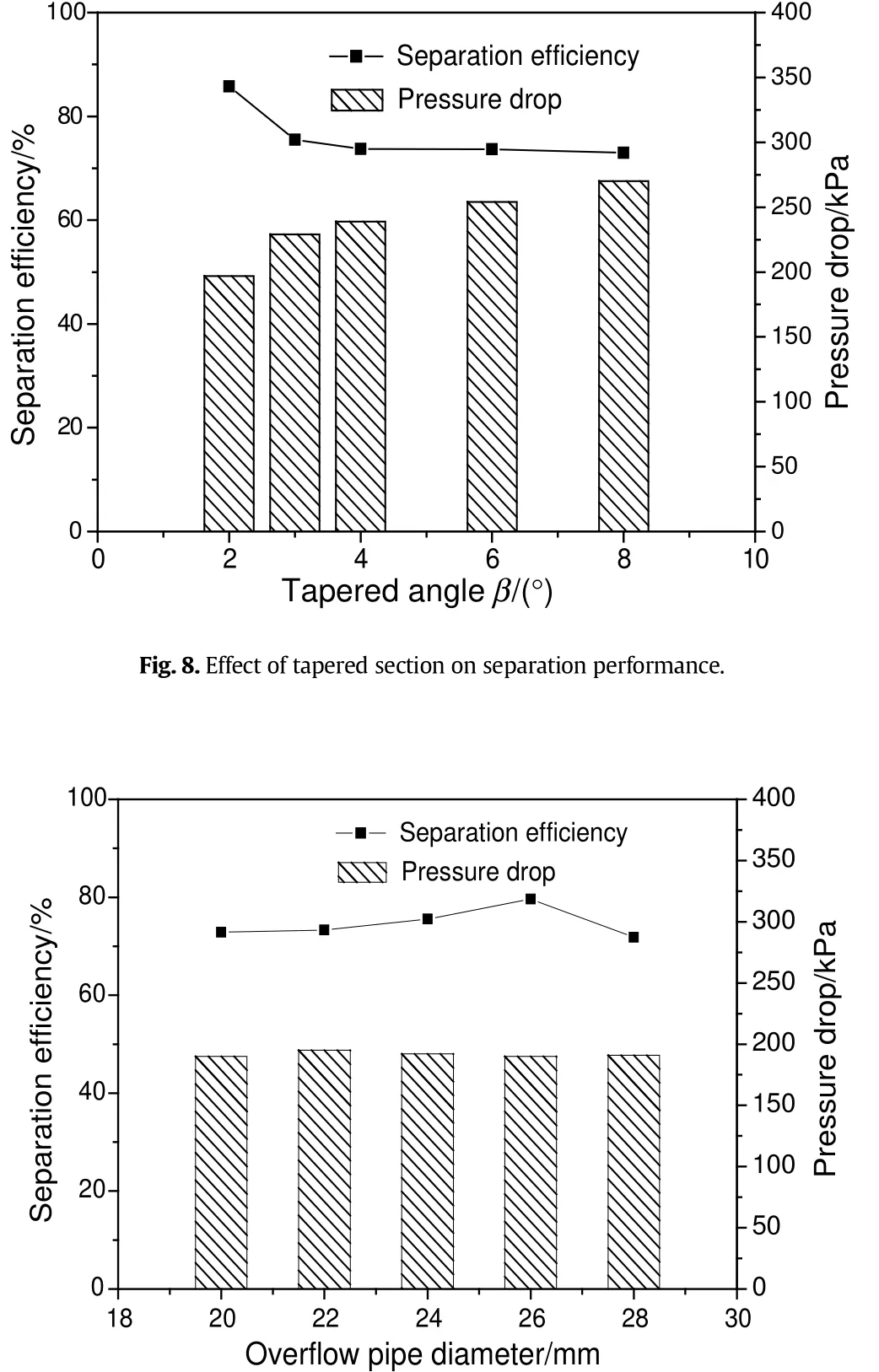
Fig.9.Effect of over flow pipe on separation performance.

Fig.10.Response surface of separation efficiency on different factors.

Fig.11.Comparison of separation efficiency between experiment and simulation.

4.5.Performance validation by laboratory experiment

In order to validate the feasibility of the AHC design,an experimental device with the capacity of 1 m3·h−1is set up according to the principle of similitude.Due to the restriction in university labs,the maximum oil volume fraction at the AHC inlet is10%.The numerical and experimental results of the AHC are shown in Fig.11.The separation efficiency increases with the increasing split ratio as well as the increasing inlet volume fraction.Simulation results agree well with experimental data,the maximum deviation of which is 3.3%.Therefore,the comparison results shown in Fig.11 indicate excellent performance of the designed AHC as well as reliability of the simulation method.

5.Conclusions

Numerous oil fields are encountering the problem of high water content.In order to overcome the above problem,an axial hydro cyclone with the capacity of 30 m3·h−1is proposed to separate water from crudeoil.The effect of structure parameters on the oil–water separation is discussed by using CFD methods.Narrowing the blade height and increasing the blade deflecting angle will effectively increase the rotating velocity in hydrocy clone.Therefore,increasing the blade deflecting angle and reducing the blade height can significantly enhance the oil–water separation efficiency.Small tapered angle will keep oil droplets in separation space for a long time,so separation efficiency increases with the decreasing tapered angle.Relatively,reducing section and over flow pipe have less influence on the oil–water separation.However,the strong interaction between reducing section and tapered section cannot be ignored in AHC design.An optimum design of AHC is obtained by using response surface methodology.Laboratory experiments exhibit that the designed AHC has an excellent performance for oil–water separation.

[1]B.E.Bowers,R.F.Brownlee,P.J.Schrenkel,Development of a down hole oil/water separation and reinjection system for offshore application,SPE J.15(2000)115–122.

[2]S.Y.Shi,J.Y.Xu,Flow field of continuous phase in a vane-type pipe oil-water separator,Exp.Thermal Fluid Sci.60(2015)208–212.

[3]B.Wang,K.W.Chu,A.B.Yu,Numerical study of particle- fluid flowin a hydrocyclone,Ind.Eng.Chem.Res.46(2007)4695–4705.

[4]H.L.Wang,Y.H.Zhang,J.G.Wang,H.L.Liu,Cyclonic separation technology:Researches and developments,Chin.J.Chem.Eng.20(2012)212–219.

[5]R.A.Johnson,W.E.Gibson,D.R.Libby,Performance of liquid–liquid cyclones,Ind.Eng.Chem.Fundam.15(1976)110–115.

[6]A.Belaidi,M.T.Thew,S.J.Munaweera,Hydrocyclone performance with complex oil–water emulsions in the feed,Can.J.Chem.Eng.81(2010)1159–1170.

[7]Z.S.Bai,H.L.Wang,S.T.Tu,Oil–water separation using hydrocyclones enhanced by air bubbles,Chem.Eng.Res.Des.89(2011)55–59.

[8]M.Nascimento,I.Bicalho,J.Mognon,C.Ataide,C.Duarte,Performance of a new geometry of deoiling hydrocyclones:Experiments and numerical simulations,Chem.Eng.Technol.36(2013)98–108.

[9]J.G.Wang,Z.S.Bai,Q.Yang,Y.Fan,H.L.Wang,Investigation of the simultaneous volumetric 3-component flow field inside a hydrocyclone,Sep.Purif.Technol.163(2016)120–127.

[10]Y.F.Chang,A.C.Hoffmann,A Lagrangian study of liquid flow in a reverse- flowhydrocyclone using positron emission particle tracking,Exp.Fluids 56(2015)1–14.

[11]L.Wang,J.Feng,X.Gao,X.Peng,Investigation on the oil–gas separation efficiency considering oil droplets breakup and collision in a swirling flow,Chem.Eng.Res.Des.117(2017)394–400.

[12]P.Qian,J.Ma,Y.Liu,X.J.Yang,Y.H.Zhang,H.L.Wang,Concentration distribution of droplets in a liquid–liquid hydrocyclone and its application,Chem.Eng.Technol.39(2016)953–959.

[13]S.Amini,D.Mowla,M.Golkar,F.Esmaeilzadeh,Mathematical modelling of a hydrocyclone for the down-hole oil–water separation(DOWS),Chem.Eng.Res.Des.90(2012)2186–2195.

[14]Y.Zhang,M.H.Jiang,Numerical simulation of multi-grade separators for multiphase fluid med ia d own hole in offshore oil field,International Conference on Ocean,Offshore and Arctic Engineering,Shanghai,China,2010.

[15]A.D.Rocha,A.C.Bannwart,M.M.Ganzarolli,Numerical and experimental study of an axially induced swirling pipe flow,Int.J.Heat Fluid Flow53(2015)81–90.

[16]Z.B.Wang,Y.Ma,Y.H.Jin,Simulation and experiment of flow field in axial- flowhydrocyclone,Chem.Eng.Res.Des.89(2011)603–610.

[17]S.Y.Shi,J.Y.Xu,H.Q.Sun,J.Zhang,D.H.Li,Y.X.Wu,Experimental study of a vanetype pipe separator for oil–water separation,Chem.Eng.Res.Des.90(2012)1652–1659.

[18]M.Dirkzwager,A newaxial cyclone design for fluid- fluid separation,Ph D Thesis,Delft University of Technology,Delft,1996.

[19]S.Murphy,R.Delfos,M.J.B.M.Pourquié,Ž.Olujić,P.J.Jansens,F.T.M.Nieuwstadt,Prediction of strongly swirling flow within an axial hydrocyclone using two commercial CFD codes,Chem.Eng.Sci.62(2007)1619–1635.

[20]L.van Campen,R.F.Mudde,J.Slot,H.Hoeijmakers,A numerical and experimental survey of a liquid–liquid axial cyclone,Int.J.Chem.React.Eng.10(2012)1205–1224.

[21]Y.Ma,Z.B.Wang,Y.H.Jin,Droplet coalescence and breakup and its influence factors in vane-guided hydrocyclone,CIESC J.62(2011)420–426(in Chinese).

[22]L.J.A.M.Van Campen,Bulk dynamics of droplets in liquid-liquid axial cyclones,Ph D Thesis,Delft University of Technology,Delft,2014.

[23]Y.Zhang,Y.Wang,L.X.Zhao,F.Li,F.S.Wang,G.X.Zheng,Design of hydrocyclone with axial inlet and its performance used in well bore,International Conference on Ocean,Offshore and Arctic Engineering,San Francisco,USA,2014.

[24]S.Huang,Numerical simulation of oil-water hydrocyclone using Reynolds-stress model for Eulerian multiphase flows,Can.J.Chem.Eng.83(2005)829–834.

[25]T.Husveg,O.Rambeau,T.Drengstig,T.Bilstad,Performance of a deoiling hydrocyclone during variable flow rates,Miner.Eng.20(2007)368–379.

[26]N.Y.Zhou,Y.X.Gao,W.An,M.Yang,Investigation of velocity field and oil distribution in an oil-water hydrocyclone using a particle dynamics analyzer,Chem.Eng.J.157(2010)73–79.

[27]R.Maddahian,M.Asadi,B.Farhanieh,Numerical investigation of the velocity field and separation efficiency of deoiling hydrocyclones,Pet.Sci.9(2012)511–520.

[28]S.Noroozi,S.H.Hashemabadi,CFD simulation of inlet design effect on deoiling hydrocyclone separation efficiency,Chem.Eng.Technol.32(2009)1885–1893.

[29]S.Noroozi,S.H.Hashemabadi,CFD analysis of inlet chamber body pro file effects on de-oiling hydrocyclone efficiency,Chem.Eng.Res.Des.89(2011)968–977.

[30]N.Kharoua,L.Khezzar,Z.Nemouchi,Hydrocyclones for de-oiling applications-a review,Pet.Sci.Technol.28(2010)738–755.

[31]M.Saidi,R.Maddahian,B.Farhanieh,Numerical investigation of cone angle effect on the flow field and separation efficiency of deoiling hydrocyclones,Heat Mass Transf.49(2013)247–260.

[32]M.Saidi,R.Maddahian,B.Farhanieh,H.Afshin,Modeling of flowfield and separation efficiency of a deoiling hydrocyclone using large eddy simulation,Int.J.Miner.Process.112(2012)84–93.

[33]S.Amini,D.Mowla,M.Golkar,Developing a newapproach for evaluating a de-oiling hydrocyclone efficiency,Desalination 285(2012)131–137.

[34]S.Schutz,G.Gorbach,M.Piesche,Modeling fluid behavior and droplet interactions during liquid-liquid separation in hydrocyclones,Chem.Eng.Sci.64(2009)3935–3952.

[35]S.Noroozi,S.H.Hashemabadi,A.Chamkha,Numerical analysis of drops coalescence and breakage effects on de-oiling hydrocyclone performance,Sep.Sci.Technol.48(2013)991–1002.

[36]C.Banerjee,K.Chaudhury,A.K.Majumder,S.Chakraborty,Swirling flow hydrodynamics in hydrocyclone,Ind.Eng.Chem.Res.54(2015)522–528.

[37]C.J.Li,Q.Huang,Rheology-based computational fluid dynamics modeling for deoiling Hydrocyclone efficiency,Chem.Eng.Technol.39(2016)899–908.

[38]A.M.Jawarneh,G.H.Vatistas,A.M.Jawarneh,G.H.Vatistas,Reynolds stress model in the prediction of confined turbulent swirling flows,J.Fluids Eng.128(2006)1377–1382.

[39]M.Ghadirian,R.E.Hayes,J.Mmbaga,A.Afacan,Z.Xu,On the simulation of hydrocyclones using CFD,Can.J.Chem.Eng.91(2013)950–958.

[40]J.A.Delgadillo,R.K.Rajamani,Large-Eddy simulation(LES)of large Hydrocyclones,Part.Sci.Technol.25(2007)227–245.

[41]R.Delfos,S.Murphy,D.Stanbridge,Ž.Olujić,P.J.Jansens,A design tool for optimising axial liquid–liquid hydrocyclones,Miner.Eng.17(2004)721–731.

[42]L.G.M.Vieira,B.C.Silvério,J.J.R.Damasceno,M.A.S.Barrozo,Performance of hydrocyclones with different geometries,Can.J.Chem.Eng.89(2011)655–662.