多缝型锥管布浆器的探索性研究

侯顺利 卫 魏

(陕西科技大学机电工程学院，陕西省造纸技术及特种纸品开发重点实验室，陕西西安，710021)

流浆箱是纸机的心脏，而布浆器是流浆箱的重要部件之一，是将净化后的浆料均匀分布和流送到流浆箱内的装置[1]。现代纸机的流浆箱多采用方锥管布浆器，由进浆总管、布浆阻流元件及回流装置组成。常用的布浆阻流元件有支管、孔板、阶梯扩散管等。而现在普遍使用的支管或孔板，不能调节局部浆流流量。有专利[2]提出了一种可以旋转调节的多缝型布浆阻流元件，本研究将针对这种多缝型布浆阻流元件，进行前期研究，主要研究它的布浆均匀性，为在线调节性能研究提供理论基础。

1 多缝型锥管布浆器

图1为多缝型锥管布浆器结构原理图。如图1所示，多缝型锥管布浆器主要由锥形总管、阻流元件及回流端组成。浆料从锥形总管大端进入锥管内部，在横向流动的过程中，由于各阻流元件之间的缝隙使纸浆在纵向形成多个支流，然后进入堰池。缝的结构形状和尺寸至关重要，它不仅影响浆流加速比，还对布浆效果有重大影响。本研究初步将缝设计成一种狭长的窄缝结构，并对缝结构进行初步优化。

图1 多缝型锥管布浆器结构原理图

2 多缝型锥管布浆器内数值模拟

本研究采用ANSYS-FLUENT对布浆器内流体进行数值模拟，研究布浆总管回流量和缝长对浆流均匀分布的影响，并对布浆器结构进行优化[3]。

2.1 数学模型

此次设计在计算中用到的主要方程有：

N-S方程：

2.2 湍流模型

湍流模型计算选用标准的k-ε模型，此模型优点是适用范围广、经济且有合理的精度，满足此次设计的需要。

2.3边界条件

计算区域的入口采用质量流量入口边界条件，各缝出口采用压力出口条件，近壁区采用标准壁面函数进行处理。

2.4 模拟参数的确定与建模

首先通过UG进行三维建模(计算模型包括入口过渡管、进浆总管、布浆多缝等布浆器主要部分)，然后导入ICEM CFD中进行网格划分，随后将网格导入FLUENT中进行模拟。本次模拟针对拟建设的实验装置，流浆箱的唇口宽度w=1800 mm，唇口喷浆速度为600 m/min，喷浆量为108 kg/s。锥形总管入口端浆流流速为2 m/s，回流量按进口流量的10%计算，则总流量为120 kg/s；按照常规布浆器的设计计算，确定该布浆器宽度W为200 mm，入口高度H0为300 mm。

考虑到将来需要加设稀释水控制装置，将缝间距初步确定为58 mm，共需31排缝，排成一列。根据文献[4]，支管内浆流速度与总管内浆流速度比应大于2.5，将多缝内浆流速度与总管内浆流速度的加速比取为3。为了保证多缝内浆流不发生堵塞，同时考虑到加速比，初步将缝宽度确定为12 mm，计算得缝高度为50 mm，初步拟定缝长度为150 mm。为了防止多缝出口处发生大的横向流动和涡旋，在缝的下游增加一段扩散管。

按照Baines公式采用多段折线法[5- 6]，取N=10(N代表布浆器分段数)。锥形总管截面的设计值如表1所示。其中，Ln代表布浆器分段长度，An代表布浆器分段长度下总管截面积，W代表布浆器宽度，Hn代表布浆器分段长度下总管截面高度，An/AO代表总管截面比。将布浆多缝沿进浆总管进浆方向依次命名为outlet1，outlet2，outlet3，…，outlet31。进入锥管的浆料浓度一般在1%左右，湍流状态下其特性与水较为接近。因此，对布浆器内浆流的分析可按照水力学流体力学进行[7]，在模拟过程中，用水代替纸浆悬浮液，所建多缝型锥管布浆器模型如图2所示。为了便于比较，按相同的参数建立了支管型锥管布浆器模型，如图3所示。

3 数值模拟结果与分析

3.1 出口流量的数值模拟

图4表示多缝型锥管布浆器和支管型锥管布浆器的流量分布情况模拟结果。从图4可以看出，在相同的条件下，支管型锥管布浆器的流量分布偏差为-1.84%～2.41%，即最大误差为4.25%；多缝型锥管布浆器的偏差为-1.35%～2.0%，即最大误差为3.35%。说明在相同的条件下多缝型锥管布浆器的流量分布比支管型锥管布浆器的流量分布更加均匀。另外从图4可看出，锥形总管内压力沿浆料流动方向呈波浪式波动，因此按拜纳斯公式以10%回流量计算得到的等压锥管布浆器流量分布误差较大，还需要进一步优化。

表1 锥形总管截面设计值

图2 多缝型锥管布浆器模型

图3 支管型锥管布浆器模型

图4 多缝型锥管布浆器和支管型锥管布浆器的流量分布对比图

3.2 不同回流量下多缝型锥管布浆器的数值模拟

图5和图6分别为在减小和增大回流量的条件下，多缝型锥管布浆器总管中各排缝的流量，模拟过程中保持各缝的总流量都为108 kg/s，即各排缝的平均流量为3.484 kg/s，回流量大小通过调节总管的入口流量和回流端流量得到，回流量分别为0、2.5%、5%、7.5%、10%和10%、12.5%、15%、17.5%、20%。

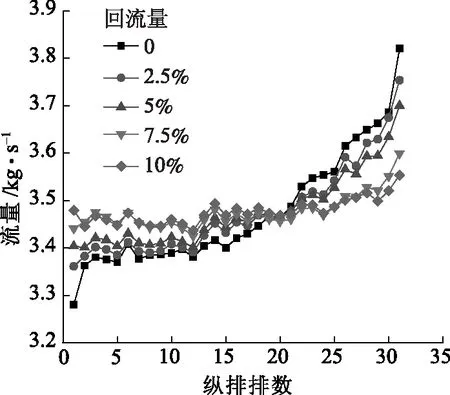
图5 减少总管回流量对缝流量的影响

从图5可看出，当减小总管回流量时，各排缝流量分布形式大体相同，但靠近进口端的缝流量减小，而靠近回流端缝的流量增大。

从图6可看出，当增大总管回流量时，各排缝流量分布形式大体相同，但靠近进口端的缝流量增大，而靠近回流端缝的流量减小。

图6 增大总管回流量对缝流量的影响

图7 回流量对缝流量最大值和最小值的影响

图7为回流量对缝流量最大值和最小值的影响。从图7看出，回流量以10%为基准，当减小回流量时，缝流量的最大值持续增大，而最小值持续减小；当增大回流量时，缝流量的最大值先降低后升高，而缝流量的最小值持续降低；当回流量为12.5%时，缝流量的最大值与最小值之间的差值最小，说明当回流量为12.5% 时，布浆效果最好。按拜纳斯公式以10%回流量计算得到的多缝型锥管布浆器流量分布误差还较大，而实际回流量为12.5%时，布浆效果最好。

3.3 不同缝长锥管布浆器的数值模拟

保持各缝的总流量都为108 kg/s，回流量为10%，即各排缝的平均流量为3.484 kg/s，基于图2的模型，缝长分别为100、125、150、175、185和200 mm对布浆器进行数值模拟，其模拟结果如图8所示。从图8可以看出，各缝流量的基本趋势大体相同，但长度为100 mm 和200 mm的各排缝中，流量波动较大，反应总管内的压力不稳定，所以缝长不宜过长或过短。

图8 不同缝长下各排缝流量

图9为缝长对缝流量最大值和最小值的影响。从图9可看出，缝长以150 mm为基准，当减小缝长时，缝流量的最大值先降低后升高，而最小值持续降低；当增大缝长时，缝流量的最大值先降低后升高，而最小值先降低后升高再降低；但当缝长为185 mm时，最大值与最小值都更接近于平均值，说明当回流量不变时，缝长为185 mm时，多缝型锥管布浆器的布浆效果最好。这可能是由于浆流从总管转折流向多缝时，在一段距离内呈加速状态，导致多缝内出流部分收缩，出现孔口效应，这种大角度的转向流动，不仅带来了较大的分岔损失，而且在多缝入口处产生了涡流区，引起了多缝内下游较大范围的压力波动，出现了不稳定的流动，影响范围不小于6倍支管直径[8]。但当缝长大于185 mm以后，多缝流量偏差反而增大，这可能是缝下游浆流的扩散作用引起的，因此在设计缝长时，缝长不宜过长或过短，并不小于8倍缝的水力直径。

图9 缝长对缝流量最大值和最小值的影响

图10 优化后多缝型锥管布浆器模型结构

3.4 布浆器的优化

从上面的数值模拟结果分析可知，浆料沿流动方向压力有一定波动，且在总管两端压力波动幅度较大，从而导致整体多缝流量的误差加大，所以针对此问题， 考虑到浆流从锥形总管进入多缝时，速度发生急剧变化，会产生不稳定的二次流或发生流体与管壁分离的现象，同时为了减少挂浆，对布浆器结构进行了优化[9- 10]。即在布浆器的锥形总管与多缝的连接处加入半径分别为2.5、5、7.5、10、12.5以及15 mm的圆弧，如图10所示。图10(b)为局部放大图。研究发现，圆弧半径大于12.5 mm和小于2.5 mm时，在多缝入口处将会产生较大的压力扰动，影响下游的浆流分布，使布浆效果变差，而当圆弧半径为7.5 mm时，压力扰动减为最弱，其流量误差减小到-0.63%～0.89%，模拟结果如图11所示。优化前后缝入口处的湍流强度云图和速度流线图分别如图12和图13所示。

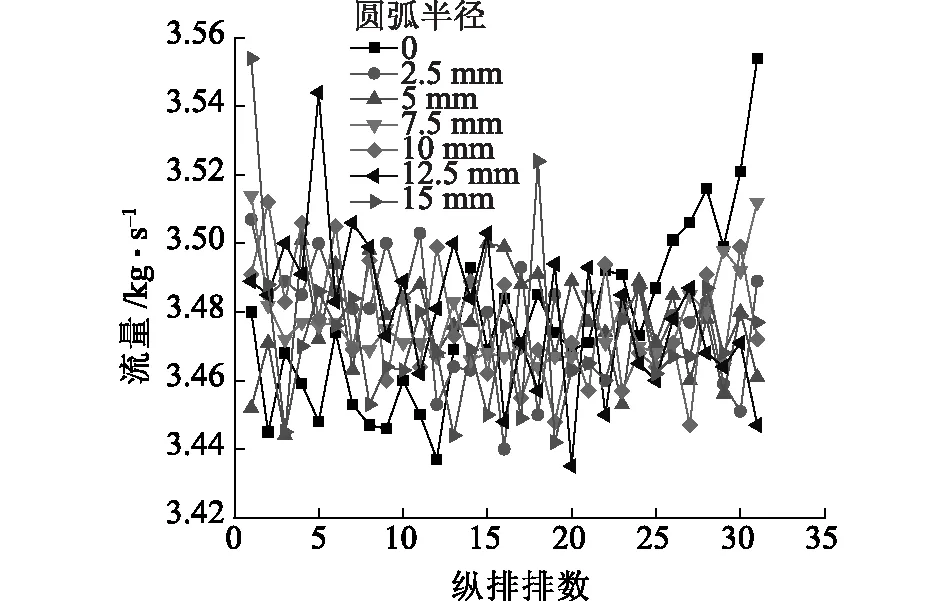
图11 不同圆弧半径下各排缝流量

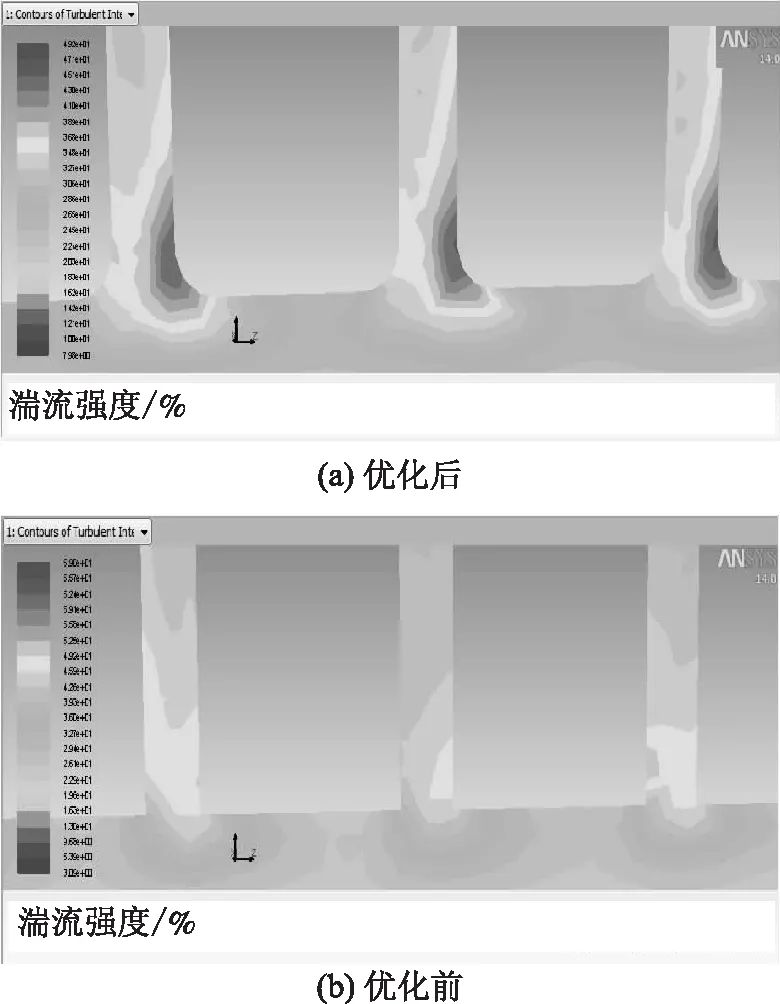
图12 优化前后多缝入口处湍流强度云图

从图12入口湍流强度云图可以看出，优化后多缝入口处湍流强度显著提高，更有利于分散纤维，并防止入口处浆流发生堵塞。

从图13入口速度流线图中可以看出，优化后，在多缝入口处对浆料流动的导向性更好，缝内速差加大，剪切作用更强，更有利于分散纤维。

同时对缝出口的3种扩散管形状(直扩型、阶梯型、圆弧型)进行了对比研究，其模拟结果如图14所示。结果发现，圆弧型扩散管对布浆均匀性更有利，其圆弧半径为265 mm，扩散管长度为90 mm。

优化前后多缝出口处的湍流强度云图和速度流线图分别如图15和图16所示。

从图15多缝出口处湍流强度云图可以看出，优化后多缝出口处湍流强度显著提高并且更加均匀，从而有利于分散纤维。

图13 优化前后多缝入口处的速度流线图

图14 3种扩散管对缝出口流量的影响

图15 优化前后多缝出口处湍流强度云图

从图16多缝出口处速度流线图中可以看出，优化后多缝出口速度分布更加均匀，这样更有利于浆料在混合室中快速混合均匀。

图16 优化前后多缝出口处的速度流线图

图17表示多缝型锥管布浆器优化前后的流量分布情况。

从图17可以看出，优化后：①各缝流量与平均值(3.484 kg/s)的偏差由-1.35%～2.0%变为-0.57%～0.86%，最大误差为1.43%，相对于优化前有了显著降低，减小了流量的偏差范围，使布浆均匀性提高；②除第1排缝的流量偏差有所增大外，其余第2～31排缝的流量更接近于平均值，尤其是第31排缝的流量由3.554 kg/s降为3.512 kg/s，与平均值的偏差降低了1.2%。由此可知，优化后的多缝型锥管布浆器完全可以满足一般纸机的布浆要求，而且布浆均匀性优于支管型锥管布浆器。

图17 多缝型锥管布浆器优化前后流量的数值模拟结果

4 结论与展望

本研究通过采用ANSYS-FLUENT对多缝型锥管布浆器内流体进行数值模拟，研究布浆总管回流量和缝长对浆流均匀分布的影响，并对多缝型锥管布浆器结构进行优化。

4.1相同条件下多缝型锥管布浆器的流量分布比支管型锥管布浆器更加均匀，最大误差缩小了0.9%。

4.2按拜纳斯公式以10%回流量计算得到的等压锥管布浆器流量分布误差较大，而实际回流量为12.5%时，布浆效果最好。

4.3优化后缝长为185 mm，多缝入口圆弧半径为7.5 mm，出口圆弧半径为265 mm，扩散管长度为90 mm时，各缝流量最大误差为1.43%，可满足一般纸机的布浆要求。

多缝型锥管布浆器从结构原理上可以实现在线调节缝宽，以进一步减小布浆流量分布误差，并减小或取消回流量。本次对多缝型锥管布浆器的初步研究，对于今后研究多缝型布浆器在线调节性能具有重要意义。

参 考 文 献

[1] Yang Hai-yan, Hou Shun-li, Niu Xu-zhong. Research on Control of Dilution Water Hydraulic Headbox[J].Paper and Paper Making, 2013, 32(4): 4.

杨海燕, 侯顺利, 牛绪中. 稀释水水力式流浆箱的控制探索[J].纸和造纸, 2013, 32(4): 4.

[2] Hou Shun-li, Wei Wei. Adjustable cone-shaped non-reflow mortar, China: CN 105839444 A[P].2016- 09- 23.

侯顺利, 卫 魏. 免回流可调锥形布浆器, 中国: CN 105839444 A[P].2016- 09- 23.

[3] Liu Wei, Chen Ke-fu, Li Jun. Numerical simulation of flow characteristics in a square pipe beater[J].Journal of South China University of Technology: Natural Science Edition, 2011, 39(3): 13.

刘 伟, 陈克复, 李 军. 方锥管布浆器内流动特性的数值模拟[J].华南理工大学学报: 自然科学版, 2011, 39(3): 13.

[4] Kang Guo-bing. Key technology and mechanism of hydraulic headbox and CFD application[D]. Guangzhou: South China University of Technology, 2011.

康国兵. 水力式流浆箱关键技术机理研究与CFD应用[D].广州: 华南理工大学, 2011.

[5] Hou Shun-li, Yang Hai-yan. Simulation Analysis and Structure Optimization of Tapered Pipe Fabricator[J].Paper and Paper Making, 2013, 32(11): 17.

侯顺利, 杨海燕. 锥管布浆器的模拟分析与结构优化[J].纸和造纸, 2013, 32(11): 17.

[6] Chen Ke-fu. Pulp and paper machinery and equipment(below)[M]. 3ed. Beijing: China Light Industry Press, 2011.

陈克复. 制浆造纸机械与设备(下)[M]. 3版. 北京: 中国轻工业出版社, 2011.

[7] Shi Hei-jiu San-lang, with the latest theory and practice of papermaking technology[M]. Zhang Ercong, translated. Beijing: China Light Industry Press, 1989.

石黑久三郎, 著. 最新造纸技术的理论与实践[M].张尔聪, 译. 北京: 中国轻工业出版社, 1989.

[8] Liu Wei. Based on the CFD modern papermaking machine cloth technology and cloth pulp research[D]. Guangzhou: South China University of Technology, 2013.

刘 伟. 基于CFD的现代造纸机布浆技术与布浆器的研究[D]. 广州: 华南理工大学, 2013.

[9] Yang Xu, Chen Ke-fu, Wen Hai-ping. Principle and New Calculating Methods of High Pressure and Wide Headbox Equivalent Pressure Blender[J].China Pulp & Paper， 2009, 28(9): 1.

杨 旭, 陈克复, 文海平. 高速宽幅流浆箱等压布浆器原理及新的计算方法探讨[J].中国造纸, 2009, 28(9): 1.

[10] Liu Jian-an, Chen Ke-fu, Fan Hui-ming, et al. Limitation analysis of cone pipe cloth[J].Transactions of China Pulp and Paper, 2005, 20(1): 161.

刘建安, 陈克复, 樊慧明, 等. 锥管布浆的局限性分析[J].中国造纸学报, 2005, 20(1): 161.