基于变精度相容粗糙集的作战装备消耗预测研究

陈博，徐常凯，任佳成

（空军勤务学院 航材管理系，江苏 徐州221000）

作战装备保障是指在实际任务的环境中，装备保 障部队对作战部队供应所需维护与维修作战装备，从而确保作战部队顺利完成作战任务的后勤保障活动。它是装备保障工作的重要组成部分，为了确保战时装备保障的顺利进行，装备保障部队执行作战任务之前往往要对装备消耗情况进行预测，从而保证装备保障的顺利实施，这不仅有利于实现军事目标，还能获得极大的经济效益[1]。文中通过对影响战时装备保障的因素进行统计分析，并建立变精度相容粗糙集模型对这些影响因素进行约简，最终实现对战时装备的消耗预测。其中变精度相容粗糙集模型可以实现对属性的约简，大大简化相关规则，去除对战时装备消耗影响较小的因素，并且其对噪声具有很强的抗干扰能力，从而使预测更加合理精确[2]。

1 作战装备消耗的影响因素分析

战时装备保障具有装备消耗量巨大、影响因素多、保障条件恶劣等特点，作战装备保障部队担负的作战任务和战略地位极其重要。为提高装备完好率、部队战斗力，确保战时装备在执行作战任务的过程中发挥最大的战斗力，需要重点分析战时装备保障消耗预测的相关影响因素，提高战时装备保障成效。文中使用变精度相容粗糙集模型，针对某作战飞机在执行不同作战任务时的某项装备的消耗情况，对相关影响因素进行属性约简。主要的影响因素有以下几点[3]：

1）任务战损率。任务战损率主要指飞机在执行不同作战任务的过程中，发生损伤概率的大小。

2）历史消耗数据。历史消耗数据对预测消耗情况有很好的借鉴意义，相同的飞机在相似的任务环境下执行相同任务，其战时装备数量的消耗的变化范围相对较小。

3）地理环境。不同的战区环境、战场地势对战时装备消耗量的影响是显而易见的。例如西部战区主要是内陆地区，气候相对干燥，而东部战区沿海地区较多，气候相对湿润，所以在东部更易发生腐烂与变质，消耗量大。

4）任务时间。针对不同任务的任务强度、飞机出动的架次可计算出其任务时间，任务时间的长短也对装备的消耗有一定影响。

文中主要研究上述四种要素对战时装备消耗量的影响，利用已有的数据对各影响因素的重要性进行比较，去除影响相对较小的因素[4]。

综上所述，对于作战装备消耗因素的影响很多，但部分因素难以进行量化和数据统计，各因素之间也有相互重叠的影响。针对某一机型在执行某项特定作战任务的情况下经过分析，筛选出对装备消耗影响较大的六种因素即所属战区、地形、历史消耗情况、战损率、任务时间，下一步利用已有的数据对各影响因素的重要性进行比较，去除影响相对较小的因素。

2 作战装备影响因素的约简

Pawlak经典粗糙集理论模型是在不可分辨关系的基础上的一种数据挖掘方法，首先在论域范围内建立二元等价关系，再通过等价关系对等价类进行划分，构造出论域的上、下逼近算子，最后用这对逼近算子不断地逼近目标[5]。

定义1：设U≠∅，U是该研究范围的论域。对于任意的X包含于U，则称X为U中得到一个概念或范畴。U中的一个概念族F={X1,X2,…,Xn}称为关于U的知识，其中Xi包含于

定义2：设R是U上的一个等价关系，U/R={X1,X2,…, Xn}表示R产生的分类，称为关于U的一个知识。表示关系R下包含元素x的等价类。（U,R）称为近似空间。

定义3：若P包含于R，且P不为空集，则P中全部等价关系的交集称为P上的不可分辨关系，记为IND（P）:

不可分辨关系也称为等价关系，它把 U划分为有限个集合，称为等价类。在每一个等价集合中，对象间是不可分辨的。对于∀x∈U 它是P等价类，定义为[6]：

定义4：令X属于U，R是U上的一个等价关系。则对于X的粗糙集可以上近似和下近似来描述[7]：

由于经典粗糙集理论对不可分辨关系过于苛刻，对预测数值的精度要求非常高，往往一点偏差，就会使粗糙集的上、下近似集发生改变，从而导致模型无法将它们归为一类，造成了大量的误差。为了提高粗糙集模型对噪声的抗干扰能力，研究人员不断地对粗糙集模型进行扩展，建立了变精度模型、优势粗糙集、相容粗糙集等。文中将变精度粗糙集与相容粗糙集相结合，处理多值决策系统，并提高预测精度对战时装备的携带属性进行准确预测。

变精度相容粗糙集有两种模型，模型1是其目标概念的下近似和边界域的交集相交；模型2是其目标概念的下近似和边界域的交集为空。文中研究的战时装备保障由于任务重的偶然性较大，噪声引起的数据不一致性问题也相对较大。由于模型1是将逼近算子引入到模型中，其允许一定程度的错误分类率存在，因此文中选用模型1进行预测。

变精度粗糙集的上、下近似集为[8]：

设SP(X)为属性P下与x可能相容的最大对象的集合，则：

SP(X)相容关系的粗糙上、下近似集为：

将这两者相结合[9]，设（U,T）是相容逼近空间，其中U为非空有限论域，T为U上的相容关系，对于子集 X属于 U，0≤β≤0.5，则上、下近似集以及边界域与正、负域可表示为：

且在变精度相容粗糙集模型1中满足：

3 变精度相容粗糙集模型的运用

首先将装备的消耗状况划分为三类，即“无消耗”、“低消耗”与“高消耗”。将飞行员飞行水平分为高水平与低水平两种，将任务时间分为长时间与短时间两种，将地理环境分为五大地区，并在此基础上分为高原、沿海、沙漠、平原四种地形。对某项飞机装备收集各不同任务时的消耗数据进行统计，再列出差别矩阵，通过差别矩阵对属性进行约简，最终通过变精度的粗糙集模型对规则进行陈述总结[10]。

针对某项装备在装备保障部队执行具体不同条件下战时装备保障任务时的携带属性作了判断，具体的影响因素与结论见表1。包括历史消耗情况、任务战损率、飞行任务时间、地理环境以及所属战区，通过运用变精度相容粗糙集模型对携带属性即该装备在执行任务中必带、可带还是不带的规则进行预测。

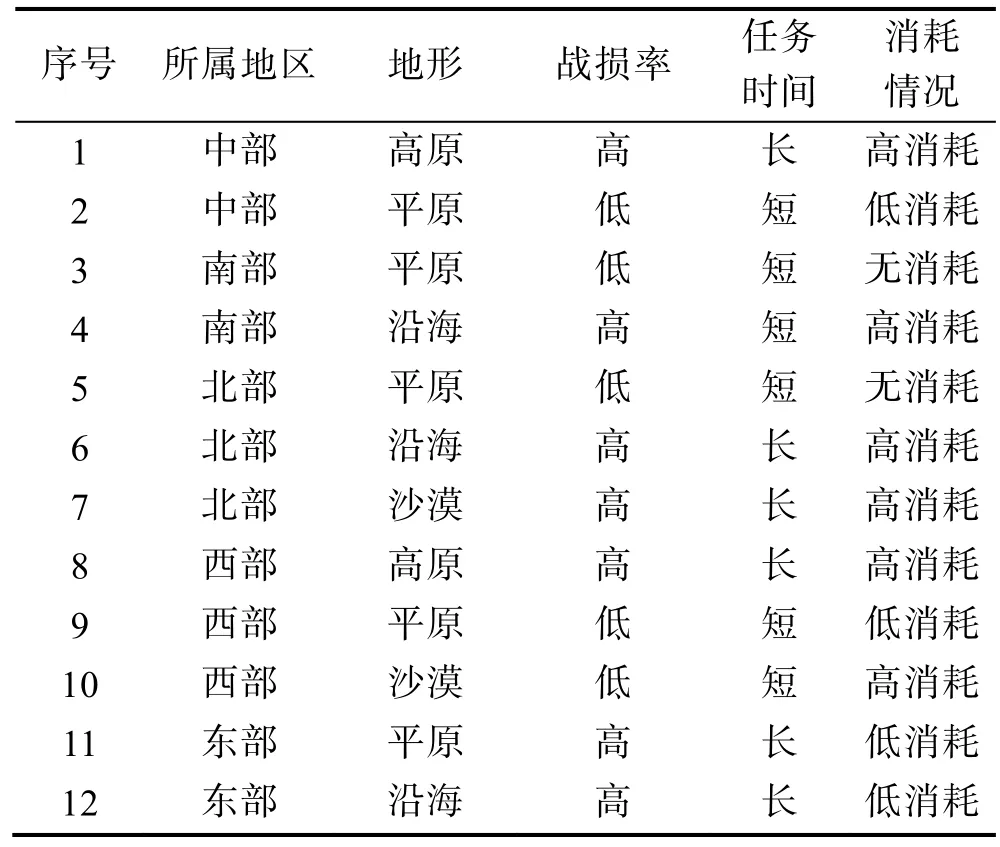
表1 影响携行属性的因素及决策

其中所属地区与地形有一定的相互影响关系，固定地区有其相对应的地形地貌。例如东部地区基本上是平原、沿海地形，所以将地区和地形进行相容处理，合并为地理信息列。为了方便表示，在地理环境中的数字和字母的含义分别为：1——中部地区、2——南部地区、3——北部地区、4——西部地区、5——东部地区；a——高原地区、b——平原地区、c——沿海地区、d——沙漠地区。根据有关资料与经验，将战损率小于0.5的定义为低战损率、高于0.5的定义为高战损率。任务时间小于等于1天的认为任务时间属于短时间，大于1天的任务作为长任务时间。在历史消耗情况中，装备以往消耗数小于3的定义为低消耗、大于等于3的定义为高消耗，并将各个不同的属性条件进行量化，得到信息表2：

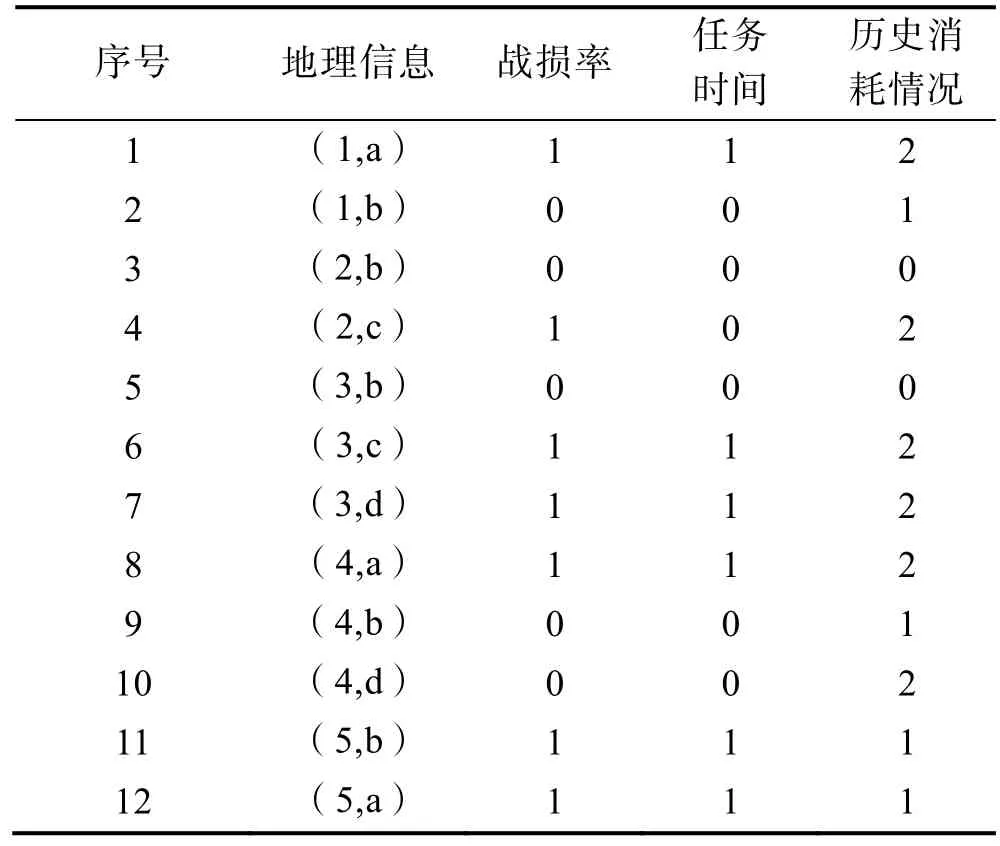
表2 决策量化信息表

设属性约简前的属性集合为P，约简后的属性约简集合为 Q，对于表 2集合 U/IND（P）={{1,4,6,7,8,10}，{2,9}，{3,5}}根据集合的分类。首先进行属性的约简，去除在战时装备保障过程中对该项装备影响不大的冗余的因素。A表示地理环境，B表示战损率，C表示任务时间。

对于集合 U，若有等价关系 r={r1,r2,r3}，其中r∈ R,若 IND(R)=IND(R－r)，则对应的 A，B，C，D中的一种属性是没有必要的。通过属相约简即可得到核属性Core，使P，Q两个属性集合，其中 Q包含于 P，符合下面两个条件[11]：IND(P)=IND(Q)；

由此可以列出差别矩阵，见表3。

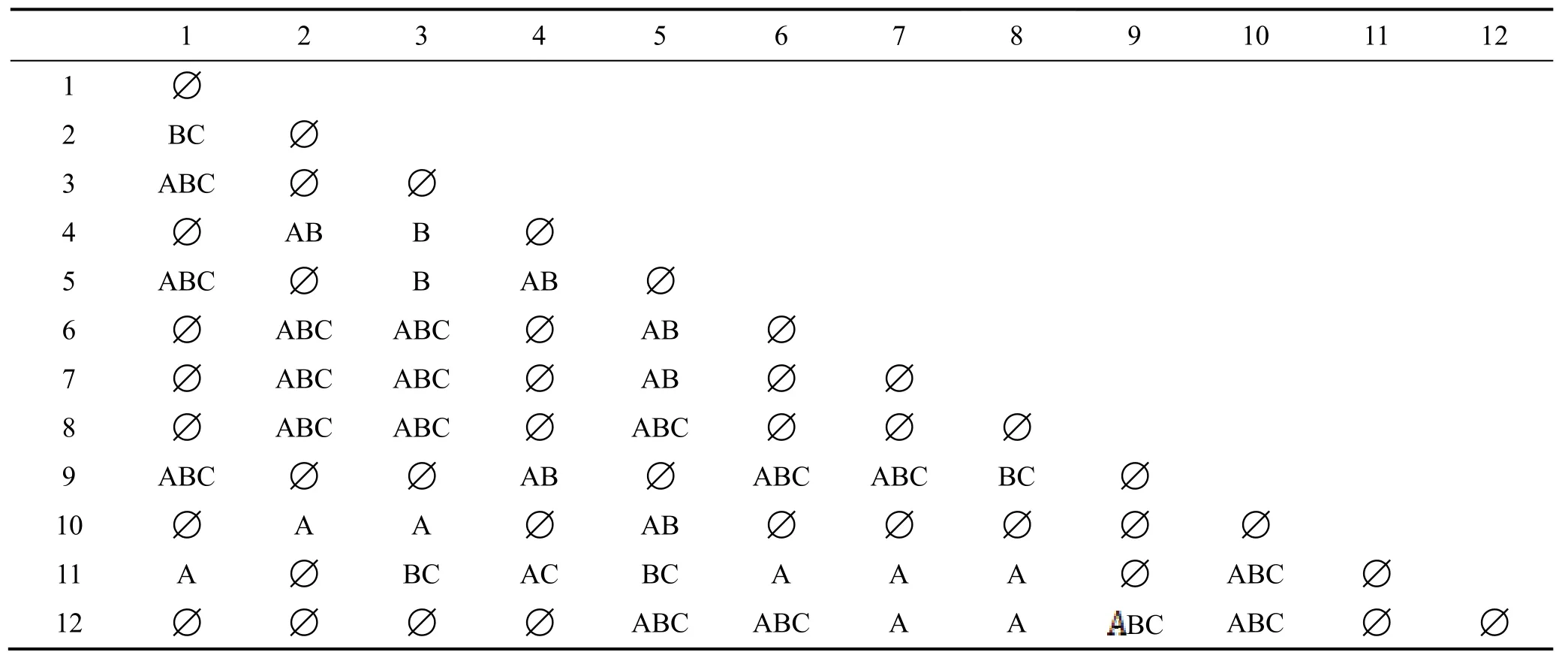
表3 差别矩阵

经 过 简 化 指 标 为 fs= (A ∨ B ∨ C)∧ (B∨C)∧(A ∨ B)∧ A ∧ B=A ∧ B，由fs可知决策类S的决策核属性 Core(P)为{A，B}，约简属性为 RED(P)={C，D}，Core(P)=∩ RED(P)。

由表 3可知，系统有三个决策类，用 X1表示高消耗，X2表示低消耗，X3表示无消耗：X1={1 ,4,6,7,8,10}, X2={2 ,9,11,12}, X3= {3 ,5}。

以集合X1与X2之间的关系为例，由变精度相容粗糙集模型1性质可知：

由此计算出相容类为：

通常变精度β为0≤β≤0.5，通过综合分析与以往的经验取精度β为 0.3，再由变精度的上下近似集得到三个决策类的近似域分别为：

得出确定性规则：（A={*,a}）和（B={高}）»“该项装备高消耗类装备”；（A={*，c}）和（B={高}）»“该项装备低消耗类装备”

可能性规则：（A={*，b}）和（B={无}）»“该项装备低消耗”或“该装备不消耗”；（A={*，b}）和（B={低}）»“该项装备低消耗”或“该装备不消耗”；（A={*，b}）和（B={高}）»“该项装备低消耗”或“该装备高消耗”。

从以上规则与结论出发，对于该项装备得到以下结论：当在高原、沙漠地区执行战时装备保障任务时，该项作战装备消耗量大；在沿海地区执行战时装备保障任务时，该项作战装备消耗量小；在平原地区执行战时装备保障任务时，该项装备消耗量小甚至无消耗；在平原地区执行战时装备保障任务时，该项装备为高消耗。

通过以上决策规则，可以对不同种类的装备在不同任务环境中的消耗情况进行预测，从而做到战时装备的精确保障，节约了携带成本，避免产生大量的运输成本。

4 结语

文中主要通过发挥粗糙集可以对数据进行挖掘并定性分类的优势，将变精度与相容粗糙集进行融合，从变精度与相容粗糙集的上、下近似集入手建立模型，并具体以某一项装备消耗数据为例，对影响该某项装备在作战装备保障过程中的多种消耗因素进行了分析。约简掉不重要的因素，再利用变精度相容粗糙集模型对数据进行处理，最终得到该项装备的消耗预测规则。通过此方法有利于加强对战时装备预测的精准度，大大地节省了装备的物流成本，使战时装备保障不仅仅能保证满足完成任务的需要，同时也可以提高经济效益。

参考文献：

[1] 何亚群, 柏林, 赵福军, 等. 航材供应学[M]. 徐州: 空军勤务学院出版社, 2012.

[2] 柏林, 史霄霈. 航材法规知识[M]. 徐州: 空军勤务学院出版社, 2012.

[3] 项华春, 陈云翔. 基于仿真的飞机战损部位及备件需求确定[J]. 火力与指挥控制, 2009, 34(8): 41-43.

[4] 辛后居, 崔崇立. 航材管理信息系统[M]. 徐州: 空军勤务学院出版社, 2012.

[5] 王鹏等. 美军战时装备保障的特点及启示[J]. 海军装备, 2008(9): 6-7.

[6] 何亚群, 胡寿松. 军机备件需求量修正的粗糙集方法[J]. 中国管理科学, 2003(5): 42-45.

[7] 张文修, 梁吉也. 粗糙集理论与方法[M]. 北京: 科学出版社, 2001.

[8] 翟俊海, 翟梦尧, 高原原, 等. 变精度相容粗糙集模型[J]. 计算机工程与应用, 2012, 48 (26): 134-138.

[9] 何亚群, 胡寿松. 不完全信息的多属性粗糙决策分析方法[J]. 系统工程学报, 2004, 19 (2): 117-120.

[10] 张云淘, 龚玲. 数据挖掘原理与技术[M]. 北京: 电子工业出版社, 2004.

[11] 苗夺谦, 李道国. 粗糙集理论算法与应用[M]. 北京:清华大学出版社, 2008.