一种改进粒子群算法的立体阵列优化方法

樊征兵，李 阳，宋亚辉，张武林

(中国飞行试验研究院，陕西西安710089)

0 引 言

近些年来，许多专家致力于传声器阵列优化设计的研究，传声器阵列也从一维线阵列发展到二维平面阵列和三维立体阵列。对于线阵列，由于阵元的线形分布导致其无法对声场进行二维或更高维的重建。二维平面阵列也存在明显的缺点。如果声源距离平面阵列较近，那么平面阵列对声源在阵列前或后的位置就无法做出准确判断，而且使用平面阵列对汽车或飞机内部密闭空间的声源进行识别时，存在较大的困难。三维立体阵列弥补了一维线阵列和二维平面阵列的上述缺陷。在三维立体阵列中，星形立体阵列设计简单，变量参数容易控制，阵列具有较好的指向特性，而且对后向噪声具有一定的抑制作用。因此，本文选择星形立体阵列进行优化。

目前，在阵列优化设计中，主要的智能算法包括遗传算法[1-3]、模拟退火算法[4-6]、蚁群算法[7-8]和粒子群算法[9-12]等。遗传算法作为一种全局优化算法，因其鲁棒性强、实用高效等特点被广泛应用于阵列优化设计中，但是与后面三种智能算法相比，其需要对问题进行编码和解码，编程实现比较复杂。另外，遗传算法中的交叉概率和变异概率严重影响了算法求解的品质，而这两个参数的选择在很大程度上依靠经验。此外，遗传算法搜索速度慢，目前很多遗传算法的改进都是结合其他算法进行的[10]。模拟退火算法虽然同样能够得到问题的全局最优解，但是由于模拟退火算法对整个搜索区域不甚了解，使得其运算效率不高，而且模拟退火算法对初始温度的依赖性很强，进化速度较慢。蚁群算法具有较强的鲁棒性，需要设置的参数少，但是如果参数设置不当，就会导致求解速度非常慢，而且所得解的质量特别差，通常情况下，蚁群算法计算量大，求解所需时间较长。粒子群算法以其容易实现、精度高、收敛快等优点被广泛应用于全局优化的问题中，尤其在求解连续问题时，粒子群算法显示了非常明显的优越性。但是，粒子群算法也有其自身固有的缺点，如由于收敛快，容易导致出现早熟现象，尤其对复杂问题的优化，不结合其他方法或者对算法进行改进，很难获得全局最优解。本文在传统粒子群算法的基础上，通过对算法的迭代进行先“粗”优化后“细”优化的策略，达到改进算法的目的。

1 星形立体阵列模型和声学性能

图1为平面波入射到星形立体阵列的模型，其中ℓ= 1 ,2,… ,L为星形立体阵列臂数，信号入射方向为(θ,ϕ)，其中θ为信号入射方向与z轴夹角，即信号俯仰角，ϕ为信号入射方向在xoy平面的投影与x轴正向夹角，称为方位角。星形立体阵列第ℓ臂的安装角为(θℓ,ϕℓ)。利用波束成形方法推导得到的阵列的指向特性为

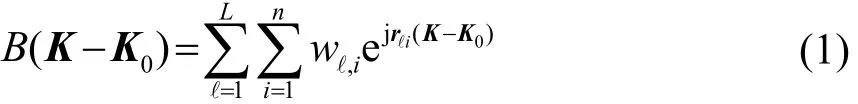
其中，wℓ,i为第ℓ臂上第i个阵元的加权系数，为突出阵列本身的指向性，本文加权系数全部取1；rℓ,i为第ℓ臂上第i个阵元到参考点(本文选择坐标原点(0,0,0)为参考点)的距离向量；K=-k⋅κ为(θ,ϕ)方向的入射波矢量，k= 2 π/λ为波数，λ为入射波的波长，κ= (sinθcosϕ,sinθsinϕ,cosθ)为入射波单位矢量；K0=-k⋅κ为目标信号的入射波矢量，本文假设目标信号入射方向为(0,0)，则κ0= ( 0,0,1)；n为每个臂上的阵元数

阵列旁瓣水平(Sidelobes Levels，SL)经归一化处理后定义为：

式中为归一化旁瓣水平，Ω为旁瓣区域。

阵列的优化目标函数为

式中为主瓣宽度。阵元位置约束条件为

将第n个阵元固定在直杆最外端，可以有效地降低阵列的主瓣宽度；将第1个阵元固定在直杆rmin处，可以有效抑制主瓣附近的旁瓣水平，r0为相邻阵元的最小间距。

图1 星形立体阵列模型Fig.1 Star-shaped 3D array model

2 改进的粒子群算法

2.1 传统粒子群算法

星形立体阵列的优化为搜索优化目标的全局最优解，阵列的优化目标则为最小化主瓣宽度和旁瓣水平，见公式(3)。在粒子群算法中，每个粒子表示一种布阵方式，所有粒子根据适应度函数不断更新个体极值和种群极值，最终得到全局最优解。如果一个粒子群包含N个D维的粒子，则第k代粒子群的位置Xk可表示为

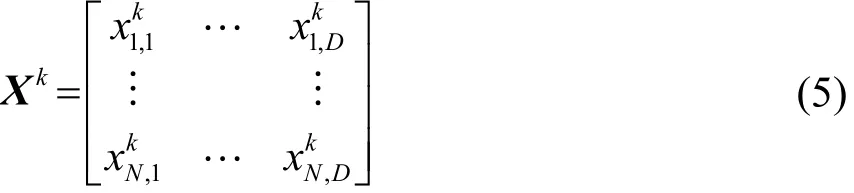
第k代粒子群速度Vk可表示为

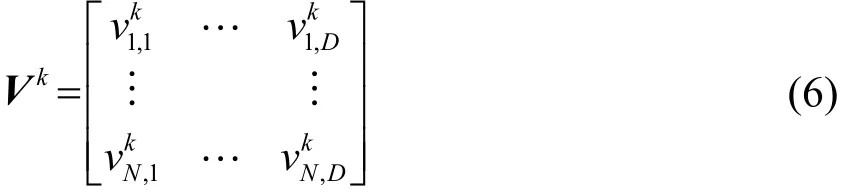
第k代粒子个体的历史最优值Pk可表示为

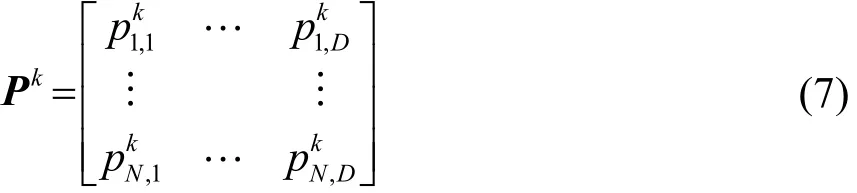
第k代粒子群历史最优值Gk可表示为

粒子位置和速度根据式(9)更新：

式中：ω为线性递减惯性权重，ω表达式见式(11)；c1和c2分别为粒子认知系数和社会系数；µ1和µ2为0～1之间均匀分布的随机数。

式中：ωmax和ωmin分别为最大和最小惯性权重；kmax为最大进化代数。

2.2 改进粒子群算法(IPSO)

在使用传统的粒子群算法对本文5臂30阵元的星形立体阵列进行优化时，如果对 30个阵元中的 20个阵元同时进行优化，算法计算时间较长，而且结果往往只优化到局部解。为了解决这个问题，本文提出了一种改进粒子群算法。改进粒子群算法的一般步骤为：

(1) 降维处理：将粒子维数由原来的L(n- 2 )降为n-2。具体操作为：任意选择1臂作为优化臂，对优化臂上除固定阵元外的其他阵元进行优化，剩余L-1个臂上的阵元坐标由优化臂上的阵元旋转获得；

(2) 初始化前半部种群：同时初始化S(S＞L)个种群，每个种群规模为N，粒子维数为n- 2，设置最大进化代数k1max为停止条件；

(3) 并行优化上述S个种群，利用式(11)更新粒子惯性权重，利用式(9)、式(10)更新粒子速度、位置；

(4) 满足停止条件后，根据式(3)的目标函数选择L个最优粒子群组成L+1个阵列，具体方法为：

a) 前L个阵列：在S个粒子群中选择最优的前L个粒子群，每个粒子群构成阵列的参考臂，共L个参考臂。把每个参考臂绕图1所示的z轴旋转l*360°/L(l=1,2,…，L-1)，1个参考臂经过L-1次旋转后，便生成了1个包括参考臂在内共L个臂的阵列，因为有L个参考臂，所以共有L个这样的阵列。

b) 第L+1个阵列，a)中的L个最优粒子群，对应图1中的L个臂，将这L个臂按照一定规律排列，使相邻的两个臂在xoy平面的投影相隔360°/L。

(5) 初始化后半部种群：将步骤(4)得到的L+1个阵列表示为新的粒子群，新粒子群的种群规模为L+1，粒子维数为

(6) 对新粒子群继续进行优化，此时取最小惯性权重，满足停止条件后输出最优结果。

改进粒子群算法主要分两部分：前半部为步骤(1)、(2)和(3)，目的是对粒子降维，得到中间解。后半部为步骤(4)、(5)和(6)，目的是降低种群规模，对中间解进行更精细的优化。

算法流程如图2所示。

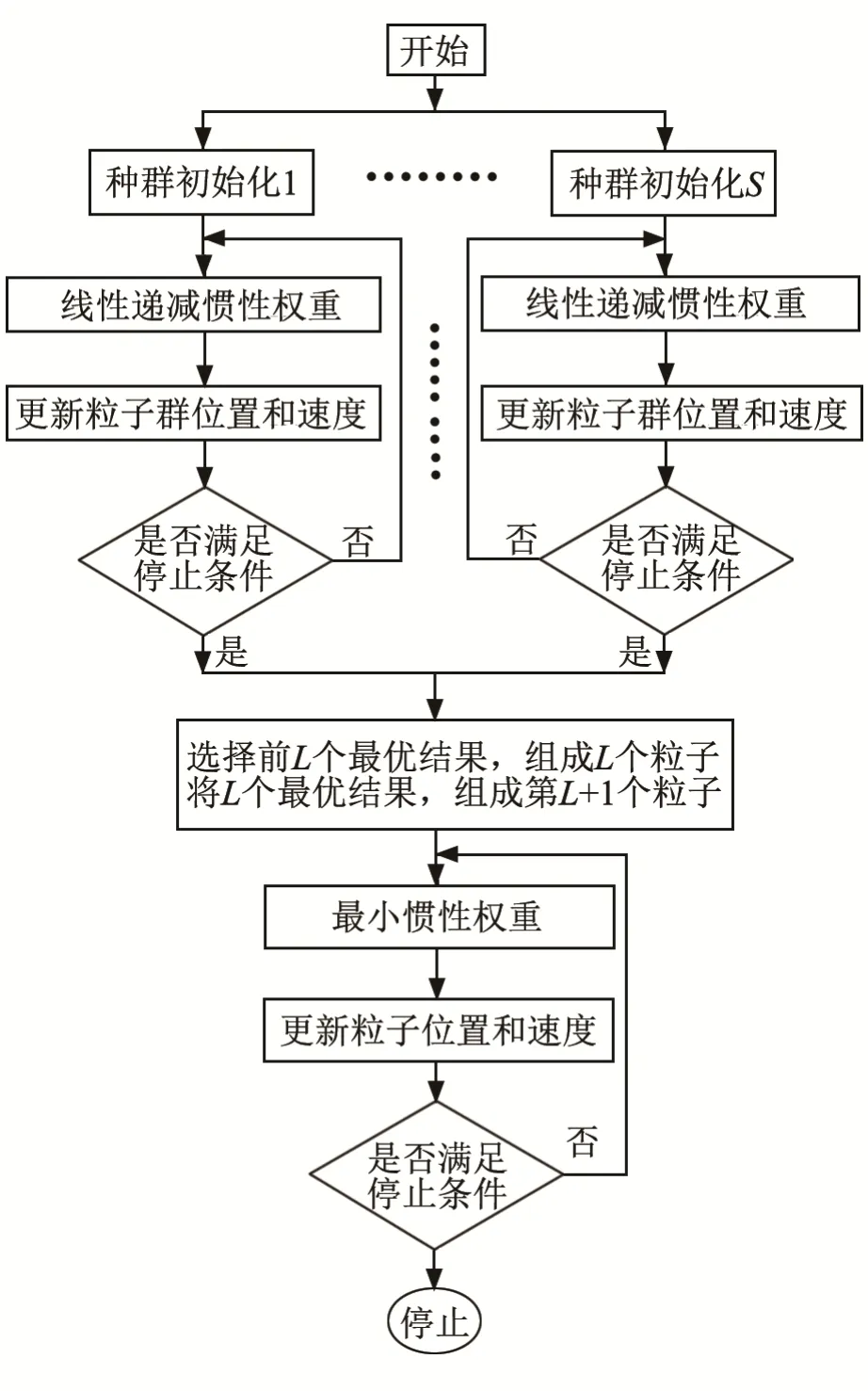
图2 IPSO算法流程图Fig.2 The flowchart of the IPSO algorithm

3 仿真实验

假设一个5臂星形立体传声器阵列，L=5，阵列每臂的直杆上分布6个传声器，n= 6，每根直杆在rmin和rmax处各固定1个传声器，共固定10个传声器。每根直杆与z轴的夹角为 60°，5根直杆在xoy平面内的投影在 360°内等分。rmin= 0 .2 m，rmax=2 m。

选择1000 Hz作为信号的分析频率，在仿真实验之前，对式(3)的目标函数做如下简化：

式中：k1为主瓣宽度加权系数；k2为旁瓣水平加权系数，且k1+k2=1。

将式(12)作为本文改进粒子群算法的适应度函数。经过多次实验验证，当主要优化主瓣宽度时，取当主要优化旁瓣水平时，取

线性递减惯性权重粒子群算法(Linearly Decreasing Inertial Weight Swarm Optimization Algorithm, LDWPSO)和本文改进粒子群算法(IPSO)进行比较，两种算法的参数设置为：

(1) LDWPSO：种群规模为30，最大迭代步数为 1000，线性递减惯性权重为

(2) IPSO前半部：线性递减惯性权重：

(3) IPSO后半部：最小惯性权重：

(4) 两种算法适应度函数选择式(12)，主要优化旁瓣水平。

(5) 入射波俯仰角θ范围为 0～30°，其中，0～10°之间步长取 0.2°，10.5～30°之间步长取 1°。方位角ϕ的范围为0～180°，步长取10°。

(6) 本文对适应度中的主瓣宽度进行归一化处理：旁瓣水平用式(2)作归一化处理。

3.1 IPSO算法与LDWPSO算法的优化比较

本文改进粒子群算法(IPSO)和 LDWPSO算法各执行5次，取各自的最优者进行比较，结果如图3所示。

图3 两种算法的比较Fig.3 The comparative diagram of the two algorithms: LDWPSO and IPSO

通过图3可以看出，LDWPSO算法虽然设置迭代1000步为停止条件，但是，当算法迭代到800步时已经收敛到局部解。本文IPSO算法在前半部分(图3实线起始位置)的降维优化中，已经得到比LDWPSO算法更优的结果，在后半部(图3实线)进行更精细的优化，进一步得到了更优的结果。

LDWPSO算法和 IPSO算法的优化时间见表1(仿真实验电脑配置为 Intel(R) Core(TM) i5 CPU M460@2.53 GHz 1.19 Ghz, 2.98 GB内存)。

表1 5次优化平均时间Table 1 The average time of 5 times optimization

在表1中，与LDWPSO算法相比，本文IPSO算法的计算时间明显下降。所以采用先降维再降种群规模的方法，可以达到对算法时间和结果进行优化的目的。

3.2 阵列的主瓣宽度和旁瓣水平分析

图4为本文改进粒子群算法优化后的阵列二维俯视图，对应的阵元坐标如表2所示。图5为LDWPSO算法优化后的阵列二维俯视图，对应的阵元坐标如表3所示。

仿真1：频率在1000 Hz时，分别计算图4和图5阵列的指向性图，仿真结果见图6～7。

图4 采用IPSO算法优化阵列的俯视图Fig.4 The top view of the optimized array by IPSO algorithm

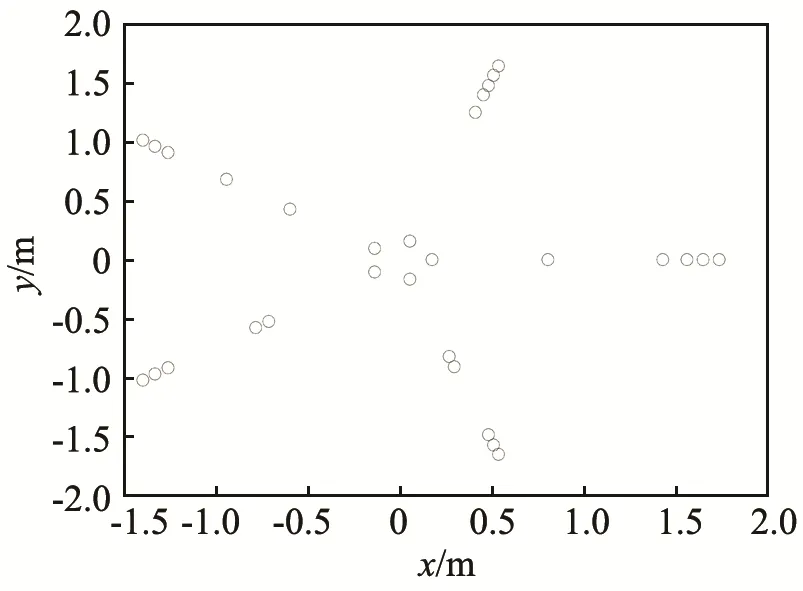
图5 采用LDWPSO算法优化阵列的俯视图Fig.5 The top view of the optimized array by LDWPSO algorithm

表2 阵元坐标(IPSO)Table 2 The Cartesian coordinates of the array elements for IPSO algorithm

观察图5可以发现，LDWPSO算法得到的阵列阵元集中在外端。如果阵元集中在外端，会相应增大阵列的有效孔径，对降低阵列的主瓣宽度有利，而降低阵列主瓣宽度势必会造成阵列旁瓣水平的恶化。比较图6和图7可以看出，LDWPSO算法得到的阵列与IPSO算法得到的阵列相比，最大旁瓣级出现了明显的恶化，在具体量值上，虽然LDWPSO算法的主瓣宽度降低了6.9%，但是旁瓣水平提高了41.2%。

在500～3000 Hz的频率范围内，利用图4和图5的阵列分别计算主瓣宽度和旁瓣水平，计算结果如表4和表5所示。

从表4和表5可以看出，在优化旁瓣水平的前提，与LDWPSO算法相比，IPSO算法达到了优化的目的，但同时也看到，当单独优化旁瓣水平时，不可避免地造成了主瓣宽度的恶化，特别是在低频情况下，这是因为主瓣宽度与频率和阵列孔径之间成反比。

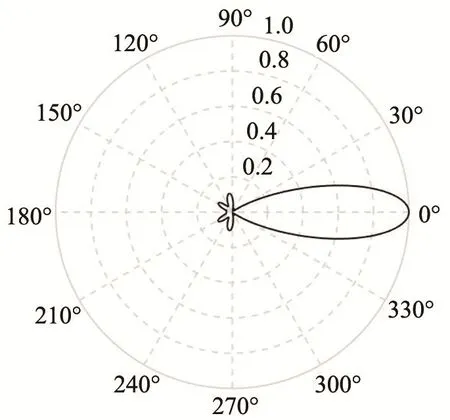
图6 IPSO算法优化阵列的指向图Fig.6 The directivity pattern of the array with the IPSO algorithm

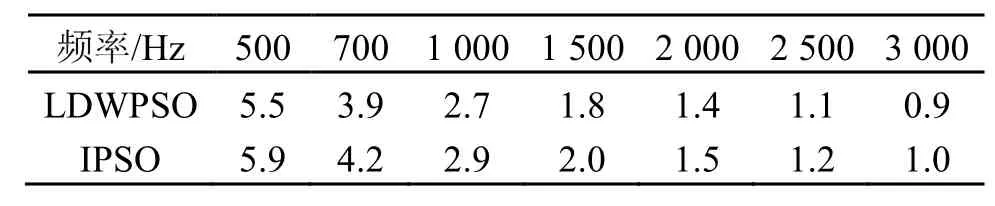
表4 两种阵列的主瓣宽度比较(°)Table 4 Comparison between the main lobe widths ofthe two arrays (°)

图7 LDWPSO算法优化阵列的指向图Fig.7 The directivity pattern of the array with the LDWPSO algorith m

表5 两种阵列的旁瓣水平比较(dB)Table 5 Comparison between the side lobe levels of the two arrays (dB)

3.3 信号源个数对阵列指向性的影响

通过2个仿真实验，分析了信号源个数对阵列指向性的影响。

仿真2：信号频率为1000 Hz，信号源入射方向为(15°，0°)，图8和图9分别给出了图4和图5阵列在两种算法下的阵列指向性等值线的仿真结果，图中“+”为信号源，图中右侧色棒代表归一化后的声压值(以下同)。

仿真3：信号频率均为1000Hz，两个信号源入射方向分别为(20°，130°)和(10°，-120°)，仿真结果见图10～11。

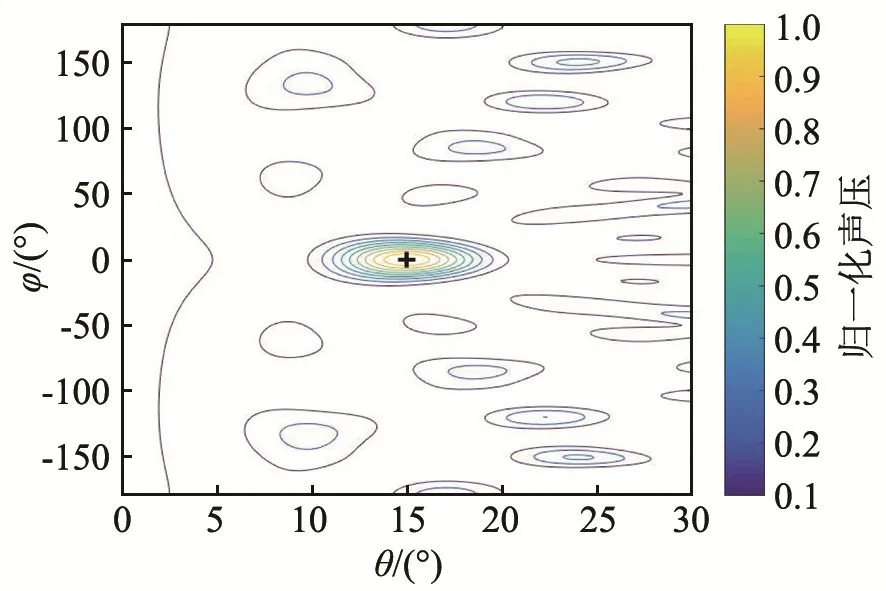
图8 入射方向为(15°，0°)时，IPSO算法阵列指向性等值线仿真结果(f =1000 Hz)Fig.8 The array output with the IPSO algorithm in the direction of incidence is (15°, 0°), plotted in terms of constant contours over a scanning plane (f =1000 Hz)

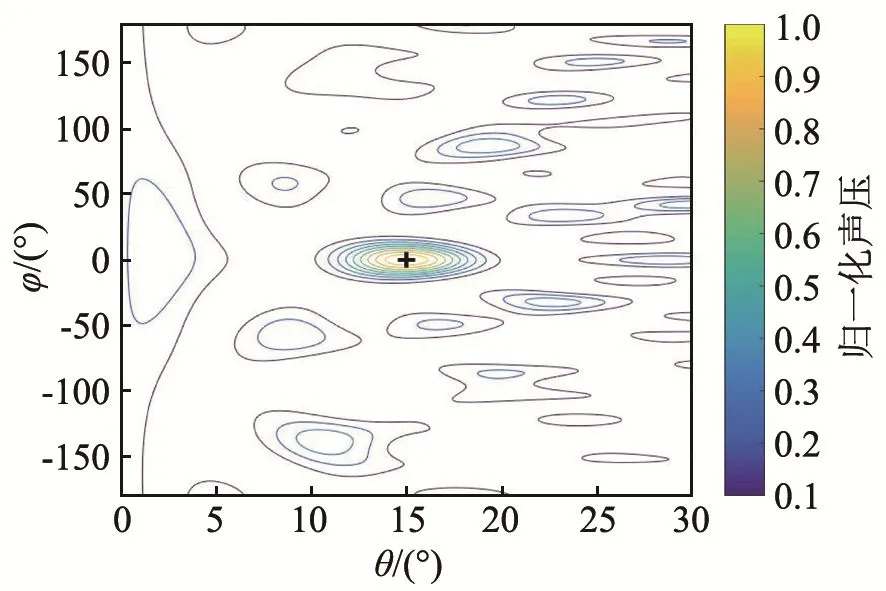
图9 入射方向为(15°，0°)时，LDWPSO算法阵列指向性等值线仿真结果(f =1000 Hz)Fig.9 The array output with the LDWPSO algorithm, in the direction of incidence is (15°, 0°), plotted in terms of constant contours over a scanning plane (f =1000 Hz)

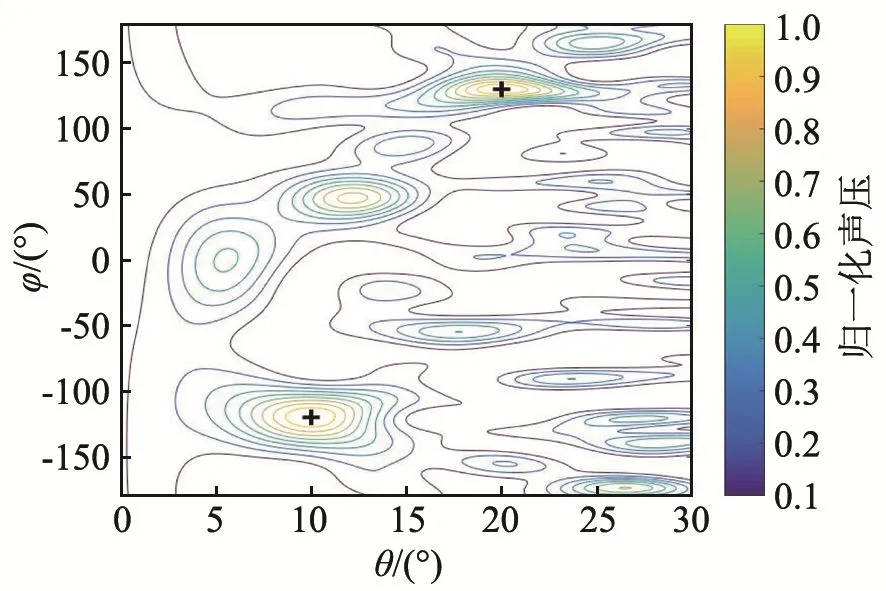
图10 双信号源时IPSO算法阵列指向性等值线仿真结果(f =1000 Hz)Fig.10 The array output with the IPSO algorithm for two signal sources, plotted in terms of constant contours over a scanning plane (f =1000 Hz)

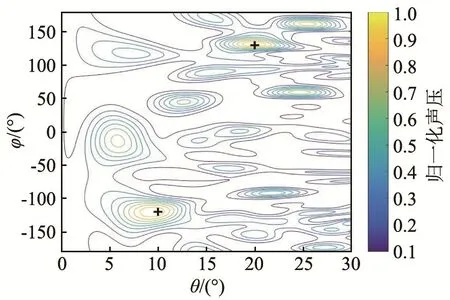
图11 LDWPSO算法阵列指向性等值线仿真结果(f =1000 Hz)Fig.11 The array output with the LDWPSO algorithm, for two signal sources, plotted in terms of constant contours over a scanning plane (f =1000 Hz)

利用两种算法得到的阵列同时对 1～2个信号源进行方位识别。由图8～11可以看出，2种阵列均可有效识别信号源方位，但是IPSO算法得到的阵列对旁瓣的抑制效果更好。随着信号源个数的增加，波束成形计算结果的干扰增加，这是算法自身的缺点，若要去除干扰，需要对波束成形方法进行改进。

3.4 信噪比对阵列指向性的影响

同理，通过仿真实验，对信噪比对阵列指向性的影响进行分析。

仿真4：信号频率为1000 Hz，信号源入射方向为(15°，0°)，信噪比从-10～20 dB 变化时，观察图4和图5阵列的角度估计误差随信噪比的变化情况，仿真结果见图12。

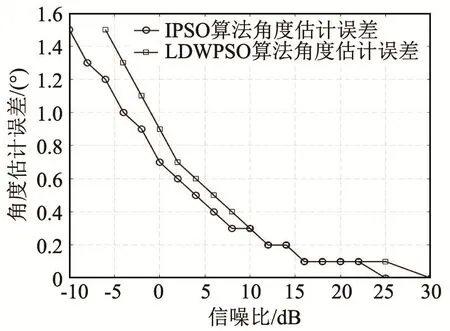
图12 2个阵列的角度估计误差Fig.12 Error of angle estimation for the two arrays

角度估计误差表达式为

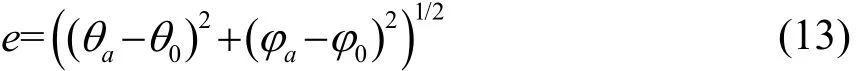
式(13)中，表示估计角度，表示真实角度。

从图12可以看出，与LDWPSO算法的角度估计误差相比，IPSO算法的角度估计误差更低，特别是在低信噪比情况下，LDWPSO算法在低于-8 dB信噪比时，已经无法确定信号源位置(图12中未画出)。当信噪比大于25 dB时，背景噪声对IPSO算法已经没有影响，而同样的情况在 LDWPSO算法中信噪比必须达到30 dB。

3.5 空间角对IPSO算法阵列指向性的影响

空间角对IPSO算法阵列指向性的影响，仍然通过仿真实验进行分析。

仿真5：设空间有一信号源，保持方位角不变，俯仰角θ从10°～80°变化，信号信噪比从5～30 dB变化，观察俯仰角变化引起的角度估计误差的变化，仿真结果见图13。

仿真6：保持俯仰角不变，方位角ϕ从-180°～135°变化，信噪比(SNR)从 5～30 dB 变化，观察方位角变化引起的角度估计误差的变化，仿真结果见图14。

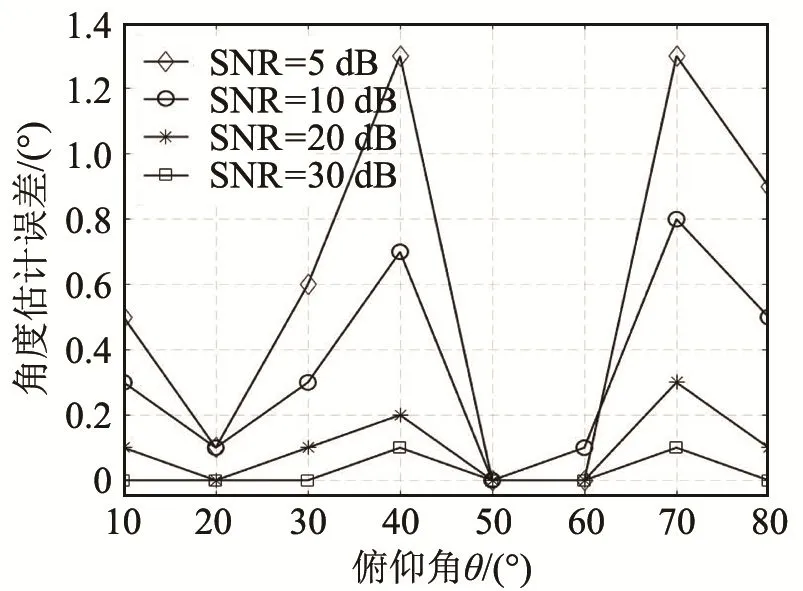
图13 IPSO算法阵列角度估计误差(φ =0°)Fig.13 Error of angle estimation using the array obtained by the IPSO algorithm (φ =0°)

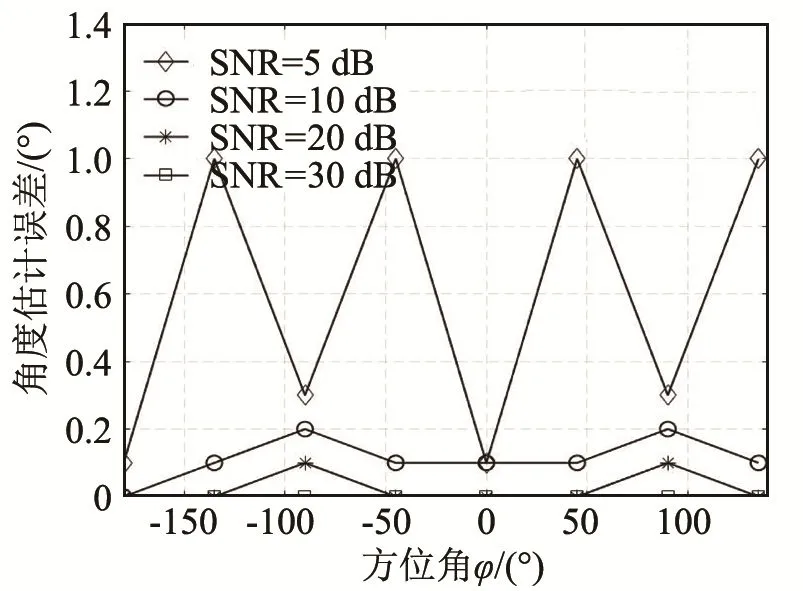
图14 ISPO算法阵列角度估计误差(θ=20°)Fig.14 Error of angle estimation using the array obtained by the IPSO algorithm(θ=20°)

分析图13可知，入射信号方位角保持不变，当信噪比大于等于20 dB时，俯仰角的变化对阵列的角度估计误差影响比较小，阵列指向性表现平稳，当信噪比小于等于10 dB时，阵列的角度估计误差随俯仰角的变化较为明显，尤其俯仰角在 40°和70°附近，阵列的角度估计误差对俯仰角的变化非常敏感。对于从40°和70°入射的信号，可以将阵列与信号的相对俯仰角调整到50°～60°之间，以此来降低信噪比对俯仰角在 40°和 70°附近的入射信号的影响。

分析图14可知，入射信号俯仰角保持不变，当信噪比大于等于10 dB时，信号方位角的变化对阵列角度估计误差的影响比较小，阵列的指向性表现平稳，尤其当信噪比达到30 dB时，信号方位角的变化对阵列的角度估计误差没有影响。但是，当信噪比为5 dB时，阵列的角度估计误差随信号方位角的变化波动较为明显，因此在信噪比≤5 dB的低信噪比情况下，可通过绕阵列中心旋转的方式降低较低信噪比对信号角度估计误差的影响。

4 结 论

本文提出了一种改进的粒子群算法(IPSO算法)，该算法避免了传统算法易于过早收敛到局部解的问题。利用IPSO算法和LDWPSO算法分别对5臂 30阵元星形立体传声器阵列进行优化。由于改进算法采取分段优化的策略，通过降低粒子维数结合并行计算的优势，充分利用了惯性权重控制粒子搜索能力的性质，合理分配“粗”优化和 “精细”优化，所以在优化过程中不仅缩短了计算时间，而且得到了更优的结果。

通过主瓣宽度、旁瓣水平、信号源数和信噪比对两种阵列进行多方面比较，除主瓣宽度略宽外，根据本文提出的改进算法所设计的阵列在其余各方面都优于对比阵列。

最后讨论了空间角和信噪比对本文改进算法的阵列指向性的影响，得到了在不同信噪比下，信号以不同俯仰角和方位角入射时阵列的指向特性，发现当信噪比小于 10 dB时，阵列的角度误差较大，当信噪比大于等于20 dB时，阵列的角度误差较小。

参考文献

[1] CEN L, ZHU LY, SER W, et al. Linear aperiodic array synthesis using an improved genetic algorithm[J]. Antennas & Propagation IEEE Transactions on, 2012, 60(2): 895-902.

[2] JAIN R, MANI G S. Dynamic thinning of antenna array using geneic algorithm[J]. Progress in Electromagnetics Research B,2011, 32(32): 1-20.

[3] KHALID A, SHEIKH S A, SHAH I U H, et al. Synthesis of linear antenna array using genetic algorithm to reduce peak sidelobe level[C]//International Conference on Electrical & Electrics Engineering, 2015: 346-350.

[4] CHAN K Y, KWONG C K, LUO X G. Improved orthogonal array based simulated annealing for design optimization[J]. Expert Systems with Applications, 2009, 36(4): 7379-7389.

[5] CARDONE G, CINCOTTI G, PAPPALARDO M. Design of wide-band arrays for low side-lobe level beam patterns by simulated annealing[J]. IEEE Transactionson Ultrasonics Ferroelectri-cs& Frequencey Control, 2002, 49(8): 1050-1059.

[6] VERMA A, SANTOSH S. An improved array design for W-CMSR DOA estimation by simulated annealing[C]//Students Conference on Engineering & Systems, 2014: 1-5.

[7] RAJO-IGLESIAS E, QUEVEDO-TERUEL O. Array synthesis with diversity pattern using an ant colony algorithm[J]. IEEE International Symposiumon Antennas & Propagation, 2011:2433-2436.

[8] ZARE A. Application of ant colony optimization algorithm to pattern synthesis of uniform circular antenna array[J]. Applied Computational Electromagnetics Society Journal, 2015, 30(8):810-818.

[9] MANDAL D, BHATTACHARJEE A K, GHOSHAL S P. Linear antenna array synthesis using novel particle swarm optimization[C]//Kolkata, India: IEEE, 2011: 365-368.

[10] SONG J, ZHENG H, ZHANG L. Application of particle swarm optimization algorithm and genetic algorithms in beam broadening of phased array antenna[J]. Signals Systems & Electronics International Symposium on, 2010(1): 1-4.

[11] RECIOUI A. Sidelobe level reduction in linear array pattern synthesis using particle swarm optimization[J]. Journal of Optimization Theory and Applications, 2012, 153(2): 497-512.

[12] LI W T, SHI X W, HEI Y Q. An improved particle swarm optimization algorithm for pattern synthesis of phased arrays[J]. Progress In Electromagnetics Research, PIER82, 2008, 82(2): 319-332.