Broadening of cloud droplet size distributions and warm rain initiation associated with turbulence: an overview

LU Chun-Song, LIU Yn-Gng, NIU Sheng-Jie nd XUE Yu-Qi

aKey Laboratory of Meteorological Disaster, Ministry of Education (KLME)/Joint International Research Laboratory of Climate and Environment Change (ILCEC)/Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD)/Key Laboratory for Aerosol–Cloud–Precipitation of China Meteorological Administration, Nanjing University of Information Science & Technology, Nanjing, China;

bMinistry of Education Key Laboratory for Earth System Modeling, and Department for Earth System Science, Tsinghua University, Beijing, China;cEnvironmental and Climate Sciences Department, Brookhaven National Laboratory, Upton, NY, USA

1. Introduction

Warm rain refers to rain without the presence of the ice phase in clouds. Lau and Wu (2003) pointed out that warm rain accounts for 31% of the total rain amount and 72%of the total rain area in the tropics. Warm rain initiation affects the cloud life cycle and cloud macro- and microphysics. Since clouds in fluence radiation (Zhao and Ishizaka 2004; Xin and Li 2016; Fu and Lei 2017; Zhang and Chen 2017), parameterizations of warm rain initiation are important for evaluating cloud–radiation–climate feedbacks.Understanding warm rain initiation and cloud droplet size distribution broadening (spectral broadening hereafter) is one of the main challenges of cloud physics (Hu 1979; Beard and Ochs 1993; Sun et al. 2012; Blyth et al. 2013; Cooper,Lasher-Trapp, and Blyth 2013; Dagan, Koren, and Altaratz 2015; Selvam 2015; Seifert and Onishi 2016). First, some warm clouds are often observed to rain within a shorter time than theoretical expectations (Zhou and Gu 1963; McGraw and Liu 2004). Second, the theoretical cloud depth necessary to produce raindrops is greater than 2 km, but clouds with depths of less than 1 km have been observed to rain(Zhou and Gu 1963). Third, according to conventional condensation theory (Wallace and Hobbs 2006), cloud droplet size distributions are much narrower than those fromin situobservations (e.g. Lu, Niu et al. 2013). Fourth, it is still unclear how embryonic rains around 20 μm in radius form.

This review focuses on the effects of turbulence on the broadening of cloud droplet size distributions and warm rain initiation. Due to the space limit, other mechanisms,like the effects of giant cloud condensation nuclei (e.g.Feingold et al. 1999; Yin et al. 2000; Fang and Zheng 2011;Yang, Lei, and Zhang 2012; Guo, Fu et al. 2015), are not included in this review. Besides, many Chinese scientists have made contributions to this topic since the 1950s, but most of those studies were published in Chinese and are not readily accessible to the majority of the international communities in this field. So, a purpose of this review is to introduce these studies in English.

The rest of the paper is organized as follows: Section 2 presents the effects of fluctuations on condensation and collision–coalescence, including the progress of studies conducted in- and outside China. In Section 3, we address turbulent entrainment-mixing mechanisms, including their de finitions, methods (microphysics and dynamics),and parameterizations. In Section 4, we give a brief overview of the systems theory and its application. Concluding remarks are presented in Section 5.

2. Effects of turbulent fluctuations on condensation and collision–coalescence

2.1. Studies in China

Studies on cloud/fog and precipitation physics in China began in 1958 to meet the needs of weather modification(Gu 1963). As pointed out by Gu (1962), size distribution formation is not only a key topic in cloud/fog microphysics,but also critical in the examination of the effects of macro conditions on cloud/fog formation and development and the interactions between macro- and microphysical processes. Chinese scientists conductedin situobservations on Hengshan Mountain (27.25°N, 112.86°E) in Hunan Province and Taishan Mountain (36.18°N, 117.13°E) in Shandong Province. Xu (1964) designed an instrument to measure cloud/fog droplet size distributions. Air containing cloud/fog droplets was drawn by a fan through the instrument where droplets were impacted on sampling plates. Photos of the plates were taken continuously and each plate provided one droplet size distribution. It was found that the cloud droplet number concentration in stratocumulus clouds on Hengshan Mountain in September 1960 had fluctuation amplitudes in the range of 30%–100% and a fluctuation scale of 1–6 m over which the number concentration could be quite different. The cloud droplet size distributions also fluctuated and the fluctuation amplitude decreased with increasing sampling volume. Zhan, Chen, and Huang (1965) observed cloud droplet size distributions on Hengshan (April–May 1962)and Taishan (July–August 1962) Mountains. They realized that part of the fluctuations was due to small sampling volume and removed this part of the fluctuations from the total fluctuations in the observed data. They found that cloud droplet size distributions were broader for more significant fluctuations even when the average liquid water content was the same, suggesting that fluctuations in liquid water content were associated with spectral broadening. Number concentrations with different droplet sizes had different fluctuation strengths: large droplets had the largest fluctuations and medium-sized droplets had the smallest fluctuations. Another important characteristic of fluctuations of droplet size distributions was that the size distributions could be bimodal. Hong and Huang (1965)concluded that bimodal distributions were found more frequently with stronger rain intensity and intensity variation, which could be related to collision–coalescence. Zhu,Shi, and Huang (1965) found that bimodal distributions formed and disappeared gradually with the passage of a front. Lin and Gu (1965) examined the mechanism for the formation of the bimodal distribution and pointed out that turbulent collision–coalescence could be an important reason. Mao and Gu (1963) analyzed the observations on Hengshan Mountain and found that eight cases included super adiabatic liquid water content. Through theoretical analysis, they further revealed that when the vertical velocity decreased with increasing height, droplets would accumulate near the cloud base, which were responsible for the appearance of super adiabatic liquid water content.

In addition to observational studies, Chinese scientists also theoretically derived equations used to study the effects of fluctuations on spectral broadening. Gu (1962)derived and listed 20 equations in cloud/fog physics and discussed how fluctuations accelerated the condensation and collision–coalescence of droplets. Chinese scientists realized that many quantities in cloud/fog fluctuate (Jaw 1966), and the key studies are brie fly summarized here:

(1) Fluctuations of supersaturation. Zhou (1963)developed a stochastic theory for cloud droplet growth and a microphysical mechanism for precipitation in warm clouds. It was assumed that superstation fluctuations were in the form of a Gaussian distribution, and it was found that condensation with fluctuating supersaturation and turbulent electric collision–coalescence were both important for the formation of droplets in the range of 1–20 μm (radius). Similar conclusions were drawn in Xu, Li, and Wen (1966). Wen and Zhu (1987) investigated the condensation process under fluctuations of supersaturation in different clouds. For tropical warm clouds, the time needed for droplets to grow from 20 to 25 μm in radius was short, even with low fluctuations;for midlatitude warm clouds, the time was short only when fluctuations were strong.

(2) Fluctuations of number concentration and liquid water content. The growth of droplet size due to collision–coalescence between different droplets is closely related to the number concentration and liquid water content where collision–coalescence occurs. Assuming the cloud droplet size distribution was bimodal and the number concentration had fluctuations, Gu and Zhan(1962) found that collision–coalescence could produce droplets of 50 μm in radius or even larger than 100 μm. Wen (1964, 1966) and Xu, Li,and Wen (1966) found that fluctuations in liquid water content were feasible for the formation of large cloud droplets by collision–coalescence, no matter whether the fluctuation time/space scale was large or small.

(3) Fluctuations of vertical velocity. This type of fluctuation could affect how droplets move in clouds. Based on theoretical analysis, Xu and Gu (1963) found that droplets facing different vertical velocities would have different destinies and trajectories due to vertical velocity fluctuations. Some droplets were transported out of clouds rapidly, while others could cycle several times in clouds to produce large raindrops,which explained why shallow clouds with small cloud depths could produce rain. Xu (1963) further considered the effects of vertical velocity fluctuations and the vertical pro file of vertical velocity. Assuming the vertical velocity linearly decreased with increasing height, it was found that the cloud depth necessary for rain formation was smaller than that assuming that vertical velocity was distributed uniformly in the vertical direction.

(4) Cell structure. Cumulus clouds are often observed to be composed of convective cells (Xu and Li 1980). Xu and Li (1980) assumed that liquid water content and vertical velocity were larger inside cells than outside cells, i.e. fluctuations of both liquid water content and vertical velocity.Raindrops tended to appear with stronger fluctuations in cells, appearing in more cells and at larger cell scales. Li (1963) further examined the inhomogeneity of both vertical velocity and horizontal winds, in which cells transported cloud droplets back and forth in clouds. As a result,the cloud depth for precipitation formation decreased. Because of the importance of turbulent collision–coalescence, Xiao, Xu, and Huang(1988) included it in a one-dimensional cloud model, and simulations showed that turbulent collision–coalescence played a significant role in productions of big droplets.

In summary, by relating spectral broadening to various turbulent fluctuations, Chinese scientists and Russian scientists (Belyayev 1961; Levin and Sedunov 1966; Sedunov and Marlow 1975) were probably the first to introduce the idea of stochastic condensation into cloud physics (Liu,Daum, Chai and Liu 2002). Chinese scientists derived the equations that describe the collision–coalescence processes, accounting for fluctuations of key microphysical properties such as number concentration and liquid water content. These equations were promising for analytical study.

2.2. Studies outside China

Many studies have focused on stochastic condensation,attributing spectral broadening to turbulent fluctuations of supersaturation (Buikov 1961; Cooper 1989).Khvorostyanov and Curry (1999) revised the early equations of stochastic condensation by introducing two new features: (1) consideration of supersaturation as a non-conservative substance with differentiation between macroscale and microscale supersaturation; and (2) consideration of the supersaturation fluctuations of various frequencies. Shaw et al. (1998) presented a mechanism for the spectral broadening: cloud droplets were preferentially concentrated in regions of low vorticity in the turbulent flow field. Regions of high vorticity (low droplet concentration) developed higher supersaturation than regions of low vorticity (high droplet concentration). Droplets growing in regions of high vorticity experienced enhanced growth rates, allowing some droplets to grow larger than predicted by the classic theory of condensational growth. Vaillancourt et al. (2002) discussed the first direct numerical simulation (DNS) of the interaction between the turbulent flow field and cloud droplet growth by the diffusion of water vapor. It was found that, as a result of the increasing dissipation rate, fluctuations of supersaturation increased, but the width of the cloud droplet size distribution decreased. The result was a consequence of the decrease in the decorrelation time of supersaturation perturbations as the dissipation rate increased. This conclusion is different from those of many other studies. Celani et al. (2005) showed that the presence of an underlying turbulent velocity field induced a correlation between droplet trajectories and supersaturation, which led to both the enhancement of the droplet growth rate and to the fast spreading of the droplet size distribution. With DNS,Lanotte, Seminara, and Toschi (2009) found that spectral broadening increased with the Reynolds number of turbulence. Using a stochastic model and DNS, Sardina et al.(2015) found that the width of cloud droplet size distribution increased proportionally to the square root of time.Using a Brownian diffusion model, McGraw and Liu (2006)revealed the mechanisms of diffusive broadening of the droplet size distribution in a turbulent field and found that the stationary size distribution follows a Weibull distribution, consistent with the result from the systems theory,reviewed in Section 4.

Besides the effects of turbulence on stochastic condensation, turbulence also exerts several effects on droplet growth by collision–coalescence (Telford 1955; Shaw 2003), including increasing the droplet relative velocity(e.g. Arenberg 1939; Pinsky and Khain 1997; Wang, Wexler,and Zhou 1998), droplet clustering (e.g. Kostinski and Shaw 2001; Shaw, Kostinski, and Larsen 2002), increasing settling velocity (Dávila and Hunt 2001; Ayala et al. 2008), increasing collision efficiency/probability between droplets (e.g.Pinsky, Khain, and Shapiro 2000; Kunnen et al. 2013), etc.The four effects are explained as follows: The increased relative velocity is caused by the viscous drag and differential inertial response of the droplets to local fluid acceleration (Ayala et al. 2008). As mentioned above, droplet clustering means that inertial particles tend to accumulate in local regions of low vorticity and high strain rate due to an inertial bias (Maxey 1987; Shaw, Kostinski, and Larsen 2002). The average settling velocity of a small rigid spherical particle in homogeneous turbulence, subject to the Stokes drag force, has been shown to differ from that in still fluid (Maxey 1987; Wang and Maxey 1993). The collision efficiency is sensitive to the droplet relative velocity; so,in a cloud, the efficiency must account not only for differential sedimentation, but also for relative velocities due to turbulent acceleration (Pinsky, Khain, and Shapiro 1999).

Pinsky and Khain (2002) found that an increase in the collision kernel in turbulent surroundings was an important factor in the acceleration of large droplet and raindrop formation. Falkovich, Fouxon, and Stepanov (2002) derived a formula for the collision rate of small heavy particles in a turbulent flow and concluded that air turbulence could substantially accelerate the appearance of large droplets that trigger rain. Besides, DNS is becoming a useful tool to determine turbulent collision kernels, and the kernels from DNS have been widely used. For example, by solving the stochastic collection equation with the use of turbulent collision kernels, Franklin (2008) found that turbulence could significantly reduce the time to produce drizzle-sized drops. A similar conclusion was reached in Wyszogrodzki et al. (2013). Franklin (2014) further found that the amount of rainwater reaching the surface was six times larger in the simulation with the turbulent microphysics scheme.Grabowski and Wang (2008) de fined the turbulent speedup factor as the ratio of the rain initiation time for the turbulent collection kernel to the corresponding time for the gravitational kernel. They found that the factor was in the range of 0.75–0.85 and 0.60–0.75 for the different turbulent dissipation rates. Using a Lagrangian cloud model, Hoffmann, Noh, and Raasch (2017) found that raindrop formation easily occurred when turbulence-induced collision enhancement was considered, with or without any extra mechanisms of spectral broadening. Hsieh et al.(2009) evaluated eight autoconversion parameterizations against integration of the Kinetic Collection Equation and found that including turbulence effects on droplet collection increased autoconversion by factors of 1.82 and 1.24 for different clouds.

3. Turbulent entrainment-mixing mechanisms

Section 2 reviewed the turbulent effects in adiabatic clouds. Turbulence can affect cloud droplet size distributions through the entrainment of dry air into clouds and mixing between clouds and dry air. Stommel (1947) was the first scientist to realize the existence of entrainment of dry air into clouds; the cloud lapse rate was not wet-adiabatic, and the vertical gradient of liquid water content was different from that derived from adiabatic theory.Studies on entrainment-mixing include, at least, how dry air is entrained into clouds, how large the entrainment rate is, and how cloud droplets respond to entrained dry air(Devenish et al. 2012; Wood 2012; Cheng, Lu, and Liu 2015;Guo, Lu et al. 2015, 2017; Lu et al. 2016). This review only focuses on the last question.

Homogeneous/inhomogeneous entrainment-mixing mechanisms have been the most studied for entrainment-mixing investigation. Figure 1 shows the schematic diagram. The circles represent cloud droplets. After dry air is entrained into clouds, dry air and cloudy air will mix together due to turbulence, causing the evaporation of droplets. The two processes (mixing and evaporation)occur at the same time. The question is which process is faster–mixing or evaporation? The answer would be different for different clouds or even different stages in one cloud.

If mixing is much faster than evaporation, mixing occurs first and all the droplets are distributed throughout the area, including cloudy air and dry air. After mixing, all the droplets face the same saturation de ficit (relative humidity minus 100%) and evaporate at the same time, thus decreasing the droplet size. Number concentration also decreases because of dilution. So, droplet size and number concentration are positively correlated. This is termed the homogeneous entrainment-mixing mechanism, which was first studied by Warner (1973). It was found that if dry air was nucleus-free, mixing broadened the cloud droplet size distribution only slightly. If dry air contained nuclei,which were activated to produce droplets after mixing, the size distribution was broadened considerably but in a way that was not observed in natural clouds. In natural clouds,it was found that the dispersion of the size distribution was independent of the amount of mixing. Thus, from both theory and observation, it was concluded that homogeneous mixing between cloudy and dry air was unimportant in determining the size distribution, at least in the early stages of cloud growth. The discouraging results from Warner (1973) did not stop other scientists from using the concept of homogenous mixing. Mason and Jonas (1975),Lee and Pruppacher (1977), and Jonas and Mason (1982)all assumed homogeneous mixing and were able to reproduce the bimodal cloud droplet size distribution observed by Warner (1969). Recently, Yang, Shaw, and Xue (2016)showed that there was a critical height above the mixing level under the assumptions of a clean environment and homogeneous mixing, and super-adiabatic droplets existed above the critical height.

If evaporation is much faster than mixing, evaporation occurs first and the droplets closest to the dry air evaporate completely to saturate the dry air. After evaporation,mixing occurs. Because the dry air is already saturated,no droplets evaporate during mixing. As a result, the number concentration decreases significantly while the droplet size does not change. This is termed the extreme inhomogeneous entrainment-mixing mechanism. If after extreme inhomogeneous entrainment-mixing the diluted cloud parcel is lifted upward again, then the droplets in the diluted cloud parcel will grow faster than those in the adiabatic cloud. The reason is that the number concentration is lower, the surface area for condensation is smaller, and the supersaturation is larger in the diluted cloud parcel.It is expected that the droplet size and number concentration are negatively correlated. This is termed inhomogeneous mixing with subsequent ascent. The extreme inhomogeneous entrainment-mixing mechanism was first found by Latham and Reed (1977). They performed experiments in which droplets formed by condensation were drawn slowly down a cylindrical tube of length 5 m,and found that some droplets of all sizes were completely evaporated, while others were not significantly affected.Baker, Corbin, and Latham (1980) assumed extreme inhomogeneous entrainment-mixing mechanism in their model and found that a small proportion of droplets could grow several times faster than adiabatic theory predicted.The calculations produced spectral shapes that agreed well with those observed in cumulus clouds by Warner (1969).

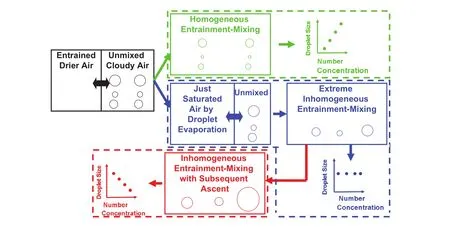
Figure 1. Schematic diagram of homogeneous/inhomogeneous entrainment-mixing mechanisms (e.g. Baker, Corbin, and Latham 1980;Yum 1998; Lu, Liu, and Niu 2011).Note: See text for explanations.

The above concept shows two extremes of entrainment-mixing mechanisms. The mechanisms in real clouds are much more complicated. Many scientists have been focusing on dissecting the real entrainment-mixing mechanisms in natural clouds, through theoretical analysis,in situobservations, and high-resolution simulations. Baker and Latham (1979), Baker, Corbin, and Latham (1980),and Baker et al. (1984) used two timescales to quantitatively describe the speeds of two processes, mixing and evaporation, i.e.τmandτr, respectively. The parameterτmis the time needed for dry air to be completely mixed andτris the response time between cloud droplets and dry air. The ratio of the two quantities, also known as the Damkohler number,τm/τr, has been widely used in entrainment-mixing studies (Burnet and Brenguier 2007; Jeffery 2007; Andrejczuk et al. 2009; Yum et al. 2015; Pinsky, Khain,and Korolev 2016; Yeom et al. 2017). Lehmann, Siebert,and Shaw (2009) realized that the dry eddy size used in the calculation ofτmwas often unknown. They de fined a transition length for the Damkohler number equal to one.Lu, Liu, and Niu (2011) and Kumar, Schumacher, and Shaw(2013) further calculated the ratio of the transition length to the Kolmogorov microscale; Lu, Liu, and Niu (2011)named it the transition scale number. A larger transition scale number indicates that mixing is more homogeneous. Besides these dynamical quantities, mixing diagrams of droplet size vs. number concentration or verus liquid water content were introduced (e.g. Pawlowska, Brenguier,and Burnet 2000; Burnet and Brenguier 2007; Gerber et al. 2008; Freud, Rosenfeld, and Kulkarni 2011; Lu, Liu, and Niu 2013; Small, Chuang, and Jonsson 2013; Tölle and Krueger 2014). Based on the de finitions of homogeneous/inhomogeneous mixing mechanisms described above, the dominant mechanism could be identified through aircraft observations (e.g. Lehmann, Siebert, and Shaw 2009) and numerical simulations (Andrejczuk et al. 2006; Krueger 2008; Kumar, Schumacher, and Shaw 2014; Gao et al.2017). Many observational studies have suggested that the entrainment-mixing process could be close to homogeneous (e.g. Jensen et al. 1985; Lu, Liu, and Niu 2014), extreme inhomogeneous (e.g. Freud, Rosenfeld, and Kulkarni 2011),or neither homogeneous nor extreme inhomogeneous(Lehmann, Siebert, and Shaw 2009; Lu, Liu et al. 2013).Usually, cloud droplet size distributions are measured by the Forward Scattering Spectrometer Probe, the Cloud and Aerosol Spectrometer, or similar instruments, which require averaging over long distances. Beals et al. (2015)overcame the large-scale spatial averaging problem by using an airborne digital in-line holographic system that imaged the three-dimensional structure within cloud volumes of ～15 cm3and provided size distributions. The measurements revealed that inhomogeneous mixing dominated, with sharp transitions between cloud and clear air properties, persisting to dissipative scales (＜1 cm).

To quantitatively describe how much mixing is homogeneous, the homogeneous mixing degree or similar quantities have been de fined (Gerber et al. 2008; Morrison and Grabowski 2008; Lu, Liu et al. 2013). Based onin situobservations and numerical simulations, parameterizations of entrainment-mixing mechanisms have been developed, which could be used to diagnose instantaneous entrainment-mixing mechanisms in models (Andrejczuk et al. 2009; Lu, Liu et al. 2013). Effects of different entrainment-mixing parameterizations on cloud microphysics have been tested. Grabowski (2006), Chosson, Brenguier,and Schüller (2007), and Slawinska et al. (2008) found that cloud microphysical properties were very sensitive to the entrainment-mixing parameterizations. However,Slawinska et al. (2012), Morrison and Grabowski (2008),and Hill, Feingold, and Jiang (2009) found that the effects of mixing on cloud microphysics were not as sensitive as those found by previous studies. Thus, this topic is still controversial.

There are several other ideas of entrainment-mixing mechanisms. In entity-type entrainment mixing (Telford and Chai 1980; Telford 1996), dry air is entrained above the cloud top and behaves as a continuing entity. One entity is like a parcel/cell in the clouds. During the descent of the entity, droplets evaporate completely to saturate the entity. Afterwards, the surrounding cloudy air is further mixed into the entity. The droplet size distribution in the entity is the same as that in the surrounding cloud, but the number concentration is lower. The entity goes up when buoyancy is restored. Due to the lower number concentration, droplets in the entity can grow larger than those in the adiabatic clouds. Thus, the number of recycling times of ‘entity’ in clouds is key to generating a broader size distribution and raindrops. A major challenge is how to determine the number of the recycling times, which may be related to turbulence intensity, thermodynamic conditions (e.g. temperature, relative humidity in dry air),and microphysical properties (e.g. liquid water content in clouds).

The idea of vertical circulation mixing (Wang et al. 2009;Yum et al. 2015) is similar. As the cloud parcel descends from the cloud top, cloud droplets evaporate until complete evaporation is reached. This height would be the local cloud base during the re-ascension of the parcels.If some of the descending parcels are more diluted than others, the local cloud base would have different heights.These parcels would mix together during ascension, which would broaden the cloud droplet size distributions. The idea of fluctuating cloud bases is similar to that proposed by Betts (1978, 1983), whereby they analyzed the different cloud bases for different parcels using saturation point diagrams.

Thus, despite decades of research, the effects of entrainment-mixing mechanisms on cloud microphysical properties and cloud droplet size distribution still remain elusive,full of uncertainty. Further studies are needed through theoretical analysis, observations, and numerical simulations.

4. Systems theory

As introduced above, clouds are turbulent and cloud microphysical properties fluctuate significantly; also, turbulent entrainment-mixing has significant effects on cloud droplet size distributions. In fact, turbulence-induced fluctuations and entrainment-mixing are closely intertwined,which makes it even more difficult to understand the formation of cloud droplet size distributions. Besides turbulent fluctuations and entrainment-mixing, there are many other factors affecting cloud droplet size distributions,e.g. aerosol. This complexity inspired Liu and his group to consider cloud droplets as a system, without concern for the details of each individual droplet affected by different factors (Liu 1995, 1997; Liu et al. 1995). After realizing that the molecular system and the atmospheric particle system are both multi-body and polydisperse systems with stochastic fluctuations, Liu et al. (1995) applied Shannon’s maximum entropy principle to the cloud droplet system to develop a systems theory. Shannon’s maximum entropy principle, as a theory for studying stochastic multi-body systems, has been successfully applied to various complex systems. If a stochastic system is governed by some restrictive conditions and characterized by a continuous random variableywith probability density functionρ(y),ρ(y) has many possible solutions, due to the fluctuations, andρ(y)corresponds to Shannon’s entropyH(y).Shannon’s maximum entropy principle indicates that whenH(y) reaches its maximum, its correspondingρ(y) will have the largest possibility of occurrence. The systems theory predicts that the most probable size distribution is a Weibull distribution. Liu (1995, 1997) further proposed a general framework to unify atmospheric particle systems, including the unification of atmospheric particle shapes into self-similar fractals and the generalization from self-similar to self-affine particles. Liu and Hallett (1997) further extended the systems theory for cloud droplet size distributions from clouds with conserved liquid water content to other cases,accounting for the degree of entrainment-mixing. From the generalized systems theory, a general ‘1/3’ power law was then formulated between the effective radius and the ratio of liquid water content to number concentration.

Besides the most probable size distribution, Liu and Hallett (1998) obtained the least probable distribution (a delta distribution) by studying the functional relationship between a cloud droplet size distribution and the corresponding energy change to form such a droplet population. The Weibull distribution is much wider than the delta distribution, but theoretical analysis in Liu, Daum,Chai, and Liu (2002) indicated that the Weibull distribution approached the delta distribution with decreasing fluctuations, because the width of the cloud droplet size distribution was closely related to fluctuation levels in clouds and increased with increasing fluctuations. Liu, Daum, and Hallett (2002) generalized the systems theory to allow for varying fluctuations. The theory indicates that there exists an important characteristic scale (saturation scale), below which droplet size distributions strongly depend on the scale over which they are sampled. However, beyond this scale, droplet size distributions do not change with further increases in the averaging scale. An important prediction of the systems theory is that the observed discrepancy between the observed and predicted droplet size distribution may lie in the scale mismatch: in turbulent clouds,the observed size distribution represents the average over large scales and, thus, is closer to the broader most probable size distribution, whereas the delta function, like a narrow distribution, corresponds to the least probable distribution that is hardly observed, even at small local scales. The systems theory also provides a theoretical basis for considering microphysical parameterizations for large scale models as a general issue of statistical physics (Liu,Daum, Chai, and Liu 2002).

A similar systems theory has been developed to explain the rain initiation by combining the systems theory for cloud droplet size distribution and nucleation theory(McGraw and Liu 2003, 2004). The theory treats rain formation as a barrier-crossing process and is used to derive a theoretical expression for the critical droplet radius that differentiates between cloud droplets and small raindrops(Liu, Daum, and McGraw 2004).

5. Concluding remarks

In this paper we review studies on spectral broadening and rain initiation and, because they were written in Chinese and are thus not accessible to most non-Chinese scientists, we pay special attention to early studies by Chinese scientists.

Chinese scientists carried out field campaigns over mountains to measure cloud droplet size distributions,using self-made instruments, in the 1950s and 1960s. They observed fluctuations of cloud microphysical properties and cloud droplet size distributions. They also observed bimodal distributions and super adiabatic liquid water content. Compared with observations, they focused more on the theoretical side of cloud physics, in which equations governing cloud physics were derived. Based on these equations, the effects of fluctuations on stochastic condensation and collision–coalescence were studied, including fluctuations of supersaturation, number concentration,liquid water content, vertical velocity, and existence of cell structures. Turbulent fluctuations were found to be important for spectral broadening. This topic has also been widely studied throughout the world. Particularly with high-resolution DNS simulations, many studies concluded that stochastic condensation in a turbulent environment contributed to spectral broadening, while opposite effects were found in others. Different from stochastic condensation, there is more consensus that turbulent fluctuations play significant roles in the collision–coalescence process because turbulence increases the droplet relative velocity,collision efficiency/probability between droplets, and settling velocity, as well as causes droplet clustering.

Besides turbulent fluctuations, turbulence also causes entrainment of dry air into clouds, and entrainment-mixing affects cloud microphysics. Several types of turbulent entrainment-mixing mechanisms are reviewed here, such as homogeneous/inhomogeneous entrainment-mixing,entity-type entrainment-mixing, and vertical circulation mixing. The mechanism most studied is the homogeneous/inhomogeneous mixing. Different dynamical quantities–Damkohler number, transition length, and transition scale number–were de fined to distinguish homogeneous and inhomogeneous mixing mechanisms. Mixing diagrams of droplet size vs. number concentration or liquid water content were introduced to identify different mixing mechanisms from the point of view of microphysics.Homogeneous mixing degrees were de fined to tell how much of mixing is homogeneous. How different mixing mechanisms affect cloud microphysics were tested in models.

As a theory for unifying turbulent fluctuations, entrainment-mixing, and other factors, systems theory provides a theoretical framework for explaining the shapes of cloud droplet size distributions. The theory predicts that the most probable size distribution is the Weibull distribution. The Weibull distribution approaches the delta distribution (least probable distribution) if turbulent fluctuations decrease. Cloud droplet size distributions are also scale-dependent; there is a saturation scale, over which the size distributions become stable.

Several challenges remain to be addressed. First, the detailed physical processes about the effects of fluctuations and entrainment-mixing on cloud droplet size distributions are still not clear, so more accurate and high-resolution observations, laboratory experiments,and high-resolution numerical simulations are needed.In addition, there is room for improvement in technologies for measuring temperature, water vapor, and vertical velocity. Recently, Siebert and Shaw (2017) studied supersaturation fluctuations during the early stages of cumulus formation. The Pi cloud chamber developed at the Michigan Technological University has shown its advantages in examining the interactions between supersaturation fluctuations and aerosol, and their effects on spectral broadening (Chandrakar et al. 2016, 2017; Chang et al. 2016). On the modeling front, models such as DNS(Gao et al. 2017), the Explicit Mixing Parcel Model (Tölle and Krueger 2014), and large-eddy simulation models, etc.,can be used to study the mechanisms of how fluctuations and entrainment-mixing affect cloud droplet size distributions and the scale dependence of the mechanisms (Lu,Liu, Niu, and Endo 2014). Second, the effects of turbulent fluctuations and entrainment-mixing processes have been unrealistically separated in most theoretical studies, with the possible exception of systems theory (Liu, Daum,Chai, and Liu 2002). However, current systems theory is largely descriptive, and thus further advancement into a predictive theory poses a challenge as well. Third, clouds play a significant role in weather forecasting and climate prediction. However, cloud parameterizations in models are far from complete. One critical problem hindering accurate parameterizations is the effects of fluctuations and entrainment-mixing on cloud physics. More development/improvement of parameterizations of fluctuations and entrainment-mixing, and testing in large-eddy simulations, cloud-resolving models, and even large-scale models, are necessary to see how the new parameterizations affect cloud/precipitation and radiation.

Disclosure statement

No potential conflict of interest was reported by the authors.

Funding

This research was supported by the National Key Research and Development Program of China [grant number 2017YFA060 4000], the China Meteorological Administration Special Public Welfare Research Fund [grant number GYHY201406001], the National Natural Science Foundation of China (NSFC) [grant number 91537108], the Natural Science Foundation of Jiangsu Province, China [grant number BK20160041], the U.S. Department of Energy’s BER Atmospheric System Research Program[grant number DE-SC00112704], the Six Talent Peak Project in Jiangsu, China [grant number 2015-JY-011], the 333 High-level Talents Training Project in Jiangsu [grant number BRA2016424],and the NSFC [grant number 41305120].

References

Andrejczuk, M., W. W. Grabowski, S. P. Malinowski, and P. K.Smolarkiewicz. 2006. “Numerical Simulation of Cloud-Clear Air Interfacial Mixing: Effects on Cloud Microphysics.”Journal of the Atmospheric Sciences63: 3204–3225. doi:10.1175/JAS3813.1.

Andrejczuk, M., W. W. Grabowski, S. P. Malinowski, and P. K.Smolarkiewicz. 2009. “Numerical Simulation of Cloud–Clear Air Interfacial Mixing: Homogeneous versus Inhomogeneous Mixing.”Journal of the Atmospheric Sciences66: 2493–2500.doi:10.1175/2009JAS2956.1.

Arenberg, D. 1939. “Turbulence as the Major Factor in the Growth of Cloud Drops.”Bulletin of the American Meteorological Society20: 444–448.

Ayala, O., B. Rosa, L. P. Wang, and W. W. Grabowski. 2008. “Effects of Turbulence on the Geometric Collision Rate of Sedimenting Droplets. Part 1. Results from Direct Numerical Simulation.”New Journal of Physics10: 75015–75031. doi:10.1088/1367-2630/10/7/075015.

Baker, M. B., R. E. Breidenthal, T. W. Choularton, and J. Latham.1984. “The Effects of Turbulent Mixing in Clouds.”Journal of the Atmospheric Sciences41: 299–304. doi:10.1175/1520-0469(1984)041＜0299:TEOTMI＞2.0.CO;2.

Baker, M. B., R. G. Corbin, and J. Latham. 1980. “The In fluence of Entrainment on the Evolution of Cloud Droplet Spectra:I. A Model of Inhomogeneous Mixing.”Quarterly Journal of the Royal Meteorological Society106: 581–598. doi:10.1002/qj.49710644914.

Baker, M. B., and J. Latham. 1979. “The Evolution of Droplet Spectra and the Rate of Production of Embryonic Raindrops in Small Cumulus Clouds.”Journal of the Atmospheric Sciences36: 1612–1615. doi:10.1175/1520-0469(1979)036＜1612:TEO DSA＞2.0.CO;2.

Beals, M. J., J. P. Fugal, R. A. Shaw, J. Lu, S. M. Spuler, and J. L.Stith. 2015. “Holographic Measurements of Inhomogeneous Cloud Mixing at the Centimeter Scale.”Science350: 87–90.doi:10.1126/science.aab0751.

Beard, K. V., and H. T. Ochs. 1993. “Warm-Rain Initiation:An Overview of Microphysical Mechanisms.”Journal of Applied Meteorology32: 608–625. doi:10.1175/1520-0450(1993)032＜0608:WRIAOO＞2.0.CO;2.

Belyayev, V. 1961. “On the Droplet Size Distribution in a Cloud at the Condensation Stage of Development.”IzvestiiAAkademii Nauk SSSR. SeriiA Geo fizickeskaiA8: 1209–1213.

Betts, A. 1978. “Convection in the Tropics.”Quarterly Journal of the Royal Meteorological Society Suppl: 105–132.

Betts, A. K. 1983. “Thermodynamics of Mixed Stratocumulus Layers: Saturation Point Budgets.”Journal of the Atmospheric Sciences40: 2655–2670. doi:10.1175/1520-0469(1983)040＜2655:TOMSLS＞2.0.CO;2.

Blyth, A. M., J. H. Lowenstein, Y. Huang, Z. Cui, S. Davies, and K.S. Carslaw. 2013. “The Production of Warm Rain in Shallow Maritime Cumulus Clouds.”Quarterly Journal of the Royal Meteorological Society139: 20–31. doi:10.1002/qj.1972.

Buikov, M. 1961. “Kinetics of Distillation in a Polydisperse Fog.”IzvestiiA Akademii Nauk SSSR. SeriiA GeofizickeskaiA7: 1058–1065.

Burnet, F., and J. L. Brenguier. 2007. “Observational Study of the Entrainment-Mixing Process in Warm Convective Clouds.”Journal of the Atmospheric Sciences64: 1995–2011.doi:10.1175/JAS3928.1.

Celani, A., G. Falkovich, A. Mazzino, and A. Seminara. 2005.“Droplet Condensation in Turbulent Flows.”Europhysics Letters70: 775–781. doi:10.1209/epl/i2005-10040-4.

Chandrakar, K. K., W. Cantrell, K. Chang, D. Ciochetto, D.Niedermeier, M. Ovchinnikov, R. A. Shaw, and F. Yang. 2016.“Aerosol Indirect Effect from Turbulence-Induced Broadening of Cloud-Droplet Size Distributions.”Proceedings of the National Academy of Sciences113: 14243–14248. doi:10.1073/pnas.1612686113.

Chandrakar, K. K., W. Cantrell, D. Ciochetto, S. Karki, G. Kinney, and R. Shaw. 2017. “Aerosol Removal and Cloud Collapse Accelerated by Supersaturation Fluctuations in Turbulence.”Geophysical Research Letters44: 4359–4367. doi:10.1002/2017GL072762.

Chang, K., J. Bench, M. Brege, W. Cantrell, K. Chandrakar, D.Ciochetto, C. Mazzoleni, L. R. Mazzoleni, D. Niedermeier,and R. A. Shaw. 2016. “A Laboratory Facility to Study Gas–Aerosol–Cloud Interactions in a Turbulent Environment: The Π Chamber.”Bulletin of the American Meteorological Society97: 2343–2358. doi:10.1175/BAMS-D-15-00203.1.

Cheng, M., C. Lu, and Y. Liu. 2015. “Variation in Entrainment Rate and Relationship with Cloud Microphysical Properties on the Scale of 5 M.”Science Bulletin60: 707–717. doi:10.1007/s11434-015-0737-8.

Chosson, F., J.-L. Brenguier, and L. Schüller. 2007. “Entrainment-Mixing and Radiative Transfer Simulation in Boundary Layer Clouds.”Journal of the Atmospheric Sciences64: 2670–2682.doi:10.1175/JAS3975.1.

Cooper, W. A. 1989. “Effects of Variable Droplet Growth Histories on Droplet Size Distributions. Part I: Theory.”Journal of the Atmospheric Sciences46: 1301–1311. doi:10.1175/1520-0469(1989)046＜1301:eovdgh＞2.0.co;2.

Cooper, W. A., S. G. Lasher-Trapp, and A. M. Blyth. 2013. “The In fluence of Entrainment and Mixing on the Initial Formation of Rain in a Warm Cumulus Cloud.”Journals of the Atmospheric Sciences70: 1727–1743. doi:10.1175/JAS-D-12-0128.1.

Dagan, G., I. Koren, and O. Altaratz. 2015. “Aerosol Effects on the Timing of Warm Rain Processes.”Geophysical Research Letters42: 4590–4598. doi:10.1002/2015GL063839.

Dávila, J., and J. C. R. Hunt. 2001. “Settling of Small Particles near Vortices and in Turbulence.”Journal of Fluid Mechanics440:117–145.

Devenish, B. J., P. Bartello, J. L. Brenguier, L. R. Collins, W. W.Grabowski, R. H. A. Ijzermans, S. P. Malinowski, et al. 2012.“Droplet Growth in Warm Turbulent Clouds.”Quarterly Journal of the Royal Meteorological Society138: 1401–1429.doi:10.1002/qj.1897.

Gerber, H. E., G. M. Frick, J. B. Jensen, and J. G. Hudson. 2008.“Entrainment, Mixing, and Microphysics in Trade-Wind Cumulus.”Journal of the Meteorological Society of Japan86A:87–106. doi:10.2151/jmsj.86A.87.

Falkovich, G., A. Fouxon, and M. G. Stepanov. 2002. “Acceleration of Rain Initiation by Cloud Turbulence.”Nature419: 151–154.doi:10.1038/nature00983.

Fang, W., and G. Zheng. 2011. “The Effect of Giant Cloud Condensation Nuclei on Warm-Cloud Precipitation.”Chinese Journal of Atmospheric Sciences35: 938–944 (in Chinese).

Feingold, G., W. R. Cotton, S. M. Kreidenweis, and J. T. Davis.1999. “The Impact of Giant Cloud Condensation Nuclei on Drizzle Formation in Stratocumulus: Implications for Cloud Radiative Properties.”Journal of the Atmospheric Sciences56:4100–4117. doi:10.1175/1520-0469(1999)056＜4100:TIOGCC＞2.0.CO;2.

Franklin, C. N. 2008. “A Warm Rain Microphysics Parameterization That Includes the Effect of Turbulence.”Journal of the Atmospheric Sciences65: 1795–1816.doi:10.1175/2007jas2556.1.

Franklin, C. N. 2014. “The Effects of Turbulent Collision–Coalescence on Precipitation Formation and Precipitation-Dynamical Feedbacks in Simulations of Stratocumulus and Shallow Cumulus Convection.”Atmospheric Chemistry and Physics14: 6557–6570. doi:10.5194/acp-14-6557-2014.

Freud, E., D. Rosenfeld, and J. R. Kulkarni. 2011. “Resolving Both Entrainment-Mixing and Number of Activated CCN in Deep Convective Clouds.”Atmospheric Chemistry and Physics11:12887–12900. doi:10.5194/acp-11-12887-2011.

Fu, Y., and H.-C. Lei. 2017. “Aircraft Observation of Cloud Microphysical Characteristics of Pre-Stratiform-Cloud Precipitation in Jiangxi Province.”Atmospheric and Oceanic Science Letters10: 364–371. doi:10.1080/16742834.2017.134 4090.

Gao, Z., Y. Liu, X. Li, and C. Lu. 2017. “A New Particle-Resolved Direct Numerical Simulation Model for Studying Turbulent Entrainment-Mixing Processes.”Journal of Geophysical Research, Submitted.

Grabowski, W. W. 2006. “Indirect Impact of Atmospheric Aerosols in Idealized Simulations of Convective-Radiative Quasi Equilibrium.”Journal of Climate19: 4664–4682. doi:10.1175/JCLI3857.1.

Grabowski, W. W., and L. P. Wang. 2008. “Diffusional and Accretional Growth of Water Drops in a Rising Adiabatic Parcel: Effects of the Turbulent Collision Kernel.”Atmospheric Chemistry & Physics Discussions8: 2335–2353. doi:10.5194/acpd-8-14717-2008.

Gu, Z. 1962. “Recent Investigations in the Theory of the Formation of the Cloud-Drop Spectra.”Acta Meteorologica Sinica32: 267–284 (in Chinese).

Gu, Z., ed. 1963.Some Theoretical Questions in Cloud/Fog Precipitation Microphysics. Beijing: Science Press (in Chinese).Gu, Z., and L. Zhan. 1962. “On the Growth of the Droplets under Gravitational Coalescence in a Fluctuating Environment.”Acta Meteorologica Sinica32: 301–307 (in Chinese).

Guo, X., D. Fu, X. Li, Z. Hu, H. Lei, H. Xiao, and Y. Hong. 2015.“Advances in Cloud Physics and Weather Modification in China.”Advances in Atmospheric Sciences32: 230–249.doi:10.1007/s00376-014-0006-9.

Guo, X., C. Lu, T. Zhao, Y. Liu, G. J. Zhang, and S. Luo. 2017.“Observational Study of the Relationship between Entrainment Rate and Relative Dispersion in Deep Convective Clouds.”Atmospheric Research.Advance Online Publication.doi:10.1016/j.atmosres.2017.09.013.

Guo, X., C. Lu, T. Zhao, G. Zhang, and Y. Liu. 2015. “An Observational Study of Entrainment Rate in Deep Convection.”Atmosphere6: 1362–1376. doi:10.3390/atmos6091362.

Hill, A. A., G. Feingold, and H. Jiang. 2009. “The In fluence of Entrainment and Mixing Assumption on Aerosol-Cloud Interactions in Marine Stratocumulus.”Journal of the Atmospheric Sciences66: 1450–1464.doi:10.1175/2008JAS2909.1.

Hoffmann, F., Y. Noh, and S. Raasch. 2017. “The Route to Raindrop Formation in a Shallow Cumulus Cloud Simulated by a Lagrangian Cloud Model.”Journal of the Atmospheric Sciences74: 2125–2142. doi:10.1175/jas-d-16-0220.1.

Hong, Z., and M. Huang, eds. 1965. “The Secondary Peak of Cloud Spectra and Other Important Characteristics on the Hengshan Mountain.” InStudies on Cloud/Fog Precipitation Microphysics in China, edited by Z. Gu, 98. Beijing: Science Press (in Chinese).

Hsieh, W. C., H. Jonsson, L. P. Wang, G. Buzorius, R. C. Flagan,J. H. Seinfeld, and A. Nenes. 2009. “On the Representation of Droplet Coalescence and Autoconversion: Evaluation Using Ambient Cloud Droplet Size Distributions.”Journal of Geophysical Research: Atmospheres114: D07201.doi:10.1029/2008JD010502.

Hu, Z. 1979. “On the Conditions of Warm Rain Formation in Cumulus Clouds.”Acta Meteorologica Sinica37: 72–79.

Jaw, J.-J. 1966. “Statistical Theory of Precipitation Process.”Tellus18: 722–730. doi:10.1111/j.2153-3490.1966.tb00293.x.

Jeffery, C. A. 2007. “Inhomogeneous Cloud Evaporation,Invariance, and Damköhler Number.”Journal of Geophysical Research112: D24S21. doi:10.1029/2007jd008789.

Jensen, J. B., P. H. Austin, M. B. Baker, and A. M. Blyth. 1985.“Turbulent Mixing, Spectral Evolution and Dynamics in a Warm Cumulus Cloud.”Journal of the Atmospheric Sciences42: 173–192. doi:10.1175/1520-0469(1985)042＜0173:TMSEA D＞2.0.CO;2.

Jonas, P. R., and B. J. Mason. 1982. “Entrainment and the Droplet Spectrum in Cumulus Clouds.”Quarterly Journal of the Royal Meteorological Society108: 857–869. doi:10.1002/qj.49710845808.

Khvorostyanov, V. I., and J. A. Curry. 1999. “Toward the Theory of Stochastic Condensation in Clouds. Part I: A General Kinetic Equation.”Journal of the Atmospheric Sciences56: 3985–3996.doi:10.1175/1520-0469(1999)056＜3985:tttosc＞2.0.co;2.

Kostinski, A. B., and R. A. Shaw. 2001. “Scale-Dependent Droplet Clustering in Turbulent Clouds.”Journal of Fluid Mechanics434: 389–398.

Krueger, S. K. 2008. “Fine-Scale Modeling of Entrainment and Mixing of Cloudy and Clear Air.” Paper Presented at the 15th International Conference on Clouds and Precipitation,Cancun, Mexico.

Kumar, B., J. Schumacher, and R. Shaw. 2013. “Cloud Microphysical Effects of Turbulent Mixing and Entrainment.”Theoretical and Computational Fluid Dynamics27: 361–376.doi:10.1007/s00162-012-0272-z.

Kumar, B., J. Schumacher, and R. A. Shaw. 2014. “Lagrangian Mixing Dynamics at the Cloudy-Clear Air Interface.”Journal of the Atmospheric Sciences71: 2564–2580. doi:10.1175/JAS-D-13-0294.1.

Kunnen, R. P. J., C. Siewert, M. Meinke, W. Schröder, and K. D.Beheng. 2013. “Numerically Determined Geometric Collision Kernels in Spatially Evolving Isotropic Turbulence Relevant for Droplets in Clouds.”Atmospheric Research127: 8–21.doi:10.1016/j.atmosres.2013.02.003.

Lanotte, A. S., A. Seminara, and F. Toschi. 2009. “Cloud Droplet Growth by Condensation in Homogeneous Isotropic Turbulence.”Journal of the Atmospheric Sciences66: 1685–1697. doi:10.1175/2008JAS2864.1.

Latham, J., and R. L. Reed. 1977. “Laboratory Studies of the Effects of Mixing on the Evolution of Cloud Droplet Spectra.”Quarterly Journal of the Royal Meteorological Society103: 297–306. doi:10.1002/qj.49710343607.

Lau, K. M., and H. T. Wu. 2003. “Warm Rain Processes over Tropical Oceans and Climate Implications.”Geophysical Research Letters30: 2290. doi:10.1029/2003GL018567.

Lee, I.-Y., and H. R. Pruppacher. 1977. “A Comparative Study on the Growth of Cloud Drops by Condensation Using an Air Parcel Model with and without Entrainment.”Pure and Applied Geophysics115: 523–545. doi:10.1007/BF00876119.

Lehmann, K., H. Siebert, and R. A. Shaw. 2009. “Homogeneous and Inhomogeneous Mixing in Cumulus Clouds: Dependence on Local Turbulence Structure.”Journal of the Atmospheric Sciences66: 3641–3659. doi:10.1175/2009JAS3012.1.

Levin, L., and Y. Sedunov. 1966. “Stochastic Condensation of Drops and Kinetics of Cloud Spectrum Formation.”Journal De Recherches Atmospheriques2: 425–432.

Li, M. 1963. “Effects of Convective Cells in Clouds on Precipitation Microphysical Processes.” InSome Theoretical Questions in Cloud/Fog Precipitation Microphysics, edited by Z. Gu, 59.Beijing: Science Press (in Chinese).

Lin, H., and Z. Gu. 1965. “Preliminary Explanations on the Secondary Peak Formation in the Cloud Droplet Spectra.”Science Bulletin10: 923–925 (in Chinese).

Liu, Y. 1995. “On the Generalized Theory of Atmospheric Particle Systems.”Advances in Atmospheric Sciences12: 419–438.doi:10.1007/BF02657003.

Liu, Y. 1997. “On the Unified Theory of Atmospheric Particle Systems Part Ii: Self-Affine Particles.”Advances in Atmospheric Sciences14: 369–388. doi:10.1007/s00376-997-0057-2.

Liu, Y., P. H. Daum, S. K. Chai, and F. Liu. 2002. “Cloud Parameterizations, Cloud Physics, and Their Connections: An Overview.”Recent Research in Developments in Geophysics4:119–142.

Liu, Y., P. H. Daum, and J. Hallett. 2002. “A Generalized Systems Theory for the Effect of Varying Fluctuations on Cloud Droplet Size Distributions.”Journal of the Atmospheric Sciences59:2279–2290. doi:10.1175/1520-0469(2002)059＜2279:AGSTFT＞2.0.CO;2.

Liu, Y., P. H. Daum, and R. McGraw. 2004. “An Analytical Expression for Predicting the Critical Radius in the Autoconversion Parameterization.”Geophysical Research Letters31: L06121.doi:10.1029/2003gl019117.

Liu, Y., and J. Hallett. 1997. “The ‘1/3’ Power Law between Effective Radius and Liquid-Water Content.”Quarterly Journal of the Royal Meteorological Society123: 1789–1795. doi:10.1002/qj.49712354220.

Liu, Y., and J. Hallett. 1998. “On Size Distributions of Cloud Droplets Growing by Condensation: A New Conceptual Model.”Journal of the Atmospheric Sciences55: 527–536.doi:10.1175/1520-0469(1998)055＜0527:OSDOCD＞2.0.CO;2.

Liu, Y., L. You, W. Yang, and F. Liu. 1995. “On the Size Distribution of Cloud Droplets.”Atmospheric Research35: 201–216.doi:10.1016/0169-8095(94)00019-A.

Lu, C., Y. Liu, and S. Niu. 2011. “Examination of Turbulent Entrainment-Mixing Mechanisms Using a Combined Approach.”Journal of Geophysical Research116: D20207.doi:10.1029/2011JD015944.

Lu, C., Y. Liu, and S. Niu. 2013. “A Method for Distinguishing and Linking Turbulent Entrainment Mixing and Collision-Coalescence in Stratocumulus Clouds.”Chinese Science Bulletin58: 545–551. doi:10.1007/s11434-012-5556-6.

Lu, C., Y. Liu, and S. Niu. 2014. “Entrainment-Mixing Parameterization in Shallow Cumuli and Effects of Secondary Mixing Events.”Chinese Science Bulletin59: 896–903.doi:10.1007/s11434-013-0097-1.

Lu, C., Y. Liu, S. Niu, and S. Endo. 2014. “Scale Dependence of Entrainment-Mixing Mechanisms in Cumulus Clouds.”Journal of Geophysical Research119: 13877–13890.doi:10.1002/2014JD022265.

Lu, C., Y. Liu, S. Niu, S. K. Krueger, and T. Wagner. 2013. “Exploring Parameterization for Turbulent Entrainment-Mixing Processes in Clouds.”Journal of Geophysical Research118:185–194. doi:10.1029/2012JD018464.

Lu, C., Y. Liu, G. J. Zhang, X. Wu, S. Endo, L. Cao, Y. Li, and X. Guo.2016. “Improving Parameterization of Entrainment Rate for Shallow Convection with Aircraft Measurements and Large Eddy Simulation.”Journal of the Atmospheric Sciences73: 761–773. doi:10.1175/JAS-D-15-0050.1.

Lu, C., S. Niu, Y. Liu, and A. M. Vogelmann. 2013. “Empirical Relationship between Entrainment Rate and Microphysics in Cumulus Clouds.”Geophysical Research Letters40: 2333–2338.doi:10.1002/grl.50445.

Mao, J., and Z. Gu. 1963. “Formation of Super Adiabatic Liquid Water Content in the Stratocumulus Liquid Water Content Distribution.” InSome Theoretical Questions in Cloud/Fog Precipitation Microphysics, edited by Z. Gu, 59. Beijing: Science Press (in Chinese).

Mason, B. J., and P. R. Jonas. 1975. “The Evolution of Droplet Spectra and Large Droplets by Condensation in Cumulus Clouds.”Quarterly Journal of the Royal Meteorological Society101: 397–397. doi:10.1002/qj.49710142828.

Maxey, M. R. 1987. “The Gravitational Settling of Aerosol Particles in Homogeneous Turbulence and Random Flow Fields.”Journal of Fluid Mechanics174: 441–465. doi:10.1017/S0022112087000193.

McGraw, R., and Y. Liu. 2003. “Kinetic Potential and Barrier Crossing:A Model for Warm Cloud Drizzle Formation.”Physical Review Letters90: 018501. doi:10.1103/PhysRevLett.90.018501.

McGraw, R., and Y. Liu. 2004. “Analytic Formulation and Parametrization of the Kinetic Potential Theory for Drizzle Formation.”Physical Review E70: 031606. doi:10.1103/PhysRevE.70.031606.

McGraw, R., and Y. Liu. 2006. “Brownian Drift-Diffusion Model for Evolution of Droplet Size Distributions in Turbulent Clouds.”Geophysical Research Letters33: L03802.doi:10.1029/2005gl023545.

Morrison, H., and W. W. Grabowski. 2008. “Modeling Supersaturation and Subgrid-Scale Mixing with Two-Moment Bulk Warm Microphysics.”Journal of the Atmospheric Sciences65: 792–812. doi:10.1175/2007JAS2374.1.

Pawlowska, H., J. L. Brenguier, and F. Burnet. 2000. “Microphysical Properties of Stratocumulus Clouds.”Atmospheric Research55: 15–33. doi:10.1016/S0169-8095(00)00054-5.

Pinsky, M. B., and A. P. Khain. 1997. “Turbulence Effects on Droplet Growth and Size Distribution in Clouds – A Review.”Journal of Aerosol Science28: 1177–1214. doi:10.1016/S0021-8502(97)00005-0.

Pinsky, M. B., and A. P. Khain. 2002. “Effects of in-Cloud Nucleation and Turbulence on Droplet Spectrum Formation in Cumulus Clouds.”Quarterly Journal of the Royal Meteorological Society128: 501–533. doi:10.1256/003590002321042072.

Pinsky, M., A. Khain, and A. Korolev. 2016. “Theoretical Analysis of Mixing in Liquid Clouds – Part 3: Inhomogeneous Mixing.”Atmospheric Chemistry and Physics16: 9273–9297.doi:10.5194/acpd-15-30321-2015.

Pinsky, M., A. Khain, and M. Shapiro. 1999. “Collisions of Small Drops in a Turbulent Flow. Part I: Collision Efficiency.Problem Formulation and Preliminary Results.”Journal of the Atmospheric Sciences56: 2585–2600. doi:10.1175/1520-0469(2004)061＜1926:COSDIA＞2.0.CO;2.

Pinsky, M., A. Khain, and M. Shapiro. 2000. “Stochastic Effects of Cloud Droplet Hydrodynamic Interaction in a Turbulent Flow.”Atmospheric Research53: 131–169. doi:10.1016/S0169-8095(99)00048-4.

Sardina, G., F. Picano, L. Brandt, and R. Caballero. 2015.“Continuous Growth of Droplet Size Variance due to Condensation in Turbulent Clouds.”Physical Review Letters115: 184501. doi:10.1103/PhysRevLett.115.184501.

Sedunov, Y. S., and W. H. Marlow. 1975. “Physics of Drop Formation in the Atmosphere.”Physics Today28: 56–56.doi:10.1063/1.3068968.

Seifert, A., and R. Onishi. 2016. “Turbulence Effects on Warm-Rain Formation in Precipitating Shallow Convection Revisited.”Atmospheric Chemistry & Physics16: 12127–12141.

Selvam, A. M. 2015. “Rain Formation in Warm Clouds.” New York:Springer. doi:10.1007/978-3-319-13269-3.

Shaw, R. A. 2003. “Particle-Turbulence Interactions in Atmospheric Clouds.”Annual Review of Fluid Mechanics35:183–227. doi:10.1146/annurev. fluid.35.101101.161125.

Shaw, R. A., A. B. Kostinski, and M. L. Larsen. 2002. “Towards Quantifying Droplet Clustering in Clouds.”Quarterly Journal of the Royal Meteorological Society128: 1043–1057.doi:10.1256/003590002320373193.

Shaw, R. A., W. C. Reade, L. R. Collins, and J. Verlinde. 1998.“Preferential Concentration of Cloud Droplets by Turbulence:Effects on the Early Evolution of Cumulus Cloud Droplet Spectra.”Journal of the Atmospheric Sciences55: 1965–1976.doi:10.1175/1520-0469(1998)055＜1965:PCOCDB＞2.0.CO;2.

Siebert, H., and R. A. Shaw. 2017. “Supersaturation Fluctuations during the Early Stage of Cumulus Formation.”Journal of the Atmospheric Sciences74: 975–988. doi:10.1175/JAS-D-16-0115.1.

Slawinska, J., W. W. Grabowski, H. Pawlowska, and H. Morrison.2012.“Droplet Activation and Mixing in Large-Eddy Simulation of a Shallow Cumulus Field.”Journal of the Atmospheric Sciences69: 444–462. doi:10.1175/JAS-D-11-054.1.

Slawinska, J., W. W. Grabowski, H. Pawlowska, and A. A.Wyszogrodzki. 2008. “Optical Properties of Shallow Convective Clouds Diagnosed from a Bulk-Microphysics Large-Eddy Simulation.”Journal of Climate21: 1639–1647.doi:10.1175/2007JCLI1820.1.

Small, J. D., P. Chuang, and H. Jonsson. 2013. “Microphysical Imprint of Entrainment in Warm Cumulus.”Tellus B65: 6647–6662. doi:10.3402/tellusb.v65i0.19922.

Stommel, H. 1947. “Entrainment of Air into a Cumulus Cloud.”Journal of Meteorology4: 91–94. doi:10.1175/1520-0469(1947)004＜0091:EOAIAC＞2.0.CO;2.

Sun, J., H. Leighton, M. K. Yau, and P. Ariya. 2012. “Numerical Evidence for Cloud Droplet Nucleation at the Cloud-Environment Interface.”Atmospheric Chemistry and Physics12: 12155–12164. doi:10.5194/acp-12-12155-2012.

Telford, J. W. 1955. “A New Aspect of Coalescence Theory.”Journal of Meteorology12: 436–444. doi:10.1175/1520-0469(1955)012＜0436:anaoct＞2.0.co;2.

Telford, J. W. 1996. “Clouds with Turbulence; the Role of Entrainment.”Atmospheric Research40: 261–282.doi:10.1016/0169-8095(95)00038-0.

Telford, J. W., and S. K. Chai. 1980. “A New Aspect of Condensation Theory.”Pure and Applied Geophysics118: 720–742.doi:10.1007/BF01593025.

Tölle, M. H., and S. K. Krueger. 2014. “Effects of Entrainment and Mixing on Droplet Size Distributions in Warm Cumulus Clouds.”Journal of Advances in Modeling Earth Systems6: 281–299. doi:10.1002/2012MS000209.

Vaillancourt, P. A., M. K. Yau, P. Bartello, and W. W. Grabowski.2002. “Microscopic Approach to Cloud Droplet Growth by Condensation. Part II: Turbulence, Clustering, and Condensational Growth.”Journal of the Atmospheric Sciences59: 3421–3435. doi:10.1175/1520-0469(2002)059＜3421:MAT CDG＞2.0.CO;2.

Wallace, J., and P. Hobbs. 2006.Atmospheric Science: An Introductory Survey. San Diego, CA: Academic Press.

Wang, J., P. H. Daum, S. S. Yum, Y. Liu, G. I. Senum, M.-L. Lu, J.H. Seinfeld, and H. Jonsson. 2009. “Observations of Marine Stratocumulus Microphysics and Implications for Processes Controlling Droplet Spectra: Results from the Marine Stratus/Stratocumulus Experiment.”Journal of Geophysical Research114: D18210. doi:10.1029/2008jd011035.

Wang, L. P., and M. R. Maxey. 1993. “Settling Velocity and Concentration Distribution of Heavy Particles in Homogeneous Isotropic Turbulence.”Journal of Fluid Mechanics256: 27–68. doi:10.1017/S0022112093002708.

Wang, L., A. S. Wexler, and Y. Zhou. 1998. “Statistical Mechanical Descriptions of Turbulent Coagulation.”Physics of Fluids10:2647–2651. doi:10.1063/1.869777.

Warner, J. 1969. “The Microstructure of Cumulus Cloud. Part I. General Features of the Droplet Spectrum.”Journal of the Atmospheric Sciences26: 1049–1059. doi:10.1175/1520-0469(1969)026＜1049:TMOCCP＞2.0.CO;2.

Warner, J. 1973. “The Microstructure of Cumulus Cloud: Part IV.the Effect on the Droplet Spectrum of Mixing between Cloud and Environment.”Journal of the Atmospheric Sciences30:256–261. doi:10.1175/1520-0469(1973)030＜0256:TMOCCP＞2.0.CO;2.

Wen, C. 1964. “The Effects of Correlation Time of Fluctuations on Droplet Stochastic Growth.”Acta Meteorologica Sinica34:369–377 (in Chinese).

Wen, C. 1966. “Cloud Droplet Stochastic Growth with Large-Scale Fluctuations.”Acta Meteorologica Sinica36: 280–282 (in Chinese).

Wen, J., and Z. Zhu. 1987. “The Effects of the Fluctuating Condensation of Markov Type and the Single Discontinuous Gravitational Coagulation on Closing the Growth Gap of Droplets in Convective Warm Clouds.”Scientia Meteorologica Sinica55: 50–55 (in Chinese).

Wood, R. 2012. “Review: Stratocumulus Clouds.”Monthly Weather Review140: 2373–2423. doi:10.1175/MWR-D-11-00121.1.

Wyszogrodzki, A. A., W. W. Grabowski, L.-P. Wang, and O. Ayala.2013. “Turbulent Collision-Coalescence in Maritime Shallow Convection.”Atmospheric Chemistry and Physics13: 8471–8487. doi:10.5194/acpd-13-9217-2013.

Xiao, H., H. Xu, and M. Huang. 1988. “Numerical Simulations of Cloud Droplet Size Distribution Formations in Cumulus.Part 2: Roles of Collision-Coalescence and Atmospheric Stratification.”Scientia Atmospherica Sinica12: 312–319 (in Chinese).

Xin, J., and X.-F. Li. 2016. “Precipitation Responses to Radiative Processes of Water- and Ice-Clouds: An Equilibrium Cloud-Resolving Modeling Study.”Atmospheric and Oceanic Science Letters9: 306–314. doi:10.1080/16742834.2016.1191938.

Xu, H. 1963. “Further Analysis on Precipitation in Shallow Warm Clouds with Vertical Velocity Fluctuations.” InSome Theoretical Questions in Cloud/Fog Precipitation Microphysics, edited by Z.Gu, 59. Beijing: Science Press (in Chinese).

Xu, H. 1964. “Preliminary Observations of Fluctuations of Cloud/Fog Microphysics on the Hengshan Mountain.”Acta Meteorologica Sinica34: 539–547 (in Chinese).

Xu, H., and Z. Gu. 1963. “On the Formation of the Precipitation Element in a Shallow Warm-Cloud.”Acta Meteorologica Sinica33: 108–114 (in Chinese).

Xu, H., and G. Li. 1980. “A Study on the Formation of the Precipitation in Convective Cloud with Cell Structure.”Acta Meteorologica Sinica38: 260–268 (in Chinese).

Xu, Q., G. Li, and J. Wen. 1966. “Markov Process for Cloud Droplet Continuous Growth with Small-Scale Fluctuations and Its Roles in the Development of Cumulonimbus.”Acta Meteorologica Sinica36: 243–248 (in Chinese).

Yang, J., H. Lei, and Y. Zhang. 2012. “Numerical Simulation of the Impact of Giant Cloud Nuclei on Cloud Droplet Activation.”Climatic and Environmental Research17: 789–796.doi:10.3878/j.issn.1006-9585.2012.06.16 (in Chinese).

Yang, F., R. Shaw, and H. Xue. 2016. “Conditions for Super-Adiabatic Droplet Growth after Entrainment Mixing.”Atmospheric Chemistry and Physics16: 9421–9433.doi:10.5194/acp-16-9421-2016.

Yeom, J. M., S. S. Yum, Y. Liu, and C. Lu. 2017. “A Study on the Entrainment and Mixing Process in the Continental Stratocumulus Clouds Measured during the RACORO Campaign.”Atmospheric Research194: 89–99. doi:10.1016/j.atmosres.2017.04.028.

Yin, Y., Z. Levin, T. G. Reisin, and S. Tzivion. 2000. “The Effects of Giant Cloud Condensation Nuclei on the Development of Precipitation in Convective Clouds – A Numerical Study.”Atmospheric Research53: 91–116. doi:10.1016/S0169-8095(99)00046-0.

Yum, S. 1998.Cloud Droplet Spectral Broadening in Warm Clouds:An Observational and Model Study. PhD diss., University of Nevada, Reno, NV, USA.

Yum, S. S., J. Wang, Y. Liu, G. Senum, S. Springston, R. McGraw,and J. M. Yeom. 2015. “Cloud Microphysical Relationships and Their Implication on Entrainment and Mixing Mechanism for the Stratocumulus Clouds Measured during the Vocals Project.”Journal of Geophysical Research120: 5047–5069.doi:10.1002/2014JD022802.

Zhan, L., W. Chen, and M. Huang. 1965. “Preliminary Analysis on the Fluctuation Data of Cloud Microphysics on the Hengshan and Taishan Mountains.” InStudies on Cloud/Fog Precipitation Microphysics in China, edited by Z. Gu, 98. Beijing: Science Press (in Chinese).

Zhang, J.-Q., and H.-B. Chen. 2017. “Macrophysical Properties of Specific Cloud Types from Radiosonde and Surface Active Remote Sensing Measurements over the ARM Southern Great Plains Site.”Atmospheric and Oceanic Science Letters10:29–35. doi:10.1080/16742834.2017.1239505.

Zhao, C., and Y. Ishizaka. 2004. “Modeling Marine Stratocumulus with a Detailed Microphysical Scheme.”Advances in Atmospheric Sciences21: 61–74. doi:10.1007/BF03342546.

Zhou, X. 1963. “Statistical Theory for Microphysical Mechanisms of Warm Cloud Precipitation.”Acta Meteorologica Sinica33:97–107 (in Chinese).

Zhou, X., and Z. Gu. 1963. “Several Questions on Cloud/Fog Microphysics and Precipitation.”Science Bulletin06: 1–7 (in Chinese).

Zhu, Z., K. Shi, and M. Huang. 1965. “Cloud and Precipitation Microphysics in the Frontal System (April–May, 1962) on the Hengshan Mountain.” InStudies on Cloud/Fog Precipitation Microphysics in China, edited by Z. Gu, 98. Beijing: Science Press (in Chinese).