面向故障诊断的供水管网水压监测点优化布置方法

李栋 薛惠锋 张文宇

摘要：為解决供水管网故障诊断中准确率不高、经济性不佳的问题，设计了一个基于改进的果蝇优化算法核极限学习机的供水管网故障诊断模型，经验证该模型具有学习速度快、故障识别率高等优点。以该模型为核心提出了基于果蝇优化算法的供水管网水压监测点优化布置方法。该方法首先利用果蝇优化算法形成多组水压监测点方案，然后用供水管网故障诊断模型计算每种方案的诊断准确率，选择其中诊断准确率最高、经济性最好的方案作为候选最优方案，并以此方案为基础，使用果蝇优化算法不断循环迭代，最终找到故障诊断准确率高且经济性最好的水压监测点布置方案。编制Matlab语言代码对提出供水管网水压监测点优化布置方法进行了编码实现，使用实际管网数据进行了实验，发现提出的供水管网水压监测点优化布置方法是一个有效的水压监测点优化布置方法。

关键词：供水；故障诊断；优化布置；核极限学习机；果蝇优化算法

中图分类号：TU991.33 文献标志码：A文章编号：16744764（2018）02005309

收稿日期：20170417

基金项目：国家自然科学基金（U1501253）

作者简介：李栋（1981），副教授，博士生，主要从事智慧水务、智能计算研究，Email： ddli1009@126.com。

Received：20170417

Foundation item：National Natural Science Foundation of China （No. U1501253）

Author brief：Li Dong （1981 ）， associate professor， PhD candidate， main research interests：， Email： ddli1009@126.com.Optimal layout method of water pressure monitoring points for

water supply network based on fault diagnosis

Li Dong1， Xue Huifeng1，2， Zhang Wenyu3

（1. School of Automation， Northwestern Polytechnical University， Xi'an 710072， P. R. China；

2. China Academy of Aerospace Systems Science and Engineering， Beijing 100048， P. R. China；

3. School of Economics and Management， Xian University of Posts and Telecommunications， Xi'an 710061， P. R. China）

Abstract：To improve the accuracy and economy of fault diagnosis， the layout method of water pressure monitoring points is proposed. Firstly， a fault diagnosis model of water supply network is designed by using Modified Fruit Fly Optimization Algorithm （MFFOA） and Kernel Extreme Learning Machine （KELM）. The experimental results show that the fault diagnosis model has the advantages of fast training speed and high accuracy. Then， based on the Fruit Fly Optimization Algorithm （FFOA） and the fault diagnosis model which is proposed in this paper， a water pressure monitoring point layout method is designed. In the method， firstly a set of water pressure detection points is formed by FFOA. Then， the diagnostic accuracy of each scheme is calculated by the fault diagnosis model and the scheme which the diagnosis accuracy is highest and economy is best is chosen to be the candidate optimal program. After that， FFOA algorithm is used to iterate and find the optimal layout of water pressure monitoring solution which has the best accuracy and best economic performance. Finally， the proposed method which is realized is tested by the actual pipe network data. The results show that the method presented in this paper is an effective method to optimize the water pressure monitoring points. Comparing with other methods， the accuracy and economy of fault diagnosis are improved obviously.

Keywords：water supply；fault diagnosis；optimal layout；kernel extreme learning machine；fruit fly optimization algorithm

水压是全面掌握供水管网运行状态及对整个供水系统实施正确调度的重要参数[12]，通过布置水压监测点监测水压实时变化，对供水管网进行优化调度和故障诊断，正在成为复杂供水系统运行管理的必然趋势[35]。理论上水压监测点越多越好，但监测点过多会导致投资过高，因此，如何在监测点有限的前提下，对其位置进行优化布置，使其发挥最大作用是许多学者致力研究的重要问题[6]。

目前，已经提出许多监测点优化布置方法，根据其设计原理的不同可以分为两大类。一类是以聚类分析[2]、信息量最大化[7]等理论为基础的监测点优化布置方法，这些方法所确定的监测点主要用于正常工况下的运行调度，在故障诊断中应用较少，有效性尚未被证实。另外一类方法是以遗传算法、蚁群算法等智能优化方法为手段的监测点优化布置方法。水压监测点布置在本质上属于优化问题[7]。Meier等[8]首次将遗传算法引入到测压点优化布置的问题中，其优选结果明显优于传统的经验方法。随后，Schaetzen等[9]、Kapelan等[10]以及Kang等[1112]、刘书明等[13]对Meier的算法进行了改进，取得了一定的效果。金溪等[14]和许刚等[15]分别将遗传算法和蚁群算法引入监测点优化选址问题中，但并未关注供水管网中的水量变化和渗漏分析。由此可见，目前在水压监测点优化布置研究领域，侧重点主要集中在如何通过聚类、智能优化方法等方法和工具，按照人为设定的筛选原则选择出代表性节点，对于筛选出的监测点是否可以有效诊断管网故障的讨论较少。在设定筛选原则时，较少从经济性角度考虑。

在基于水压监测点优化布置的研究中，主要需要解决如何在供水管网渗漏故障诊断精度满足要求（最高）的条件下投入的水压监测点最少（经济性）。而这个问题可以进一步分解为2个子问题。问题1：如何设计一個高效的供水管网故障诊断模型，使其能够在有限数据下快速精确定位故障位置和故障程度；问题2：如何设计一种高效的监测点选择方法，使其能够在众多节点中选择出数量少、位置佳的监测点。只有在两个问题都兼顾解决的条件下才能有效解决供水管网监测点优化布置的经济性问题。从解决这2个子问题的角度入手，设计了一个面向故障诊断的水压监测点优化布置方法，该方法主要思想是：首先是利用核极限学习机（Kernel Extreme Learning Machine，KELM）建立一个基于改进的果蝇优化算法（Modified Fruit Fly Optimization Algorithm，MFFOA）和核极限学习机的故障诊断模型，接着以该模型为基础，应用面向离散空间的果蝇优化算法（Fruit Fly Optimization Algorithm，FFOA）筛选出满足水压监测点少、故障识别效果优的水压监测点的布置方案，从而实现对供水管网水压监测点的优化布置。

第2期 李栋，等：面向故障诊断的供水管网水压监测点优化布置方法1基于MFFOAKLEM的供水管网故

障诊断模型1.1核极限学习机

传统的机器学习算法，如BP神经网络算法和支持向量机，已经在供水管网故障诊断分析中取得了一定的应用，然而BP神经网络和支持向量机都存在着一些难以克服的缺陷，如：学习速度慢[16]、需要设置参数多等。ELM（Extreme Learning Machine， ELM）[17]作为一种新兴的学习算法，能够克服BP神经网络和SVM的缺点。ELM算法是2006年由Huang等提出的一种新型单隐层前馈神经网络模型，由于其无需反复调整隐层参数，并将传统单隐层前馈神经网络参数训练问题转化为求解线性方程组，利用求得的最小范数最小二乘解作为网络输出权值，整个训练过程一次完成[18]。与其他机器学习算法相比，ELM具有学习速度快、便于实施、不需要太多人为干预、鲁棒性更好等优点[16]。但由于ELM在学习过程中其初始权值随机设定，没有训练优化过程，这会造成算法性能的不稳定，Huang等[19]又提出了基于核函数的极限学习机（KELM），将SVM中核函数的思想运用到ELM中，提高了算法的学习速度，算法的精度以及泛化能力也得到了提升。KELM基本原理参见文献[19]。

1.2果蝇优化算法

果蝇优化算法（FFOA）是由Pan[20]于2011年依据果蝇觅食行为推演出的一种全新的寻求全局最优的新方法。相较于粒子群、鱼群等群体智能优化算法，FFOA具有参数设置少（只有种群大小和最大迭代次数2个参数），运算速度快且易于实现等优点。FFOA的流程为[20]

1）给定群体规模SizePop、最大迭代数Maxgen，随机初始化果蝇群体位置X_axis、Y_axis；

2）果蝇个体利用嗅觉搜寻食物，向随机方向飞行随机距离，RandomValue为搜索距离Xi=X_axis+RandomValue

Yi=Y_axis+RandomValue （1）3）由于无法得知食物位置，因此，先估计与原点之距离Disti，再计算味道浓度判定值Si，此值为距离之倒数Disti=X2i+Y2i（2）

Si=1/Disti（3）4）将味道浓度判定值Si代入味道浓度判定函数（或称为适应度函数Fitness function），用来求出果蝇个体位置的味道浓度Smell。Smelli=Function（Si）（4）5）找出该果蝇群体中味道浓度最佳的果蝇（适用于最小化问题）[bestSmellbestindex]=min（Smelli）（5）6）记录并保留最佳味道浓度值bestSmell与其X、Y坐标，这时候果蝇群体利用视觉向该位置飞去；Smellbest=bestSmell

X_axis=X（bestindex）

Y_axis=Y（bestindex）（6）7）进入迭代寻优，重复执行步骤2）～5），并判断最佳味道浓度是否优于前一迭代最佳味道浓度，并且当前迭代次数小于最大迭代数Maxgen，若是则执行步骤6）。

根据FFOA的原理可知，果蝇在迭代寻优过程中只向当前最优的果蝇个体学习，这种学习方式在进化后期使果蝇之间具有强烈的趋同性，基本丧失了果蝇群体的多样性，该搜索和选择机制容易造成FFOA算法陷入局部极值，从而带来FFOA的早熟收敛问题，制约了FFOA算法的广泛应用。

为了弥补标准FFOA算法存在的易陷入局部极值的缺陷，借鉴人工蜂群速度食物源位置优化策略[21]，通过引入全局引导因子和局部尺度调节因子改进果蝇搜索食物的策略，平衡了FFOA算法局部搜索和全局搜索的性能，使改进的FFOA算法具备动态调节搜索半径的能力，有利于提高算法的搜索精度，加快算法收敛速度。其食物源位置更新改进计算式为Xi=X_axis+Rmin+（Rmax-Rmin）ξiψiRandom（7）式中：ξi为局部尺度调节因子、Ψi为全局调节因子。ξi=1tlocal×1-fi-flocal_bestfglobal_best-flocal_bestβ，

flocal_best≠fglobal_best

rand（-1，1），fi=flocal_best （8）

ψi=（Tmax-ttavg）-extremumTmaxtavgλ（9）式中：Rmin为最小探测距离，Rmax为最大探测距离，参数β、λ为常数，Random是一个随机数，Tmax为最大迭代次数，t为当前全局迭代次数，tlocal为陷入局部极值点之后重新开始搜索的迭代次数，tavg为搜索到一次极值点需要迭代的平均次数，extremum为当前已经搜索到极值点的次数。flocal_best为当前迭代tlocal次中找到的局部最优目标函数值，fi为当前目标函数值，fglobal_best为当前全局最优目标函数值。

在改進的果蝇优化算法（MFFOA）中，全局最优引导因子ψi引导果蝇群对食物源在全局空间的搜索趋势，ψi在迭代初期取值较大，目的是引导果蝇够覆盖全局空间，寻找可能存在全局最优值的区域，提高算法的全局搜索能力；在迭代中期，ψi的值逐渐变小，目的是加强果蝇对局部区域内的搜索精度，避免由于搜索半径过大导致果蝇错过全局最优值，经过这个阶段的探索，全局最优值基本已经确定；在迭代后期，ψi又将逐渐变大，避免迭代后期果蝇群的趋同性导致无法跳出当前搜索区域，无法探索到新的全局最优值。区域尺度调节因子ξi主要用于控制在区域内果蝇搜索的尺度，在区域探索的迭代初期，ξi取值较大，接近1，有利于尽量开拓搜索空间；在区域搜索迭代后期，fi越来越接近flocal_best，ξi愈发接近于0，随之果蝇的搜索半径也越小，局部区域的探索精度也越高。ψi与ξi使MFFOA算法在迭代初期具备较强的全局搜索能力，能够尽可能多地发现全局最优候选解；在迭代中期具备较强的局部搜索能力，提高算法的计算精度和收敛速度；在迭代后期，能够在全局范围内查漏补缺，寻找漏网的最优解，克服传统FFOA算法迭代速度慢，易陷入局部极值的缺陷。

1.3基于MFFOA的KELM供水管网故障诊断模型

选择KELM作为供水管网故障诊断模型的核心算法，但在实验过程中发现，KELM的学习性能和泛化能力受到核参数的影响，这一点在文献[22]中的也有提及。为了提高KELM的分类准确性，有必要对核参数进行优化。为此，尝试应用MFFOA对KELM中的核参数进行调优，建立基于MFFOA和KELM供水管网故障诊断模型，模型处理流程如图1所示。

图1故障诊断流程图

Fig.1Fault diagnosis模型具体实施步骤为：

1）数据预处理。诊断模型的输入数据为供水管网故障发生后各监测点的水压值，为了避免量纲的影响，对各监测点水压数据参照式（10）进行归一化处理。同时将故障位置与故障程度进行统一编码。x′ij=（xij-xminj）/（xmaxj-xminj）（10）2）MFFOA参数初始化。初始化果蝇群体规模SizePop、最大迭代数Maxgen、最大飞翔半径Rmax、最小飞翔半径Rmin等值；设定最佳味道浓度值Smellbest=0，最佳浓度值位置坐标X_axis=（0，0）。

3）果蝇个体随机飞翔。根据式（1），果蝇群中各果蝇在N∧2欧式空间上飞翔随机距离。

4）计算并比较果蝇个体的味道浓度值。根据果蝇的坐标值计算KELM的核参数，应用KELM对训练样本进行故障分类，将KELM分类结果的正确率作为该果蝇的味道浓度值。

5）选取最优果蝇位置。根据式（5）选取果蝇群里中味道浓度值最优的果蝇，并将最优果蝇的味道浓度值GSmellBest以及最优果蝇位置GSemllLocation记入Smellbest与X_axis。

6）果蝇群飞翔。以当前最优果蝇位置X_axis为中心，果蝇个体根据式（7）随机飞翔。并依据步骤4）中方法计算各果蝇的味道浓度值，比较并记录其中最优的果蝇味道浓度值GSmellBest和位置GSemllLocation。

7）更新最优味道浓度值及其位置。比较GSmellBest与Smellbest，若GSmellBest优于Smellbest，则将Smellbest的值更新为GSmellBest，并更新X_axis值为GSemllLocation。

8）迭代判断。若最优味道浓度值大于等于设定的训练目标或迭代次数超过最大允许迭代次数则训练终止，执行下一步，否则更新MFFOA中最小探测距离、最大探测距离等相关参数数据，并跳转到步骤6）继续迭代。

9）根据X_axis值计算得到KELM的最优核参数，并以此建立MFFOAKELM供水管网故障诊断模型。

1.4实例验证

以文献[23]中建立的管网为例，对MFFOAKELM供水管网故障诊断模型的有效性进行验证，供水管网结构如图2所示，图中L为长度，单位为m；D为管径，单位为cm。由于管网规模相对较小，同时出现2个或2个以上管段发生爆管故障的概率较低，因此，仅考虑只有一个管段出现爆管故障的情况，假定图2中标示的7个管段为易爆管段，在易爆管段中间设置虚节点模拟爆点，每个爆点分别设计5种爆管程度，共设计42组试验方案，其中35组实验方案所得数据为训练数据，剩余7组所得数据为测试数据。为了便于分析，对35组用于模型训练的试验方案所得数据进行统一编号，并将此十进制编号作为诊断模型中学习样本的输出数据。表中各测点数据为爆管前后监测点的水压变化值归一化之后的数值，具体数据见原文献。用于测试诊断模型效果的7组实验方案所得数据见原文献，其数据编码模式与训练数据一致。

图2实验管网1

Fig.2No.1 experimental pipe network为了更好地分析MFFOAKELM诊断模型的效果，设计了2个对比模型：1）基于粒子群和支持向量机的PSOSVM供水管网故障诊断模型[23]；2）基于遗传算法和BP神经网络的GABPNN供水管网故障诊断模型。这3个模型均通过Matlab语言编写代码进行了实现。各模型运行中主要参数设置为：1）该模型的迭代次数100、种群规模300、核函数选择poly kernel；2）PSOSVM诊断模型迭代次数100、种群规模300、核函数选择径向基函数RBF[23]；3）GABPNN诊断模型的最大迭代次数100、群体规模100、交叉率为0.7、变异率为0.01。各模型训练与测试结果如表1所示。表1各种模型的计算结果对比

Table 1Comparison for the calculation results of various models模型训练准确率/%测试准确率/%训练时间/sMFFOAKELM10042.860.03PSOSVM10028.574.89GABPNN10042.8615 490.86

由表1可知，各模型训练样本分类准确率均为100%，说明各模型均具备良好的分类性能，但从测试样本的准确率来看，MFFOAKELM模型与GABPNN模型相较于PSOSVM模型对于测试样本的分类正确率更高，说明这两个模型的泛化能力相对更好（注：由于在训练样本量有限，一种故障类型只有一个训练样本，这使得诊断模型对于各故障类型的学习不够充分，也就导致了各模型对于测试样本的分类准确率均不高）。

在水压监测点优化布置方法中要不断从众多节点中选择部分节点作为候选监测点方案，需要使用故障诊断模型来对这些监测点的数据进行学习训练，并依据诊断准确率来判断这些候选监测点是否可以作为正式的候选监测点方案。当管网的节点数量为N时，可选方案数量为Numbers，Numbers的值如式（10）所示。当N值较大时，Numbers将为一个庞大的数值，因此，故障诊断模型的训练时间也是水压监测点优化选择方法中选择何种故障诊断模型需要考虑的一个重要因素。于是对3类模型的学习时间进行了统计，具体结果见表1。由表中各模型的训练时间可知，MFFOAKELM模型训练时间优于PSOSVM模型2个数量级，优于GABPNN模型6个数量级。由此可见，基于MFFOAKELM供水管网故障诊断模型是一个高效的供水管网诊断模型，可以将其作为供水管网水压监测点优化布置方法中的故障诊断子模型使用。Numbers=C1n+C2n+…+Cnn （10）2面向故障诊断的供水管网监测点优

化布置方法2.1面向离散有限空间的果蝇优化算法

传统的FFOA是用于连续空间最优值搜寻，其飞行方式及飞行空间不受限制，而此种飞行方式不适用于有空间限制的离散空间搜索，因此，需要对果蝇优化算法中果蝇的搜索空间、飞行行为以及适应度求解方法做适当修改。

1）搜索空间修改。设果蝇群搜索食物空间为一个N∧N的欧式空间，其中N为待选水压监测点的总数。不失一般性，果蝇i的位置Xi=（xi1，xi2，…，xiM），任意元素xij的取值范圍为{1，…，N}，M为果蝇坐标的维数，可理解为最少监测点的个数，该值在进化过程中会不断优化减少。

2）飞行行为重新定义。设果蝇i的当前位置为Xi=（xi1，xi2，…，xiM），xij∈{1，…，N}，即xij只能在此范围内取值，其中N表示的待选水压监测点的总数，R表示一次飞行的最大距离，即群半径；飞行行为Θ（Xi，M，R）表示果蝇Xi在每一维空间当前位置xij向前飞行r=|R·rand|，rand∈[-1，1]，xij的位置坐标可更新为xij=（xij+r）%N+1，其中“%”表示求余运算[24]。

3）味道浓度值、维度值求解方法。果蝇Xi经飞行行为之后，其坐标数值将发生变化，需要根据其新坐标计算Xi的味道浓度值Smelli与维度值Dimensioni，计算方法为：将果蝇Xi的坐标值按照由小到大的次序进行排序；将序列中的重复值进行合并，经合并之后的果蝇Xi坐标序列值由Mi维减小到M′i维，M′i值即为果蝇Xi的维度值Dimensioni（注：M′i值即为Xi对应监测点的个数）。坐标序列中的那些不重复的值就是供水管网故障诊断监测点布置待选方案，一只果蝇对应一个待选方案；将待选方案选中监测点的监测数据使用MFFOAKELM方法进行训练，将其分类准确率作为果蝇Xi的味道浓度值。

4）优选原则设计。以每一只果蝇的味道浓度值Smell为主要关键字按照由大到小的顺序对果蝇排序，当多个果蝇存在味道浓度值相同时，则以维度值Dimension为次要关键字按照由小到大进行排序。在排序结果中选择分类准确率最优，且维度值最小的那只果蝇作为本轮迭代的最优果蝇。

2.2供水管网监测点优化布置方法设计

已有的面向故障诊断的供水管网监测点优化布置方法主要根据经验选择监测点的位置，再通过监测数据对监测点选择是否合理进行验证，在监测点位置选择时，对于经济性原则考虑不够充分。而笔者提出的面向故障诊断的供水管网监测点优化布置方法则以监测点布置的经济性（监控点最少）和有效性（准确判断故障位置与故障程度）为基本原则，以数据为驱动，以智能优化算法为手段，确定最优的监测点布置方案。供水管网故障诊断监测点优化布置方法具体流程如图3所示，具体步骤为

图3监测点优化布置流程图

Fig.3Optimal layout flow of water pressure monitoring points1）初始化果蝇群体规模SizePop、最大迭代数Maxgen、最大飞翔半径Rmax、最小飞翔半径Rmin，设定最佳味道浓度值Smellbest=0，最佳浓度值位置坐标X_axis=（0，0，…，0M）。

2）果蝇群中各果蝇执行一次“飞行行为”。

3）根据味道浓度值与维度值计算方法求得果蝇Xi的味道浓度值Smelli以及维度值Dimensioni。

4）依据优选原则对果蝇群体进行排序，根据式（9）找出本次迭代果蝇群体中味道浓度最佳的果蝇。

5）将bestSmell与Smellbest进行比较，若bestSmell大于Smellbest，则更新Smellbest=bestSmell，并将X_axis更新为bestSmell的坐标。

6）判断迭代次数gen≤Maxgen是否成立，若不成立，则跳出迭代，执行下一步；若成立，则以X_axis为起点执行步骤2）。

7）返回X_axis，并依据X_axis坐标值计算得到最优水压监测点布置。

2.3算例及分析

为了验证提出的供水管网故障诊断监测点优化布置方法的有效性，以文献[25]提出的管网为例进行分析。管网结构如图4所示，图中L为长度，单位为m；D为管径，单位为m。

图4实验管网2

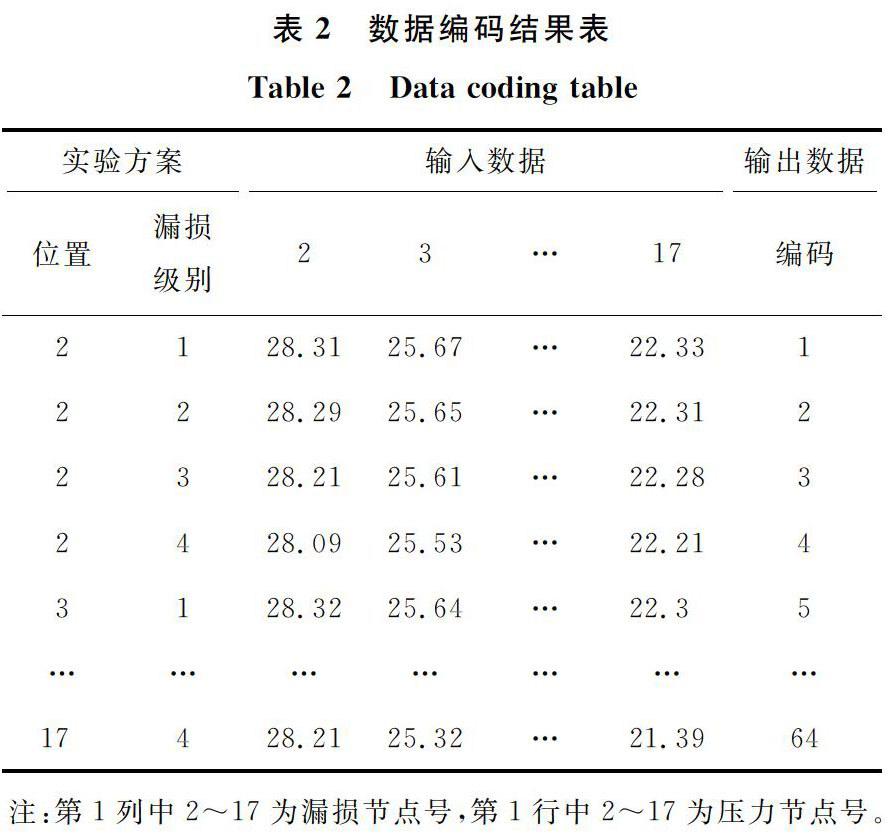
Fig.4No.2 Experimental pipe network当供水管网中各节点出现漏水10%、20%、50%、100%的故障时，各节点压力数据见文献[25]。为了便于分析，参考文献[22]将节点漏水故障进行了分级，将10%漏水故障定为1级，20%漏水故障定为2级，将50%漏水故障定为3级，将100%漏水故障定为4级。为了便于分析，使用前文中提到的故障编号方法，将漏水位置、漏水级别结合起来形成故障编码，将十进制编号作为供水管网故障诊断监测点优化布置方法中计算果蝇味道浓度时学习样本的输出数据。经过重新编码后的数据如表2所示。（注：由于数据量较大，部分数据省略）。表2数据编码结果表

Table 2Data coding table实验方案输入数据输出数据位置漏损

级别23…17编码2128.3125.67…22.3312228.2925.65…22.3122328.2125.61…22.2832428.0925.53…22.2143128.3225.64…22.35…………………17428.2125.32…21.3964注：第1列中2～17为漏损节点号，第1行中2～17为压力节点号。为了更好地比较分析基于FFOA的供水管网故障诊断监测点优化布置方法的效果，构建了2个对比方法：1）基于PSO的供水管网故障诊断监测点优化布置方法，在该方法中故障诊断模型使用的是PSOSVM故障诊断模型；2）另外一个对比模型是基于GA供水管网故障诊断监测点优化布置方法，在该方法中故障诊断模型也是GABPNN故障诊断模型。但在实验过程中发现，基于GA的供水管网故障诊断监测点优化布置方法在长时间运行后水压监测点数仍无法有效收敛，因此，最终将该模型排除在对比模型之外。为了便于比较，优化布置方法与基于PSO供水管网故障诊断监测点优化布置方法的主要运行参数均取同一值，迭代次数均为50，种群规模均为100。两方法以表2数据为样本进行训练与测试，结果如表3所示。

图5果蝇优化算法监测点位置寻优过程

Fig.5FFOA for monitoring points由图中收敛曲线可知，基于FFOA供水管网故障诊断监测点优化布置方法的收敛速度更快，能够在较短时间内寻找到供水管网中适合的监测点布置方案，同时，该方案具有良好的经济性。而基于PSO供水管网故障诊断监测点优化布置模型的收敛速度较慢，其收敛结果也不够理想。表3各种方法寻优结果对比

Table 3Comparison of various methods方法監测点

数量方案监

测点号故障识别

准确率/%本文方法35、13、15

（5、12）100（96.88）基于PSO的供水管网故障

诊断监测点优化布置方法55、9、11、13、15

（5、9、11、13）100（98.44）文献[25]提出

的方法65、7、9、12、15、17

（7、9、12）100|100

（98.44|96.88）注：文献[25]中只给出了7、9、12方案，5、7、9、12、15、17方案是为了满足故障识别率达到100%根据文献[25]的筛选原则得到的水压监测点方案。在文献[25]中只给出了方案监测点号，并未给出故障识别准确率，为了便于比较表中的识别准确率是分别采用MFFOAKLEM模型和PSOSVM模型计算得到，其中“|”之前为MFFOAKLEM计算结果，“|”之后为PSOSVM计算结果。表3进一步将基于FFOA供水管网故障诊断监测点优化布置方法与基于PSO供水管网故障诊断监测点优化布置方法、文献[25]中得出的方案进行了比较。可以看出，基于FFOA供水管网故障诊断监测点优化布置模型（需要3个测压点）要优于后两者（分别需要5和6个监测点），其经济性在准确率要求100%的情况下分别提高了66.7%和100%。而在准确率要求为95%的情况下，其经济性分别提高了100%和50%。除此之外，表3还对同一测压方案采用不同诊断模型的诊断正确率进行了计算比较，发现MFFOAKLEM模型的诊断总体准确率要优于PSOSVM模型，从而进一步验证了MFFOAKLEM故障诊断模型的优越性。总而言之，基于FFOA供水管网故障诊断监测点优化布置方法是一个有效的供水管网故障诊断监测点优化布置方法。

3结论

1）为了提高供水管网故障诊断的效率，采用改进果蝇优化算法和核极限学习机构建了基于MFFOAKELM的供水管网故障监测模型，并在实验管网中对该模型的有效性进行了检验。结果表明，该模型能够将供水管网中的故障进行正确识别，且运行时间较短，是一种高效的供水管网故障诊断模型。

2）以往的供水管网监测点优化布置主要面向供水调度，在面向故障监测方面的研究相对较少，且历史研究成果中对于监测点经济性的考虑不够深入。以此为契机，使用面向离散空间的果蝇优化算法，并结合基于MFFOAKELM的供水管网故障监测模型，设计了供水管网故障诊断的监测点的优化布置方法，通过该方法筛选到的监测点数量少（经济性）且故障识别率佳。

参考文献：

[1] ABRAHAM E， STOIANOV I. Sparse null space algorithms for hydraulic analysis of largescale water supply networks [J]. Journal of Hydraulic Engineering， 2016， 142（3）： 99.

[2] 黄廷林， 丛海兵. 给水管网测压点优化布置的模糊聚类法[J]. 中国给水排水，2001，17（11）：5052.

HUANG T L， CONG H B. The fuzzyed clustering on the optimization arrangemet for pressure monitoring points of water supply network [J]. China Water & Wastewater， 2001， 17（11）： 5052.（in Chinese）

[3] RATHNAYAKA S， SHANNON B， RAJEEV P， et al. Monitoring of pressure transients in water supply networks [J]. Water Resources Management， 2015（2）：115.

[4] PIETRUCHAURBANIK K. Assessment and analysis of proper water supply system functioning [J]. Australian Journal of Earth Sciences， 2014， 38（4）： 409423.

[5] YANG J， XU Z， KONG Y. Chaos identification and prediction of pressure time series in water supply network [C]// Control Conference， IEEE， 2014： 65336538.

[6] 王伟哲，郄志红，刘美侠，等. 基于改进遗传算法的供水管网故障监测点布置优化[J]. 水力发电学报，2012，31（1）：1519.

WANG W Z， QIE Z H， LIU M X， et al. Optimized arrangement of faultmonitor sensors of water supply network by improved genetic algorithm [J]. Journal of Hydroelectric Engineering， 2012， 31（1）： 1519. （in Chinese）

[7] 陳玲俐，庄维坦，何欣. 基于信息最大化准则的供水管网压力监测点布置[J]. 上海大学学报（自然科学版），2015， 21（5）： 640647.

CHEN L L， ZHUANG W T， HE X. Layout of monitoring points in water supply network based on information maximization criterion [J]. Journal of Shanghai University （Natural Science Edition）， 2015， 21（5）： 640647. （in Chinese）

[8] MEIER R W， BARKDOLL B D. Sampling design for network model calibration using genetic algorithms [J]. Journal of Water Resources Planning and Management， 2000， 127（4）： 270279.

[9] DE SCHAETZEN W B F， WALTERS G A， et al. Optimal sampling for model calibration using shortest path genetic and entry algorithm [J]. Urban Water， 2000， 2（2）： 141152.

[10] KAPELAN Z， SAVIC D A， WALTERS G A. Optimal sampling design methodologies for water distribution model calibration [J]. Journal of Hydraulic Engineering，ASCE， 2005， 131（3）： 190200.

[11] KANG D， LANSEY K. Optimal meter placement for water distribution system state estimation [J]. Journal of Water Resources Planning and Management， 2010， 136（3）： 337347.

[12] KANG D， PARSHA M F K， LANSEY K. Approximate methods for uncertainty analysis of water distribution systems [J]. Urban Water， 2009， 6（3）： 233249.

[13] 劉书明，王欢欢，徐鹏，等. 多目标大规模供水管网监测点的优化选址[J]. 清华大学学报（自然科学版）， 2013， 53（1）： 7883.

LIU S M， WANG H H， XU P， et al. Multiobjective genetic algorithms for optimal monitoring station placement in large water distribution systems [J]. Journal of Tsinghua University （Science and Technology）， 2013， 53（1）： 7883.（in Chinese）

[14] 金溪， 曾小平， 高金良，等. 利用遗传算法进行供水管网压力监测点优化布置[J]. 给水排水，2007， 33（Sup）： 346349.

JIN X， ZENG X P， GAO J L， et al. Optimal locating of pressure monitoring station in water distribution system based on genetic algorithm[J]. Water and Wastewater， 2007， 33（Sup）： 346349. （in Chinese）

[15] 许刚， 张土乔， 吕谋. 基于灵敏度分析和蚁群算法的管网监测点优化选择[J]. 中国给水排水， 2007， 23（11）： 94101.

XU G， ZHANG T Q， LV M. Optimized location of monitoring points for water distribution system based on sensitivity analysis and ant colony algorithm [J]. China Water & Wastewater， 2007， 23（11）： 94101.（in Chinese）

[16] 潘红芳， 刘爱伦. 小波核极限学习机及其在醋酸精馏软测量建模中的应用[J]. 华东理工大学学报（自然科学版）， 2014， 40（4）： 474480.

PAN H F， LIU A L. Wavelet kernel extreme learning machine and its application in soft sensor modeling of an industrial acetic acid distillation system [J]. Journal of East China University of Science and Technology （Natural Science Edition）， 2014， 40（4）： 474480. （in Chinese）

[17] HUANG G B， ZHU Q Y， SIEW C K. Extreme learning machine： Theory and applications [J]. Neurocomputing， 2006， 70（1/2/3）： 489501.

[18] 陈绍炜， 柳光峰， 冶帅. 基于核极限学习机的模拟电路故障诊断研究[J]. 西北工业大学学报，2015， 33（2）： 290294.

CHEN S W， LIU G F， YE S. A method of fault diagnosis for analog circuit based on KELM [J]. Journal of Northwestern Polytechnical University， 2015， 33（2）： 290294. （in Chinese）

[19] HUANG G B， ZHOU H M， DING X J， et al. Learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems， Man， and Cybernetics， 2012， 42（2）： 513529.

[20] PAN W C. A new fruit fly optimization algorithm： Taking the financial distress model as an example [J]. KnowledgeBased Systems， 2012， 26（2）： 6974.

[21] 徐龙琴， 李乾川， 刘双印， 等. 基于集合经验模态分解和人工蜂群算法的工厂化养殖pH值预测[J]. 农业工程学报，2016， 32（3）： 202209.

XU L Q， LI Q C， LIU S Y， et al. Prediction of pH value in industrialized aquaculture based on ensemble empirical mode decomposition and improved artificial bee colony algorithm [J]. Transactions of the Chinese Society of Agricultural Engineering， 2016， 32（3）： 202209. （in Chinese）

[22] 李軍，李大超. 基于优化核极限学习机的风电功率时间序列预测[J]. 物理学报，2016， 65（13）： 3948.

LI J， LI D C. Wind power time series prediction using optimized kernel extreme learning machine method [J]. Acta Physica Sinica， 2016， 65（13）： 3948. （in Chinese）

[23] 李楠楠，郄志红，古田均. 供水管网爆管故障诊断的PSOSVM方法[J]. 系统工程理论与实践，2012， 32（9）： 21042110.

LI N N， QIE Z H， FURUTA H. PSOSVM model for pipe bursting diagnosis of water supply network [J]. Systems EngineeringTheory & Practice， 2012， 32（9）： 21042110. （in Chinese）

[24] 李栋， 张文宇. 求解01背包问题的双子群果蝇优化算法[J]. 计算机应用研究，2015， 32（11）： 32733277.

LI D， ZHANG W Y. Double subgroups fruit fly optimization algorithm for solving 01 knapsack problem [J]. Application Research of Computers， 2015， 32（11）： 32733277. （in Chinese）

[25] 梁建文， 肖笛， 张宏伟，等. 供水管网健康监测的压力监测点优化布置[J]. 防灾减灾工程学报，2013， 33（Sup1）： 5157.

LIANG J W， XIAO D， ZHANG H W， et al. Optimal monitoring of pressure in water distribution system for health monitoring [J]. Journal of Disaster Prevention and Mitigation Engineering， 2013， 33（Sup1）： 5157.（in Chinese）