迎风型组合紧致差分的二维地震波场数值模拟

周诚尧,汪 勇,蔡伟祥,桂志先，陈骜卓

(1. 长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100;2. 中石化重庆涪陵页岩气勘探开发有限公司，重庆 408014)

0 前 言

地震正演模拟研究是当前研究地震波传播性质的重要的方法。随着地震正演模拟的发展，人们对于数值结果的精度要求越来越高[1]。常用的数值模拟方法主要有射线追踪法和波动方程法，属于有限差分法。波动方程法然而传统的有限差分数值模拟方法有着两个较为明显的缺点：一是需要用来进行数值模拟的网格点数较多进而增大了计算时间；二是传统的显式差分格式具有较大的数值频散[2]。紧致差分方法是为应对这种情形应运而生的。Lele于1992年提出了对称型紧致差分格式。傅德薰和马延文在紧致差分格式中引入迎风机制[3]，提出了五格点五阶精度的迎风紧致格式[4]。引入迎风机制理论上可以提高紧致差分格式的稳定性。在相同的计算网格中，超紧致差分格式有着更高的精度和分辨率[5-6]，而超紧致差分格式的稳定性相比于普通紧致差分的稳定性有一定幅度的下降。本文所使用的迎风超紧致有限差分数值模拟法是在Chu的三点六阶超紧致差分的基础上引入迎风机制而推导出的三点五阶迎风超紧致差分格式，其稳定性近一步提高[7]。在地震数值模拟应用方面，王书强将紧致差分格式用于弹性波方程的数值模拟[8]，本文所提及方法鲜有文献报道，本文属首次将迎风超紧致差分格式用于二维地震波场数值模拟，而相比于传统的有限差分以及普通紧致差分数值模拟，本文所采用的迎风超紧致有限差分数值模拟方法拥有高精度、高效率以及低频散的优点，相较于原本的三点六阶超紧致差分格式，三点五阶迎风超紧致差分格式具有更高的稳定性。鉴于上述优点，本文将利用迎风型超紧致有限差分格式，对声波方程时间四阶离散格式的位移场空间偏导数进行离散，实现地震波场的数值模拟。

1 迎风超紧致差分格式的原理及应用

迎风超紧致有限差分格式是将迎风机制引入到超紧致有限差分格式中来。Krishnan提出了如下的紧致差分格式[9]：

(1)

其中a1、a0、a2、b0、b1、b2、c1、c2、c0、c3、c4为差分公式系数，h表示网格间距。该公式可以达到六阶精度，相比于一般的紧致差分格式，所用到的网格点数更少。本文中所选取需要引入迎风机制的超紧致格式为三点六阶超紧致差分格式，如下所示：

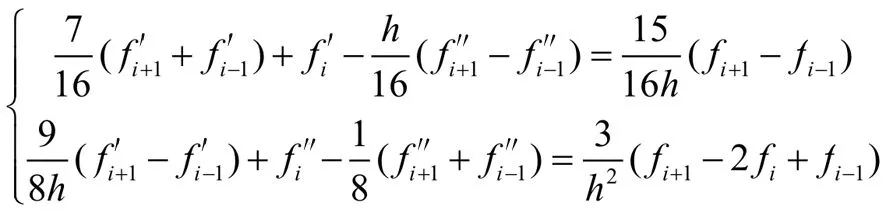
(2)

上述公式引入迎风机制后得到本文所研究的三点五阶迎风超紧致差分格式如下所示：

(3)

接下来则是将上述迎风超紧致差分方法运用于求解声波方程初值问题中来[10]。在各向均匀同性介质中声波方程为如下公式：

(4)

其中的u表示声波在x与z方向上的位移。v则是声波在各向均匀同性介质中的速度。对于上式利用二阶中心差分对时间导数离散可得到如下公式：

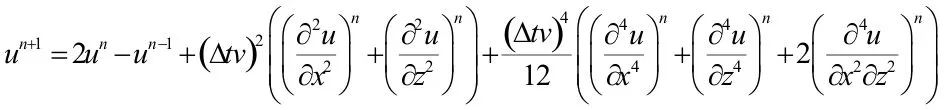
(5)

其中un+1为n+1时刻位移un-1为n-1时刻位移un为n时刻位移。

迎风型组合紧致差分格式的应用关键点在于对其空间导数的计算。本文利用公式(3)求公式(5)中u的z方向上的空间偏导数，矩阵表示为AF=Bu，其中A为公式(3)左端的差分系数矩阵，B为公式(3)右端的差分系数矩阵，u为位移场矩阵。F为位移场空间一阶和二阶导数矩阵。这些矩阵分别如下所示，系数矩阵A：

(6)

F与u分别为：

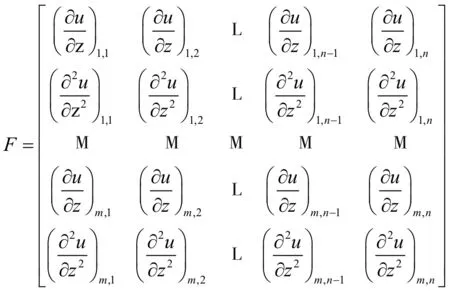
(7)

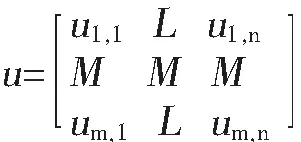
(8)

系数矩阵B如下所示：

(9)

因此对于声波方程的空间导数利用迎风超紧致差分格式逼近后得到如下关系式：AF=Bu，得F=A-1·Bu。若将F定义为声波方程空间z方向上的一二阶导数的集合，那么设FT为x方向上的一二阶导数集合，可知FT=u·(B)T·(A-1)T。而声波方程所需要的为二阶导数部分。因此取z、x方向上的二阶导数部分并命名为F1与FT1，如下所示：

同理对上述结果再次进行矩阵变化可得到z与x方向上的三四阶导数的集合F′及F′T。对x、z依次求导的集合为G，取z、x方向上的四阶导数部分及对x对z依次二阶导数部分，并命名为F′1、F′T1与G1。可知：

(12)

公式(5)变为如下形式：

un+1=2un-un-1+(Δtv)2(FT1+F1)+(Δtv)2(F′1+2G1+F′T1)

(13)

利用关系式(12)及该声波方程所设定初始条件即可进行声波方程的数值模拟。

2 用于声波方程中的频散分析

频散现象是指波的传播相速度与群速度不一致而引起的现象[11-12]。这里我们利用Fourier分析。由于声波方程只需要离散二阶空间导数部分，因此我们只需得知二阶导数的修正波数即可。频散分析大体步骤如下。

1)根据修正波数的定义利用x及z方向上的修正波数kxkz与空间步长h乘积的二次方公式求出差分格式二阶导数x方向上的修正波数和z方向上的修正波数，其中kxh=khcosθ，kzh=khsinθ,θ即波的传播方向与x轴的夹角。

2)再将上述格式代入声波方程中得到如下格式：

2cos(kv′Δt)=2-(vΔt/h)2[(kx″h)2+(kz″h)2]+(vΔt/h)4[(kx″h)4+2(kx″h·kz″h)2+(kz″h)4]/12

(14)

kx″h与kz″h分别为差分格式二阶导数x方向上的修正波数和z方向上的修正波数与空间步长的乘积，v′为数值波速，v为波的真速度。

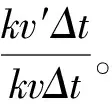
4)做出频散曲线图并与几种常见的紧致差分格式的频散曲线图做对比并分析。

根据频散压制原则，如果不存在数值频散则速度比恒等于1。若偏离1越大，则说明该方法的数值频散越严重。反之，则说明该方法能更好地压制数值频散。图1显示了迎风超紧致格式与其它两种相同精度得差分格式在不同θ时候的速度比曲线，其中α为courant数。

1 USCD; 2 UCD; 3 CD

如上图所示，横坐标φ为波数与空间步长的乘积，纵坐标γ为速度比，其中数值1表示修正波速与理论波速一致。曲线1为迎风超紧致差分方法速度比曲线，曲线2为五阶迎风紧致差分方法速度比曲线，曲线3为五阶一般紧致差分速度比曲线。从图中的速度比曲线可以看出：在不同的角度下，3种方法的的偏移趋势没有明显的变化；从3种曲线的对比看出迎风超紧致方法在偏离1时所对应的横坐标数值，因此根据图中数值可以得到上述4种方法在保证压制频散的时候所需要的最低网格点数为4.0、5.6、6.7个。几种对比方法中，迎风超紧致三点五阶方法对于频散的压制效果最好。

3 用于声波方程中的稳定性分析

对于稳定性分析，本文采用ui,j=ξneIh(kxi+kzj)代入位移场及位移场空间一阶和二阶导数中得到如下表达式：

(15)

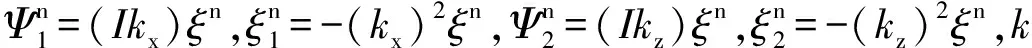
α=vmaxΔt/h<0.81

这里和未引入迎风机制的三点六阶超紧致差分格式的稳定性进行一个对比，如表1所示。

表1 不同方法courant数对比

迎风超紧致格式具有较高的courant数，即稳定性高，普通紧致六阶差分方法的courant数(即稳定性)明显高于三点六阶超紧致差分格式，而与未引入迎风机制的三点六阶超紧致格式相比，三点五阶迎风超紧致格式的稳定性有着明显的提高。

4 截断误差分析

对于精度的分析本文采用截断误差的对比分析。表2为由Taylor截断误差分析所得，内容为几种方法的二阶导数的截断误差。可以得到以下结论：迎风超紧致格式不仅具有超出中心差分格式的精度，和标准紧致差分格式相比，在同样利用三点的情况下具有更高的精度。

表2 二阶导数不同方法截断误差

5 模型试算

5.1 均匀介质模型

图2波场快照所选取均匀介质模型的声波速度设定为4 000 m/s，空间步长均取为25 m，激发位置位于模型的中心处，震源为20 Hz雷克子波。图中x轴表示为模型的横向长度，y轴为纵向长度。小节将三点五阶迎风超紧致格式与另外3种方法对均匀介质进行数值模拟后的结果进行对比，图2的时间步长Δt=0.001 s，空间步长则尽量取较大的数值以对比4种方法哪种在频散压制方面具有优势。图2的均匀介质模型的长度及深度均取4.8 km这个较大数值。

图2 空间步长为25 m,400 ms时各方法波场快照

从图2可知普通紧致差分所模拟得到的结果存在频散现象。当空间步长取到25 m时，七点六阶差分格式与普通六阶紧致差分格式均有强烈的频散现象，三点六阶超紧致差分格式有轻微的频散现象。而三点五阶迎风超紧致差分格式的结果几乎没有频散现象；将上述几种方法分别对应比较可知，三点五阶迎风超紧致差分格式优势相当明显。

5.2 水平介质模型

水平介质模型设置为两层，每层的厚度为2 km，长度设置与深度相同取4 km。其中水平介质模型速度设置为：第1层波速为4 000 m/s；第2层波速设为4 500 m/s。以地表中心进行激发，震源为20 Hz雷克子波，时间与空间步长分别取0.001 s与10 m。将迎风超紧致差分格式方法应用于该模型中进行数值模拟。结果如图3所示，图中x轴为模型横向长度，y轴为声波传播时间。

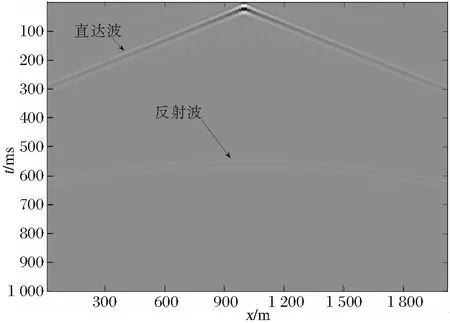
图4 水平层状介质模型声波方程数值模拟地面地震记录

图3中波场快照清晰得表现出声波在水平层状介质中传播效果，没有数值频散和不稳定数值结果，图3中所得到的地面地震记录反映清晰，直达波、反射波显示清楚，说明该方法能够有效而清晰地模拟声波在多层各向同性介质模型中的传播。

6 结 论

从地震正演模拟的声波方程数值模拟入手，简单介绍了传统的有限差分，由于精度的要求问题，往往不能满足需求，因此引出了三点五阶迎风超紧致差分方法，也是本文主要介绍的内容，它具有精度高、分辨率高、高稳定性、网格节点数需求较少等优点。在介绍了三点五阶超紧致差分格式的原理后，对比分析了该差分格式的截断误差、稳定性和频散等问题，随后做了均匀介质的声波方程数值模拟，并与其它方法进行对比分析，得出的结果是该方法不仅在精度上有着较为明显的优势，而且对频散的压制方面也有很好的效果。最后，将这种超紧致差分格式应用于对层状介质的声波方程数值模拟中，取得了良好的效果，表明该方法能够有效地模拟声波在多层各向同性介质模型中的传播。相比原来的三点六阶超紧致差分格式，三点五阶迎风超紧致差分格式的稳定性有明显的提高。

本文在进行声波方程数值模拟时，由于该方法使用的是均匀网格，而且对于地震正演模拟来说，只是对均匀介质及水平层状介质的模拟还是不够的，迎风超紧致格式的优点没有完全得体现出来。今后的研究中，可以应用于其他非均匀的网格中，比如交错网格，亦可以结合其他复杂介质进行地震正演模拟分析。

参考文献：

[1] Komatissch D, Barnes C, Tromp J. Simulation of anisotropic wave propagation based upon a spectral element method[J]. Geophysics, 2000, 65(4): 1251-1260.

[2] Fu D X, Ma Y W, Liu H. Proceedings, 5th International symposium on CFD. Sendai. 1993 1:104.

[3] Fu D X, Ma Y W. A high order accuracy difference scheme for complex flow fields[J]. J ComputPhys,1997(134): 1-15.

[4] 王芳芳. 紧致差分格式的理论与分析[D]. 辽宁：东北大学理学院，2010.

[5] Lele S K. Compact finite difference scheme with spectral-like resolution[J]. Journal of Computational Physics, 1992,103(1):16-42.

[6] 林东, 詹杰民. 浅水方程组合型紧致差分格式[J]. 计算力学学报, 2008, 25(6):791-796.

[7] 王书强，杨顶辉，杨宽德. 弹性波方程的紧致差分方法[J]. 清华大学学报(自然科学版)，2002，4(8)：1128-1131.

[8] 梁贤，田振夫. 求解Navier-Stokes 方程组的组合紧致迎风格式[J]. 计算物理，2008,25(6)：660-665.

[9] Krishnan Mahesh. A family of high order finite difference schemes with good spectral resolution[J]. Journal of Computational Physics, 1998(145): 332-358.

[10] Ehaterinaris J A. Implicit, high-resolution, compact schemes for gas dynamics and aeroacoustics[J]. Journal of Computational Physics, 1999,156(2):272-299.

[11] Blayo E. Compact finite difference schemes for ocean models[J]. Journal of Computational Physics, 2000,164(2):241-257.

[12] Sengupta T K, Ganeriwal G, De S. Analysis of central and upwind compact schemes[J]. Journal of Computational Physics,2003,192(2):677-694.