BF模式匹配算法的改进
,
(1.嘉应学院 计算机学院,广东 梅州 514015; 2.广东暨通信息发展有限公司,广东 广州 510000)
0 引言
随着计算机网络时代的飞速发展,人们足不出户就可以做任何事情,比如网购、看新闻、发表网络小说等。网络的利民之处众所周知,但也时不时看到这样的新闻,网银密码给黑客窃取,某公司网站被黑客“逛”,顺手拿走内部资料……因此,网络的安全性关系到人们的切身利益。在网络安全领域中,具有网络安全性的入侵检测系统也越来越广泛地被应用到生活中,设计者也越来越关注入侵检测系统的关键技术——模式匹配算法。在前人不断的研究和积累中,对模式匹配算法及其改进已有丰富的成果,如典型的单模式算法有Brute-Force(BF)算法[1-3]、Horspool算法[4]、KR算法[5],文献[6-7]提到的多模式算法主要有Aho-Corasick(AC)算法、ACBM算法及文献[8]提到的Wu_Mander(WM)算法。为了提高算法的性能,研究者在这些算法的基础上对其进行不断地改进。本文从模式串的首字符与模式串的相关特点着手,对BF算法进行改进,称改进后的BF算法为Improved_BF算法,后文简称I_BF算法。
1 BF算法
模式匹配的定义是:对于给定的文本串T=T0T1……Tn-1(n为文本串的长度)和模式串P=P0P1……Pm-1(m为模式串的长度),(n远大于m)(T和P都建立在有限字符集上,大小为σ),要求在主串T中寻找等于模式串P的子串,如果在T中存在等于P的子串,则称匹配成功,函数值返回为P中第一个字符相等的字符在主串T中的序号,否则称为匹配失败,函数值返回为0,此过程就是模式匹配。在许多改进的算法中,当匹配成功时,函数值返回P中所有匹配的字符在T中的位置。
经典的单模式匹配算法BF(Brute-Force)算法是朴素模式匹配算法[9]。BF算法的思想就是将目标串T的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较T的第二个字符和 P的第二个字符;若不相等,则比较T的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。
BF算法易于理解,但由于要比较的字符多,模式匹配的时间代价主要用于比较字符,所以时间效率不高。
BF算法最好情况是,第一次匹配即成功,模式串刚好与目标串的开头长度为m的字符串T0T1……Tm-1匹配,此时比较次数为模式串长度m,时间复杂度为O(m)。最坏情况下要进行m*(n-m+1)次比较,时间复杂度为O(m*n)[10]。
2 改进的BF算法——I_BF算法
2.1 已有改进算法
由于BF算法从T中的第一个字符开始进行比较,没有考虑已取得的部分匹配的情况,为了减少比较次数,提高匹配效率,文献[1]对BF算法进行了改进,新改进的算法称为EBF算法。EBF算法中抽象模式串中的字符是从整个模式串中选出来的特殊的字符, 它的内容体现了整个模式串的内容特征,其字符的位置贯穿整个模式串,相对于BF算法从头开始一一进行匹配,能加快字符匹配失败的速度,其匹配效率可能就是BF算法一一匹配时的几倍或更高。
虽然文献[1]中的EBF算法优于BF算法,但能否根据模式串本身的特点在文本串的位置,从其它角度对BF算法进行改进呢?
2.2 I_BF算法描述
为方便描述改进的BF算法,在此对一些变量说明如下:
字符指针变量text:存放文本串
字符指针变量pattern;存放模式串
整型变量Tlen:文本串长度
整型变量Plen:模式串长度
整型变量sumimp_BF:用于统计I_BF算法所匹配的总字符数
整型变量tangimp_BF:用于统计I_BF算法所匹配的趟数,初值为1
字符型变量firstchar:Pattern中的首字符,初值为Pattern[0]
I_BF算法的思想是:扫描整个文本串text,查找文本串中与模式串pattern的首字符相同位置进行匹配,匹配方式是左匹配,不相同的位置不进行匹配,直到扫描完成。
2.3 I_BF算法的匹配阶段
在匹配阶段,需要定义如下几个局部变量:
整型变量k:用来记录目标串text的下标值,初值为0,终值为Tlen-1。
整型变量i:用来记录文本串中出现firstchar的位置,如果与模式串pattern的j位置字符匹配,则自增。
整型变量j:用来记录文本串pattern的下标值,初值为0,如果与字符串text的i位置字符匹配,则自增。
I_BF算法的匹配过程是通过判断文本串text的当前下标的值是否与模式串pattern的首字符相同,若相同则进行匹配,若不相同则不进行匹配。算法的匹配过程描述为:
1)初始化相关变量:k=0;
2)当k 3)若text[k]等于firstchar,则执行4),否则执行8); 4)进行变量i的赋值,即i=k; 5)进行变量j的赋值,即j=0; 6)当i,j均小于text、pattern的长度时,执行6); 7) text的子串textˊ开始与pattern进行左匹配,若匹配成功,变量i、j均自增,执行6);若不匹配,跳出匹配窗口执行8); 8)k++,回到2); 9)匹配结束。 算法的程序段为: k=0; while (k { if (text[k] == firstchar) { inti=k; intj= 0; while(i< Tlen &&j< Plen) { if (text[i] == pattern[j]){ i++; j++; } else break; } } k++; } 为了测试I_BF算法,在程序段中添加两个语句,一个是统计I_BF算法所匹配的总字符数变量sumimp_BF自增功能语句,另一个是用于统计I_BF算法所匹配的趟数tangimp_BF自增功能语句。修改后的程序段为: k=0; while (k< TLen) { if (text[k] == firstchar) { tangimp_BF++; inti=k; intj= 0; while(i< Tlen &&j< Plen) { sumimp_BF++; if (text[i] == pattern[j]) { i++; j++; } else break; } } k++; } 为了说明I_BF算法性能的优越性,在此通过几个简单实例从字符比较次数及比较趟数两方面对BF算法及I_BF算法进行比较。 取模式串P为“taobao”,长度为6。 表1是对两种算法在比较字符个数方面的实验结果。 表1 BF算法与I_BF算法比较字符个数 表2是对两种算法在比较字符趟数方面的实验结果。 表2 BF算法与I_BF算法比较趟数 表1、表2中,实例1至4都是匹配成功的实例,当文本串中出现模式串首字符的次数不等于文本串长度时,I_BF算法总是优于BF算法;实例5和6是匹配失败的实例,其中实例5是文本串中不出现模式串首字符,此时I_BF算法只需要进行预处理,所花时间也是预处理阶段,而不需要进行匹配,所以此种情况是最优,而实例6是文本串中的字符全部都是模式串首字符,此时I_BF算法与BF算法相当。 在实际应用中,文本串中的字符都是模式串首字符的情况很少,所以,在实际应用中,I_BF算法的应用性还是较大的。 I_BF算法在匹配阶段的跳跃次数完全取决于firstchar在T中出现的次数,算法最好情况是T中没有出现firstchar,此时时间复杂度是O(1);最坏情况T中所有字符都是firstchar,即出现n次,则此阶段的时间复杂度是O(n*m)。 综上分析,I_BF算法性能比BF算法优。 为了检测I_BF算法的性能,从不同角度对BF算法、I_BF算法进行测试。测试的操作系统用Win 7,实现算法的软件是Visual Studio 2010。 测试文本选用两方面文本进行: 测试一: 文本是随机输入连续的字符串,字符长度为256960,测试的模式串分两种情况从匹配字符个数、匹配次数、所花时间三方面进行比较,分别是: 第一种情况是模式串在文本串中,也就是匹配成功情况,运行结果如图1所示。 图1 随机字符串匹配成功 图1中,右边栏的结果是匹配结果,每两行为一组,每个测试时间为运行10万次所取的平均时间。(1)第一组测试结果是模式串为"abc",长度为3;(2)第二组测试结果是模式串为"abcde",长度为5;(3)第三组测试结果是模式串为"abcdefabcde",长度为11。从运行结果可知,I_BF算法的比较趟数、比较字符个数和匹配时间都比BF算法少。 第二种情况是模式串不在文本串中,也就匹配失败情况,如图2所示。 图2 随机字符串匹配失败 三组测试模式串分别是:"zyz"," xyzwx "" xyzwxvwxsyuu ",长度分别是:3,5,12。由于模式串不在文本串中,所以I_BF算法不需要进行比较字符串,所花的时间是在查找首字符,结果比匹配成功时相对于BF算法所花时间更少。 测试二: 文本是一篇英文小说,字符长度为480865,测试的模式串是单词,分两种情况,一种是模式串在文本串中,也就是匹配成功情况。为了更直观地说明I_BF算法的优越性,现用表格形式进行两种算法在比较趟数、比较字符个数、运行时间三方面展示,分别如表3、表4、表5所示;另一种是模式串不在文本串中,也就匹配失败情况,两种算法在三方面的对比综合如表6所示。 表3 匹配成功时BF算法与I_BF算法比较趟数结果对比 表4 匹配成功时BF算法与I_BF算法比较字符个数结果对比 表5 匹配成功时BF算法与I_BF算法运行时间结果对比 从表3、4、5可以看出:I_BF算法在比较趟数、比较字符个数、运行时间,均比BF算法有很明显的优势,特别是运行时间方面,约为BF算法的43.2%。在I_BF算法中,模式串在文本串中出现的次数越少,所比较趟数和运行时间越少。 表6 匹配失败时BF算法与I_BF算法情况对比 从表6可以看出,当匹配失败情况下,无论模式串长度如何,I_BF算法所花时间远远少于BF算法,约为25.17%,而且实验发现,模式串长度越大,I_BF算法运行时间越少。 从以上实验可证明,I_BF算法是一个性能很好的改进算法,这是因为I_BF算法在匹配时只需要考虑P中首字符在T中出现的位置,这样大大增大了跳跃距离,减少了匹配次数。因此,I_BF算法效率更高。 典型BF算法从T中的第一个字符开始进行比较,每次匹配都是把P的首字符与当前匹配窗口的T的下一个字符开始匹配,完全没有利用已取得的部分匹配字符,导致效率低。本文提出的I_BF算法的移动距离是根据P中首字符在T中的位置来确定,匹配方式与BF算法一样从左到右。从实验结果和综合分析可知,由于I_BF算法能够很大幅度地跳过坏字符,大大减少了移动的次数和比较的字符个数,减少了匹配时间,而且I_BF算法在编程方面容易实现,所以I_BF算法在实际应用中更实用、更有效。 参考文献: [1] 蔡 恒,张 帅.基于BF算法改进的字符串模式匹配算法[J]. 电脑编程技巧与维护,2014(22):14-15,33. [2] 王文霞. BF模式匹配算法的探讨与改进[J]. 运城学院学报,2016,34(6):63-65. [3] 朱宁洪.字符串匹配算法Sunday的改进[J]. 西安科技大学学报,2016,36(1):111-115. [4] 曹海锋,张维琪.对 Horspool 算法的改进[J]. 企业技术开发,2015,34(6):46-47,69. [5] 杨 品,吴宇佳,刘嘉勇.基于KR-BM算法的多模式匹配算法改进[J]. 信息安全与通信保密,2014(11):117-120. [6] 许家铭, 李晓东,金 键,等. 一种高效的多模式字符串匹配算法 [J].计算机工程,2014,40(3):315-320. [7] 胡桂淼. 多模匹配算法及在入侵检测系统中的应用[D].杭州:浙江工业大学,2014. [8] 巫喜红.入侵检测系统中Wu_Manber多模式匹配算法的研究[J].计算机应用与软件,2008,25(8):114-125. [9] 陈洪涛. 入侵检测中多模式匹配算法的应用研究[D]. 天津:天津理工大学,2015. [10] 李春葆. 数据结构教程[M]. 北京:清华大学出版社,2013.2.4 两种算法的实例比较

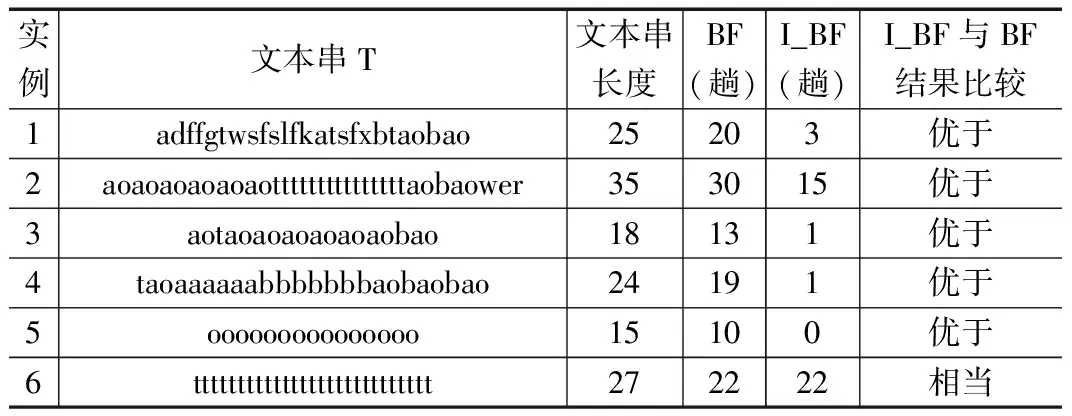
2.5 I_BF算法性能分析
3 I_BF算法性能测试
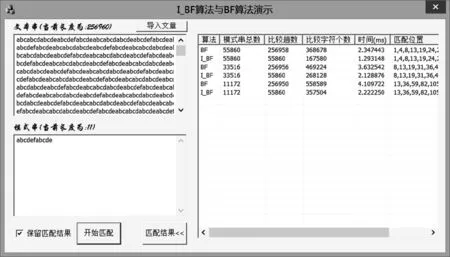
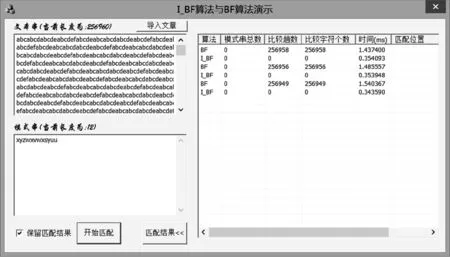

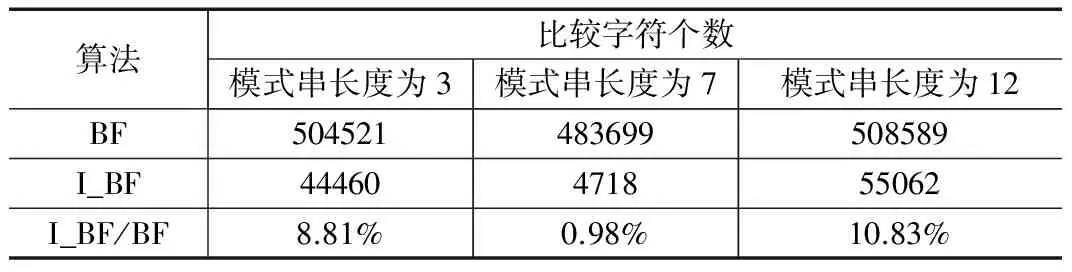


4 结论

