基于RNN的试题相似度计算模型研究与实现

梁圣*



基于RNN的试题相似度计算模型研究与实现

梁圣*

（湖南工业大学计算机学院，湖南株洲，412007）

由于对试题库的管理缺乏相应的相似度检测手段，导致试题库会存在相似试题和重复试题。这些高相似度试题不仅会严重影响了试题库的管理,而且对知识的考核与评估、考试系统测评等都造成不良影响，因此需要采取必要的技术针对知识库中的相似试题进行处理。为此本文进行了试题库相似度计算的相关研究，展开了基于循环神经网络(RNN)的相似度计算模型的相关研究。

试题，循环神经网络，长短时记忆网络，TF-IDF，相似度

引言

随着信息技术的快速发展，各级学校都在大力发展信息化教育，纷纷建立起大规模试题库，以便进行网络化测评。但由于目前题库在进行试题录入时缺乏一定的检测手段，导致试题库会存在相似试题和重复试题，重复试题指的是完全一样的试题，相似试题指的是不完全一样，但是考察的知识点和出题方式或者答案是一样的试题。试题库中存在高相似度的试题，甚至重复的试题不仅会严重影响了海量试题的管理,而且对知识的考核与评估、考试系统测评等都造成不良影响，需要采取必要的技术对试题库中的相似试题进行处理。

1 相关研究工作

Wang针对海量题库中存在雷同试题的问题, 提出一种识别雷同试题的方法及试题去重模型，用于实现试题相似度的计算[1]。Zhi应用文本分类的主流处理技术，开发出一个基于向量空间模型的试题分类系统[2]。Tang 基于多示例学习方法，结合文本的元数据特征对试题重复的检测方法进行了改进，提出试题相似度计算方法[3]。Dong利用词嵌入技术对试题库数据进行处理，通过计算文本空间向量间的余弦值得出题干与知识点的语义相似度[4]。Chen提出的特征抽取算法, 解决了传统的从单一或片面的测试指标进行特征抽取所造成的特征过拟合问题[5]。Yang通过构建关系树提高了信息过滤的精确度[6]。

2 基于RNN的试题库相似度计算模型

2.1 相似度计算模型结构

为了进行试题库中试题间的相似度计算，需要首先给出句子编码模型，本文结合RNN在文本分类任务中的良好表现，提出了基于BI-LSTM试题编码模型，具体网络结构如下：

针对两个需要匹配的试题对，首先分别进行分词、归一化以及其它的预处理操作，然后采用词向量进行词的向量化表示，这样每个试题都被表示成了L*D二维向量，L表示句子对应的最大词序列长度，D为词向量的维度。由于采用深度网络进行编码时需要保持输入长度的一致性，因此，需要根据语料库试题的平均长度提前设定好L的取值。如果试题的词序列长度大于L，则进行截断，即仅保留前L个词；如果试题的词序列长度不足L，则需采用特殊字符进行补位，补足至L个词。将句子转化为二维向量以后，便输入到深度网络进行编码，以获取试题的向量表示。为了保持用于编码的深度网络训练充分通常，句子A和句子B采用的编码网络的权值是共享的。得到试题的向量化表示以后，通过相似度计算便可以得到两个试题间的相似度。

基于上述试题编码模型，可以得到整个试题相似度计算模型如下图所示。

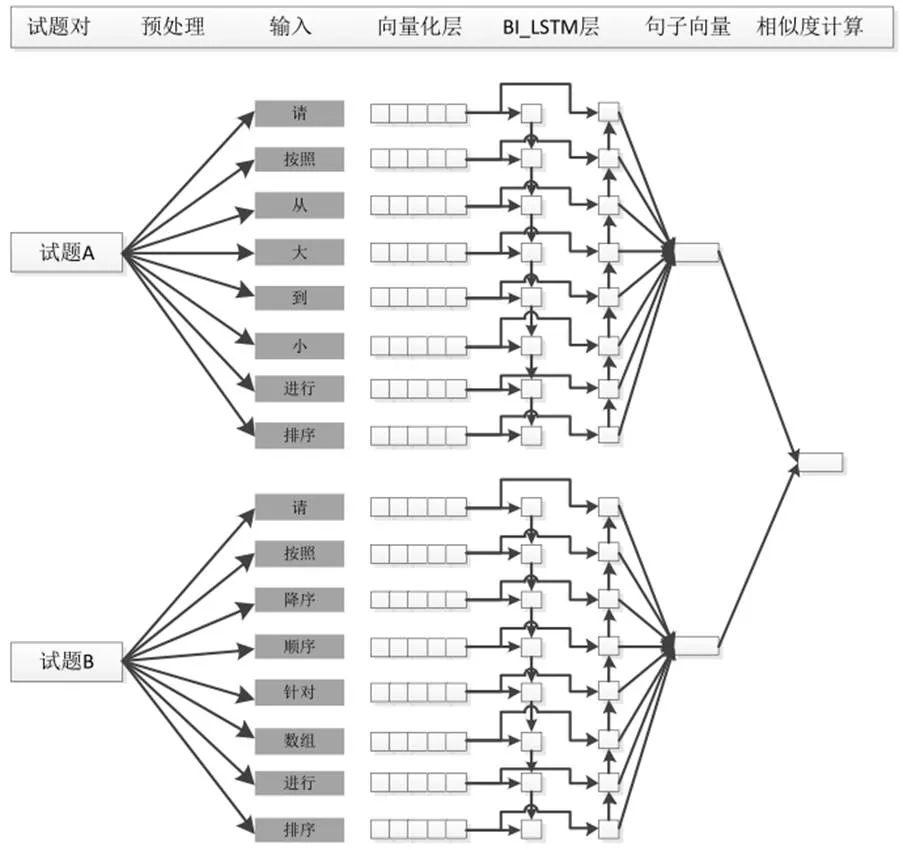
图2 试题相似度计算模型

通过上图可以看出，该模型采用了2层LSTM神经网络进行试题内容编码，首先采用两个LSTM对试题内容进行正反向编码。第一层采用正向LSTM对试题内容进行编码，LSTM的隐含单元个数为N，第二层采用反向LSTM进行试题内容编码，LSTM的隐含单元个数同样为N，然后将正反向LSTM的编码按照时间维度进行拼接，得到一个L*2N的二维向量，这里的256是正反向编码按照时间维度累加的结果。用Bi-LSTM完成试题内容的编码后，需要采用Max-Pooling进行池化，将Bi-LSTM编码结果降维到1维，即1*2N。试题A和试题B经过Bi-LSTM网络编码以及Max池化以后，均转变成了1*2N维度的向量，便可用相似度函数来衡量二者的相似度，LSTM权重均采用he_uniform方式进行初始化，激活函数为RELU。

2.2 相似度计算处理过程

相似度计算模型采用余弦相似度作为相似度的度量。亦可采用其它相似度度量方法，如点乘，或将两个试题表示向量进行拼接，输入到新的神经网络进再进行相似度度量。

试题库相似度模型以试题对作为输入，即一对待计算相似度的试题。与基于词向量的相似度计算模型不同，该模型无需对进行试题内词汇TF-IDF的计算，也不必去除高频词以及停用词，因为LSTM在处理时序输入时由于各个控制门的存在，能够自动的给不同时刻的输入赋予不同的权重，如果编码的当前输入对整个输入序列无关轻重，那么LSTM在编码当前输入时对整个LSTM上下文影响也就降低了，进而当前时刻的隐含状态信息也不会有大的变化，这样当前时刻输入对LSTM后续状态的影响也将降低。

试题对中的试题A和试题B通过查询词向量文件得到其相应的词向量，这样试题A和试题B变成L*D的二维矩阵，其中L指的是输入试题的长度，D是指词向量维度。随后开始利用LSTM网络对这个二维矩阵进行正反向编码，分别得到两个L*2N的二维矩阵，L同样指的是输入试题的长度，N是指循环神经网络的隐含节点个数。之所以得到L*2N的二维矩阵是由于正反向编码结果均是L*N，二者按照时间维度进行拼接后，变得到了L*2N的二维矩阵。通过池化操作，将二维矩阵降维到一维，进而通过相似度计算模块进行试题A和试题B相似度的计算。

在试题相似度模型中采用了Max池化操作，能够最大程度的保留试题特征，这也是在判断试题相似度时主要考虑的因素。在后面实验中，将进一步对比不同的池化操作对最终相似度判断结果的影响。

3 实验及结果分析

3.1 实验环境

本文在进行试题库相似度研究时，实验环境配置如下表1所示。

表1 实验环境配置

3.2 实验数据准备

实验数据是从互联网抓取的计算机相关题目，共标注出7124对相似试题，为了降低标注的工作量，在进行标注时仅通过0/1标注，表示当前试题对是否为相似试题，具体示例如下：

表2 标注示例

相似度结果为1表示试题1和试题2为重复试题；相似度结果为0则表示二者相似程度较低，不构成重复试题。对全部标注数据进行了8:2划分，80%的数据作为训练，20%的数据作为测试，具体语料划分情况如下：

表3 数据划分

训练数据和测试数据分布相同。

考虑到当前的试题库规模较小，在进行Bi-LSTM试题相似度计算模型时，同样使用了预先训练的词向量进行试题库相似度计算模型训练时的词汇分布式表示。词向量训练语料与训练过程中滑窗大小直接影响训练结果，超出窗口的词语与当前词语之间的关系不能正确的反映在模型之中，但如果单纯的扩大窗口大小会增大训练的复杂性也会大大增加训练时间。本课题在训练词向量时将上下文窗口设置为7，迭代轮次为10，采用了CBOW方式进行词向量训练。分别训练了不同维度的词向量，进行对比试验，比较不同维度词向量对相似度计算结果的影响。

在本文中，训练词向量模型数据总量10W篇计算机相关文章以及部分计算机试题。在训练完成后，观察与“排序”，“数组”以及“矩阵”三个词汇最为相似的Top15词汇，具体如下表所示。

表4 Word2vec词相似度

3.3 实验结果分析

（1）不同词向量维度下的实验结果分析

基于分布式表示的词向量可以表现文本的语义信息，词向量维度影响文本语义信息的表现能力，从而影响试题相似度计算结果。训练语料越多，词向量的维度应该相应提高，同时词向量在后续任务中可以表现出更好的性能。本文分别训练不同维度的词向量，然后进行对比实验，实验结果如下表5所示。实验的LSTM隐含层个数均设置为128，采用Early-Stop避免训练的过拟合。模型输入的最大句子长度为128，长度大于128的部分将被丢弃，不足128句子将通过追加“OOV”补足到128，OOV表示out of vocab的词汇。词向量采用了预训练的Word2vec，并伴随着模型更新。模型采用Adam方式进行优化，初始学习率为2e-4，batch大小设置为64。

针对试题相似度计算模型的评价，采用分类模型中通用的评价，即查准率、召回率以及F1值。查准率计算公式如公式（1）所示。其中，Sr表示判断为相似且真实相似的试题对个数，Sa表示模型认为相似的试题对个数。

召回率是正确分类的文本数与应有的文本数的比值，计算公式如公式（2）所示。其中，Sr表示判断为相似且真实相似的试题对个数，So表示真实相似的试题对个数。

F1值是准确率和召回率的综合衡量，如下：

不同词向量维度下的具体实验结果如下表所示。

表5 选取不同维度词向量的训练结果

随着词向量维度的增加，达到模型最优迭代所需的轮次越来越少，这是因为词向量维度的增加导致了整个试题相似度计算模型的参数大幅度增加，从而使得模型整体上达到最优，所需进行的参数调整容易进行。

随着词向量维度的增加，模型在测试集上的准确率是先增后降的，具体如下图所示。词向量维度的增加导致模型整体参数规模增加，而训练数据较少，从而使得模型训练过程出现了过拟合，使得模型准确率下降。

图3 不同维度词向量的准确率

（2）不同隐含层个数下的实验结果分析

在采用LSTM神经网络进行模型训练时，隐含层神经单元个数将直接影响整体模型的最终性能，为此本文进行了不同隐含层个数下的BI-LSTM对比实验，具体实验结果如表6所示。

表6 选取不同隐含层神经单元个数的训练结果

随着隐含层神经单元个数的增加，达到模型最优迭代所需的轮次越来越少，这是因为隐含层神经单元个数的增加导致了整个试题相似度计算模型的参数大幅度增加，使得模型整体上达到最优，使得参数调整容易进行。

随着隐含层神经单元个数的增加，模型在测试集上的准确率是先增后降的，具体图4所示。结果表明隐含层神经单元个数的增加导致模型整体参数规模增加，而训练数据较少，使得模型训练过程出现了过拟合，使得模型准确率下降。

图4 不同神经单元个数的精确率

4 结束语

本文进行了试题库相似度计算的相关研究，展开了基于循环神经网络的相似度计算模型的相关研究，并对比了不同词向量维度以及LSTM隐含层神经单元个数对相似度计算结果的影响。实验结果表明，该模型能够完成试题相似度评价任务。

[1] 王宇颖, 陈振, 苏小红. 自动组卷中试题去重技术研究[J]. 哈尔滨工业大学学报, 2009, 41(01): 85-88.

[2] 植兆衍, 彭宏. 基于向量空间模型的试题分类系统[J]. 计算机工程与设计, 2008, 29(12): 3227-3229, 3233.

[3] 汤世平, 樊孝忠. 基于多示例学习的题库重复性检测研究[J]. 北京理工大学学报, 2005, 25(12): 1071-1074.

[4] 董奥根, 刘茂福, 黄革新, 等. 基于向量空间模型的知识点与试题自动关联方法[J]. 计算机与现代化, 2015, (10): 6-9.

[5] 陈治纲, 何丕廉, 孙越恒, 等. 基于向量空间模型的文本分类系统的研究与实现[J]. 中文信息学报, 2005, 19(1): 36-41.

[6] 杨玉珍, 刘培玉, 姜沛佩, 等. 向量空间模型中结合句法的文本表示研究[J]. 计算机工程, 2011, 37(3): 58-60.

Research and Implementation of Test-Items Similarity Computing Model Based on RNN

LIANG Sheng*

(School of Computer Science, Hunan University of Technology, Hunan Zhuzhou, 412007, China)

Due to the lack of corresponding measures of similarity in the management of the test-item database, there will be similar test items and duplicate test items in the test-item database. These high similarity questions will not only seriously affect the management of the test-item database, but also have an adverse effect on the assessment and assessment of knowledge, test system evaluation, etc. Therefore, it is necessary to adopt the necessary techniques to deal with similar questions in the knowledge base. In this chapter, the related researches on the similarity calculation of the test bank were carried out, and the related research on the similarity calculation model based on the recurrent neural network (RNN) was developed.

Test-Items; RNN; LSTM; TF-IDF; Similarity

10.19551/j.cnki.issn1672-9129.2018.01.007

TP39

A

1672-9129(2018)01-0015-03

梁圣. 基于RNN的试题相似度计算模型研究与实现[J]. 数码设计, 2018, 7(1): 15-17.

LIANG Sheng. Research and Implementation of Test-Items Similarity Computing Model Based on RNN[J]. Peak Data Science, 2018, 7(1): 15-17.

2017-11-05；

2017-12-17。

梁圣(1986-)，男，汉族，广西梧州人，硕士，湖南工业大学，研究方向：数据挖掘。E-mail:2646069240@qq.com