基于新安江模型的曲江流域水文模拟研究

谷 一， 王国庆， 郝振纯， 鲍振鑫， 陈煜良

(1.河海大学 水文水资源与水利工程国家重点实验室， 江苏 南京 210098； 2.南京水利科学研究院水文水资源与水利工程科学国家重点实验室， 江苏 南京 210029； 3.上海市建筑科学研究院集团， 上海 200032)

1 研究背景

20世纪70年代，河海大学赵人俊教授研制出了我国第一个大流域分布式概念性水文模型——新安江模型[1]。新安江模型在国内乃至国际均得到认可并得到广泛应用[2-5]，是中国少有的一个具有世界影响力的水文模型。新安江模型根据流域面积大小和研究需要可采用集中式模型和分布式模型来进行模拟，运用灵活多变，且其大多数参数具有明确的物理意义，有一定的物理机制[6]。目前，新安江模型已被广泛应用于洪水预报中[7-10]。

新安江模型在我国的应用日趋完善，周广刚等[11](1999)、朱求安等[12](2004)、唐俊龙等[13](2017)先后探讨了新安江模型在洒河流域、汉江江口流域、浙江白水坑水库等流域的适用性，结果表明新安江模型在我国绝大部分地区模拟效果良好。徐莎等[14]发现新安江模型在我国长江、淮河等湿润地区的模拟效果优于黄河、松花江等半湿润地区，尤其在最湿润的昌江流域可达甲等标准。水文模拟是开展环境变化影响的重要基础工作，本文采用新安江模型开展了曲江流域的水文模拟研究。

2 资料与方法

2.1 流域概况

曲江是珠江上游的一条主要河流，是南盘江西岸的一级支流，其位于云南省玉溪市和红河州的交界处。曲江流域地处低纬度高原区，地势东南低，西北高，山地、高原、盆地、峡谷交错分布，地形复杂多样[15]。属亚热带高原季风气候，立体化特征显著，冬春少雨，夏秋湿润[16]，多年平均降水量约为850 mm，且超过50%的降水量集中在6-8月份。流域内主要洪水类型为暴雨洪水，且受地形影响较为明显，多年平均年径流深为140～220 mm，降雨径流相关性良好。

本文选取的研究区位于曲江流域西山水文站以上区域，主要流经安化彝族乡、九溪镇、玉溪市、峨山彝族自治县、曲江镇，沿途有董炳河、九溪河、峨山大河等多条支流汇入，整条河流基本都在山区，植被茂密丰富，林地、草地和耕地分别占研究区面积的57%、13%、24%，城镇建设用地仅占4%，受人类活动干扰小。

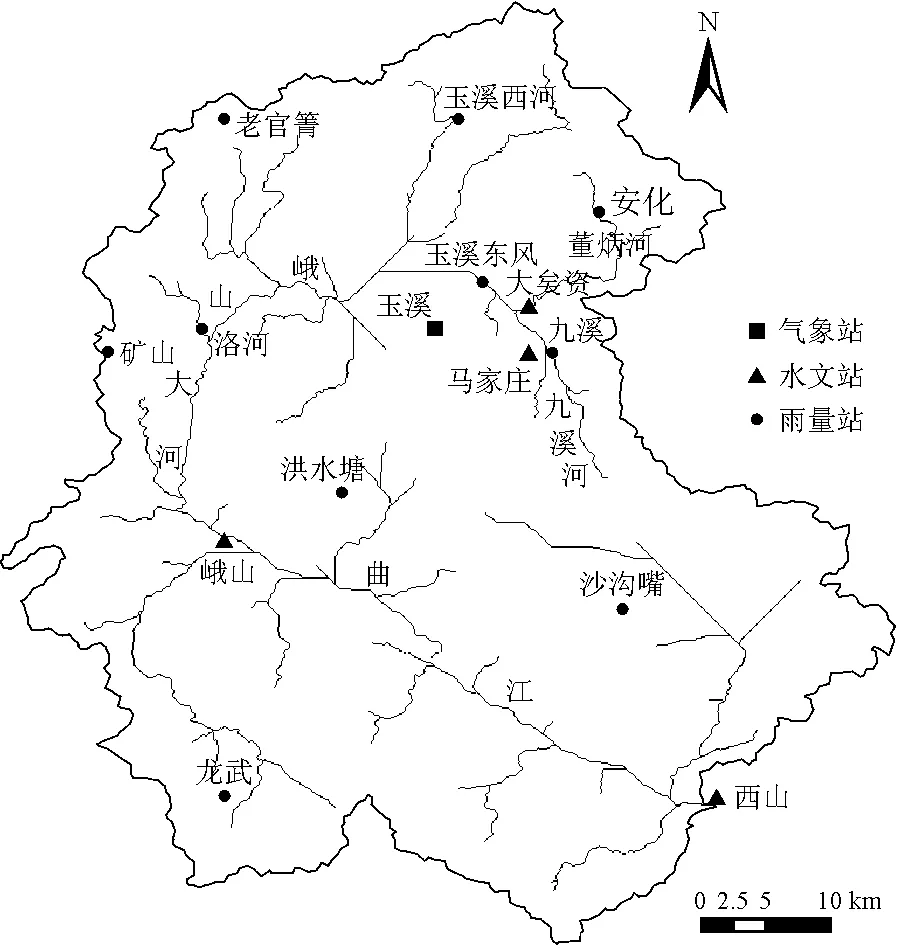
图1 曲江流域水系及水文气象站点分布图

曲江流域内气象站、水文站和雨量站的分布情况如图1所示，流域内有玉溪1个气象站，大矣资、马家庄、峨山、西山4个水文站，雨量站大多分布在峨山站以上。收集整理了流域内水文气象站点的逐日资料，表1给出了4个典型子流域的基本信息。

2.2 新安江模型

新安江模型主要基于蓄满产流理论，由蒸散发计算、产流计算、分水源计算、汇流计算4部分组成。本文采用的是3水源新安江模型，其蒸散发计算模块采用三层模式来分别计算上层、下层和深层地下水的蒸发量；产流计算模块采用蓄满产流模型，基于蓄水容量曲线来进行计算；分水源计算模块通过线性水库将总径流量划分为地表径流、壤中流、地下径流3个部分；汇流计算模块分为坡面汇流和河网汇流两个部分，通过马斯京根法或滞后演算法来进行计算[1]。

模型采用Nash-Sutcliffe效率系数和多年平均相对误差两个目标函数来表征模拟效果，其表达式如下：

(1)

(2)

3 模型分析结果

3.1 模型参数敏感性

本研究采用的三水源新安江模型共有16个参数，由于该模型涉及到的参数比较多，所以有必要对这些参数进行敏感性分析，从而提高模型率定的效率，缩短率定时间[17-18]。优选参数及其范围如表2所示。

表2 新安江模型参数及范围

上述模型参数中，KC、UM、LM、C为蒸散发计算模块的参数，WM、B、IM为产流量计算模块的参数，SM、EX、KG、KI为分水源计算模块的参数，CS、CI、CG、CR、LR为汇流计算模块的参数。

KC为水面蒸发量与蒸发皿蒸发量之比，控制着总水量平衡，UM、LM、C的增加会使得计算蒸发量增加，但UM、LM的影响相对有限，属于不敏感参数，C值对于湿润地区的湿润时期而言并不敏感，只对干旱期或半湿润地区产生较大影响。WM不敏感且不影响蒸发计算，蓄水容量曲线不变的情况下B与WM成负相关，IM可通过GIS技术直接测得，在本研究中不敏感。SM是敏感参数，其增加时会减少地表径流，KG、KI分别控制地下水和壤中流占总水量的比值，从而将总水量分成地表水、地下水和土壤水3层。CS、CI、CG为坡面汇流计算模块的参数，CR、LR为河网汇流计算模块的参数，本模型中均采用滞后演算法来进行汇流的计算，即基于线性水库的推移和坦化，来推求出口处的径流过程[19]。

3.2 水文过程模拟

受径流资料和蒸发资料的限制，本研究仅收集到大矣资站和马家庄站1982-1985、2006-2009年这8年的资料，以及峨山站和西山站1976-1985、2006-2015年这20年的资料。大矣资站和马家庄站采用3年率定，1年验证，峨山站和西山站采用7年率定，3年验证，表3统计给出了模拟结果。

由表3可以看出：(1)新安江模型模拟效果总体而言较好，率定期Nash效率系数均大于0.7，水量平衡误差控制在±5%以内，验证期效率系数均大于0.5，水量平衡误差控制在±15%以内。(2)西山站模拟效果最好，Nash效率系数最小为0.799，峨山站次之，Nash效率系数均大于0.7，且西山站和峨山站率定期的水量平衡误差均在-2%以内，验证期均在+10%以内，说明资料序列较长情况下新安江模型在曲江流域模拟效果良好。(3)大矣资站和马家庄站率定期的效率系数较高，验证期则较低，仅采用1年的资料对模拟结果进行验证，存在明显的偏差，较短的资料序列会严重影响模型的模拟精度。

图2给出了4个水文站实测与模拟的逐日流量过程对比，以便于更直观地分析新安江模型在曲江流域的模拟效果。可以看出：(1)4个水文站模拟结果良好，实测径流与模拟径流拟合程度较高，新安江模型在曲江流域能较好地模拟出径流过程的涨落。(2)新安江模型对不同丰枯年份径流的模拟存在着差异，对于丰水年的模拟效果明显优于平水年和枯水年，但其考虑的产汇流模式过于单一，对于洪峰的模拟不够精确。

4个水文站实测与模拟年径流量的散点图如图3所示，由图3可见：(1)4个水文站实测年径流量与模拟年径流量间具有良好的线性关系，相关系数均大于0.75。(2)大矣资站和峨山站相关系数最高，均超过0.9，峨山站点群最接近于1∶1线，说明峨山站模拟年径流量最接近于实测年径流量；大矣资站和马家庄站点群数量少，但均接近于1∶1线，处于合理范围内。

曲江4个水文站实测与模拟的径流量年内月分配过程如图4所示，可以看出：(1)实测流量与模拟流量的年内月分配基本一致，7-9月份为主汛期，一般8月份流量为全年最大，2-4月份为低流量期，4月份流量为全年最小，这与流域内的气候特征有很大关系，夏季降水多，更易形成降水，冬、春季节降水相对少，特别4月份时平均风速大，日照时数长，导致蒸发极大，故而流量较少。(2)汛期时新安江模型模拟值普遍偏小，非汛期则普遍偏大，分析认为曲江流域地处山区，汛期时多短历时强降水，降雨强度较非汛期大，因而并不完全进行蓄满产流。新安江模型模拟时仅用IM来概化不透水面积的产流，将强降水时超渗产流的部分直接视为蓄满产流计算，故汛期时模拟值偏小，为了减小水量平衡误差，非汛期时模拟值偏大。新安江模型能较好地模拟湿润地区的水文过程，但针对对包含短历时强降水的情况仍需改进。

表3 曲江流域4个水文站不同时期的模拟结果

图2 4个水文站实测与模拟日流量过程

图3 曲江4个水文站实测与模拟的年径流量比较

图4 曲江4个水文站实测与模拟月平均径流量

4 结 论

(1)新安江模型在曲江流域模拟效果总体良好，能够较好地反映出我国南方山区径流的特点，且对于丰水年模拟效果优于平水年和枯水年，但对汛期洪峰过程的模拟不够精确。

(2)基于单一的蓄满产流理论新安江模型存在着不足，其仅采用IM一个参数来概化流域内不透水面的超渗产流部分，如何考虑强降水时超渗产流的部分仍是新安江模型未来发展的重要方向。

参考文献：

[1] 芮孝芳, 凌 哲, 刘宁宁,等. 新安江模型的起源及对其进一步发展的建议[J]. 水利水电科技进展, 2012, 32(4):1-5.

[2] KHAN M H. Xinanjiang Model on Bird Creek catchment in USA.[J]. Pakistan Journal of Agricultural Research, 1993, 14(4):373-382.

[3] ZHU Dehua, PENG Dingzhi. Notice of RetractionComparison of the hydrological models in the Upper Medway Catchment, UK[C]// Sixth International Conference on Natural Computation. IEEE, 2010:3874-3877.

[4] 刘玉龙, 阮本清, 张春玲,等. 从生态补偿到流域生态共建共享——兼以新安江流域为例的机制探讨[J]. 中国水利, 2006(10):4-8.

[5] HAPUARACHCHI H A P, LI Zhijia, WANG Shouhui. Application of SCE-UA method for calibrating the Xinanjiang watershed model[J]. 湖泊科学(英文版), 2001, 13(4):304-314.

[6] 刘金涛, 宋慧卿, 张行南,等. 新安江模型理论研究的进展与探讨[J]. 水文, 2014, 34(1):1-6.

[7] 张 波, 马得莲, 包为民,等. 新安江模型在富水水库流域洪水预报中的应用[J]. 水电能源科学, 2010, 28(4):49-51+21.

[8] 胡宇丰, 安 波, 陆玉忠,等. 新安江模型在嫩江流域洪水预报中应用[J]. 东北水利水电, 2011, 29(8):41-45+72.

[9] 肖兴涛, 张鹏远, 张淑霞. 新安江模型在汤旺河流域洪水预报中的应用[J]. 黑龙江水利科技, 2012，40(1):41-43.

[10] 张漫莉. 改进的HBV模型与新安江模型在武江流域洪水预报中的应用比较[J]. 人民珠江, 2014, 35(1):34-37.

[11] 周广刚, 温立成, 侯国柱. 三水源新安江模型在洒河流域的适用性研究[J]. 水利水电工程设计, 1999(3):45-47.

[12] 朱求安, 张万昌. 新安江模型在汉江江口流域的应用及适应性分析[J]. 水资源与水工程学报, 2004, 15(3):19-23.

[13] 唐俊龙, 郝振纯. 新安江模型在浙江白水坑水库的适用性研究[J]. 水电能源科学, 2017，35(3):20-23.

[14] 徐 莎, 杨小柳. GR3模型和新安江模型在我国的对比研究[J]. 水文, 2015, 35(1):7-13.

[15] 谷桂华. 玉溪市暴雨洪水特性分析[C]// 中国水利学会2003学术年会，深圳：2003.

[16] 孙惠玲, 李天艳, 周晓娟,等. 近54年来玉溪市气候变化特征分析[J]. 云南师范大学学报(自然科学版), 2016, 36(5):67-73.

[17] 张利茹, 管仪庆, 叶 彬,等. 新安江模型参数敏感性分析的实证研究[J]. 水电能源科学, 2008, 26(5):16-17+30.

[18] 舒 畅, 刘苏峡, 莫兴国,等. 新安江模型参数的不确定性分析[J]. 地理研究, 2008, 27(2):343-352.

[19] 杨自坤, 孔 燕. 新安江三水源模型在横江洪水预报中的应用[J]. 水资源研究, 2010，31(1):36-38.