基于Kriging响应面模型的航空发动机套齿结构装配稳健性优化设计

权少宁

(西安航空职业技术学院 培训学院，西安 710089)

0 引言

在航空发动机中，套齿结构装配是有为重要的部件，其在工作过程中的转速比较高，对于其强度的需求也比较高。一般在实现强度有限元及流场分析之后，就要视线套齿结构的优化，从而降低结构的重量。相关人员表示，使用遗传算法能够实现结构优化。在套齿结构性能不断提高的过程中，在实现有限元分析过程中要充分考虑温度载荷，从而能够更加和工程实际结合。如果直接使用优化算法实现搜索，就会提高损耗，降低优化效率。所以在现代结构优化过程中，可以使用代理模型实现复杂有限元分析模型的近似，从而降低计算量，有效提高优化的效率。优化的算法一般都使用遗传算法实现，以此有效实现全局最优解。一般使用的代理模型包括Kriging响应面模型。目前对于发动机套齿结构实现有限元分析的时候，使用代理模型遗传算法实现的结构优化研究报道比较少。相关研究人员在实现压气机转子优化过程中实现套齿结构耦合强度计算，之后还对其进行了多项式模型遗传算法减重尺寸优化。多项式模型在使用过程中较为简单，并且容易寻优，但是需要大量的样本点。Kriging响应面模型具有多项式模型的优点，并且其需要样本点比较少，具有较高的拟合进度，所以其在相应工程领域广泛使用。基于此，本文就使用Kriging响应面模型实现航空发动机套齿结构的稳健性优化。

1 Kriging响应面模型的基本原理

Kriging属于线性回归分析的改进技术，其中主要包括非参数和线性回归两部分的内容。非参数的部分能够实现随机过程，假如随机过程是以高斯分布为基础，其中的协方差矩阵系数确定能够通过极大似然实现。Kriging在某个点实现模拟要根据此点周围已知的变量信息实现，简单来说，也就是利用此点在某个范围中实现信息加权线性组合实现此位置信息的估计。加权选择是利用最小化估计值误差方差实现确定，所以Kriging响应面模型就是最优线性无偏估计。那么，Kriging响应面模型主要包括随机分布和多项式的分布，Kriging响应面的模型形式通过进行表示，如式(1)。

y(x)=F(β,x)+z(x)=fT(x)β+z(x)

(1)

β属于回归系数，f(x)属于x变量中的多项式函数，其就相当于响应面发中多项式的形式。z(x)协方差的矩阵，如式(2)

Cov[Z(xi),Z(xj)]=σ2R[R(xi,xj)]

(2)

R(xi,xj)指的是n个样本点中任意两个样本点之间的空间相应方程，其能够决定模拟精准程度。并且相关研究人员也提出了多个可以选择的相应方程，其具有良好的计算效果，其中使用最为广泛的就是高斯相关方程，为式(3)

(3)

r(x)属于待测点与样本点之间相应的向量，通过以下式进行表示为式(4)。

(4)

其中的待测电估计值通过以下式进行表示为式(5)。

y=fTβ+rTR-1(Y-Fβ)

(5)

利用极大似然实现矩阵参数的确定，能够实现最优化问题的解决，以此对相应的参数进行确定，通过以上描述可以看出来，最优Kriging响应面模型创建问题也可以作为非线性无约束的优化问题[1]。

2 套齿结构的数值计算

2.1 分析确定性

选择某个航空发动机套齿结构为例，其最开始的装配间隙为100 μm，将我国机械工业标准作为基础，使用d级精度，创建有限元模型，如图1所示。

(a) 装配模型

(b) 内套齿

(c) 有限元模型

通过某个航空发送机典型的任务解剖图爬升阶段作为基础，就是将载荷的最大阶段成为危险点，对在负荷最大的时候尺侧间隙进行计算，得到的计算结果，如图2所示。

图2 计算得到的结果

图2通过计算结果可以看出来，危险点的最大尺侧间隙属于117.35 μm，比预测的间隙值要小，能够有效满足允许的最大值需求。

2.2 分析区间

在现实使用过程中，结构会受到材料属性、结构温度、载荷和力学性能的影响，所以得到的确定性结构无法满足结构可靠性需求，所以就要实现套齿间隙不确定的分析。本文所使用的区间变量为齿侧的间隙、温度、转速、密度等内容，将这些区间变量的范围进行确定，区间变量的取值范围，如表1所示。

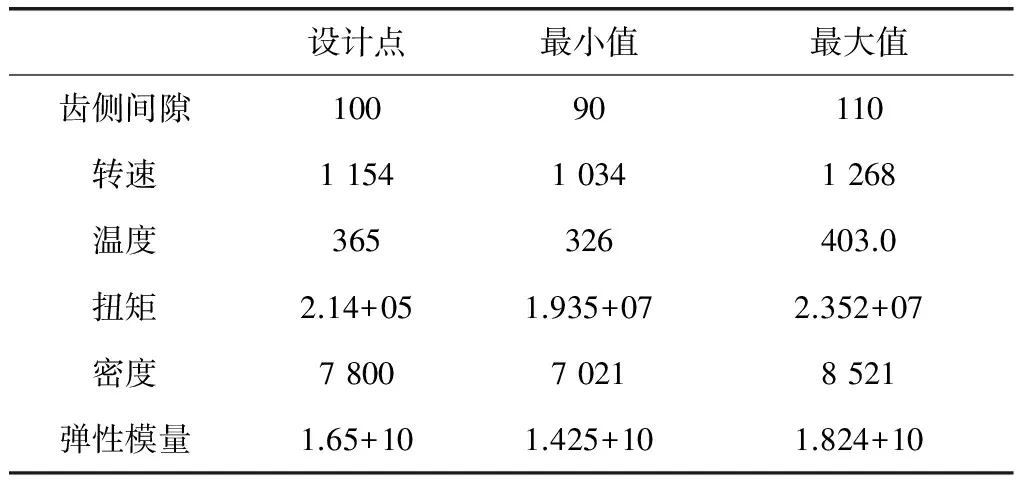
表1 区间变量的取值范围

其中的齿侧间隙属于设计变量，其他的区间变量属于不确定的参量。将设计点作为基础实现实验设计，通过设计得到多组样本点，通过Kriging响应面模型能够实现动态齿侧间隙和区间不确定参量、设计变量的创建，并且将其作为响应面模型。因为得到的多组样本点及响应面模型，将得到的样本点设计变量齿侧间隙作为确定量，其他的属于不确定参量，因为其属于区间变量，所以就要使用ANSYS有限元软件的响应面优化模块实现3千次抽样。在多个样本点输出响应最小值、最大值中得到12组典型的数据[2]，如表2所示。

通过表2可以看出来，在初始装配齿侧间隙为90-110范围中的时候，由于考虑到变量不确定性，结构动态一侧的间隙相应范围就是104.265 4-130.325 1。在初始设计点是100 μm的时候，齿侧最大的间隙值就是121.25 μm，其超过了120 μm，表示此种结构具有失效的可能性，所以就要完善最开始的装配间隙，从而使最大的间隙能够在120 μm以下。

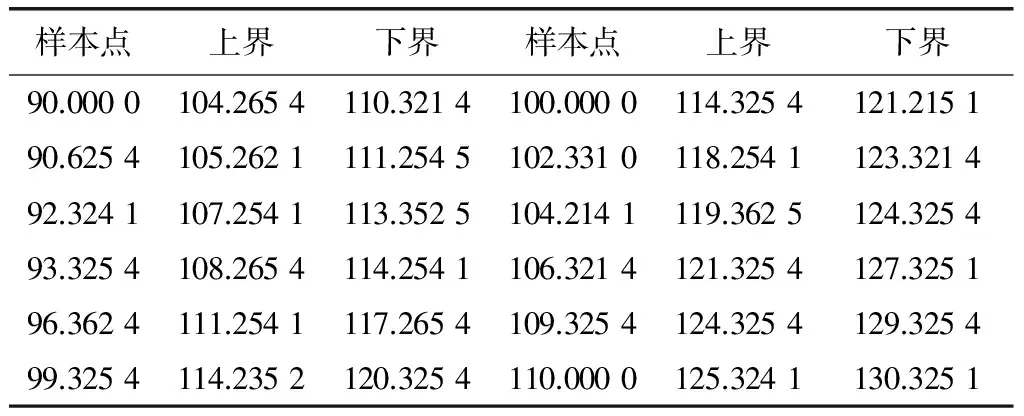
表2 典型样本点输出变量的上界和下界

2.3 套齿结构的稳健性优化

在优化过程中，使用Kriging响应面模型将初始的样本点通过试验的方法生成，一般使用的设计方法包括均匀设计、中心复合设计、正交设计和拉丁方设计。本文使用拉丁方设计实现，其属于以随机抽样试验设计的方法，其具有整齐可比性及均匀分散性的优势，能够有效满足较大采样空间和多因素的需求。Kriging响应面模型的优化流程，在具体优化过程中可以使用ANSYS软件实现，如图3所示。

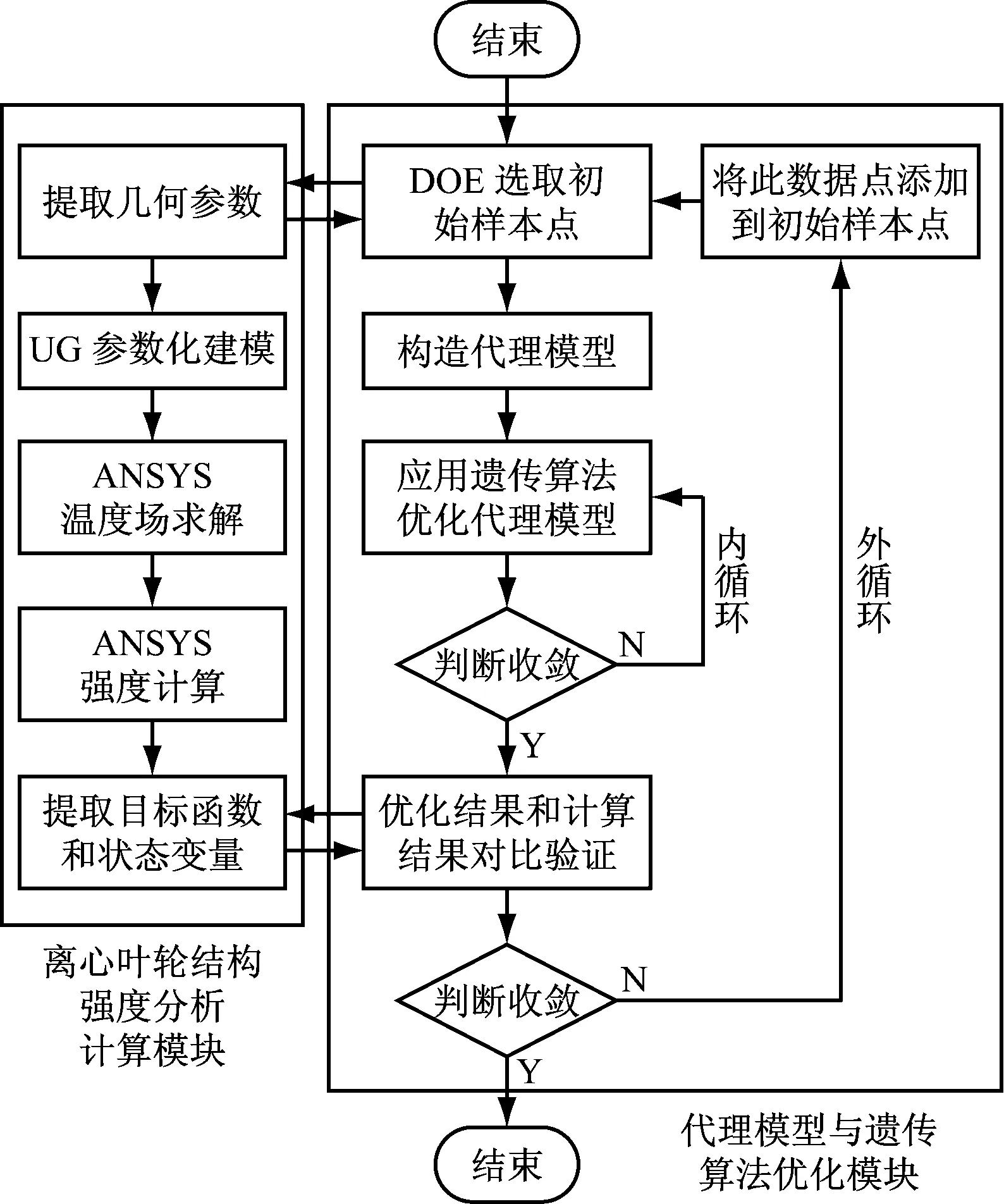
图3 Kriging响应面模型的优化流程

其一，利用拉丁方设计的方法实现初始样本点的生成，并且通过离心叶轮强度样本对模块进行分析和计算，从而能够有效得到最开始的数据点。

其二，通过初始的数据点实现Kriging响应面模型的创建。

其三，使代理模型能够转化成为遗传算法适应度函数，通过解码、编译、交叉等寻优搜索之后实现种群的优化，从而实现代理模型预测最优解。

其四，将代理模型预计的最优解和这个时候套齿结构装配强度数值实现计算，并且和真实的结果进行对比，如果能够满足收敛的条件，那么就表示实现了优化；如果无法满足收敛的条件，那么这个时候数值的计算数据点在最开始的数据点中添加，然后转回到第二步，重新创建代理模型，之后使用遗传算法优化更新之后的代理模型，最后收敛，从而实现全面的优化。

2.4 优化结果对比

预测的最优质和真实的计算值误差，如表3所示。

表3 预测的最优质和真实的计算值误差

通过表3可以看出来，在优化之后，其质量有所降低，最大的等效应力值和最大的径向应力值提高，能够有效降低强度校核的需求，并且还能够有效提高材料的使用率。套齿结构装配优化前后的截面对比，如图4所示。

图4 套齿结构装配优化前后的截面对比

图4中的虚线属于优化之后的截面，实线属于优化之前的界面，通过图2可以看出来，其优化的效果比较明显[3]。

3 总结

Kriging响应面模型在实现稳定性优化的过程中，能够充分的展现出自身在计算精度和计算效率方面的有效性，为了能够提高复杂结构的稳定性，其使用全新的计算方式实现，能够降低工程结构稳定性的时间。Kriging响应面模型技术具有较为精准的结构相应模型，从而为结构可靠性及稳定性的计算提供了全新的思路。

参考文献

[1] 毛连忠, 郝矿荣, 丁永生. 基于支持向量机的服装号型推荐模型建立[J]. 微型电脑应用, 2016, 32(3):1-4.

[2] 赖喜涛, 温卫东, 冯大俊,等. 基于Kriging模型的离心叶轮结构优化设计[J]. 沈阳航空航天大学学报, 2014, 31(4):17-22.

[3] 曹正策, 李晖. 基于Kriging响应面的活塞静态代理模型分析[J]. 湖北汽车工业学院学报, 2017, 31(1):23-27.