“拍照赚钱”的任务打包定价模型

西北政法大学 刘新洁 贺吉庆 谢佳利 刘婵

随着中国经济实力的不断增强、互联网的快速发展、企业成本的增加，网络群众的力量开始被越来越多的企业所重视。众包作为一种创新的电子商务模型，帮企业节约了大量的资金，在市场上占据着越来越重要的地位。“拍照赚钱”是一种基于移动互联网的自助式劳务众包平台，任务定价对用户能否获得满意的劳动报酬和降低成本(时间成本、经济成本)具有重要的影响作用。如果任务的标价不合理，就会造成有的地方会员争先选择，而有的地方却无人问津。本文基于这种现状将任务打包处理，以此吸引会员完成任务，降低企业成本。

1 模型的建立与求解

1.1 任务未完成的原因

本文首先运用Logistic回归建立二元选择模型来分析任务的纬度()、经度( )以及任务标价()对任务完成度的影响。假设事件发生的概率与不发生的概率之比称为事件的“发生比”，用来表示。则模型可写为：

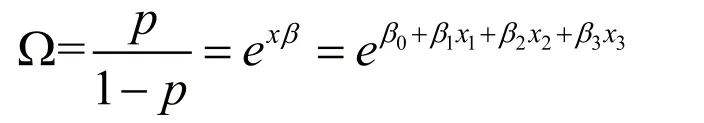
在上式中，解释变量 每增加一个单位时，发生比就变为原来的倍。当时，发生比会随着 的增加而增加；相反当＜0时，发生比会随着 的增加而减小。

接着依据极大似然法，借助SPSS软件进行回归分析，将835组数据代入Logistic模型中，对 、、 的值进行估计，可以得到表1、表2。

表1 模型整体显著性的Hosmer－Lemeshow检验结果

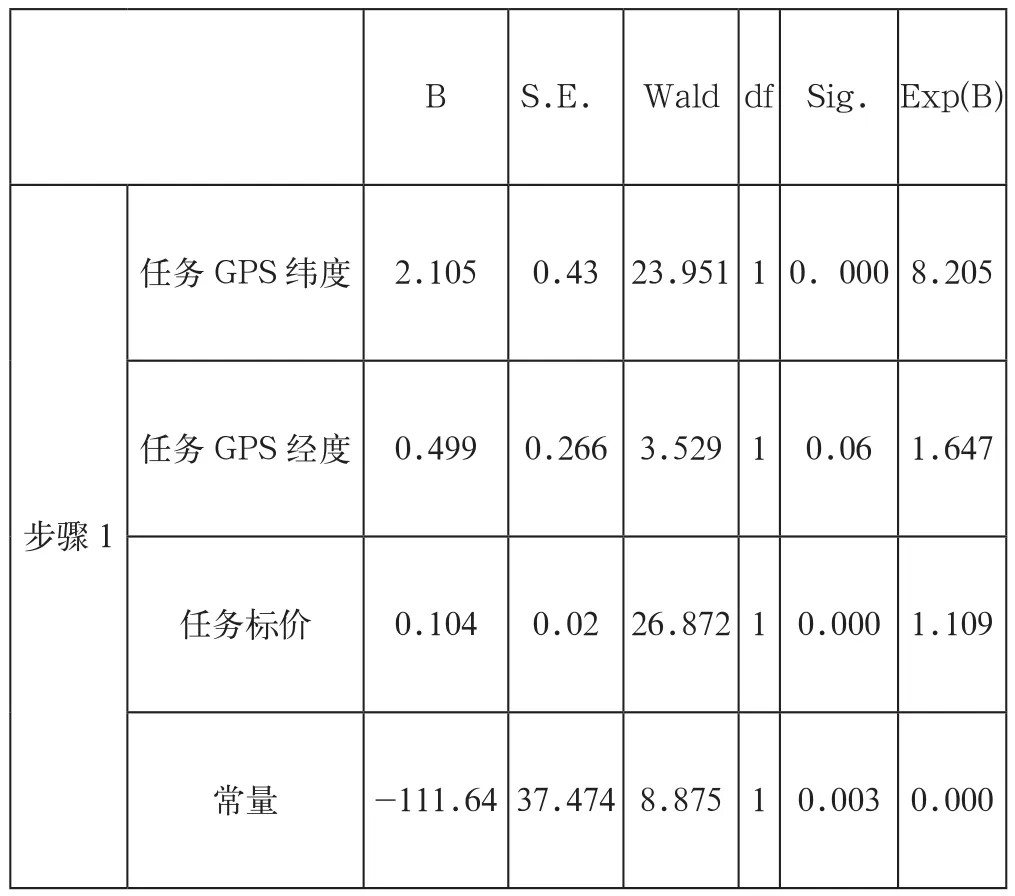
表2 回归系数估计值及其显著性检验结果

由表1中可以看到，Hosmer－Lemeshow卡方统计量为24.927，自由度为8，对应的P值为0.002＜0.01，所以得出的模型是整体显著的。从表2中的Wald统计量及其P值来看，任务GPS纬度和任务标价对应的P值小于0.01，通过了1%水平下的显著性检验；任务GPS经度的P值小于0.1，表明在10%的水平下显著。各个参数结果如下：

所以得出的任务的完成度与任务GPS纬度、任务GPS经度、任务标价的函数关系式为：

由表2中得出任务的纬度和经度每变动一个单位将分别导致发生比变为原来的8.205倍和1.647倍，由此可以推断出任务的地理位置是任务的完成情况的主要影响因素。

1.2 对区域进行k-means均值聚类

根据现实情况可以得出，有些任务商品由于地理位置比较集中，任务密集度高，而在此区域经济发展水平也较高，交通便利，人口密集度也高，所以会员在此区域的会员密集度也较高，会有更多的会员愿意完成任务，从而获取赏金。而相反在一些地理位置偏僻，交通不方便，会员密集度较低的区域，任务被完成的可能性就较低。为解决这种状况，提出对任务进行打包处理。

由于已完成任务的数量较多，故本文用SPSS软件进行K-means聚类算法下的任务打包。由于部分地区任务密集度太高，打包后的包内数量依旧较多，故又进行了二次拆包活动，最终设定了150多个任务包。部分聚类结果，如表3所示。

聚类的具体步骤如下：(1)将825个任务点分成150个初始类，并计算各初始类的中心坐标。(2)依据各个类聚对象的均值，计算任务两两之间的欧式距离d( ， )，将任务划入离中心最近的类中，然后重新计算中心坐标：

(3)重复上一步直到所有的任务都不能再分配为止，最短距离：

表3 部分任务的地区聚类结果

1.3 任务定价

现以第六组的打包任务的数据进行定价，通过定位分析发现这些任务位于会员密集区，故将六个任务进行打包可避免会员之间的争抢，也可以保证任务的完成度。

首先计算出这六个任务的中心点的经纬度为(22.599875°N,114.14385°E)，各个任务点到中心点的实际距离为：

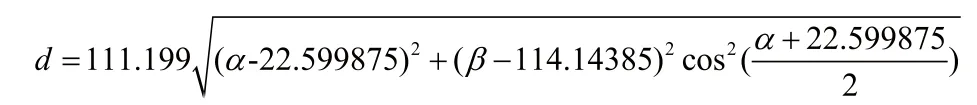
上式中 表示任务点的纬度，表示任务点的经度。

将任务点的经纬度代入后求得

“拍照赚钱”APP平台上发布的任务是商品，从经济理论中可知价值是凝结在商品中的人类无差别的劳动，因此对于那些消耗劳动量越大商品，价格理应越高。由供求定理可得，在会员密集度较高的地区，假定任务的数量是确定的，不同的任务相应的价格也不一样。此时会员对任务的需求大于任务本身的供给数量，造成会员对任务的争相选取。在这种情况下，就产生了“卖家市场”，只要发包方将任务的定价定的高于会员所能接受的最低价格，那么就总会有一些人为了生计和生活接受任务并将其完成，保证了任务被完成的可能性。而在任务地理位置较远、会员稀疏的地区就形成“买家市场”，此时应该将任务价格定高一些，从而吸引会员的活跃性。由于每个任务的经纬度及会员密度之间存在着显著的差异性，这些任务点可以看成是以中心点为圆心的一个环形区域，任务点与中心点的距离每增加0.1km，任务的价格将在原有的基础上增加0.1元。则打包后的任务组合定价为：

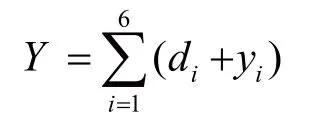
在此基础上运用排水工程中的折减系数，其值是一个小于或等于1的数。对打包任务总价进行折减，根据调查发现折减系数k为0.95时最为恰当，此时的价格会员和发包方都可接受。因此折减后的打包价格为

而打包前的任务成本为，经比较可得则可以得出这种先将任务的标价提高，给会员造成一种心理上的错觉，可成功激发会员的积极性，然后再运用折减系数进行总价格的折减，合理、巧妙地节约了发包方的成本，同时提高任务的完成率，符合企业优化的需求。

1.4 任务的影响分析

将打包后的任务数据代入任务完成度与任务经纬度、定价之间的Logistic回归方程：

得出：P=0.7713。

由于任务的完成率=已完成的任务/总任务，通过计算可得知打包前的任务完成率为0.6251＜0.7713，故将任务进行打包重新定价的效果显著，此方案切实可行。

2 结语

本文通过建立数学模型，分析出任务的地理位置是影响任务完成率的重要影响因素，在此基础上对地区进行聚类分析，将距离较近的任务进行打包，并运用经济学知识求得了打包价格，证明了打包发布可以达到刺激会员积极性，提高任务完成率，降低发包方成本的目的。

参考文献

[1] 全国大学生数学建模竞赛组委会.2017高教社杯全国大学生数学建模竞赛(CUMCM)题目B题[EB/OL].http：//www.mcm.edu.cn/，2017-09-14.

[2] 李继成，李萍，赵小燕.数学实验[M].北京：高等教育出版社，2014.

[3] 朱建平，方匡南.SPSS统计分析与应用[M].北京：首都经济贸易大学出版社，2013.