基于多类型励磁系统对电磁磁选机磁场特性、选矿指标的分析

李作敏，张颖新，于岸洲

(1.中国地质科学院郑州矿产综合利用研究所，河南 郑州，450006；2.国家非金属矿资源综合利用工程技术研究中心，河南 郑州，450006)

电磁选机以电场产生磁场的基本原理，通过一定的磁系设计与机械结构实现矿物分选[1-2]。近几十年来，电磁磁选机迅速发展，为弱磁性矿物分选提供了高效的设备支撑，代表性的电磁磁选机有琼斯高梯度磁选机、立环高梯度磁选机与浆料高梯度磁选机[3-4]，供电电源作为设备磁场的统一配置，激励磁场的生成，而激励磁场的励磁系统有多种组成形式，本文考察多种励磁形式下的磁场差异性，进而检验不同磁场特性对矿物分选效果的影响。

1 电磁磁选机实验室模型的设计

以小型电磁铁为研究对象，配置不同的励磁系统，考察其磁场特性的不同，设计一台最高磁场感应强度为1 000 mT的电磁铁，确定两磁极头间距为12 mm，线圈包裹在连接磁极头的磁轭处，有利于磁场强度最大化利用[5]，线圈选用直径为2 mm的漆包铜线，考虑刷漆与导线间隙，每根导线按照4 mm计算，应用磁位降法[2,5-6]确定磁轭尺寸与线圈匝数，线圈总匝数270匝，横向30匝，长度为120 mm，纵向9匝，长度为36 mm；磁轭为长方体结构，横向上磁轭的长127 mm，宽60 mm，其两侧对称，下磁轭长390 mm，宽60 mm；纵向磁轭长200 mm，宽60 mm。电磁铁外形结构如图1所示。

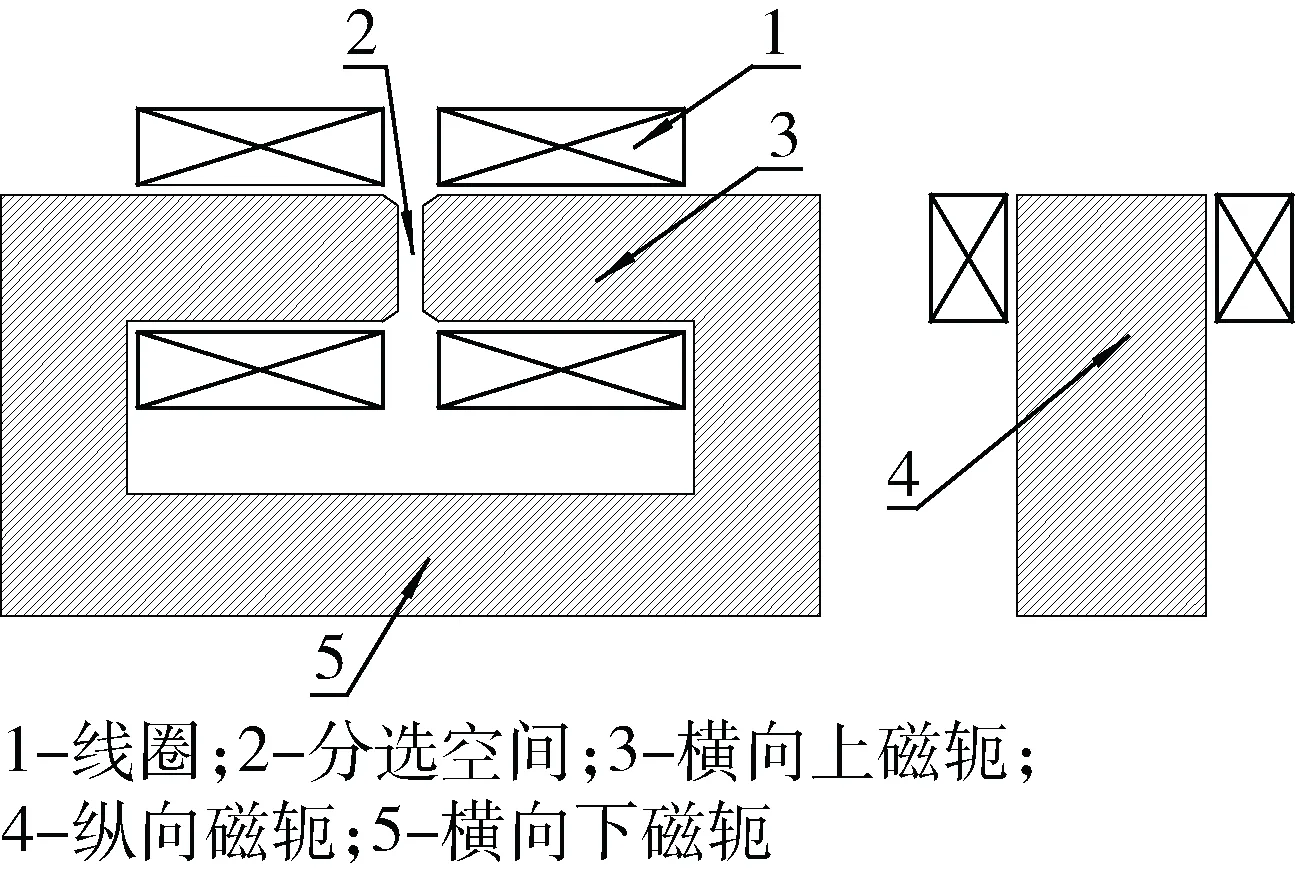
图1 电磁铁外形结构

2 多类型励磁系统的研究

2.1 直流稳压电源励磁系统

选用能提供最大输出电流20 A，电压14 V的直流稳压电源为电磁铁的励磁装置，正常供电后，调节输出电流的大小，使磁场感应强度为400 mT。利用高频率高斯计CH-1600探头放置于两端磁极头间隙处监测磁场瞬时变化，应用9针串口(RS232)与计算机相连，接收实时监测数据，把数据导入至Origin分析整理，数据见图2。

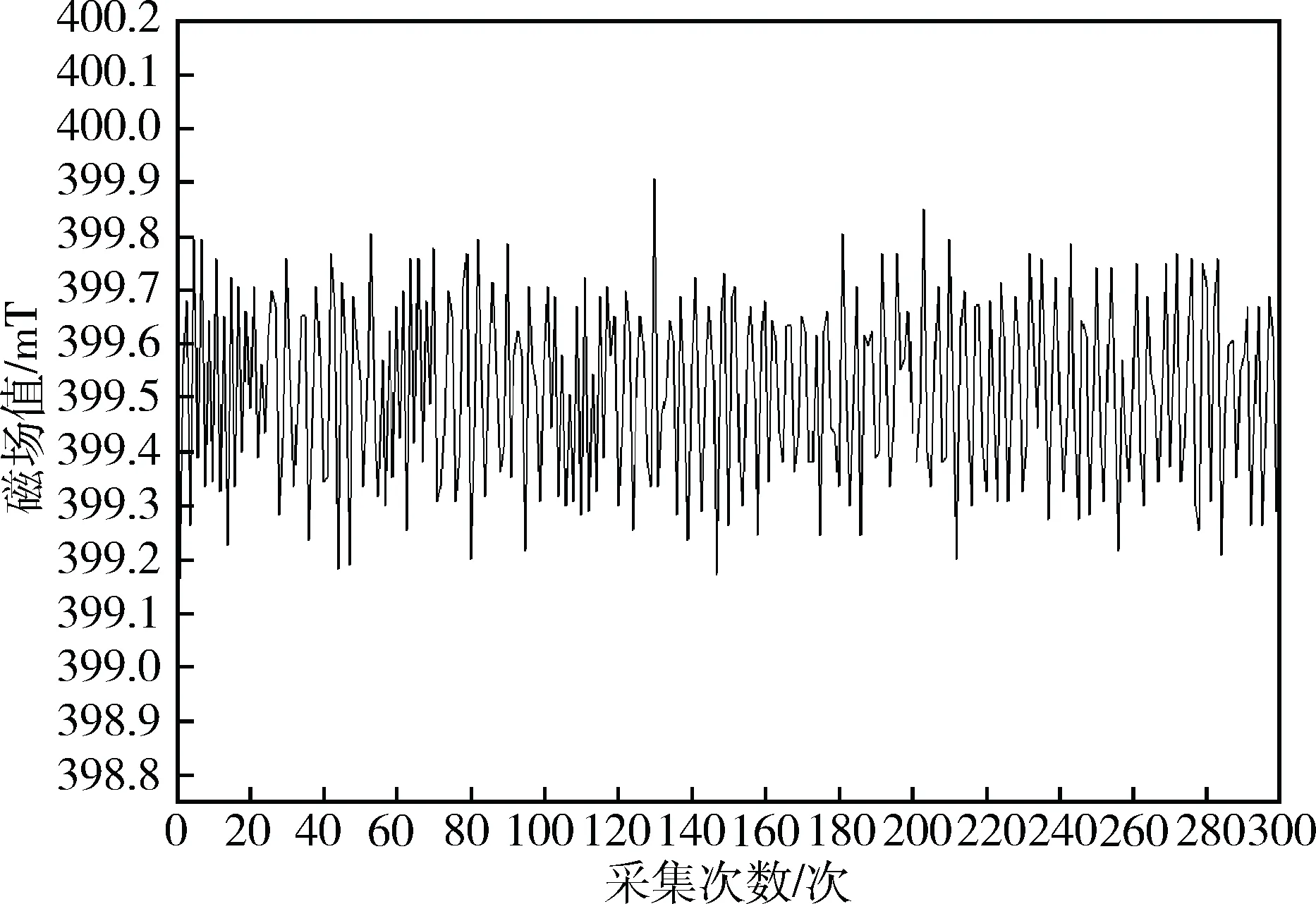
图2 直流稳压电源生成磁感应强度分布图

磁场波形随着电流输入波形的波动而发生瞬时变化，磁感应强度在399.5 mT浮动，最大值为399.9 mT，最小值为399.2 mT，磁感应强度的波动范围在0.7 mT内，直流稳压电路产生非常稳定的磁感应强度。

2.2 移相触发调压式励磁系统

采用移相触发电路作为电磁铁的励磁系统，观察电流波形的变化对其所产生磁场特性的影响，其电路接线方式如图3所示。

图3中虚线部分左一为半控移相调压电路，只能调节二分之一电压波形，其变压器输出端a接入调压装置输入端1、2和3并联使调压装置形成回路与整流装置的c端串联，变压器输出端b与整流装置d串联后形成主回路系统。触发器的220与ON端外接一个220 V交流电给触发器供电，其公共端、主输入与+5V的端子分别与电位器的o、p、q相接，实现手动功率调节功能，触发器的两个触发端子分别于调压可控硅G1、K1相接完成触发。按照图3半控移相调压接入电磁铁，测定磁感应强度分布，如图4所示。

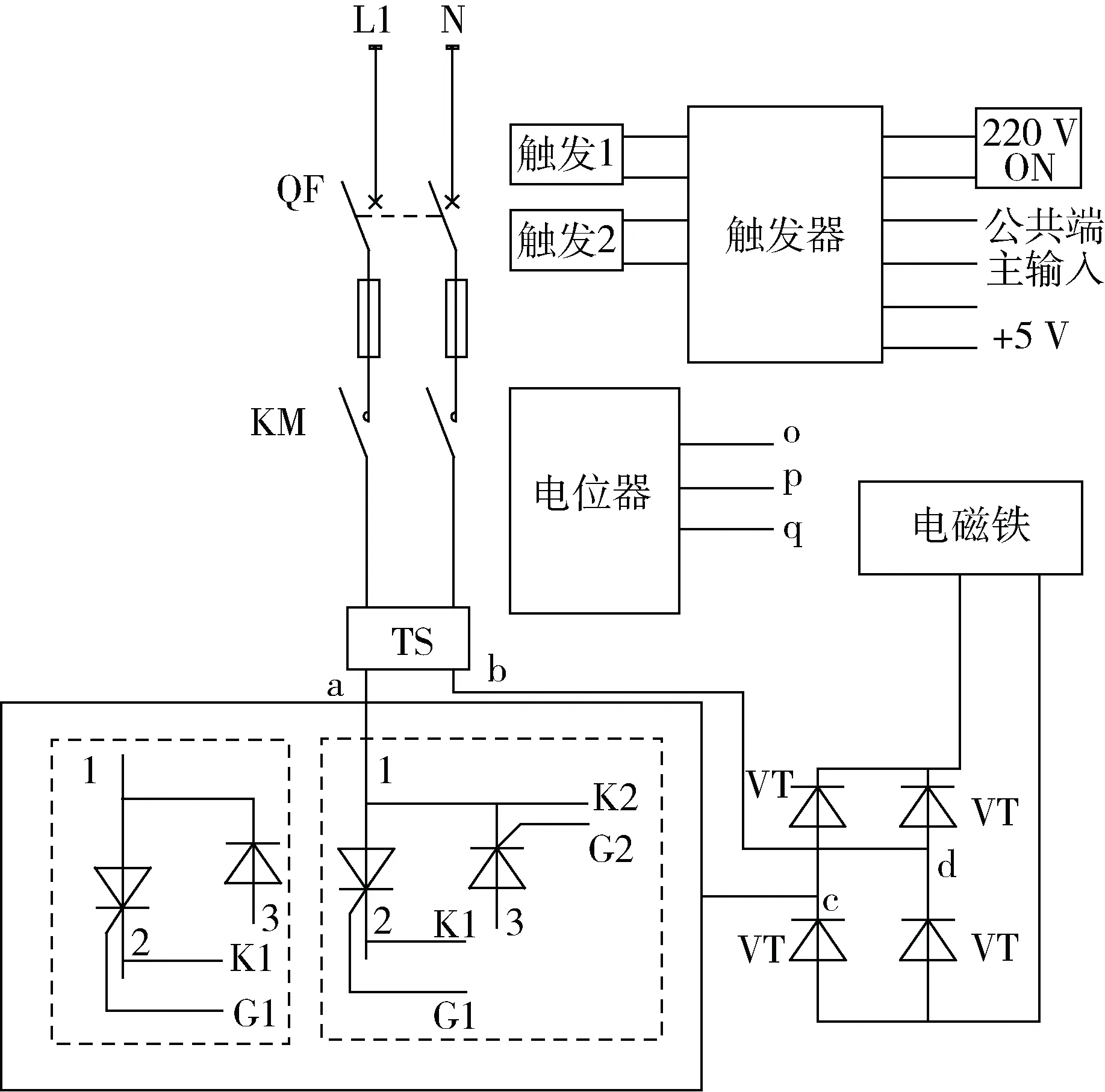
图3 电磁铁励磁系统电路图

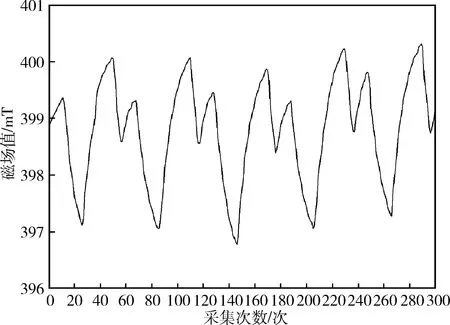
图4 半控移相调压控制电路生成磁感应强度分布图

图4中每两个正弦波组成一个周期，相邻正弦波的磁场感应强度峰值相差1 mT，磁感应强度最大值为400 mT，最小值为397 mT，相差3 mT，每个周期的波动在4 s左右，确定其为较稳定的磁感应强度分布[7]。

图3中虚线框左二为全控移相调压电路，其调压端子K2、G2与触发器的触发端子2相接完成控制[8-10]，其他电路与半控移相调压一致，其周期内上下波形均可调节，调试完成后得到的磁感应强度波形如图5所示。

图5 全控移相调压控制电路生成磁感应强度分布图

图5中为两个完整的周期，与半控移相调压控制电路相比，每个周期波形可控部分增多，三个波峰两个谷值，磁场感应强度最大值为411.5 mT，最小值为406 mT，相差5.5 mT。与半控移相调压电路相比，磁感应强度波动值增加了2.5 mT。

2.3 过零触发调压式励磁系统

过零触发调压电路的调压特点是在一定的时间周期里，根据所设定的电压值，瞬间关断或开启数个完整周期的电压，所呈现的通电电压波形依然是完整的周期波[11]，过零触发调压式电路接线方式与移相触发调压电路一致见图3，不同的是置换触发器中触发板的DIP开关[12]，第三位功能键OFF变为ON，使之为过零触发方式[13-14]。测定过零触发调压控制电路产生的磁场感应强度见图6。

由图6可见，每个磁场波形为完整的正弦波，波峰值大小在一定的时间内呈有规律的变化，磁感应强度波动频率较大，每两个相邻周期约隔1 s，磁感应强度最大值为415 mT，最小值为396.5 mT，相差18.5 mT。为了进一步确定磁场波动与电流的关系，对过零触发半控电路变换为过零触发全控调压，考察组成的励磁系统所产生的磁场特性，见图7。

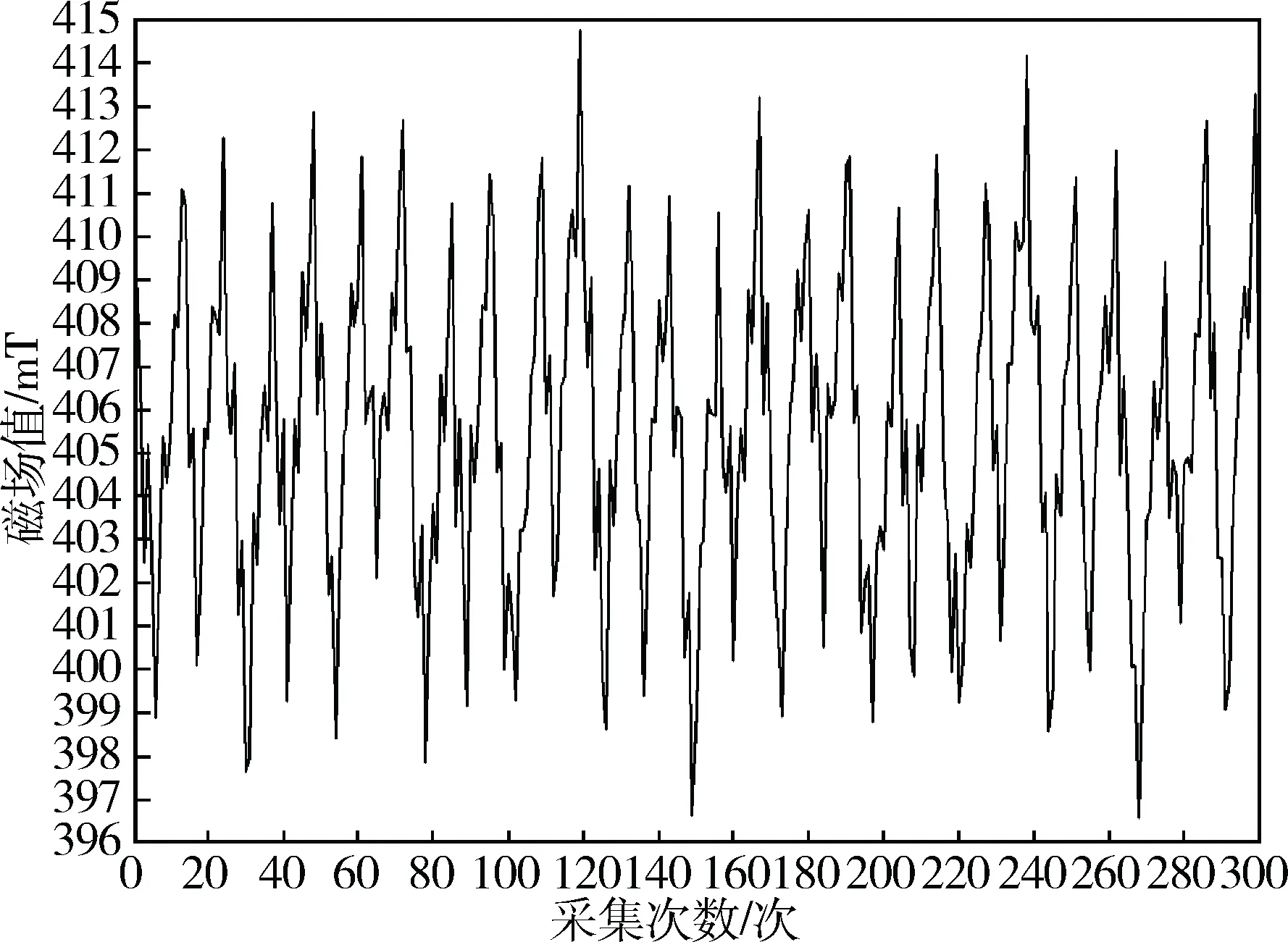
图6 半控过零触发调压电路生成磁感应强度分布图

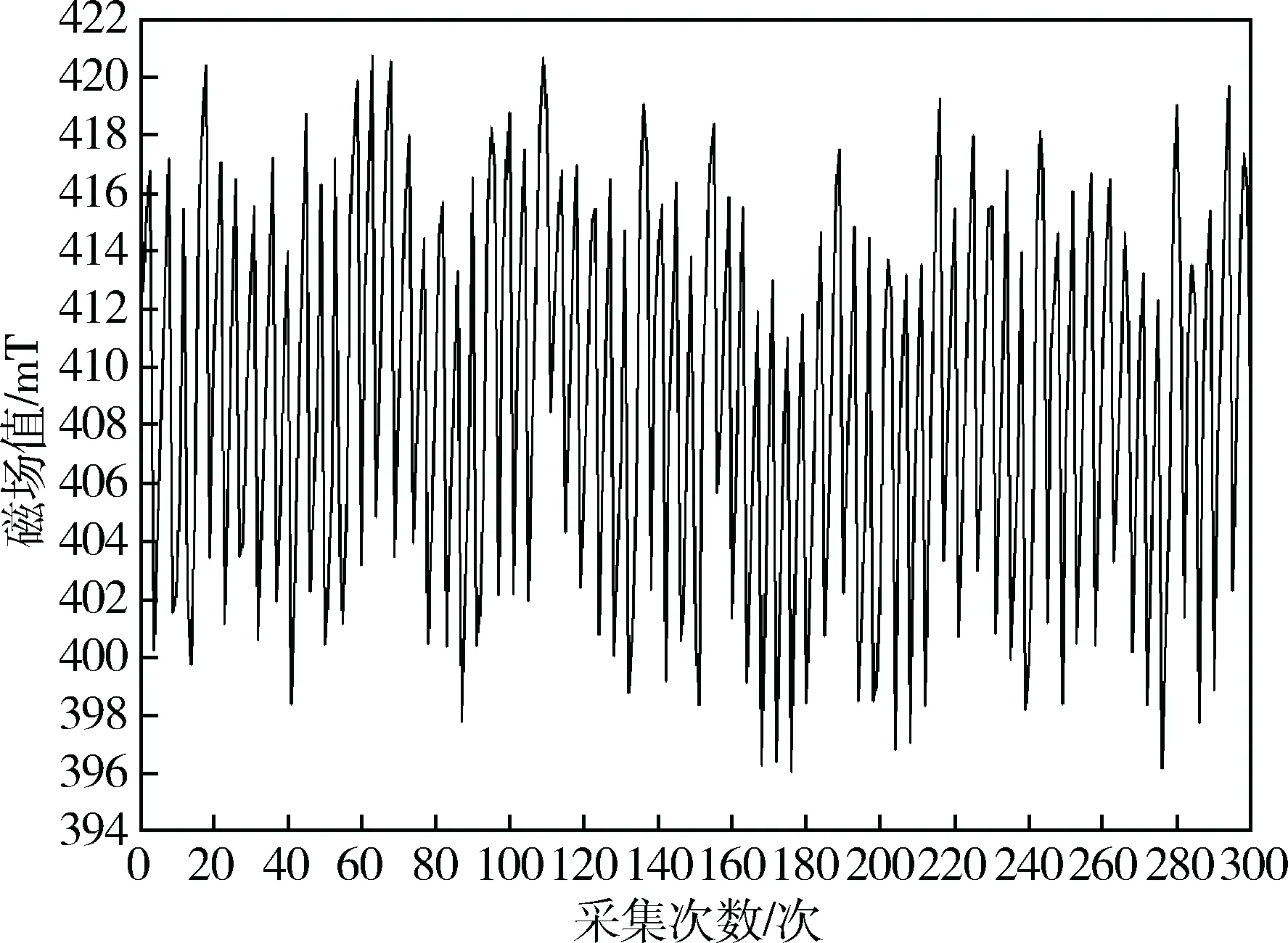
图7 全控过零触发调压电路生成磁感应强度分布图

全控过零触发调压系统所产生的磁场波动频率进一步增大20次/s的采集点有5个完整的周期，平均每两个相邻的波峰之间相隔约0.2 s，其磁感应强度最大值为421 mT，最小值为396 mT，相差25 mT；每5个周期波呈有规律性的逐渐降低。

由此可得出结论：直流稳压电源产生的磁场较稳定，移相调压控制电路产生的磁场强度有微小波动，而过零触发控制电路产生的磁场波动范围较大，频率较高。可见不同的励磁系统产生具有不同特性的磁场，电压输出波形与输出频率直接影响所产生的磁场特性，磁场波动范围与波动频率因其不同而发生改变，磁选机的励磁系统不是单一的供电系统，其直接影响输出磁场模式。在磁选机选型中，往往只考虑磁场强度的强弱，而忽略磁场特性对选矿指标的影响。

3 多类型励磁系统对矿物分选的影响

根据不同的励磁系统产生不同特性的磁场，考察不同励磁系统对矿物分选的影响，电磁铁无法直接进行矿物分选，选择上述设计中产生磁场特性差异较大的三种励磁系统(直流稳压励磁系统、全控移相调压式励磁系统与全控过零调压式励磁系统)配置给周期式高梯度磁选机Ф200，对原矿铁品位(TFe)为19%，-0.075 mm占62.7%的磁铁尾矿进行分选，试验流程如图8所示，试验结果见表1。

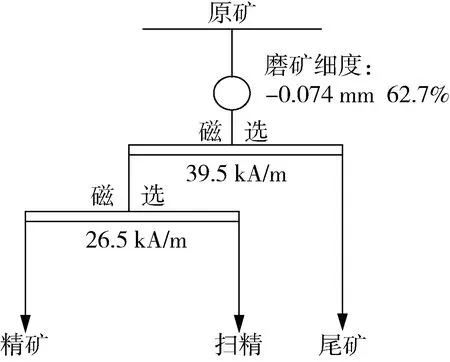
图8 不同励磁系统应用试验流程图

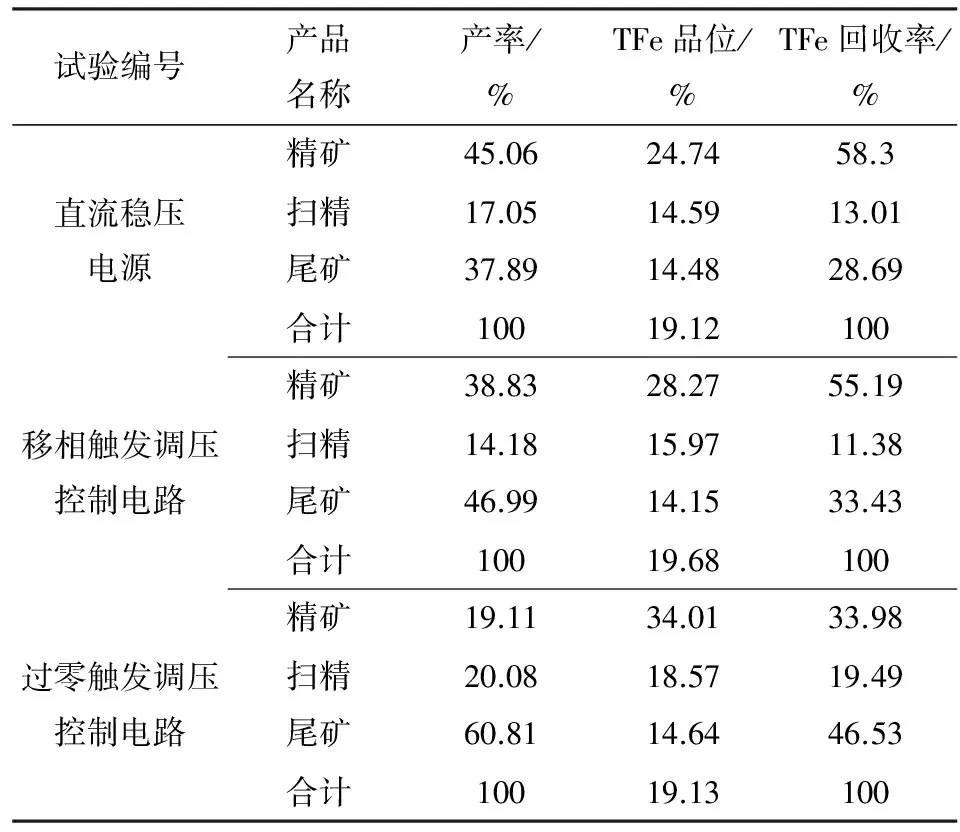
试验编号产品名称产率/%TFe品位/%TFe回收率/%直流稳压电源精矿45．0624．7458．3扫精17．0514．5913．01尾矿37．8914．4828．69合计10019．12100移相触发调压控制电路精矿38．8328．2755．19扫精14．1815．9711．38尾矿46．9914．1533．43合计10019．68100过零触发调压控制电路精矿19．1134．0133．98扫精20．0818．5719．49尾矿60．8114．6446．53合计10019．13100

由表1可知，分别应用三种励磁系统匹配的磁选机对磁铁矿作磁选试验，直流稳压电源励磁系统分选的精矿TFe为24.74%，移相触发调压控制电路分选的精矿TFe为28.27%，过零触发调压励磁系统分选的精矿TFe为34.01%，可见精矿品位随着磁场震荡频率与磁场波动范围的增大而提高。矿物被分选的过程中，磁场强度波动范围与波动频率的加大，磁性颗粒完成被磁场吸附→松散→吸附的多次分选过程[15-16]，有效地排除了磁性矿粒中夹杂的非磁性矿物，提高了精矿品位[17]。

4 结 论

1) 不同励磁方式产生具有不同特性的磁场强度。励磁系统为直流稳压电路时，其产生的磁场波动范围极小，可称之为稳定磁场；当励磁系统的控制方式移相触发调压电路，其产生的磁场强度范围变大，并随触发方式的不同形成波动幅度强弱变化的磁场；过零触发调压电路组成的励磁系统产生的磁场波动周期小，波动范围最大，波动频率最高。

2) 应用三种励磁系统做磁铁矿选矿试验，直流稳压型励磁系统分选精矿品位最低，回收率最高；过零触发型励磁系统分选精矿品位最高，回收率最低。电磁式磁选机的励磁系统不能单一理解成为普通机器供电的供输电系统，当供给与调压方式发生改变时，其产生的磁场特性也发生相应的变化，并影响矿物分选指标，可见励磁系统是衡量电磁式磁选机性能的重要因素之一。

参考文献

[1] 赖卫平.周期式高梯度磁选机磁系设计探讨[J].有色设备,1990(3)：14-17.

[2] 彭会清.磁选机磁场解析法研究及应用[D].武汉：武汉理工大学,2006.

[3] 梁树林.周期式高梯度磁选机[J].中国陶瓷,1984(3):47-48.

[4] 吕波,骆振福.国内磁选机的发展现状与趋势[J].矿山机械,2011,39(7):1-4.

[5] 孙仲元.电磁磁选机磁系设计[J].有色金属:冶炼部分,1975(4):19-25.

[6] 孙仲元.选矿设备工艺设计原理[M].长沙:中南大学出版社,2006.

[7] 王常任,高明炜.电子计算机在磁选设备磁路计算中的应用[J].金属矿山,1985(2):36-50.

[8] 孙亚辉.电动操作隔离开关控制回路设计分析与应用[J].电气技术,2010(9):66-70.

[9] 泰州电压调整器厂技术组.接触式调压器最大短路损耗时横臂的位置[J].变压器,1975(5):45-46.

[10] 魏骥云.接触式调压器的改革[J].变压器,1981(6):8-9.

[11] BYKAT A.Automatic generation of triangular grid:I-subdivision of a general polygon into convex subregions. II-triangulation of convex polygons[J].International Journal for Numerical Methods in Engineering,1976(10):1329-1342.

[12] 张南山.基于DSP的大功率数字电源产品化研究[J].电源世界,2008(2):29-33.

[13] 吕天文.中国线性与开关电源的现状及其发展趋势分析[J].电源世界,2011(12):8-9.

[14] 林辉,王辉.电力电子技术[M].武汉:武汉理工大学出版社,2002.

[15] KLEVETS N L.Optimal design of magnetic systems[J].Journal of Magnetism & Magnetic Material,2006,306(2):281-291.

[16] CHEN D Y,WOLDEN J P.Application of transistor emitter open turn off scheme to high voltage power inverters[C]∥IEEE Power Electronics Specialists Co inference.1981.

[17] 杨盛业.对磁选指标影响因素的分析[J].钢铁,1964(3):22-26.