土体耦合蠕变渗流模型在隧道沉降数值模拟中的应用

地铁隧道纵向不均匀沉降不仅会影响地铁隧道的结构安全,同时,也会影响列车行进。上海市地铁隧道开挖及下卧土层以粉质黏土或淤泥粉质黏土为主,无论是隧道开挖后的静置期还是运营期,这类软土的蠕变及渗流固结都是导致隧道后期沉降的重要因素。目前,关于地铁隧道的沉降研究有理论分析及数值模拟两种不同的手段。对于理论分析而言,诸如以志波由纪夫为代表的弹性地基梁模型和以村上博智、小泉纯为代表的梁-弹簧模型[1-2]是常用的隧道纵向沉降分析的方法,而数值模拟方面则以有限元数值分析为主[3-4]。本文将依托上海市地铁13号线华夏中路段工程,在弹塑性模型的基础上补充建立一个考虑土体蠕变和渗流耦合的数值模型,模拟计算隧道开挖期及开挖后静置期隧道的沉降。

1 工程概况

本次数值分析的隧道位于上海市轨道交通13号线华夏中路段,隧道埋深15～25 m不等,外径6.2 m,衬砌壁厚0.35 m。隧道剖面的土层分布见图1。总的来说,第4层和第5层土厚度较厚,覆盖面积大,是地铁隧道穿越的常规土层,同时，由于其较高的塑性以及渗透性,这两层土体由固结和蠕变引起的沉降也远大于其他土层如填土层等,是工程关注的重点。

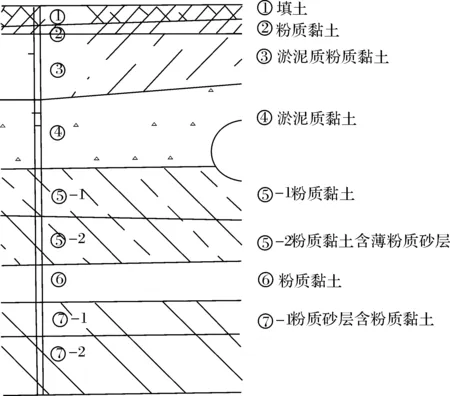
图1 土层地质分布图

2 土体耦合蠕变渗流模型

2.1 塑性模型

塑性模型选取Drucker-Prager模型。

2.1.1 屈服面

Abaqus中Drucker-Prager模型的塑性屈服面的子午线有线性、双曲线及指数型三种,本文考虑子午线为线性的Drucker-Prager屈服面[5]。

F=t-ptanφ-c=0

(1)

2.1.2 流动法则

采用双曲线塑性流动势函数

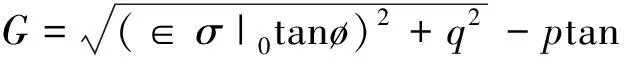
(2)

式中:ø是高围压状态下在p-q平面的剪胀角；

∈为偏移率;

σ|0为初始屈服应力。

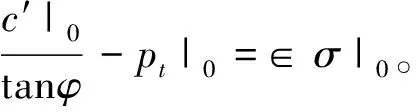
2.2 时间硬化蠕变模型

采用Abaqus有限元模型附带的时间硬化准则,其表达式如下：

(3)

式中：εcr为等效蠕变应变；

σcr为等效蠕变应力；

A、m、n为与时间硬化相关参数,由实验拟合或经验取值；

t为蠕变时间。

其微分方程表达式如下

(4)

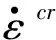
2.3 渗流模型

2.3.1 平衡方程

(5)

式中:t为面力;

f为体力;

δε为虚位移;

δu为虚应变;

Dep为弹塑性矩阵;

β为由毛细压力和饱和度之间的吸湿或干燥试验曲线确定;

sw为饱和度;

pw为孔隙水压力;

KS为固体颗粒压缩模量;

m=[1,1,1,0,0,0]T。

2.3.2 连续方程

(6)

式中:k0为初始渗透系数张量与水密度乘积；

kr为比渗透系数；

g为重力加速度矢量；

n为孔隙度；

kw为水体积模量,其他同上[8]。

3 有限元模拟计算分析

3.1 计算参数确定

在文献[4]中关于各类土体蠕变参数拟合的基础上,根据上海地区勘测土层物理力学性质参数表,并对相近力学参数的土层作合并简化,整理出建模采用的各土层计算参数见表1。

3.2 有限元模型

结合实际工程,利用有限元软件Abaqus,考虑蠕变渗流耦合模型计算。土体及衬砌都采用带孔压的平面应变单元CPE4P。有限元模型高取60 m,横向取100 m,考虑对称实际建模横向50 m。隧道埋深15 m,外径6.2 m,衬砌厚度0.35 m,衬砌不考虑塑性阶段,衬砌和周围土体摩擦接触,法向为硬接触,切向接触系数根据具体情况取0.2～0.4不等。

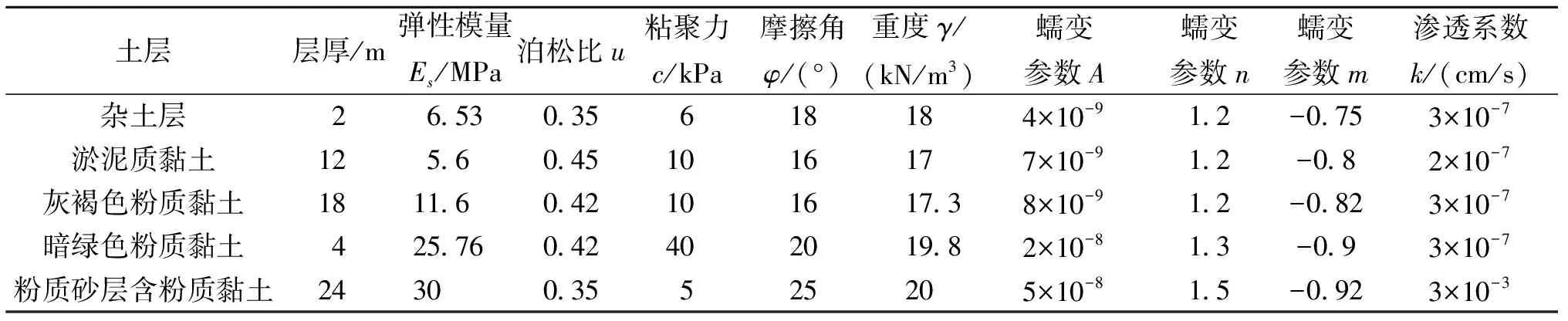
表1 土层计算参数表

3.3 沉降过程模拟

本次数值模拟沉降过程包含施工过程沉降及静置过程沉降,具体如下：

1) 考虑盾构机挠动带来开挖区土体损伤(假设开挖区土体弹模变为初始值的60%);

2) 在开挖区土体周围添加衬砌;

3) 移除开挖区土体,完成隧道开挖;

4) 静置1年时间,讨论蠕变以及隧道底部渗水引起的沉降。

由于开挖历时相对较短,不考虑开挖阶段的排水固结(主固结沉降)及蠕变(次固结沉降)。整个静置过程持续31 536 000 s,即模拟13号线施工完成后到运营期间静置1年时间。

3.4 计算结果分析

从图2可以看出,盾构隧道施工完成后,隧道两侧中部附近塑性区最严重,这一部分塑性破坏也是导致施工过程中隧道沉降的主要原因。

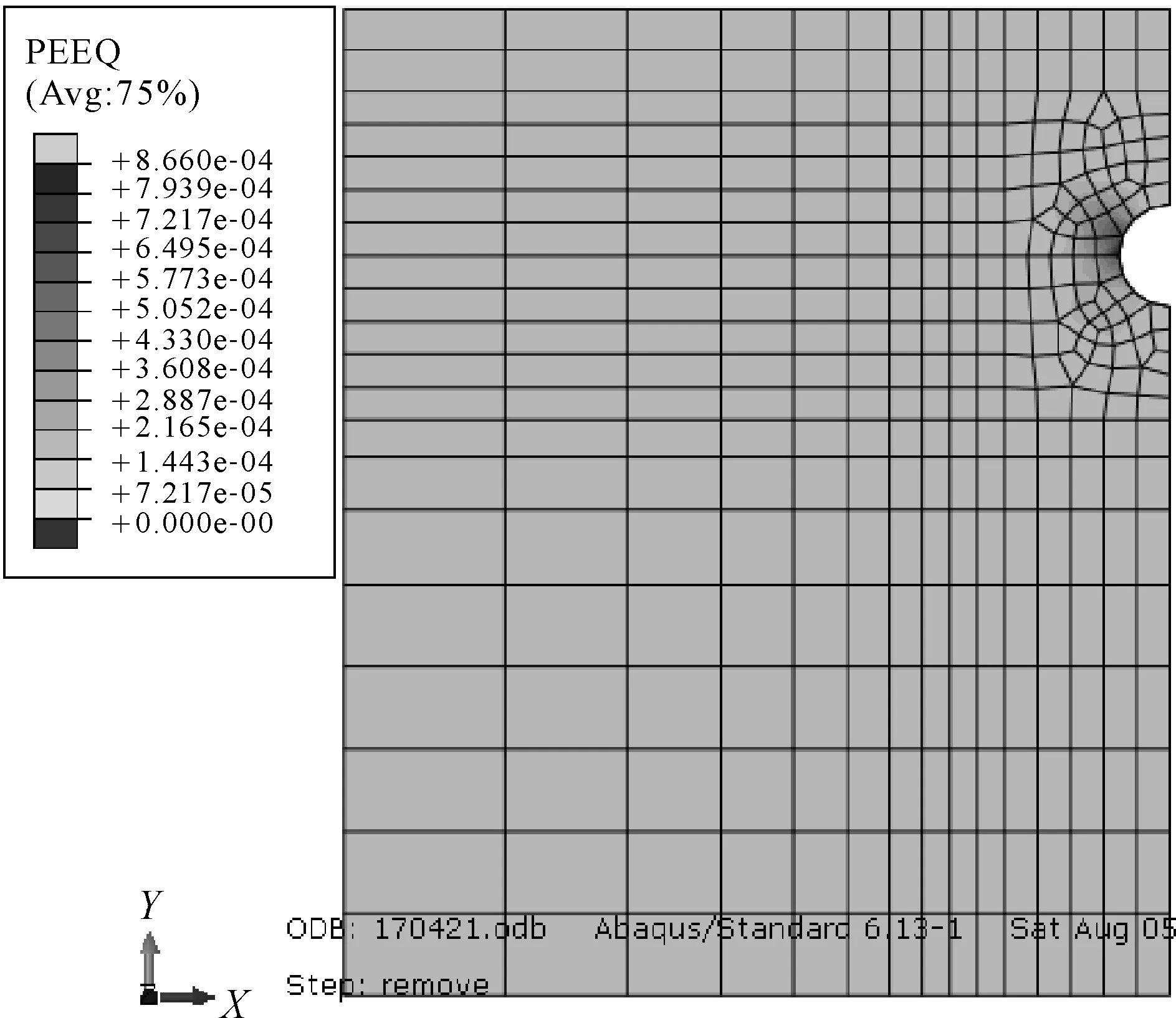
图2 施工完成时塑性应变分布

由于取对称模型,在后续分析时主要观察下述20个点位的沉降值(单位mm),见图3。以隧道中部点横向向左每隔1 m左右取10个观测点,绘制其在开挖过程中不同阶段的沉降变化,见图4。隧道开挖过程中前期由于土体挠动隧道部分会有向下3 mm左右的沉降,在衬砌安装完成以及土体挖空后会逐渐恢复并有部分反弹隆起,水平影响范围主要集中在2倍外径之内。

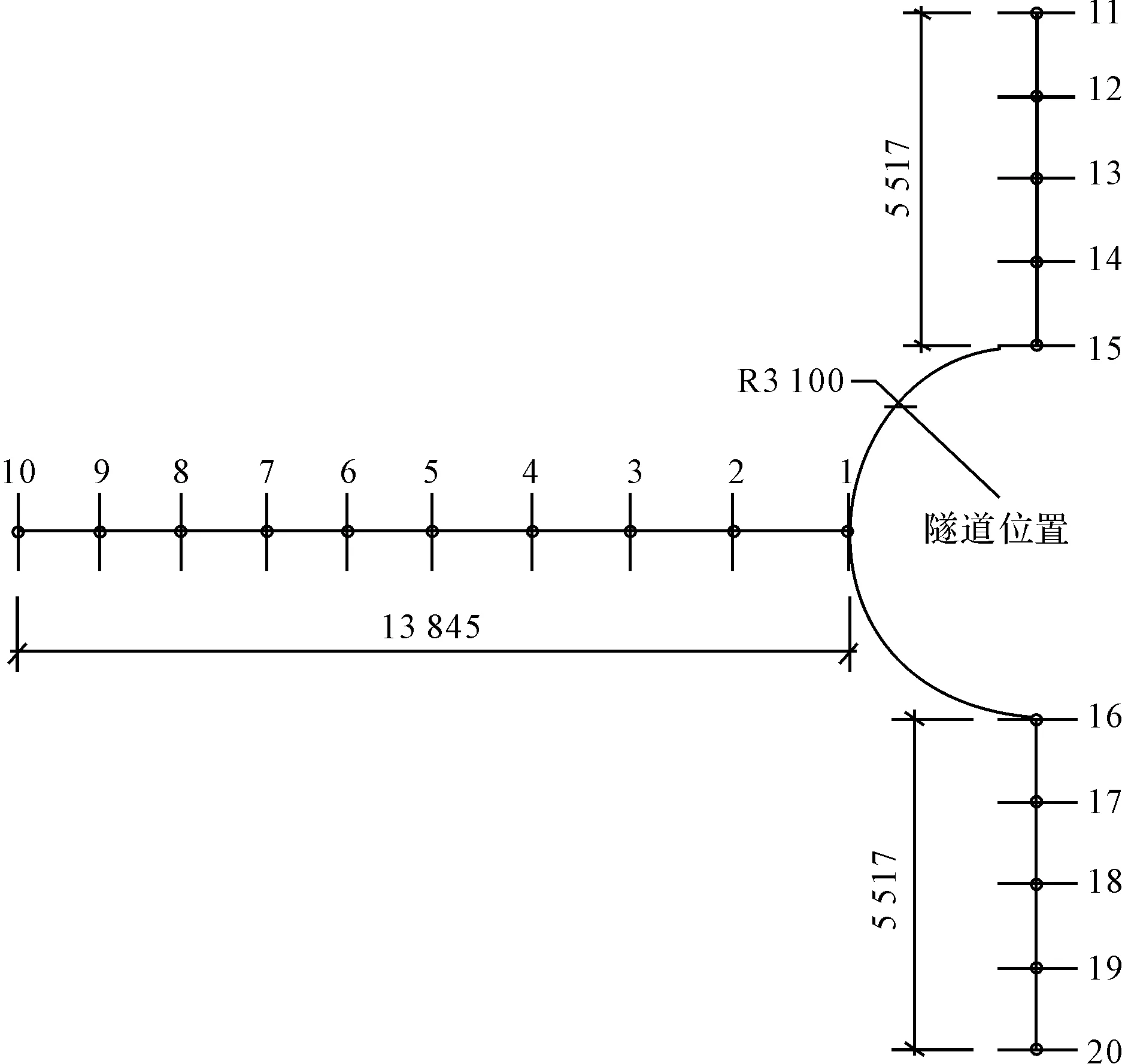
图3 沉降观察点位示意图

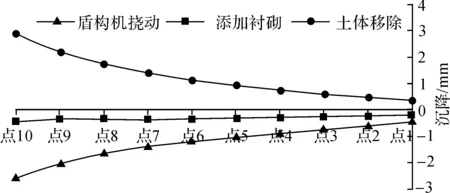
图4 不同施工步中各水平点位沉降对比图

同理,绘制隧道竖向各点位在施工不同阶段下的变形,见图5。隧道上下两部分都有一个先下沉再上升的过程,施工开始时,由于开挖挠动,隧道顶部会下沉约5 mm,底部变化不明显；而施工结束后,隧道底部会隆起约4 mm,顶部逐渐恢复初始状态。

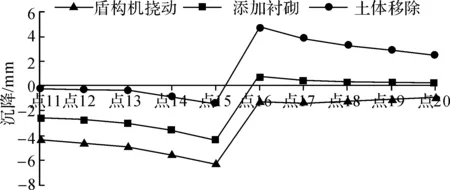
图5 不同施工步中各竖向点位沉降对比图

绘制隧道开挖过程中,隧道上部土体表面处沉降的实测数据与有限元数据对比见图6。有限元结果最大沉降约3.5 mm,略小于实测数据最大沉降约4.5 mm。有限元结果的沉降槽宽度约55 m,略大于实测数据约40 m。分别取隧道周边上、下、左侧各两点(对称模型, 右侧同左侧), 得出其排水固结沉降(主固结沉降)随时间变化曲线见图7。各点位在底部渗水工况下固结沉降量大致为40 mm左右,其中顶部13号点位沉降最大,达到53 mm；底部18号点位沉降最小,约30 mm。整个固结沉降历时9.32×106s,对应约107 d。

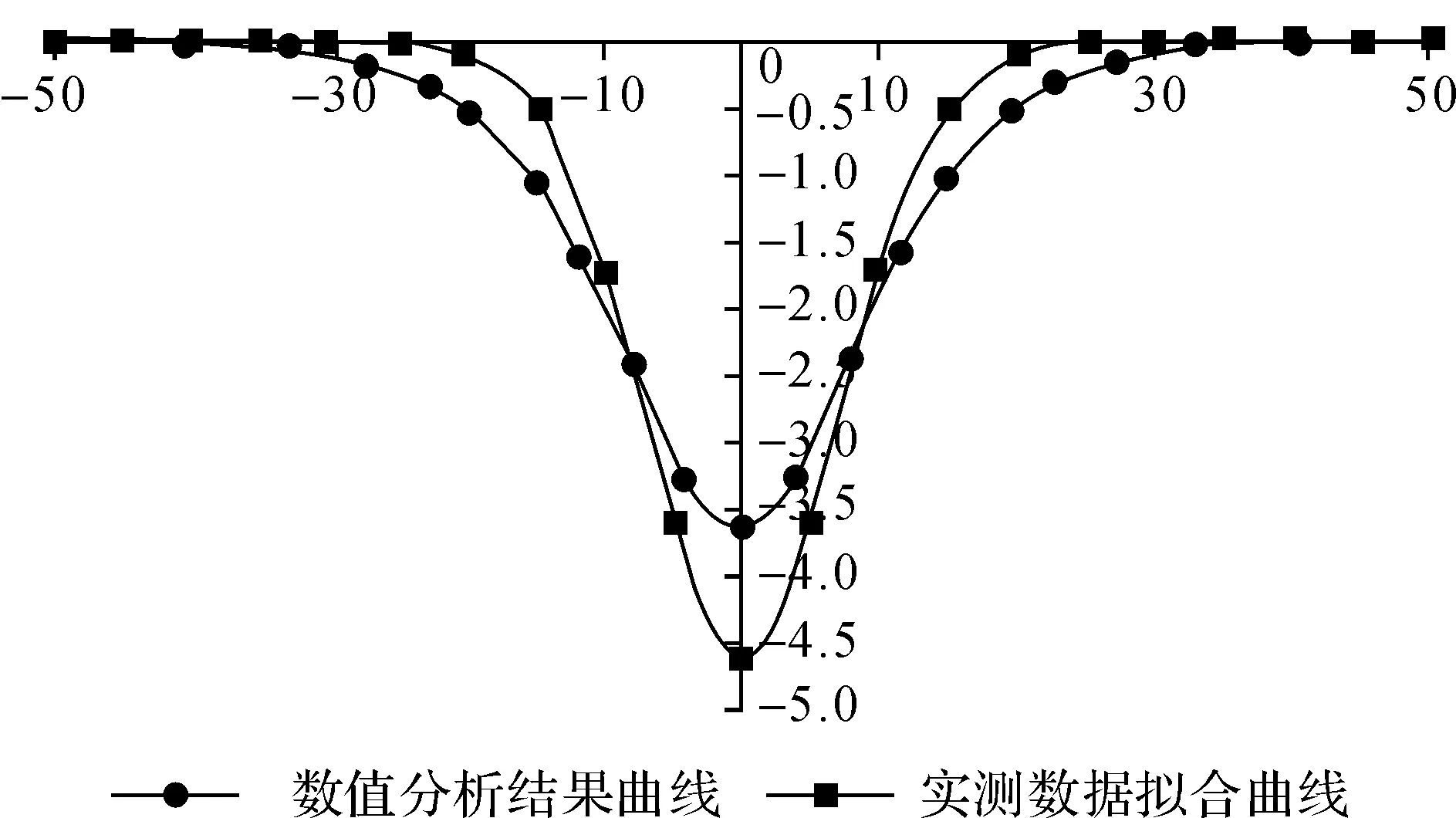
图6 开挖过程中地表处实测沉降与有限元结果对比图

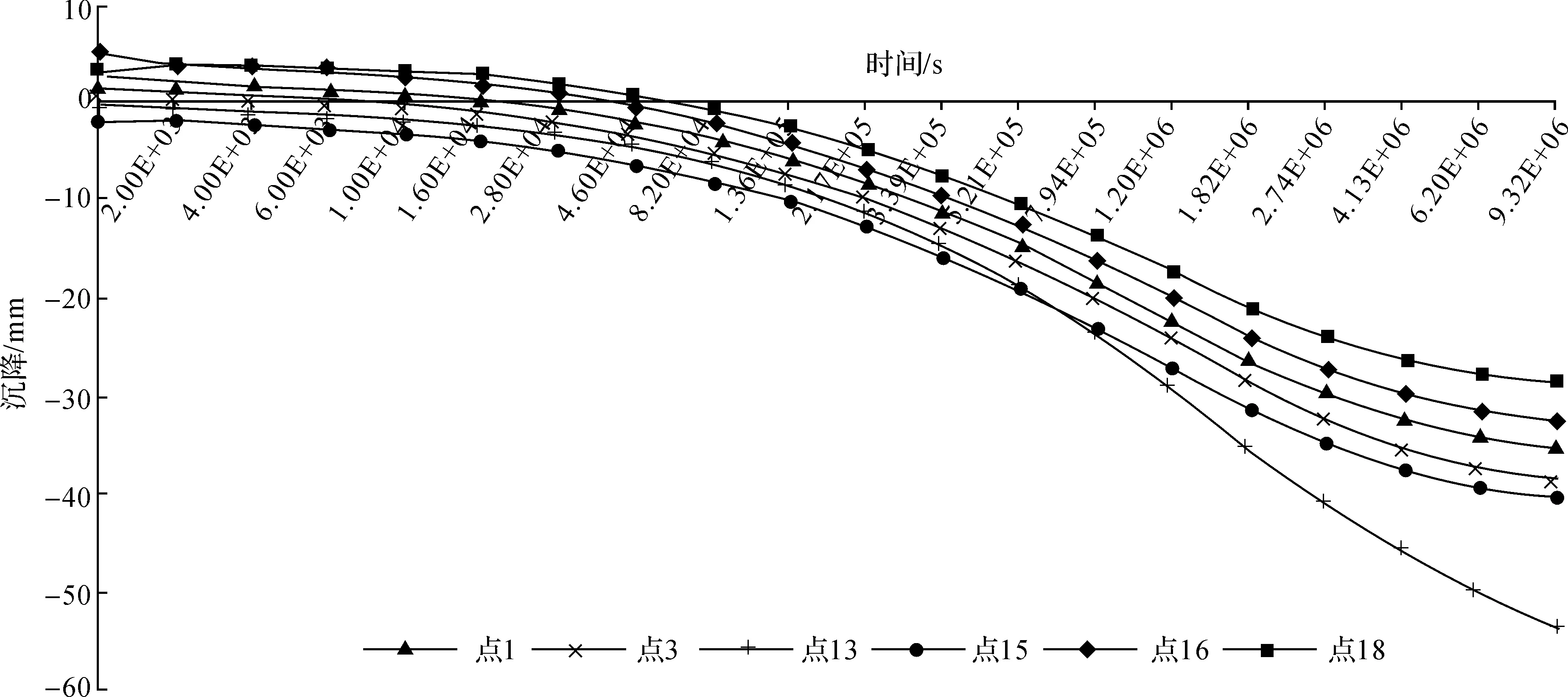
图7 不同位置土体静置期间固结引起的沉降

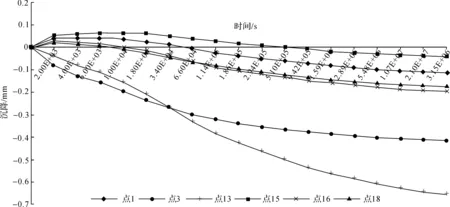
图8 不同位置土体静置期间蠕变引起的沉降

由于蠕变引起的沉降(次固结沉降)较小(远小于某些点位施工结束时的沉降), 在一张图上绘制各个点位的实际沉降曲线,各点的沉降不直观,因此绘制上述6个点位的蠕变引起的沉降的增量曲线,见图8。计算所得蠕变引起沉降不超过1 mm,可能是由于浅埋隧道导致的土体所受应力水平,尤其是偏应力水平较低。13号点位和3号点位蠕变引起沉降量明显高于其他点位,尤其隧道上部13号点位,其固结和蠕变沉降都高于其他部分。

4 结 语

1)软土地区浅埋隧道在开挖过程中,隧道两侧中部偏上的位置会产生较大塑性变形,进而引起隧道上部塌陷,底部隆起,隆起高度约5 mm。隧道上部地表处沉降极值约4 mm,沉降槽宽度约55 m,与实测数据基本吻合。

2)软土地区浅埋隧道在静置期间,主要发生排水固结(主固结)沉降及土体蠕变(次固结)沉降。在衬砌底部渗水工况下,排水固结沉降能达到40～60 mm,其中隧道上部区域受影响最严重。对于浅埋隧道,在应力水平相对较低的情况下,蠕变引起的沉降不明显。

参 考 文 献

[1] 王军,谷川,蔡袁强，等.动三轴试验中饱和软黏土的孔压特性及其对有效应力路径的影响[J].岩石力学与工程学报,2012,31(6):1290-1296.

[2] 侯芳.均布荷载作用下温克勒弹性地基梁解析解及其在盾构隧道纵向计算中的应用[D].青岛:青岛理工大学,2009.

[3] 徐冬健. 盾构隧道沉降数值模拟[D]. 北京：北京交通大学, 2009.

[4] 周念清, 唐益群, 娄荣祥,等. 徐家汇地铁站深基坑降水数值模拟与沉降控制[J]. 岩土工程学报, 2011, 33(12):1950-1956.

[5] 王金昌,陈页开. ABAQUS在土木工程中的应用[M]. 杭州：浙江大学出版社, 2006.

[6] 郭海柱, 张庆贺, 朱继文,等. 土体耦合蠕变模型在基坑数值模拟开挖中的应用[J]. 岩土力学, 2009, 30(3):688-692.

[7] 肖桃李, 邓雄. 塑性屈服准则在岩土工程中的应用分析[J]. 西部探矿工程, 2006, 18(8):1-4.

[8] 陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用[M].北京：中国水利水电出版社, 2010.