CT系统参数标定及成像建模
巢丽媛,邹娜,钟仁峰,刘财辉*
CT系统参数标定及成像建模
巢丽媛,邹娜,钟仁峰,刘财辉*
(赣南师范大学数学与计算机科学学院,江西赣州,341000)
本文主要基于 Radon 正反变换,建模研究 CT 系统参数标定以及成像原理。针对问题1,以正方形模板的中心点为直角坐标系的原点,水平方向为 X 轴,竖直方向为 Y 轴,运用几何方法、数据分析、图像拟合等方法,解出CT 系统探测器单元之间的距离为0.2768mm,其旋转中心的坐标为(-9.2734,5.9516)。CT系统的初始角度为33.0363°,终止角度为208.4130°,总共转过 175.3767°。针对问题二和三,以问题一中得到的角度信息作为 Radon 反变换的参数,绘制附件 2 的 CT 系统成像图。主要使用三次样条插值与像素坐标转化直角坐标等方法,解出成像图的吸收率和几何图的吸收率之间的关系为:
μ1=2μ2,转换得出几何图中各点吸收率值。
傅里叶函数;CFTOOL 工具箱;Radon 正反变换;三次样条插值
引言
CT(Computed Tomography)可以在不破坏样品的情况下,利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像,由此获取样品内部的结构信息。一种典型的二维 CT 系统如图 1 所示,平行入射的 X 射线垂直于 CT 系统器平面,每个 CT 系统器单元看成一个接收点,且等距排列。X 射线的发射器和 CT 系统器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转 180 次。对每一个 X 射线方向,在具有 512 个等距单元的 CT 系统器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到 180 组接收信息。
CT 系统安装时往往存在误差,从而影响成像质量,因此需要对安装好的 CT 系统进行参数标定,即借助于已知结构的样品(称为模板)标定 CT 系统的参数,并据此对未知结构的样品进行成像。
请建立相应的数学模型和算法,解决以下问题:
(1)在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图 2 所示,相应的数据文件见附件 1,模板每一点的数值反映了该点的吸收强度,这里称为“吸收率”。对应于该模板的接收信息见附件 2。请根据这一模板及其接收信息,确定 CT 系统旋转中心在正方形托盘中的位置、CT 系统器单元之间的距离以及该 CT 系统使用的 X 射线的 180 个方向。
(2)附件 3 是利用上述 CT 系统得到的某未知介质的接收信息。利用(1)中得到的标定参数,确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。另外,请具体给出图 3 所给的 10 个位置处的吸收率,相应的数据文件见附件 4。
(3)附件 5 是利用上述 CT 系统得到的另一个未知介质的接收信息。利用(1) 中得到的标定参数,给出该未知介质的相关信息。另外,请具体给出图 3 所给的10 个位置处的吸收率。
1 模型假设与符号约定
模型假设
(1)假设 X 射线能够全部覆盖被测物体;
(2)将一条 X 射线抽象为一个质点;
(3)假设每条 X 射线的入射强度不变。
(4)假设每个像素块的吸收率是相同的
(5)假设所给束足够可靠。
符号约定与说明
(5)I1入射强度
(6)μ物质得衰减系数
(7)μ1附件一的吸收率
(8)μ2附件二的吸收
2 问题一的分析与求解
2.1 问题的分析及数据处理
问题一需要我们通过附件 1 和附件 2 以及模板的图片等信息来标定一个 CT 系统的参数(包括旋转中心,CT 系统单元之间的距离,以及系统旋转的方向)。
分析附件二的图像和系统旋转的情况,可以得到系统旋转时两个特殊的方向
(水平方向和竖直方向),这两个特殊方向的信息加上两个物体的图形信息,可以得到系统的旋转中心和 CT 系统单元之间的距离。

两种情况下,X 射线通过模板之后,所吸收的能量最大(如下图所示):
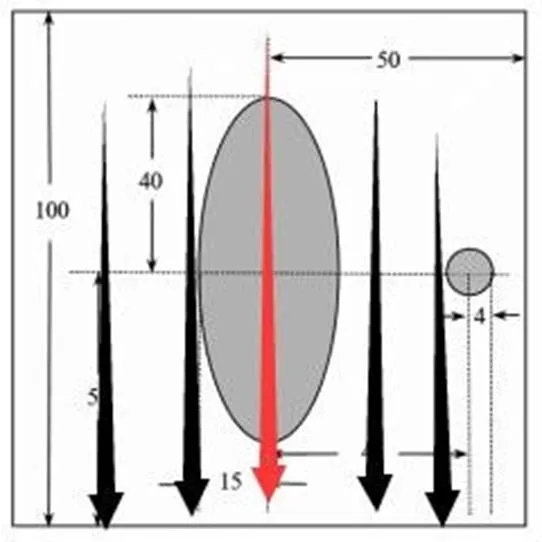
图1 其中一条 X 射线穿过椭圆长轴
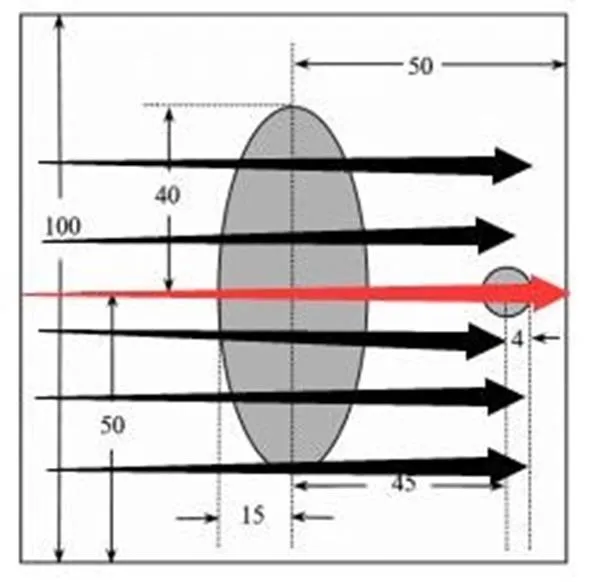
图2 其中一条 X 射线穿过椭圆短轴
图 1 是所有射线与水平方向成 90°的情况,此时,存在一条射线恰好通过 椭圆的长轴,在这个方向下,这条射线的 CT 系统单元返回的能量信息是所有射线中最大的。在附件二中筛选出这条射线的 CT 系统单元标号为 235,方向是第61 次旋转所得方向。
图 2 是所有射线与数值方向成 90°的情况,此时,存在一条射线恰好通过椭圆的短轴,在这个方向下,这条射线的 CT 系统单元返回的能量信息是所有射线中最大的,在附件二中筛选出这条射线的 CT 系统单元标号为 223,方向是第151 次旋转所得方向。
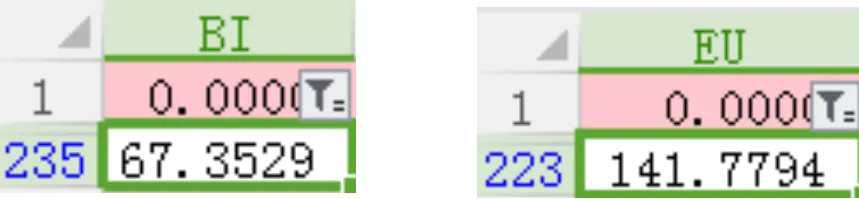
表1 从附件 2 中筛选得到的 CT 系统单元与方向信息
(列标为方向,行标为 CT 系统单元标号)
2.2 问题一的求解
2.2.1 CT 系统单元之间的距离
在图 3 的情况下,存在通过椭圆长轴的一簇射线束,这些射线束即为具有能量返回信息的射线束,可以在附件 2 中统计得到这一簇射线束中 X 射线的数量为289。X 射线的数量即为 CT 系统单元的数量 289。
通过题中给出的模板示意图,已知条件容易得到椭圆长轴的长度为 80mm。80mm对应 289 个 CT 系统单元的 288 段间距,而每段间距又是相等的,故使用d表示 CT 系统单元之间的距离,a 表示椭圆长轴,用如下公式计算。

求得 CT 系统单元之间的距离d = 0.2768 (单位:mm)。
2.2.2 旋转中心在正方形托盘中的位置
在整个 CT 系统中,旋转中心的位置一定处于 CT 系统单元 256 与 CT 系统单元 257 所发射出的两条 X 射线的中间。
为了确定旋转中心在正方形托盘中的位置,我们需要将 CT 系统与正方形托盘上的模板联系起来看,当 CT 系统旋转到 3.1 中图1 和图2 所示的两个位置时,分别有两个 CT 系统单元(235、223)发出的射线恰好经过椭圆或圆的中心。CT 系统单元 256、257 与这两个 CT 系统单元(235、223)的相对位置可以确定,在图像中心建立笛卡尔直角坐标系,就可以得到旋转中心的坐标。
计算吸收量最大的 CT 系统单元与 CT 系统单元 256 和 CT 系统单元 257 之间的间隔,间隔乘以相邻 CT 系统单元之间的距离,即可得到旋转中心距离 x 轴与y 轴的距离(假设 235 号射线与 223 号射线是 x 轴和 y 轴,椭圆的中心是原点 O)。

图3 旋转中心在图中的位置
旋转中心的坐标(-9.2734,5.9516)(单位:mm)
2.2.3 旋转180次的方向
二维图像重建算法常用傅里叶变换。设 f (x, y) 表示一个二维图像,其傅里叶变换为:
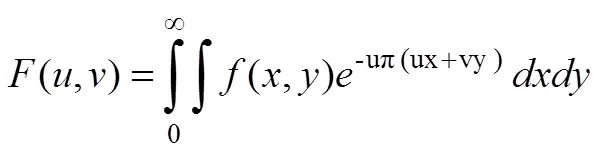
这个二维图像在与 x 轴夹 角的射线 s 上的投影的傅里叶变换,恰好等于这个二维图像 f (x, y) 的二维傅里叶变换[3]。
CT 系统旋转时,二维图像 x 轴夹θ角的射线 s 上的投影在变化,也就是傅里叶函数在变化,这些变化恰好能体现这 180 次旋转方向的变化,我们认为这种角度的变化满足傅里叶函数。在附件 2 中,随机选取几条 X 射线所吸收的能量值随 180 个方向的变化,使用 MATLAB 中 CFTOOL 工具箱拟合图像,如图4所示。
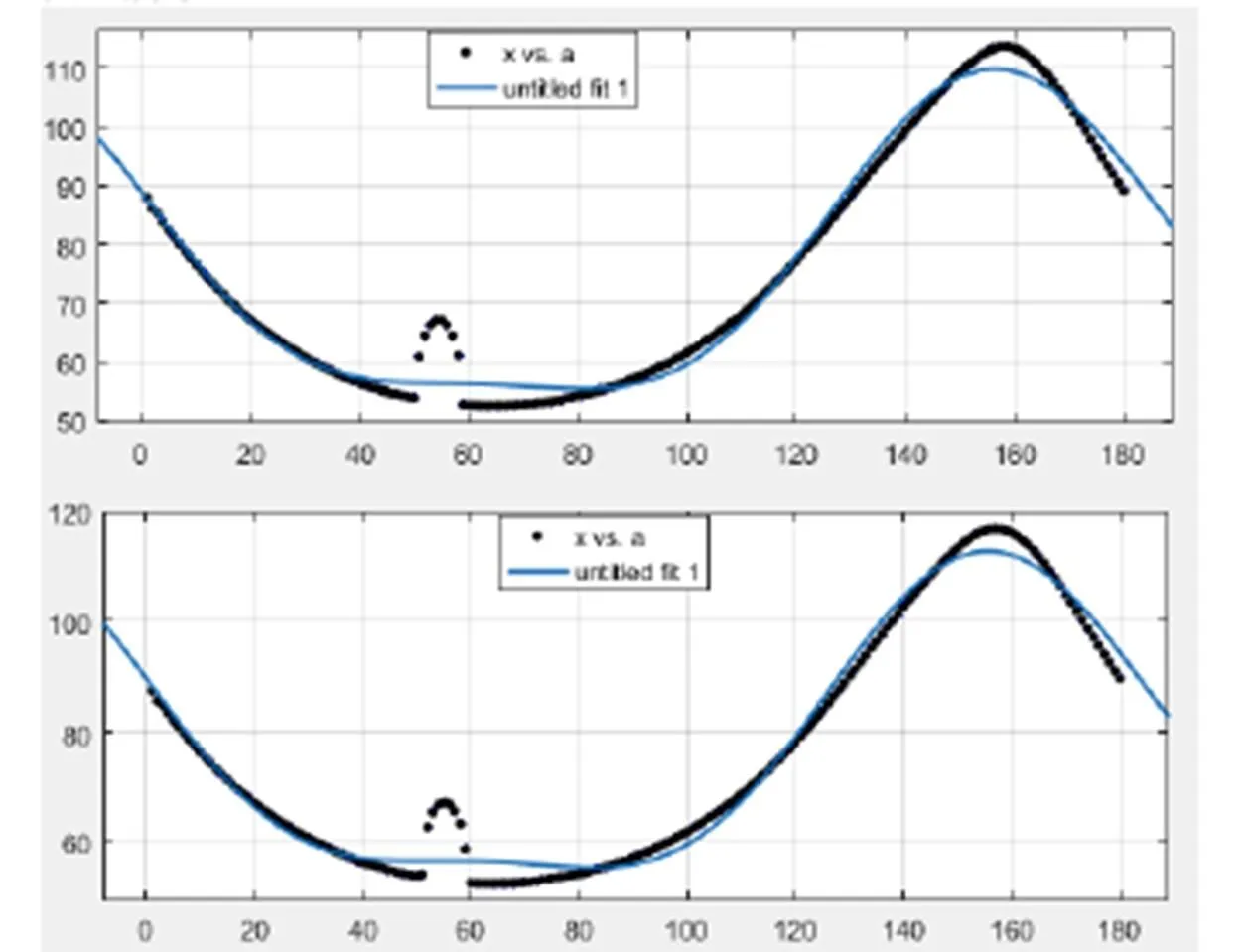
图4 随机选择的两条拟合图像
表2 两条曲线拟合的结果

(见附件拟合.xlsx)
上图和上表容易看出,拟合的精度很高。
将拟合所得的结果处理之后,得到角度变化所满足的傅里叶函数:
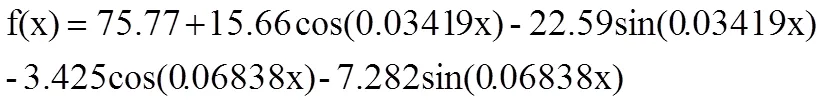
将得到的曲线的函数值(即对应附件 2 中的信息)带入上述函数,解得对应f(x)下x的值,即 180 个变化的θ值。
表3 180 个角度值

(见附件 theta.xlsx)
上述数据中,初始角度0 33.0363,终止角度t 208.4130,转过的角度175.3767.
3 问题二的模型建立与求解
3.1 问题二的数据分析
3.1.1 Radon 变换与反变换
定义函数 f (x, y) 在平面上沿直线 L 的线积分为:
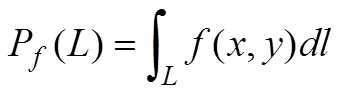
此线积分表达式即为 Radon 变换。
数学家 Radon 给出了上述公式 4.1 的逆变换表达式:
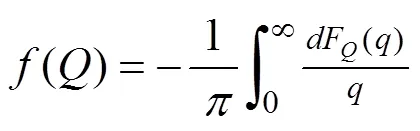
Q 是坐标轴上任意一点,q 是直线 L 到点 Q 的距离, FQ (q) 是关于 L 的线积分 Pf (L) 对所有 q 的平均值,公式 4.2 即为 Radon 反变换。
根据 Beer-Lamber 定律,X 射线的强度衰减满足:

当X 射线穿过不同衰减系数的材料组成的非均匀物体时,公式4.3 应该写成:
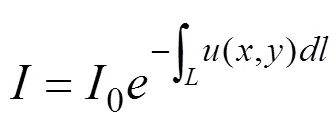
其中(,)是 (,) 沿 L 的线积分,化简公式 4.4,会得到一个类似于Radon 变换的形式:
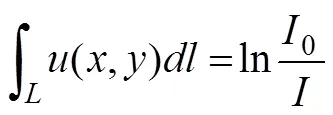
3.1.2 利用标定参数得到几何图
问题二需要我们求解附件 3 中未知介质在正方形托盘中的位置、几何形状和吸收率等信息。首先我们需要在 CT 系统成像图中得到原几何图的信息。通过问题 1 中标定得到的参数——180 个旋转角度以及附件 2 中的能量信息,使用 iradon 函数绘制出模板的 CT 系统成像图像。这一点容易用 MATLAB 实现。
通过问题 1 中标定得到的参数——旋转中心和 CT 系统单元之间的距离,在CT 系统成像图中选取出原几何图的信息。
根据计算,得到 CT 系统成像图的对角线宽是 512 个 CT 系统单元的总宽度,即 CT 系统单元数与 CT 系统单元之间距离的乘积。而且, CT 系统成像图的中心是 CT 系统的旋转中心。如此,可以标定 CT 系统成像图的实际坐标(单位: mm),通过实际坐标与原几何图标定坐标之间的关系确定原几何图的中心和几何图的边缘。
3.2 模型二的建立
3.2.1 建立几何图形
首先,将通过 radon 变换得到的像素为 362 的图像扩展为像素 512 的图像,此时图像的实际长度为 141.4447mm。
在 CT 系统图的中心选择坐标为(256.5, 256.5),即为旋转中心的坐标,对应原几何图中的实际坐标为(-9.2734, 5.9516)(单位: mm)。
利用问题一中 CT 系统器水平方向与竖直方向的 X 射线 223 和 235 与中心线之间的关系,几何图中心点在 CT 系统成像图上的坐标为(289, 277)。关于几何图的边缘计算,有如下等式:

解得 x=y=361,即白色边框的边长。
3.2.2 获取吸收率矩阵
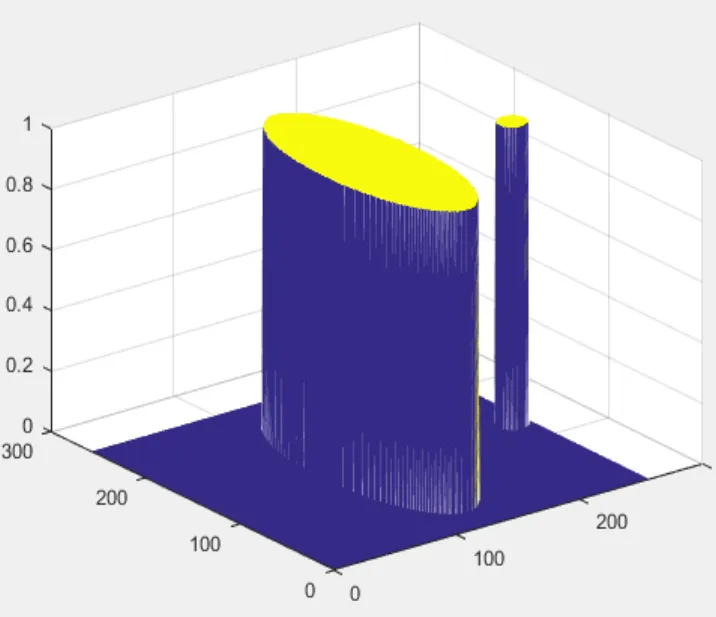
图6 几何图吸收率的三维图像

图7 CT系统图吸收率的三维图像通过
几何图吸收率三维图像与CT系统图吸收率三维图像的吸收率之间的关系得到:

由于在 CT 系统成像图中得到的几何图的像素图大小是 361*361 的矩阵,而几何图的本身像素大小是 256*256 的矩阵,为了实现成像图中几何图信息到实际几何图信息的转换,我们对 CT 系统图吸收率的三维图像进行插值处理,得到更详细的吸收率值。
使用插值后的成像图,根据几何图和成像图的边长比,将几何图的距离映射到插值后的成像图中,即求出 256*256 像素块在插值后的成像图中的坐标,根据几何图吸收率与成像图的上述关系,从而求出几何图中每个像素块的吸收率。
3.3 模型二在附件 3 的应用
3.3.1 附件 3 物体在正方形托盘中的位置,以及几何形状
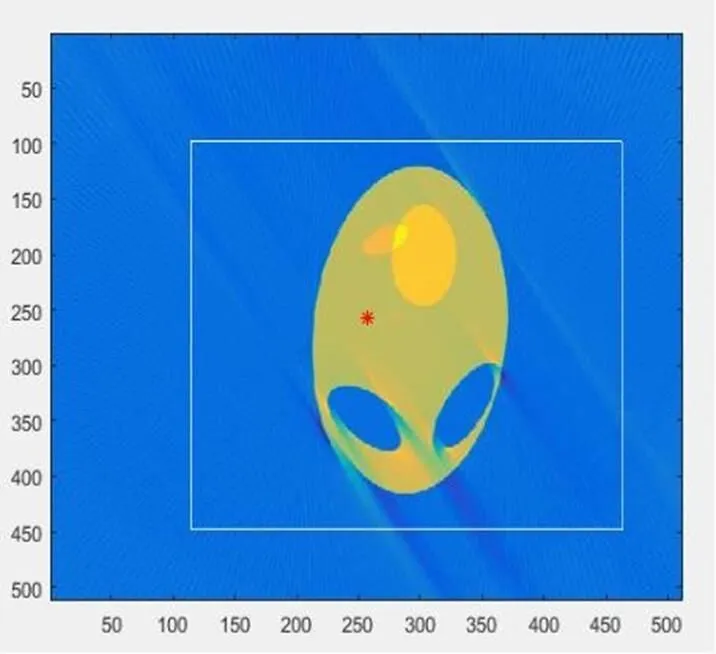
图8 附件 3 的物体信息
3.3.2 附件3物体的吸收矩阵
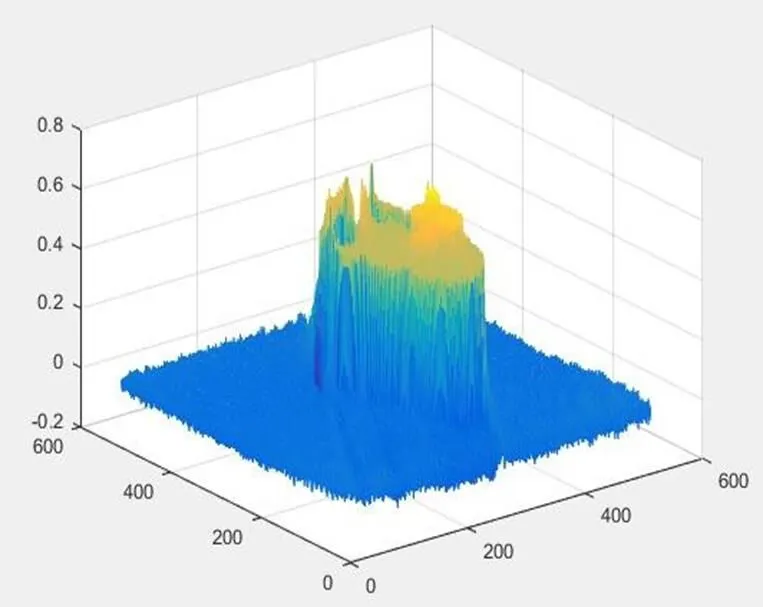
图 9 附件 3 的吸收率三维图像
吸收率矩阵见附件 problem2.xls

图10 通过吸收率矩阵重建的图像
十个点的坐标以及对应的吸收率:
表4 问题二对应的十个点的吸收率值

4 问题三的分析与求解
与模型二中的处理方法类似,首先得到 CT 系统成像图,在 CT 系统成像图中标定几何图的位置,如下图中白色方框框选的部分。
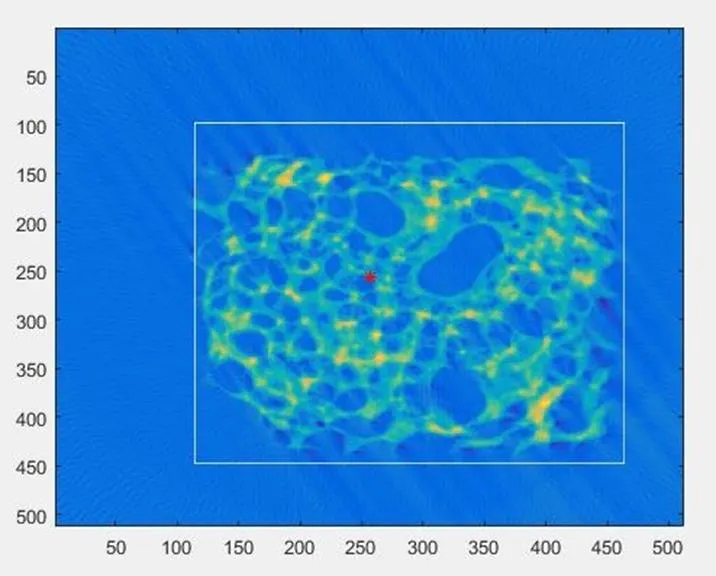
图11 附件 5 的物体信息
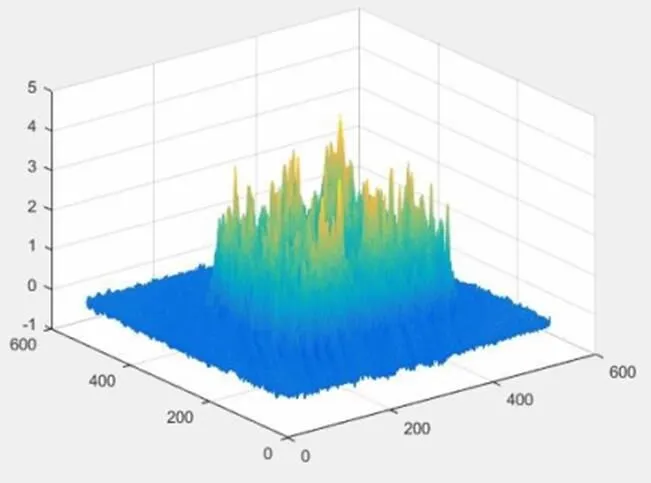
图12 附件 5 的吸收率的三维图像
吸收率矩阵见附件 problem3.xls

图13 通过吸收率矩阵重建的图像
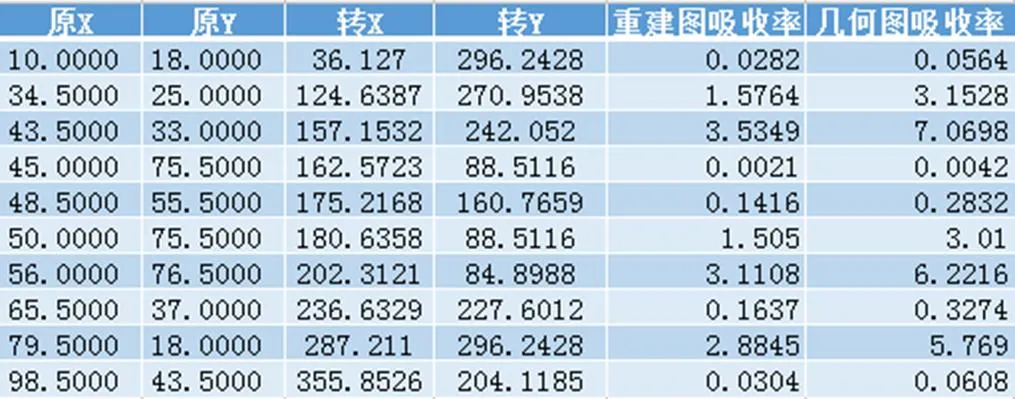
十个点的坐标及其对应的吸收率:
表5 问题三对应的十个点的吸收率
[1] 姜启源, 谢金星, 叶俊著. 数学模型(第四版)[M]. 高等教育出版社, 2011.
[2] 阮秋琦著. 数字图像处理学[M]. 电子工业出版社, 2013.
[3] 朱翚, 王富东. 利用 MATLAB 实现二维图像傅立叶变换算法[J]. 计算机应用与软件, 2006, (12): 141-142.
[4] 梁力, 尹东斐, 王川. 高精度摄像机标定模板的设计及识别算法[J/OL]. 西安交通大学学报, 2011, 45(04): 82-85.
[5] 李翰威. 锥形束CT系统几何伪影校正技术研究[D]. 南方医科大学, 2015.
[6] 陈健, 黄政仁, 刘学建, 等. CT系统放大倍数与极限空间.
[7] 姚明, 丛鹏, 刘锡明. 平板探测器CT系统调校及参数获取方法[J]. 原子能科学技术, 2013, 47(06): 1019-1022.
[8] 刘兴龙, 孙宏, 李琛玮, 等. CT能量成像技术原理和应用[J]. 中国医疗设备, 2012, 27(09): 1-7+45.
[9] 刘文艳, 许友军, 刘亚春. MATLAB在傅里叶变换课堂教学中的应用[J]. 湘南学院学报, 2015, 36(02): 71-74.
[10] 康家方, 王红星, 钟佩琳, 等. 基于傅里叶变换的非正弦时域正交调制系统实现方法[J]. 上海交通大学学报, 2014, 48(10): 1415-1420.
[11] 毕清华. Radon变换奇性检测与反演的研究[D]. 北京交通大学, 2007.
[12] 廖永忠, 蔡自兴, 何湘华. 一种基于局部Radon变换运动模糊图像参数估计算法[J]. 小型微型计算机系统, 2014, 35(01): 133-136.
[13] 王丽新. 双能CT基物质分解算法应用研究[D]. 山东大学, 2016.
[14] 桂叶晨. 基于CUDA的锥束CT重建与CT图像可视化技术研究[D]. 南方医科大学, 2009.
[15] CT成像: 基本原理、伪影与误区[J]. 中国介入影像与治疗学, 2015, 12(08): 492.
Parameter Calibration and Mmodeling of CT System
CHAO Liyuan, ZOU Na, ZHONG Renfeng, LIU Caihui*
(School of mathematics and computer science, Gannan Normal University, Jiangxi Ganzhou, 341000, China)
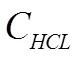
Fourier Transform; CFTOOL; Radon Transform; Cubic Spline Interpolation
10.19551/j.cnki.issn1672-9129.2018.01.012
TP39
A
1672-9129(2018)01-0027-05
巢丽媛, 邹娜, 钟仁峰, 等. CT系统参数标定及成像建模[J]. 数码设计, 2018, 7(1): 27-31.
CHAO Liyuan, ZOU Na, ZHONG Renfeng, et al. Parameter Calibration and Mmodeling of CT System[J]. Peak Data Science, 2018, 7(1): 27-31.
2017-10-21;
2017-12-13。
国家自然科学基金(61305052),赣南师范大学校级教改课题(150656)。
巣丽媛(1997-),女,赣南师范大学数计学院15 软本2 班本科生;
刘财辉(1979-),男,副教授,博士,硕士生导师,研究方向:数据智能处理与应用、机器学习等。E-mail:839783509@qq.com

