ANALYTIC APPROACH TO SPHERICALLY CONVEX SETS IN Sn−1

SHAO Yu-cheng,GUO Qi

(Department of Mathematics,Suzhou University of Science and Technology,Suzhou 215009,China)

1 Introduction

In light of the signi ficance and the successful applications of the convexity of sets(in linear spaces)in many different mathematics branches,it is not unexpected for mathematicians to try to find its counterpart for sets in manifolds.Such an attempt started from the early 1940’s with sets in Sn−1,the unit sphere in the Euclidean space Rn,since it is a typical manifold(see[2,6,9–11,13]and the references therein).

Several different de finitions of convex sets in Sn−1were proposed since 1940’s.For instance,a set in Sn−1is called strongly convex if it contains no antipodal points(x1,x2∈Sn−1are called(a pair of)antipodal points if x2= −x1)and it contains,with each pair of its points,the shorter arc of the great circle determined by them(see[2]);weakly convex if it contains,with each pair of its points,the shorter arc or a semicircular arc of a great circle determined by them(see[10]);Robinson-convex if it contains,with each pair of its non-antipodal points,the shorter arc of the great circle determined by them(see[6]);Hornconvex if it contains,with each pair of its non-antipodal points,at least one of the great circle arcs determined by them(see[6]).

Clearly,every strongly convex set is weakly convex and the weak convexity implies the Robinson-convexity,and the Robinson-convexity implies the Horn-convexity(see[2]).Also,simple examples show that all the inclusion relations here are proper.

Although various convexities for sets in Sn−1were proposed for different purposes and a great progress in the research was made in the early stage(see[2,6,9,10,13])and recently this topic regains the attentions of mathematicians(see[1,3,4,7,8]and the references therein),the progress in this area(in particular in the aspect of geometric invariants)seems not as fast as expected.One of the main obstacles of progressing is that all these de finitions of convexity for sets in Sn−1are in geometric forms,which made it complicated and even impossible to formulate or demonstrate some conclusions in the high dimension cases.This situation can be seen from several recent important work:Lassak in 2015 de fined the width of a strongly(or spherically)convex body(see below for de finition)and studied its elementary properties(see[7]),and further investigated the properties of(spherically)reduced bodies on spheres(see[8]),but the arguments he presented were somehow complicated due to his pure geometric methods.Similarly,Vigodsky’s early work on demonstrating an analogue of Carath´eodory’s theorem for strongly convex sets in S2(see[13])was also done by a geometric approach and thus hard to extend to the high dimension cases.Also,some authors have to deal with sets in Sn−1in the frame of Euclidean spaces(see[14]).

In this paper,taking strong convexity as an example,we present a pure analytic approach to de fining the convexity for sets in Sn−1and studying the basic properties of strongly convex sets in Sn−1.As an illustration,at the end we prove a structure theorem of Minkowski type for strongly convex sets in Sn−1.

2 Notation and De finitions

We work in the n-dimensional Euclidean space Rnwith the classical inner product〈·,·〉and the induced norm ‖ ·‖.For any non-zero u ∈ Rn,Hudenotes the hyperplane{x∈Rn|〈u,x〉=0},H−u(or H−simply)denotes the open half space{x∈Rn|〈u,x〉＜0},and(orsimply)denotes the closed half space{x∈Rn|〈u,x〉≤0}.

For non-empty C⊂Rn,co(C)and cone(C)denote the convex hull,the convex conical hull of C,respectively.For other notation and terms refer to[5].

A subset of the form H−∩Sn−1(resp.∩Sn−1)is call an open(resp.a closed)semi-sphere and a set of the form H ∩Sn−1is called a hypercircle.Generally,if Hk⊂ Rnis a k-dimensional subspace(1≤ k≤ n−1),then Hk∩Sn−1is called a k-circle.Thus a hypercircle is an(n−1)-circle and a 2-circle is a great circle named by other authors.

The main tool we used in our analytic approach is the radial function

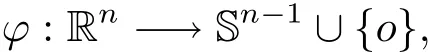
where o stands for the origin of Rn,de fined by

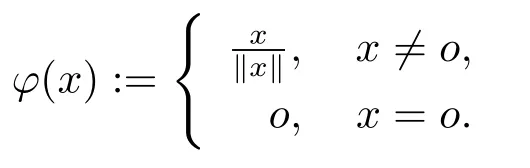
Observe that the radial function has the following properties

(1)ϕ◦ϕ=ϕ;

(2)ϕ(λx)= ϕ(x)for all x ∈ Rnand all λ ＞ 0;

(3) ϕ(x)=x iff x ∈ Sn−1or x=o.

In terms of the radial function,we have the following de finition.

De finition 2.1For x,y∈Sn−1and 0≤λ≤1,we de fine

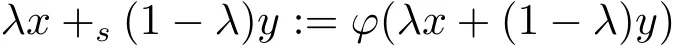
called a spherically convex combination of x,y(s-convex combination for brevity).

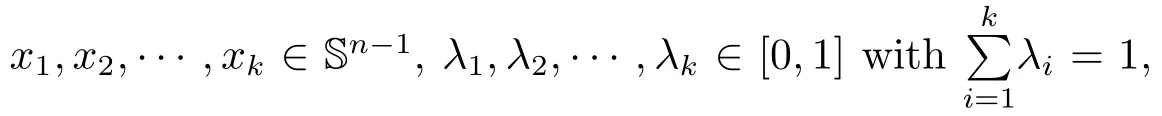
Natrually,when k=2,we write λx+s(1− λ)y instead of(s)(λx+(1− λ)y).

Remark 2.1i)x,y ∈ Sn−1are non-antipodal points iff λx+s(1−λ)yo or equivalently λx+(1−λ)yo for any 0≤λ≤1.

ii)In terms of De finition 2.1,the short arc of the great circle determined by nonantipodal points x,y∈ Sn−1is{λx+s(1− λ)y|0≤ λ ≤ 1}.

Now,we give the de finition of strongly convex sets in Sn−1in an analytic form,and we adopt“spherically convex”instead of“strongly convex”.

De finition 2.2A set C ⊂ Sn−1is called spherically convex(s-convex for brevity)if λx+s(1−λ)y∈C for any x,y∈C and 0≤λ≤1.

Remark 2.2i)By Remark 2.1,an s-convex set contains no antipodal points for sure,and C ⊂ Sn−1is s-convex iff it contains,with each pair of its points,the short arc of the great circle determined by them.

ii)It is easy to check that an open semi-sphere is s-convex while a closed semi-sphere,a k-circle and Sn−1are not since they all contain antipodal points.

The following simple property of s-convex sets will be needed later.

Proposition 2.1Let C ⊂ Sn−1be an s-convex set.Then we have

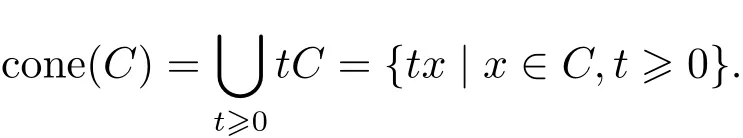
Moreover,cone(C)is closed iffC is closed(so compact).

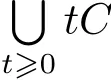
where we used the fact thatand so

The argument for the second conclusion is standard and straightforward.

3 Properties of s-Convex Sets and s-Convex Hull of Sets

In this section,we study basic properties of s-convex sets and in turn de fine the spherically convex hull(s-convex hull for brevity)of a set in Sn−1.We start with the following simple property.

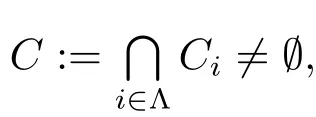
ii)If C is s-convex and Sk:=Hk∩Sn−1is a k-circle(2≤ k≤ n−1),then C∩Skis s-convex provided that the intersection is not empty.

Proofi)For any x,y∈C,we have x,y∈Cifor each i∈Λ.So x+sy∈Cifor each i∈Λ by the s-convexity of Ciand in turn x+sy∈C.

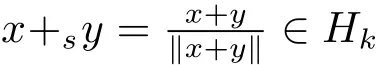
Next is an analogue of the conclusion for convex sets in Rn,which is not easy to formulate and prove in a geometric approach.

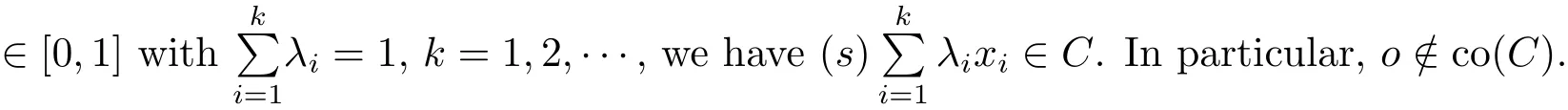
ProofIt is trivial for k=1,2 by De finition 2.2.Suppose the conclusion holds for all 1≤j≤k−1(which implies,in particular,that oco{x1,x2,···,xj}for anyNow for x1,x2,···,xk∈ C and(we may clearly assume λi＞ 0 for all i),we denoteClearly,zo and∈ C by the induction hypothesis.

Thus we have,by De finition 2.1 and the properties of ϕ,

where we used the fact that∈ C and

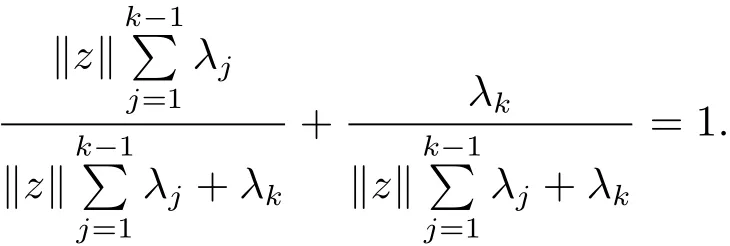
Now,oco(C)is trivial.

Next,we consider the spherically convex hull of a set in Sn−1,i.e.,the smallest s-convex set containing a set.Since if C⊂Sn−1is s-convex,then oco(C)by the de finition and in turn o/∈co(S)if S⊂C,so we see that a set S⊂Sn−1has a spherically convex hull iffo/∈co(S).

De finition 3.1Given S⊂Sn−1with o/∈co(S),we de fine its spherically convex hull Sco(S)(s-convex hull for brevity)by

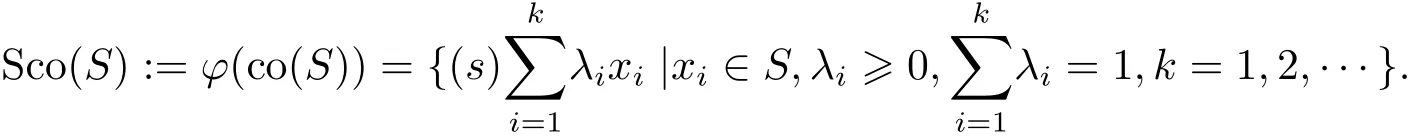
Theorem3.2Let S⊂Sn−1with o/∈co(S).Then

i)Sco(S)is s-convex.

ii)Sco(S)= ∩{C ⊂ Sn−1|C ⊃ S and C is s-convex},i.e.,Sco(S)is the smallest s-convex set containing S.

iii)Sco(S)=cone(S)∩ Sn−1.

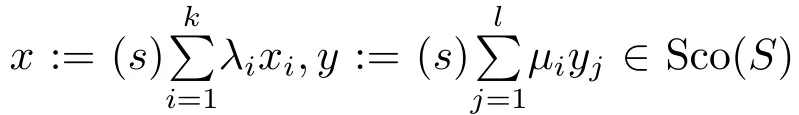
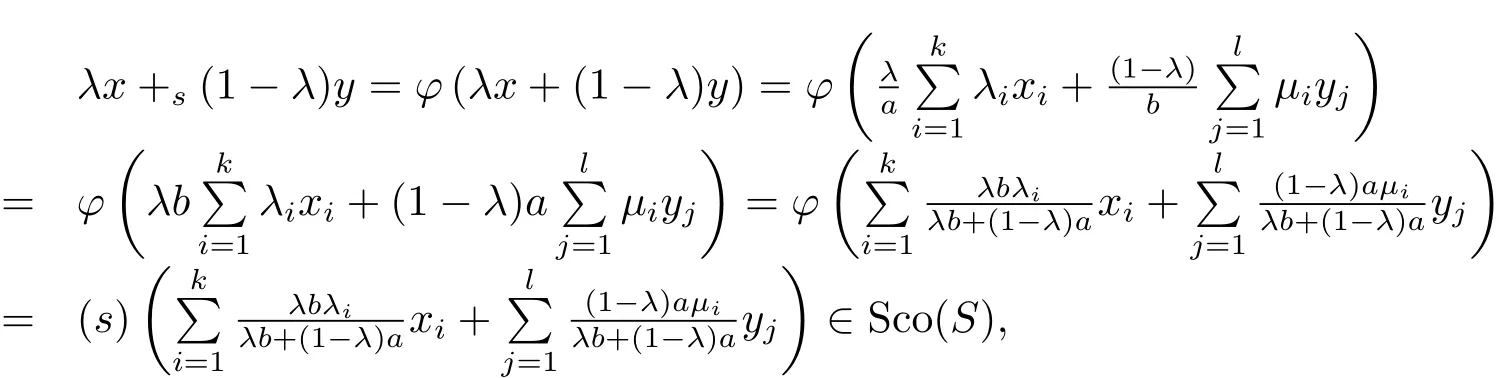
where we used the de finition of Sco(S)and the fact that

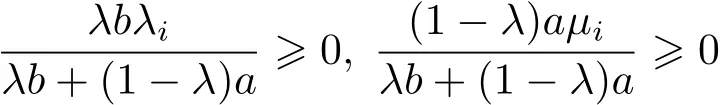
and

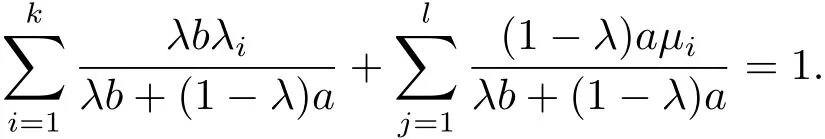
ii)Denote D:= ∩{C ⊂ Sn−1|C ⊃ S and C is s-convex}(D is well-de fined since Sco(S)⊃S and Sco(S)is s-convex by i)).Then D⊂Sco(S)clearly since Sco(S)⊃S and it is s-convex by i)above.Conversely,since for each s-convex C⊃S,Sco(S)⊂C by Theorem 3.1,we have Sco(S)⊂D.Therefore Sco(S)=D.

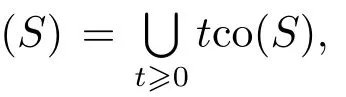
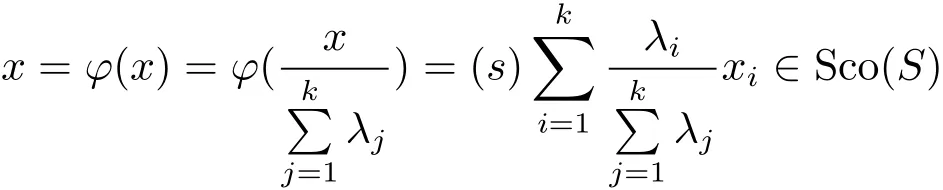
by the de finition of Sco(S)again.Hence cone(S)∩Sn−1⊂ Sco(S)and so Sco(S)=cone(S)∩Sn−1.

4 A Structure Theorem of Minkowski’s Type for Closed s-Convex Sets

In this section,we establish a theorem of Minkowski type for s-convex sets,which states that a closed s-convex set can be expressed as the s-convex hull of its s-extreme points(see below for de finition).We start with some necessary notation and terms.

For an s-convex C ⊂ Sn−1,we denote dimC=dim(cone(C))− 1(notice that cone(C)is convex),called the dimension of C,rbd(C):=rbd(cone(C))∩clC,where“rbd”in the right-handed side denotes the relative boundary,called the relative boundary of C and ri(C):=ri(cone(C))∩C=ri(coneC)∩Sn−1(the latter equality can be checked by Proposition 2.1),where “ri”in the right-handed side denotes the relative interior,called the relative interior of C.It is easy to show that if C ⊂ Sn−1is s-convex,then so is ri(C)and that if C is closed and s-convex,then C=rbd(C)∪ri(C).

De finition 4.1Let C ⊂ Sn−1be a closed s-convex set.A point x∈ C is called an s-extreme point of C iffor some x1,x2∈C,then x1=x2.The set of s-extreme points of C is denoted by Sext(C).

Remark 4.1It is easy to check that if x is an s-extreme point of C,then x∈rbd(C).

Proposition 4.1If C ⊂ Sn−1is a closed and s-convex set,then Sext(C)Ø.

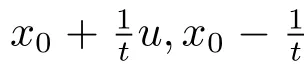
Thus,by the closedness of cone(C),we have

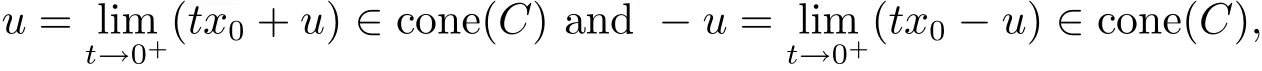
which together with ‖u‖ = ‖ − u‖ =1 leads to(the antipodal points)u,−u ∈ C by Proposition 2.1,a contradiction.

Since cone(C)is closed and line-free,it has at least one extreme ray by Theorem 1.4.3 in[12].Let L be an extreme ray of cone(C)and let x=L∩C.Then L={tx|t≥0}.Now,ifSo x1,x2∈L since L is an extreme ray and in turn x1,x2∈L∩C which leads to x1=x2=x clearly.Thus,x is an s-extreme point.

The following is a theorem of Minkowski type for closed s-convex sets in Sn−1,which,again,it is hard to prove in geometric methods.

Theorem 4.1Let C ⊂ Sn−1be a closed and s-convex set.Then C=Sco(Sext(C)).

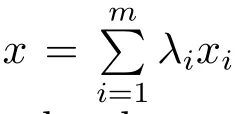
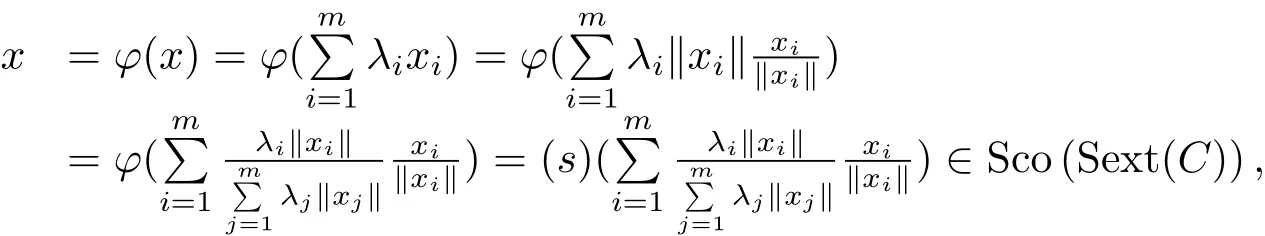
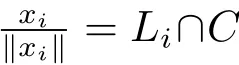
Final RemarkFrom Theorem 3.1 and Theorem 4.1,one can see that our analytic approach indeed makes it possible to formulate and demonstrate some conclusions which can hardly be formulated and proved by pure geometric methods.It is expectable that,with this analytic approach,more conclusions will be established and more concepts,such as the meaningful geometric invariants for s-convex sets etc.,will be proposed later.We leave these topics to other papers.

References

[1]Brummelen G V.Heavenly mathematics,the forgotten art of spherical trigonometry[M].Priceton:Priceton Univ.Press,2013.

[2]Danzer L,Grünbaum B,Klee V.Helly’s theorem and its relatives[J].Conv.Proc.Symp.Pure Math.,1963,7:99–180.

[3]Ferreira O P,Iusem A N,N´emeth S Z.Projections on to convex sets on the sphere[J].Glob.Optim.,2013,57:663–676.

[4]Gao F,Hug D,Schneider R.Intrisic volumes and polar sets in spherical spaces[J].Homage Luis Santal´o Vol.I,Math.Not.,2001,41(2):159–176.

[5]Hiriart-Urruty J-B,Lemar´echal C.Fundamentals of convex analysis[M].Berlin,Heidelberg,New York:Springer-Verlag,2001.

[6]Horn A.Some generalizations of Helly’s theorem on convex sets[J].Bull.Amer.Math.Soc.,1949,55:923–929.

[7]Lassak M.Width of spherical convex bodies[J].Aequ.Math.,2015,89:555–567.

[8]Lassak M.Reduced spherical polygons[J].Coll.Math.,2015,138(2):205–216.

[9]Robinson C V.Spherical theorems of Helly type and congruence indices of spherical caps[J].Amer.J.Math.,1942,64(1):260–272.

[10]Santal L´O.Propiedades de las figuras convexas s´obre la esfera[J].Math.Not.,1944,4:11–40.

[11]Santal L´O.Convex regions on the n-dimensional spherical surface[J].Ann.Math,1946,47:448–459.

[12]Schneider R.Convex Bodies:the Brunn-Minkowski theory(2nd ed.)[M].Cambridge:Cambridge University Press,2014.

[13]Vigodsky M.Sur les courbes ferm´ees`a indicatrice des tangentes donn´ee[J].Rec.Math.[Mat.Sbornik]N.S.,1945:73–80.

[14]Yang S G.Two classes of geometric inequalities of finite point set in space with constant curvature[J].J.Math.,2006,26(6):665–668.