DISTRIBUTIVE LATTICES WITH A HOMOMORPHIC OPERATION

LUO Cong-wen,WANG Gao-xia

(College of Science,China Three Gorges University,Yichang 443002,China)

1 Introduction

An algebra L is said to be subdirectly irreducible(s.i)if it has a smallest non-trivial congruence;i.e.,a congruence α,such that θ ≥ α for all θ ∈ ConL with θω.A particularly important case of a subdirectly irreducible algebra is a simple algebra,namely,one for which the lattice of congruence is the two-element chain{ω,ι}.Associated with the notion of a subdirectly irreducible algebra is that of a finitely subdirectly irreducible(f.s.i)algebra,this being de fined as an algebra in which the intersection of two non-trivial principal congruences is non-trivial.Clearly,every s.i.algebra is f.s.i.algebra and f.s.i.semilattices,distributive lattices and Boolean algebras are s.i.Many algebras arising in logic have(distributive)lattice reducts and share the same property;for example,De Morgan algebras[1],the Post algebras of order n,the n-valued Lukasiewicz algebras[2]and demi-p-lattices[3].In this paper,we consider the class of bounded distributive lattices endowed with an unary operation,which is an endomorphism f with f(0)=0,f(1)=1(the class will be denoted by eD),characterise finitely subdirectly irreducible algebras and the subdirectly irreducible algebras in eD.

2 Preminaries

Let(L,f)∈ eD and let f0=id and de fine fnrecursively by fn(x)=f(fn−1(x))for n≥1,then for p,q∈N with p＞q≥0,we de fine the subclass ep,qD of eD by adjoining the equation fp=fq.It follows that the smallest nontrivial subclass ep,qD is the class e1,0D,which is determined by the equation f=id.We de fine e2,0D to be the class of symmetric extended distributive lattices,see[4].

A congruence on L is an equivalence relation that has the substitution property for both the lattice operations and for the unary operation f.It follows that every congruence is in particular a lattice congruence and it is essential to distinguish these two types.In order to do so,we shall use the subscript ‘lat’to denote a lattice congruence.

Lemma 2.1(see[5])Let(L,f)∈eD.If a,b∈L with a≤b in L,then

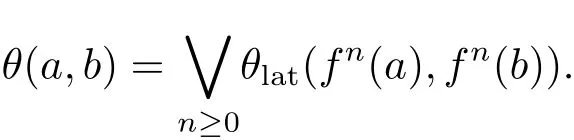
Corollary 2.1Let(L,f)∈e2,0D.Then

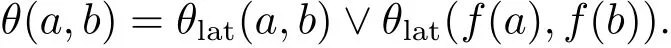
For an algebra(L;f)∈ eD,consider now,for every n ∈ N,the relation Φnon L de fined by

It is clear that Φnis a congruence on L.Moveover,the subset fn(L)={fn(x)|x ∈ L}is a subalgebra of L.

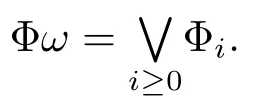
For every non-trivial algebra(L;f)∈eD,it is clear that we have

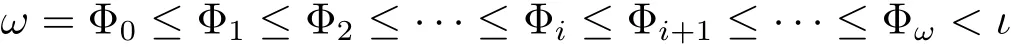
and with ≤ meaning“is a subalgebra of”,

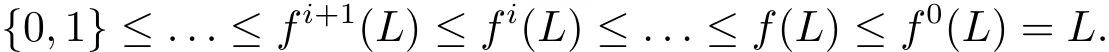
It is readily seen that[x]Φi→ fi(x)describes an algebra isomorphism in eD.We shall denote by writing

The following result is therefore clear.

Lemma 2.2If(L;f)∈ep,qD,then,for n≤q,

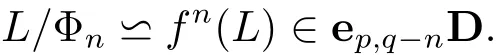
The following two lemmas are an extension to eD-algebras of Blyth for Ockham algebras[6].

Lemma 2.3If(L;f)∈ep,qD,then

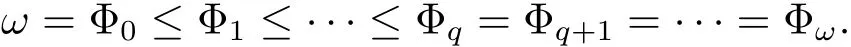
Moreover,if(L;f)belongs to the subclass ep,qD,then each of the above is equivalent to(L;f)∈ ep−q,0D.

Lemma 2.4If(L;f)∈ep,qD,a,b∈L are such that a≺b and f(a)=f(b)then θ(a,b)is an atom of ConL.

3 Subdirectly Irreducible Algebras

Given an algebra(L;f)∈eD,consider now for each i≥1 the subset

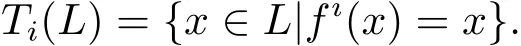
In particular,T1(L)is the set of fixed points of f.Of course,T1(L)is never empty,for it clearly contains 0 and 1.It is readily seen that every subset Tn(L)is a subalgebra of L;in fact Tn(L)is the largest en,0D-subalgebra of L.

Consider now the subset

T(L)={x∈L|there exists a positive integer mxsuch that fmx(x)=x}.

Given x,y∈T(L),let m=lcm{mx,my}.Then,m being positive integer,we have

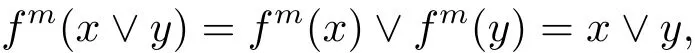
and similarly fm(x∧y)=x∧y.Since x∈T(L)clearly implies f(x)∈T(L),it follows that T(L)is also a subalgebra of L.

Theorem 3.1Let(L;f)∈eD be finitely subdirectly irreducible.Then T1(L)={0,1}.

ProofSuppose that T1(L)contains at least three elements.Then it contains a 3-element chain 0 ＜ a ＜ 1.Then,by Lemma 2.1,we have θ(0,a)= θlat(0,a)and θ(a,1)=θlat(a,1),whence we have the contradiction θ(0,a)∧ θ(a,1)= ω.

Consider now the particular case where L is a finitely subdirectly irreducible symmetry extended distributive lattice.

Lemma 3.1Let L∈e2,0D.Then for x∈L{0,1},either x||f(x),or x=f(x).

Corollary 3.1Let L∈e2,0D be finitely subdirectly irreducible and|L|≥2.Then for x∈L{0,1},x||f(x).

ProofIf x∈L{0,1},then xf(x)according to Theorem 3.1 and so x||f(x)by Lemma 3.1.

Theorem 3.2In the class e2,0D of symmetric extended distributive lattices there are only two( finitely)subdirectly irreducible algebras,each of which is simple,namely,the algebras.

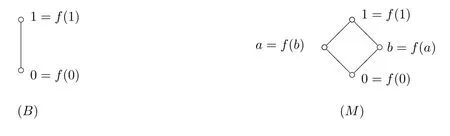
ProofIf|L|=2,then L={0,1}.If|L|=3,let L={0,a,1},then a{0,1}.We have a||f(a)according to Corollary 3.1 and so|L|3,which is absurd.If|L|=4,let L={0,a,b,1},then a,b{0,1}and a||f(a),b||f(b).Thus f(a)=b,f(b)=a.Thus L is M in the above figures.If|L|≥5,then L has 5 distinct points 0,a,b,c,1.If a∧b0,then f(a∧b)0 and a∧b∧f(a∧b)=0,(a∧b)∨f(a∧b)=1 by Theorem 3.1.Since a∧f(a)=0 and b∧f(b)=0,(a∧b)∧f(a∨b)=0 and(a∧b)∨f(a∨b)=1,f(a∨b)=f(a∧b)and so f(a)=f(b),a=b,a contradiction.Thus a∧b=0 and so a∧(f(a)∨b)=0,a∨(f(a)∨b)=1 and therefore

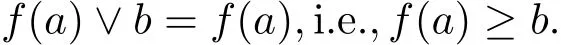
Likely,b∧(f(b)∨a)=0,b∨(f(b)∨a)=1 and therefore f(b)∨a=f(b)and so f(b)≥a and also b≥f(a).Hence we have f(a)=b and so a∨b=1.Also,a∧c=0,a∨c=1.By distributive b=c,a contradiction.

Thus if L is a finitely subdirectly irreducible symmetry extended distributive lattice,then L is only of the two kinds in the above figures.

It is readily seen that for these we have ConB=ConM⋍2.So these algebras are indeed subdirectly irreducible;in fact,they are simple.

Theorem 3.3If L∈eD is such that T1(L)={0,1}and if a,b∈T(L)are such that a ＜ b then θ(a,b)= ι.

ProofFor every x∈T(L),let mxbe the least positive integer such that fmx(x)=x.Consider the elements

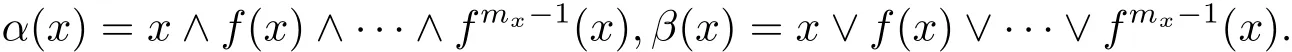
Observe that f(α(x))= α(x)and f(β(x))= β(x),so α(x),β(x)∈ T1(L)={0,1}.Now,let a,b∈T(L)be such that a＜b.Consider the sublattice A that is generated by

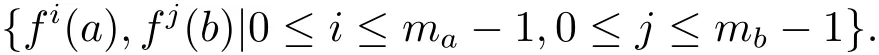
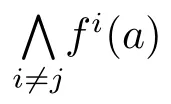
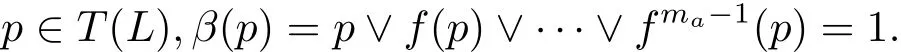
Consequently,A is boolean.

Let c be an atom of A with c/≤ a and c≤ b.Then(0,c)=(a∧c,b∧c)∈ θ(a,b).It follows that(0,f(c))∈ θ(a,b)and so(0,β(c))∈ θ(a,b),i.e.,(0,1)∈ θ(a,b)and therefore θ(a,b)= ι.

Theorem 3.4For an algebra L∈eD the following are equivalent:

(1)T1(L)={0,1};

(2)the subalgebra T(L)is simple;

(3)all symmetric extended distributive sublattices of L are simple.

Proof(1)⇒(2)If(1)holds,then by Theorem 3.3 every non-trivial principal congruence on T(L)coincides with ι.Since every congruence is the supremum of the principal congruences that it contains,it follows that T(L)is simple.

(2)⇔(3)T2(L)is the largest symmetric extended distributive sublattice of L.

(3)⇒(1)If(3)holds,then T2(L)is simple.But T2(L)is a symmetric extended distributive lattice and by Theorem 3.2 there are only two non-isomorphic simple symmetric extended distributive lattices,in each of which T1(T2(L))={0,1}.Since T2(L)and L have the same fixed points,(1)follows.

Theorem 3.5If L ∈ eD is finitely subdirectly irreducible,then every Φ1-class in L contains at most two elements.

ProofSuppose that a Φ1-class contains at least three elements.Then it contains a 3-element chain x ＜ y ＜ z with f(x)=f(y)=f(z).Then,by Lemma 2.1,we have θ(x,y)=θlat(x,y)and θ(y,z)= θlat(y,z),whence we have the contradiction θ(x,y)∧ θ(y,z)= ω.

Theorem 3.6If L∈ep,qD then the following statements are equivalent:

(1)L is finitely subdirectly irreducible;

(2)L is subdirectly irreducible.

Proof(1)⇒ (2)Since L ∈ep,qD,for every x∈ L,we have fp(x)=fq(x).If Φ1= ω,then f is injective and x=fp−q(x),whence x ∈ T(L).Thus L=T(L)and it follows by Theorem 3.1 and Theorem 3.4 that L is simple,hence subdirectly irreducible.

On the other hand,if Φ1ω,then by Theorem 3.5 there is a two-element Φ1-class{a,b},and by Lemma 2.4, θ(a,b)is an atom in the interval[ω,Φ1]of ConL.If now α ∈ConL with αω then,since α is the supremum of the non-trivial principal congruences which it contains and since ConL satis fies the in finite distributive law β∧∨γi= ∨(β ∧γi),it follows by the hypothesis that L is finitely subdirectly irreducible that θ(a,b)∧ α = θ(a,b)and hence θ(a,b) ≤ α.Thus θ(a,b)is the smallest non-trivial congruence on L,so L is subdirectly irreducible.

(2)⇒(1)This is clear.

The following theorem is an extension to eD-algebras of Blyth for Ockham algebras,see[6].

Theorem 3.7L∈ep,qD is subdirectly irreducible if and only if Con L reduces to the finite chain

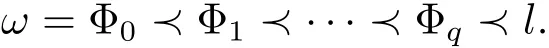
References

[1]Balbes R,Dwinger Ph.Distributive lattices[M].Columbia:Univ.Missouri Press,1974.

[2]Beazer R.Finitely subdirectly irreducible algebras with pseudocomplementation[J].Algebra Universalis,1981,12:376–386.

[3]Gramaglia H,Vaggione D J.(Finitely)subdirectly irreducibles and Birkhoff-like sheaf representation for certain varieties of lattice ordered structures[J].Algebra Universalis,1997,38(1):56–91.

[4]Luo C W,Guo L.On idempotent extended distributive lattices whose congruences are permutable[J].J.Math.,2015,35(2):407–411.

[5]Fang J.Distributive Lattices with unary operations[M].Beijing:Science Press,2011.

[6]Blyth T S,Varlet J C.Ockham Algebras[M].Oxford:Oxford University Press,1994.

[7]Berman J.Distributive Lattices with an additional unary operation[J].Aequationes Math.,1977,16:165–171.

[8]Blyth T S,Jie F.Extended Ockham Algebras[J].Commun.Algebra,2000,28(3):1271–1284.