基于灰色关联模型的城市道路交通拥堵评价研究
(重庆市市政设计研究院,重庆 400020)
0 引言
随着社会经济水平的发展与居民汽车保有量的增加,城市道路交通拥堵问题日渐成为一个普遍存在的问题。城市交通拥堵通常表现为汽车通过某条城市道路或者交叉口时间过长甚至于长时间停留,从而导致行驶时间超过正常水平。为从根源上分析城市道路拥堵原因,需要选取合适的道路拥堵评价指标并构建评价体系,根据科学的交通指标参数对拥堵道路进行分析,从而提出切实可行的城市道路拥堵疏解方案。
国内外专家学者针对城市道路交通拥堵评价问题研究从20世纪80年代开始。Marlon从交通量与通行能力角度定义了评估区域范围拥堵程度的拥堵指数[1]。Mekky构建了基于区域车辆分布的城市交通拥堵评价理论体系,用以评估整个交通网络拥堵状态[2]。祝付玲构建了综合考虑行程时间、排队长度以及可达性等要素的城市道路交通拥堵评价体系[3]。姜桂艳基于宏观、中观、微观三个不同决策角度,构建了城市道路交通拥堵评价体系[4]。张雪莲在评价体系构建中,从时间层面归纳城市交通需求,并通过车辆行驶时间计算评价模型中的指标权重[5]。
以上研究可归纳为基于道路通行能力、排队长度以及行程时间的评价指标。其中,道路通行能力指标通俗易懂、计算方便,故其主要用于评价道路断面拥堵状况以及解释拥堵致因。排队长度指标能从出行者感知角度上反映道路的拥堵状况,但其指标计算数据获取需要大量检测设备。行程时间指标可用于构建模型对路段交通拥堵状况进行量化评估,然而该类指标不适用于不同城市或者不同年份的道路拥堵状况的横向对比。基于以上分析,本文根据各类指标特点,尝试构建更加全面的城市道路交通拥堵评价体系,在此基础上构建基于灰色关联度的城市道路交通拥堵评价模型,旨在为道路运输管理部门提供一定参考。
1 评价体系构建
城市道路交通拥堵评价的最终目的在于环节城市道路拥堵状况,为达到这一目标,需要筛选确定能反映道路拥堵程度的评价指标,对城市道路拥堵进行科学的量化评价,进而提出相应缓解措施。因此,在评价体系构建过程中,需要尽可能保证指标的全面性、客观性以及实用性。
城市道路交通拥堵评价指标包含宏观、中观以及微观三个层面,其中宏观层面是指城市道路交通网相关指标,中观层面是指道路路段与交叉口相关指标,微观层面是指运行车辆相关指标。因此,城市道路交通拥堵评价体系主要包括区域指标、路段指标以及交叉口指标三个类别。
1.1 交叉口指标
根据城市道路交叉口的功能及交通特性,交叉口评价指标包括:交叉口交通量V(当量小汽车/小时)、饱和度S、平均延误时间d(秒)、排队长度q、信号交叉口二次排队率κ、效率指数I,其计算方法详见文献[5]。
1.2 路段指标
根据城市道路路段交通特性,路段指标包括路段交通量Q(veh/h)、路段长度L(km)两个基础指标,可以通过直接测量得到;还包括路段行驶时间tL(min)、路段平均速度v(km/h)、出行速率u(min/km)、可接受出行时间tLa(min)、可接受出行速率ua(min/km)、延误时间dL(min)、总延误DL(min·veh),其计算方法详见文献[5]。
1.3 区域指标
区域指标包括区域机动性指数MI、拥堵道路长度Lc(km)、拥堵出行量Cn(min·veh)以及可达性Ab,其计算方法详见文献[5]。
遵循系统综合评价的层次性原则、实用性原则以及可操作性原则,构建城市道路交通拥堵评价体系如图1所示。

图1 城市道路交通拥堵评价体系
2 指标权重确定
在工程评价问题中,首先要对评价体系中的各个指标赋予权重以反映各个指标的重要程度,权重确定的合理与否往往决定了综合评价结果是否科学客观。较为常用的指标权重确定方法包括专家打分法、德尔菲法以及层次分析法,但上述方法主要依靠人工决策,具有较强的主观性。近年来,信息熵概念逐渐被应用于工程领域的各个学科,熵值是一种描述系统无序程度的量化值,在综合评价中可用熵值量化描述各个指标提供给决策者的信息量,并根据信息量来赋予各个指标的权重,从而使得指标权重更加客观合理。
基于信息熵的指标权重计算方法如下:
Step1:假设被评价对象(城市道路)包含m个评价指标,根据其统计的n年道路交通拥堵状况构建样本矩阵

一般而言,评价指标包括效益性指标及成本型指标两类,前者是指数值越大效果越好的指标,后者是指数值越小效果越好的指标,上述两种指标无量纲处理公式为:
效益性指标

成本性指标

样本矩阵无量纲化处理后得矩阵Y=(yij)nxm;
Step2:根据如下公式计算评价指标j的熵值

式中,k=1/ln m;
Step3:根据如下公式计算评价指标j的熵权ωj

通过对统计数据结果进行归一化处理,并按照上述步骤计算得到各指标权重值及排序如表1所示。
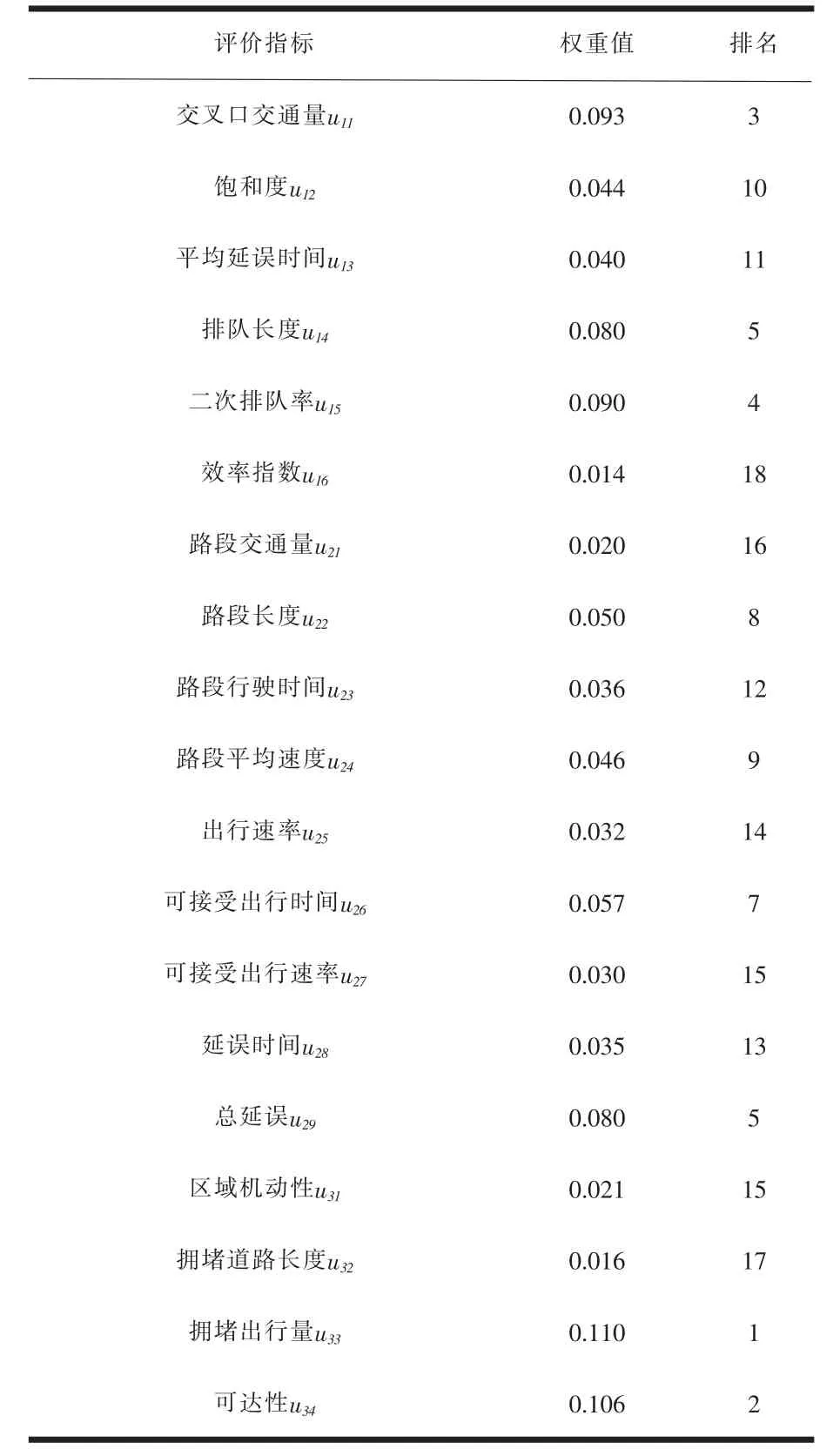
表1 评价体系中各因素权重及综合排序
3 灰色关联评价模型
3.1 最优向量构建
根据灰色关联性相关理论,构建城市道路交通拥堵评价指标最优向量如下:
G=(g1,g2,…,gm)
此处G表示由上述m个评价指标最优质所组成的最优向量,需要额外说明的是,由于各个指标均存在一个基准值,如果效益型指标的实际值大于基准值,则该指标的最大值取值应为基准值,如果成本型指标的实际值小于基准值,则该指标的最小值取值应为基准值。
3.2 灰色关联系数确定
计算评价指标Yj与G最优向量的关联系数ζi(Yj,G),计算公式如下:

式中为样本两级的极小差;为样本两级的极大差;ρ∈(0,∞)为分辨系数,其值越小,分辨能力越大。
计算评价对象与最优向量G的综合关联度R,即城市道路交通拥堵指数:

4 实例分析
选用重庆市南岸区的某个路段城市道路网络作为综合评价的实例,根据前文构建的城市道路交通拥堵评价体系及评价模型,并根据2011-2016年统计数据计算各评价指标与基准值之间的关联度,将其汇总就得到2011-2016年的城市道路交通拥堵综合指数,如表2所示。限于篇幅文中仅列举部分数据。同理根据公式(7),分别计算上述几年交叉口指数、路段指数以及区域指数值,如表3所示。
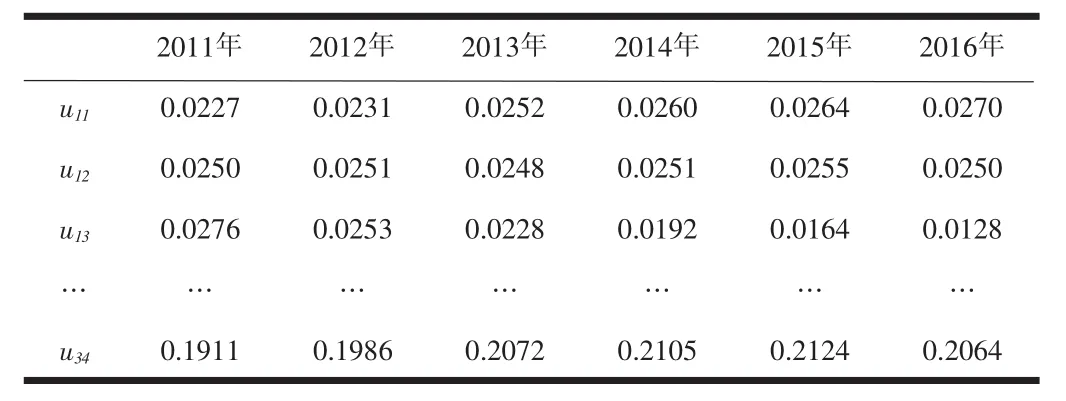
表2 重庆市南岸区某路段城市道路拥堵指标指数

表3 重庆市南岸区某路段城市道路拥堵综合指数
根据城市道路拥堵综合指数变化趋势,并结合道路拥堵指标评分标准[6],该路段自2011年以来,交叉口指数、路段指数以及区域指数在整体上均呈现波动上升趋势,与城市道路交通的发展趋势较为吻合。
从交叉口指标来看,2011-2016年该类指标指数基本维持在0.63左右,各个年度指数相差较小,均处于一般状态。
从路段指标来看,该类指标指数从2011年的0.5520持续稳步上升到2016年的0.6675,增幅达到21%,路段拥堵现状趋于好转。
从区域指标来看,该类指标指数在整体上呈波动上升趋势,但增速较小,数值均低于0.55,处于较差状态,响应力度不足。
各年的道路拥堵综合指数均在0.50~0.70,说明该路段城市道路拥堵状况变化不大,综合评价结果仍处于一般状态。
5 结论
本文构建了包含有交叉口指标、路段指标以及区域指标的城市道路交通拥堵评价模型,并结合信息熵赋权法与灰色关联分析法对重庆市南岸区某路段的城市道路拥堵等级进行量化评价,较大程度地避免了人工主观因素对评价结果的干扰,能更加真实地反映被评估路段的拥堵水平,为进一步研究城市道路拥堵的疏解方案提供科学的决策依据。
参考文献:
[1]Boarnet,Kim,Parkany.Measuring traffic congestion[J].Transportation Research Record,1998,1634:93-99.
[2]Mekky.Measuring Congestion in the Greater Toronto Area[C].83rd Annual Meetings of the Transportation Research Board,Washington,D.C.,2004.
[3]祝付玲.城市道路交通拥堵评价指标体系研究[D].南京:东南大学,2006.
[4]姜桂艳,郭海锋,孟志强,等.基于实时信息的城市道路交通状态评价指标体系研究[J].交通与计算机,2007(5):21-24.
[5]张雪莲,于雷,刘梦涵.基于交通需求的路网交通拥堵评价模型[J].现代交通技术,2008(6): 71-75.
[6]美国交通研究委员会TRB.道路通行能力手册(精)[M].福田,刘小明,荣建,等译.北京:人民交通出版社,2007:197-199.

