破裂砂岩冲击破坏特性研究

刘 洋，潘 康，周新贵

(1.建筑结构与地下工程安徽省重点实验室(安徽建筑大学)，安徽 合肥 230601；2.安徽建筑大学 土木工程学院，安徽 合肥 230601；3.安徽宏源电力建设投资有限公司，安徽 合肥 250013)

交通隧道、水电地下厂房、矿产资源开采等地下工程施工过程中，工作面和巷道开挖引起周边围岩应力重新分布，导致工作面和巷道周边一定范围内的围岩处于破坏状态，成为断续结构，破坏后的围岩依然具有一定的承载能力，对支撑工作面和巷道稳定起着十分重要的作用。但是由于受爆破、地震等动力荷载作用，已开挖的处于稳定状态的工作面和巷道周围断续破裂岩体仍然存在失稳的安全隐患[1]，因此，研究破裂岩体的冲击破坏特性具有重要的工程实践意义。

目前，国内外学者对完整岩石动态破坏特性进行了广泛的研究并取得许多有价值的研究成果[2-3]，同时对含软弱结构面岩体、断续破裂岩体等动态破坏特性也开展了相关的探索。李夕兵等[4-7]分析研究了节理、裂隙对应力波传播的影响；王林等[8-11]采用SHPB实验装置或伺服材料试验机对模型预制裂隙试样进行了动力学试验研究；祝文化等[12]采用SHPB实验装置对爆破破裂影响区内的损伤岩体和爆破破裂影响区外的完整岩体进行了冲击压缩试验研究；朱万成等[13-16]采用数值计算方法对预制裂隙岩体、缺陷岩体等动力学特性进行数值模拟研究。上述研究成果对认识断续破裂岩石动态破坏特征具有重要意义，但是不难发现，关于断续破裂岩石的动态破坏特性主要采用模型预制裂隙和数值计算两种方法，而真实断续破裂岩石材料的动态破坏特性研究则鲜见报道。

本文通过对完整砂岩试样进行静态加载，在岩石应力刚过其峰值时进行卸载，从而形成峰后破裂砂岩试样，然后采用SHPB实验装置对峰后破裂砂岩试样进行单轴冲击压缩试验，研究峰后破裂砂岩的冲击破坏特性，为地下工程设计与施工提供参考。

1 试样制备及试验设备

1.1 试样制备

在同一砂岩大块上沿同方向钻取Ø50mm的圆柱形试样，制备完整砂岩试样，如图1(a)所示。为保证SHPB实验时岩石试样径向方向上应力均匀，且考虑完整砂岩试样需要在静载试验机上进行静态加载制作峰后破裂砂岩试样，按照岩石动力学试验建议方法的要求试样长径比选为1，试样两端面不平行度和不垂直度均小于0.02mm[17]。

制作峰后破裂砂岩试样时，采用MTS815岩石力学试验系统对完整砂岩试样进行单轴压缩。加载初期采用应力控制，接近峰值时转化为位移控制，以平稳越过峰值，在岩石应力越过其峰值时进行卸载，形成峰后破裂砂岩试样，如图1(b)所示。

破裂砂岩试样外观基本保持完整，但内部已遭受破坏，通过CT扫描可以推断破裂砂岩内部裂隙形态如图1(c)所示。

1.2 试验设备

试验采用杆径为50mm的SHPB实验装置，如图2所示。该实验装置的入射杆、透射杆、吸收杆和冲头均采用40Cr合金钢，密度为7810 kg/m3，纵波波速为5 400 m/s。发射腔内采用纺锤形冲头以消除PC振荡，实现恒应变率的半正弦应力波加载。数据采集采用CS-1D超动态应变仪和DL-750示波器。

图2 霍普金森压杆实验装置

2 试验结果与分析

2.1 峰后破裂砂岩试验结果

峰后破裂砂岩试验结果如表1所示，从表中可以看出：不同应变率下峰后破裂砂岩变形模量是离散的，这可能是因为峰后破裂砂岩本身存在因静态压缩形成的随机裂纹，裂纹对外部冲击的反应不同导致变形模量不同。

表1 峰后破裂砂岩冲击试验结果

2.2 应力-应变曲线

不同应变率下峰后破裂砂岩和完整砂岩应力-应变曲线如图3所示，从中可以看出：峰后破裂砂岩应力-应变曲线与完整岩石应力-应变曲线相类似，当应变率较小时，峰后曲线出现反弹的现象，随着应变率的增大，峰后曲线反弹的现象逐渐减少。

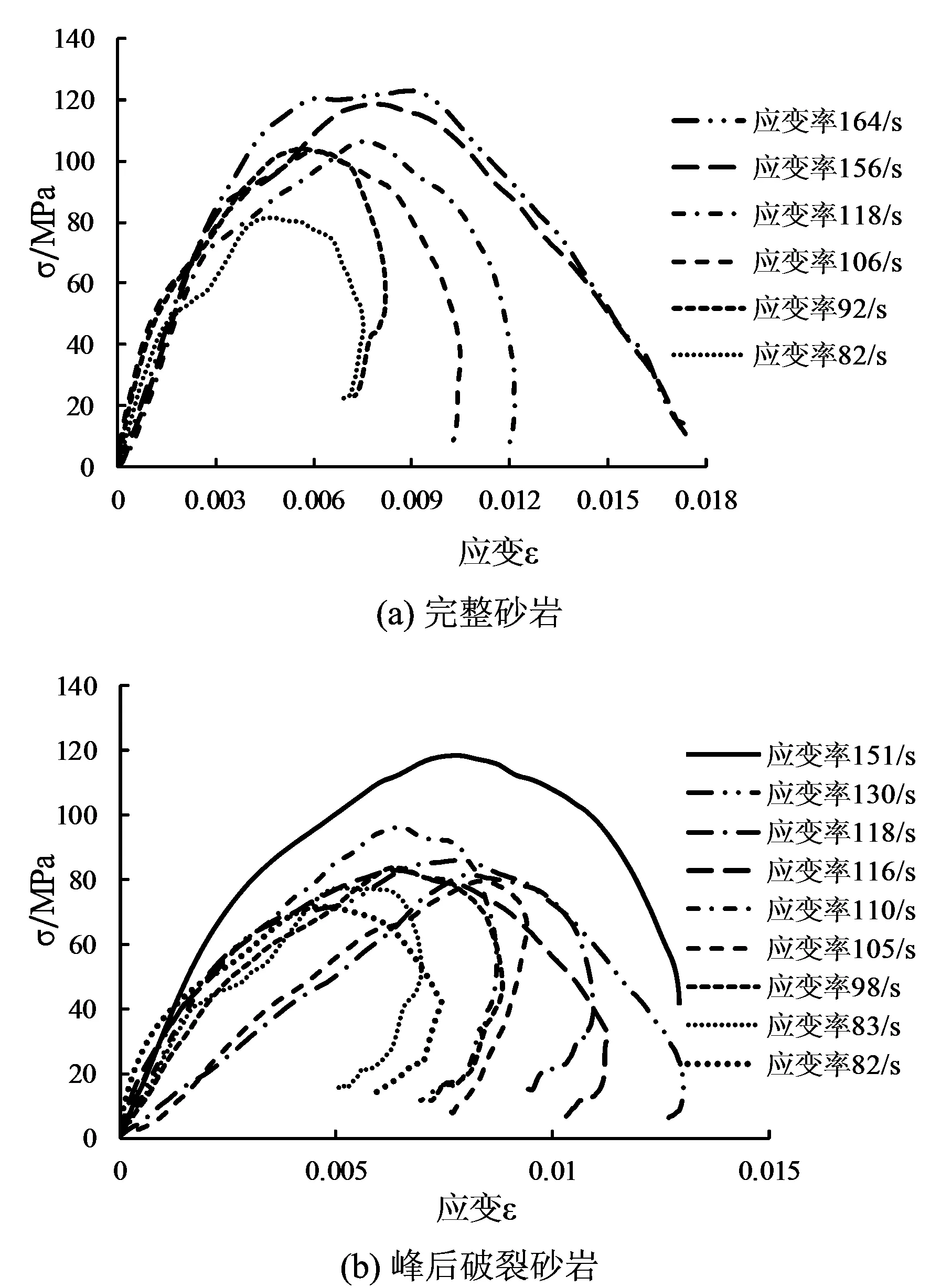
图3 不同应变率下砂岩应力-应变曲线

为更好地了解冲击荷载作用下砂岩应力-应变曲线，选取一条曲线进行分析，图4为典型应力-应变曲线。

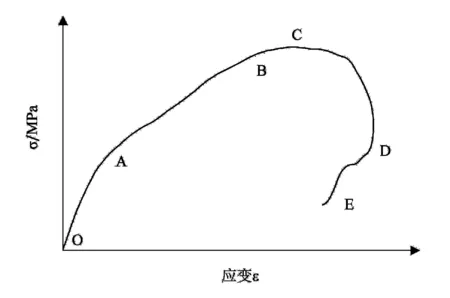
图4 典型应力-应变曲线

从图4中可以看出典型应力-应变曲线大致可以分为以下几个阶段：

1)OA段：该段曲线与静态应力-应变曲线初始段不同，未表现出下凹型。加载初期，应力急剧增加，内部裂纹来不及贯通，岩石初始弹性模量较大。

2)AB段：该段应力-应变曲线与静态时微裂纹扩展阶段相似，内部裂纹增多，导致弹性模量降低。

3)BC段：该段应力-应变曲线与静态时非弹性变形破坏阶段相似，裂纹在冲击荷载作用下不断破裂发展，导致弹性模量降低，直至岩石试样破坏，C点为岩石试样的峰值强度。

4)CD段：试样到达峰值强度，内部遭受破坏，大量新的裂纹产生、扩展、汇合，裂纹快速发展，试样破坏，导致试样承载能力迅速降低。

5)DE段：试样破坏，承载能力下降，但是并未完全失去承载力，当加载应力小于岩石残余承载能力时，试样变形出现反弹，应变减小。

对于DE段，当应变率足够大时，应力加载阶段导致试样完全破碎，没有残余承载能力时，则不会出现变形反弹，应变减小的现象。

同时，从图3(b)中不难发现应变率为105/s(试样5-3)和118/s(试样5-4)的试样应力-应变曲线与其他试样的曲线有些差异。加载初始阶段与静态加载初始段一样的下凹型，可能是因为峰后破裂砂岩存在裂纹，冲击加载初期，裂纹首先被压密闭合，与岩石静态加载初期试样内部原有缺陷、微裂纹被压密闭合类似，因此，出现下凹型曲线。

与试样5-3与5-4相比，承受更低应变率冲击的试样应力-应变曲线也未呈现下凹型初始段，这可能是因为试样5-3与5-4峰后卸载点强度(峰后破裂砂岩制备时，越过峰值后卸载点的强度)相比较其他试样更低，试样破坏更加严重，裂纹张开度更大。即使承受更大应变率的冲击荷载，裂纹首先被压密闭合，而其他试样破坏较小，承受冲击荷载时，裂纹来不及闭合，因此，曲线未出现下凹型初始段。

2.3 动态强度

冲击荷载作用下岩石强度得到提高已经取得了学术与工程界的共识，峰后破裂砂岩与完整砂岩动态强度-应变率的关系曲线如图5所示。

图5 动态强度-应变率关系曲线

由图5可知：在试验所处的应变率范围内，完整砂岩的动态强度随着应变率的增大而增大，表现出明显的应变率效应。峰后破裂砂岩动态强度试验结果比较离散，但总体还是随着应变率的提高而增大，特别是应变率为151/s的试样动态强度增幅明显。

为了更好地研究应变率对峰后破裂砂岩动态强度的影响，采用岩石动态强度增幅系数(峰后破裂砂岩动态强度相比较于其静态压缩峰后卸载点强度的差值与峰后卸载点强度的比值)来代替动态强度进行分析。不同应变率下峰后破裂砂岩动态强度增幅系数如图6所示。

图6 动态强度增幅系数-应变率关系曲线

从图6可以看出：应变率为82/s和83/s的峰后破裂砂岩动态强度增幅系数小于10%，应变率98/s～130/s范围内峰后破裂砂岩动态强度增幅系数介于20%～33%之间，而应变率为151/s时增幅系数为59.4%，分析动态强度增幅系数逐渐增大的原因，可能是因为应变率低时，冲击入射能主要用于裂纹的扩展，加剧了破裂砂岩的损伤，导致岩石承载能力增加较慢，而高应变率时，冲击压缩时裂纹扩展速度比岩石承载能力增加速度低，因此，峰后破裂砂岩强度增幅较大。

2.4 峰值应变

不同应变率下峰后破裂砂岩和完整砂岩峰值应变与应变率的关系曲线如图7所示。

图7 峰值应变-应变率关系曲线

由图7可以看出：在试验所处的应变率范围内，峰后破裂砂岩和完整砂岩峰值应变均随着应变率的增大而增大，这与冲击强度也随应变率变化的规律是一致的；且相近应变率下，峰后破裂砂岩峰值应变大于完整砂岩峰值应变。

2.5 破坏模式

图8 完整砂岩破坏形态图

图8为单轴冲击荷载作用下完整砂岩破坏形态图，从中可以看出：完整砂岩破裂面平行于试样轴向方向，破裂面表面未出现摩擦滑移的痕迹，且原始裂纹部位破坏程度更严重。典型碎块两端大小相近，破碎块度较为规整，破裂面有些凸凹不平，这是因为岩石破坏时，晶体和胶结物质张裂分离的结果[18]；破裂面表面无岩粉分布，说明无摩擦滑移，由此可以推断完整砂岩破坏模式为劈裂破坏。

图9为单轴冲击荷载作用下峰后破裂砂岩破坏形态图，从中可以看出：峰后破裂砂岩破坏形态与完整砂岩破坏形态相同，破裂面平行于试样轴向方向，且破裂面表面未出现摩擦滑移的痕迹。但是，部分碎块的形状与完整砂岩破坏碎块的形状有所不同，峰后破裂砂岩典型破裂碎块成锥状，这可能是因为峰后破裂砂岩内部含有因静态加载形成的潜在剪切面，在冲击荷载作用下破裂面沿着剪切面继续扩展；而破裂面表面无岩粉分布，表明未发生摩擦滑移现象，由此可以推断峰后破裂砂岩破坏模式也是劈裂破坏，且已有裂纹影响破裂面扩展方向。

图9 峰后破裂砂岩破坏形态图

3 结论

采用SHPB实验装置对峰后破裂砂岩进行单轴冲击试验，研究峰后破裂砂岩冲击破坏特性，得到以下主要结论：

1)与完整岩石实验结果相比，由于受静态加载产生的裂纹的影响，峰后破裂砂岩变形模量比较离散；且导致部分内部破裂严重的峰后破裂砂岩应力-应变曲线初始阶段出现下凹现象。

2)峰后破裂砂岩动态强度和峰值应变随着应变率的增大而增大，且相近应变率下破裂砂岩动态强度低于完整砂岩动态强度。

3)单轴冲击荷载作用下峰后破裂砂岩为劈裂破坏，但受原始裂纹的影响，裂纹扩展沿原始裂纹方向发展，且原始裂纹部位破坏程度更严重。

参考文献：

[1]姜耀东，潘一山，姜福兴，等.我国煤炭开采中的冲击地压机理和防治[J].煤炭学报，2014，39(2)：205-213.

[2]黄理兴.岩石动力学研究成就与趋势[J].岩土力学，2011，32(10)：2889-2900.

[3]ZHANG Q B, ZHAO J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials[J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1411-1478.

[4]李夕兵.论岩体软弱结构面对应力波传播的影响[J].爆炸与冲击，1993，13(4)：334-342.

[5]JU Yang, Sudak Les, XIE Heping. Study on Stress Wave Propagation in Fractured Rocks with Fractal Joint Surfaces[J]. International Journal of Solids and Structures, 2007(44): 4256-4271.

[6]LI J C, MA G W. Experimental Study of Stress Wave Propagation Across a Filled Rock Joint[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(1):471-478.

[7]LI Yexue, ZHU Zheming, LI Bixiong, et al. Study on the Transmission and Reflection of Stress Waves Across Joints[J]. International Journal Rock Mechanics & Mining Sciences, 2011(48): 364-371.

[8]王林，于亚伦.裂隙矿岩的动载特性[J].北京科技大学学报，1994，16(2)：101-105.

[9]张平，李宁，贺若兰，等.动载下3条断续裂隙岩样的裂缝贯通机制[J].岩土力学，2006，27(9)：1457-1464.

[10]张海波.动、静荷载作用下不同倾角裂隙岩体力学性能试验模拟研究[D].南京：河海大学(硕士学位论文)，2007.

[11]刘红岩，邓正定，王新生，等.节理岩体动态破坏的SHPB相似材料试验研究[J].岩土力学，2014，35(3)：659-665.

[12]祝文化，李元章.损伤灰岩动态压缩力学特性的实验研究[J].武汉理工大学学报，2006，28(7)：90-92.

[13]朱万成，逄铭璋，唐春安，等.含预制裂纹岩石试样在动载荷作用下破裂模式的数值模拟[J].地下空间与工程学报，2005，1(6)：856-858.

[14]刘红岩，王贵和.节理岩体冲击破坏的数值流形方法模拟[J].岩土力学，2009，30(11)：3523-3527.

[15]左宇军，唐春安，李术才，等.基于大直径霍普金森压杆数值试验的非均匀介质动态破坏过程分析[J].岩土力学，2011，32(1)：230-236，268.

[16]朱哲明，李元鑫，周志荣，等.爆炸荷载下缺陷岩体的动态响应[J].岩石力学与工程学报，2011，30(6)：1157-1167.

[17]ZHOU Y X, XIA K, LI X B, et al. Suggested Methods for Determining the Dynamic Strength Parameters and Mode-I Fracture Toughness of Rock Materials[J]. International Journal Rock Mechanics & Mining Sciences, 2012(49): 105-112.

[18]金解放.静载荷与循环冲击组合作用下岩石动态力学特性研究[D].长沙：中南大学(博士学位论文)，2012.