基于经验模态分解-自回归组合模型的网络舆情预测
莫 赞,赵 冰,黄艳莹
(广东工业大学 管理学院,广州 510520)
0 引言
随着网民规模的不断扩大,互联网已成为除报纸、广播、电视等传统媒体外的又一信息传播的重要途径。目前,国内的微信、微博、论坛、贴吧和新闻网站等借助互联网平台的社交媒体或网站已成为信息传播的重要战场。日益增多的网民接收着来自现实世界和虚拟世界的各种信息,并在社交媒体等上畅所欲言,发表对于社会事件的看法和意见。当突发的网络事件或社会事件引起网民广泛关注时,它将演化为网络舆情,并对社会公共安全和长期发展造成重大影响[1-3]。此外网络推手幕后炒作、网络暴力和网络谣言会影响并导致网络舆情事件失控变质,影响社会安全稳定和长期发展[4-5]。因此,网络舆情的演化规律研究和预测对于舆情工作的开展和管控具有重要意义,有助于政府部门和企业以积极主动的方式面对舆情工作。
处于大数据时代之中,舆情信息工作需要采集的数据量庞大,同时,社交媒体、新闻媒体、搜索引擎等网络平台使得网络传播呈现一种“蜂窝状”的发散性结构,致使分析预测网络舆情的难度加大;而且预警时间随着舆情事件的爆发而呈现不稳定的状态,这些问题使得网络舆情的应对工作面临更大的挑战[6]。
网络舆情通常是通过时间序列的方式进行记录。网络舆情数据一般是来自于短期内舆情萌芽、爆发、消亡等过程,所以舆情数据一般具有非线性、非平稳、动态等特征[7]。采用数据挖掘方法和相关科学理论预测舆情时间序列,能更好地解决这一问题,常用的方法主要有贝叶斯网络模型[8]、灰色理论[9]等。然而这些单一模型的预测能力有限,面对复杂的舆情数据时不能有效地进行预测。常用的处理方式是将时间序列模型与数据挖掘模型相结合,构建更准确的组合预测模型[10]。组合预测模型克服了单一预测算法的缺点, 能发挥各个单一预测模型的优势,进而提高模型整体的预测精度。本文提出了一种新的组合预测模型——EMD-ARXG(Empirical Mode Decomposition-AutoRegression based on eXtreme Gradient boosting)模型,用于复杂网络舆情的预测。
1 相关理论
网络舆情时间序列是非平稳的时间序列,难以用经典的时间序列方法预测未来序列。来自于信号处理领域的经验模态分解(Empirical Mode Decomposition, EMD)算法,为非平稳的时间序列提供了新的分解变换思路。EMD的基函数是由数据本身分解得到,是后验的;又由于分解是基于信号序列时间尺度的局部特性,因此EMD算法具有自适应性,不需要人为设定基函数,更便于预测建模[11]。
复杂的时间序列通过EMD分解成数目有限的本征模态函数(Intrinsic Mode Function, IMF)之和。分解得到的IMF序列能够很好地刻画原始时间序列在每个局部的振荡,具有性能良好的Hilbert变换,从而得到Hilbert谱。IMF需满足两个条件:
1)在数据集中,极值点的数量与过零点数量必须相等或最多相差一个。
2)在任一点上,由所有局部极大值点确定的上包络线和所有局部极小值点确定的下包络线的均值为零。
依据IMF的定义,分解得到时间序列的上包络和下包络是关于时间轴对称的(简称包络对称)。分别通过对序列的极大值点和极小值点进行三次样条插值产生时间序列的上包络和下包络。如果分解得到的序列不是IMF,则上下包络是不对称的。用emax(i)表示第i个时间数列数据的上包络,emin(i)表示下包络,若包络不对称,则有如式(1)所示:
emax(i)+emin(i)≠0
(1)
据此得到包络均值,如式(2)所示:
(2)
当包络对称时m(t)等于0,否则m(i)不等于0。为满足包络对称,一种基于经验的做法是将不为零的m(t)从时间序列中剔除,若得到的时间序列仍不关于时间轴对称,则重复上述过程,直到满足IMF的两个必要条件。IMF的计算过程就是EMD对时间序列进行筛分的过程。筛分过程产生的IMF是基于经验的,目前还未有严格的数学理论进行推理支撑,故该方法称为经验模态分解。
对于分解后的舆情数据,需要利用一定的预测模型进行预测。自回归(AutoRegression, AR)模型是经典的时间序列预测模型之一[12],用以描述当前预测值与历史值之间的关系,适合短期预测,主要以时间序列本身的特性进行预测,所以AR模型适于对EMD分解后的时间序列进行建模预测。
对于时间序列{x(i),i=1,2,…,N},在利用自身作为回归变量时,一般形式的数学模型如式(3)所示:
xi+1=φ1xi+φ2xi-1+…+φpxi-p+1+ξi+1
(3)
其中:N表示时间序列的数据总量,{φj=φ1,φ2,…,φp}是回归模型的参数,ξi+1是均值为0、方差为σ的白噪声序列。p为组成线性模型的自变量个数,p阶自回归模型即为含有p个滞后量的线性组合。
AR模型在建模和预测中难免存在一定误差,对于复杂的舆情数据,更需要一定措施避免较大误差。Friedman等[13]提出极限梯度提升(eXtreme Gradient Boosting, XGBoost)算法用于时间序列预测的思想。XGBoost算法作为梯度提升算法的一种,内置交叉验证,并具有训练速度快、模型交互性好等优点[14],可对AR预测模型的残差进行学习,降低AR模型的预测误差[15-16]。
XGBoost算法在用于残差学习过程中需要设定目标函数如式(4)所示:
(4)
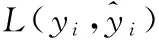
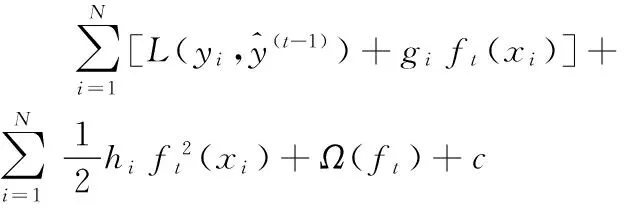
(5)
其中t表示第t轮训练,gi和hi为:
(6)
(7)
XGBoost 算法使得求解的目标函数只依赖于每个数据点在误差函数的一阶导数和二阶导数,可以高效针对这种情况。
EMD-ARXG模型结合EMD算法和AR模型的各自特点和优势,首先使用EMD算法对时间序列进行分解;再利用AR模型对各个子时间序列的进行趋势拟合,建立子模型;最后再对各个子模型进行EMD重构。
2 EMD-ARXG模型
复杂的时间序列的影响因素较多,难以量化和趋势预测。在AR建模过程中,结合XGBoost算法,对AR模型的预测误差进行学习,并获取模型损失函数值。结合损失函数值对AR模型进行迭代更新,最终获取高精度EMD-ARXG预测模型。EMD-ARXG模型框架如图1所示。具体模型建立流程如下。
步骤 1 执行EMD算法,对时间序列{x(i),i=1,2,…,N}进行分解。
1)找出时间序列中的极大值emax(i)和极小值emin(i)。
3)将m(i)从时间序列中剔除,得到差序列:
h(i)=x(i)-m(i)。
4)求解差序列h(i)的限值标准差SD值:
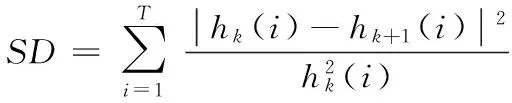
(8)
其中:T为当前筛选序列长度,hk(i)为第k次筛选得到的数据序列。
5)判断hk(i)是否为IMF分量。若SD值符合预定值,一般为0.2~0.3,则是IMF分量。若不是,重复子步骤1)~4)直到所得到的平均曲线趋于零为止。
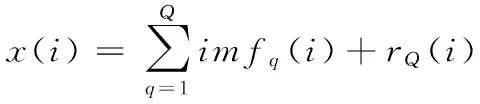
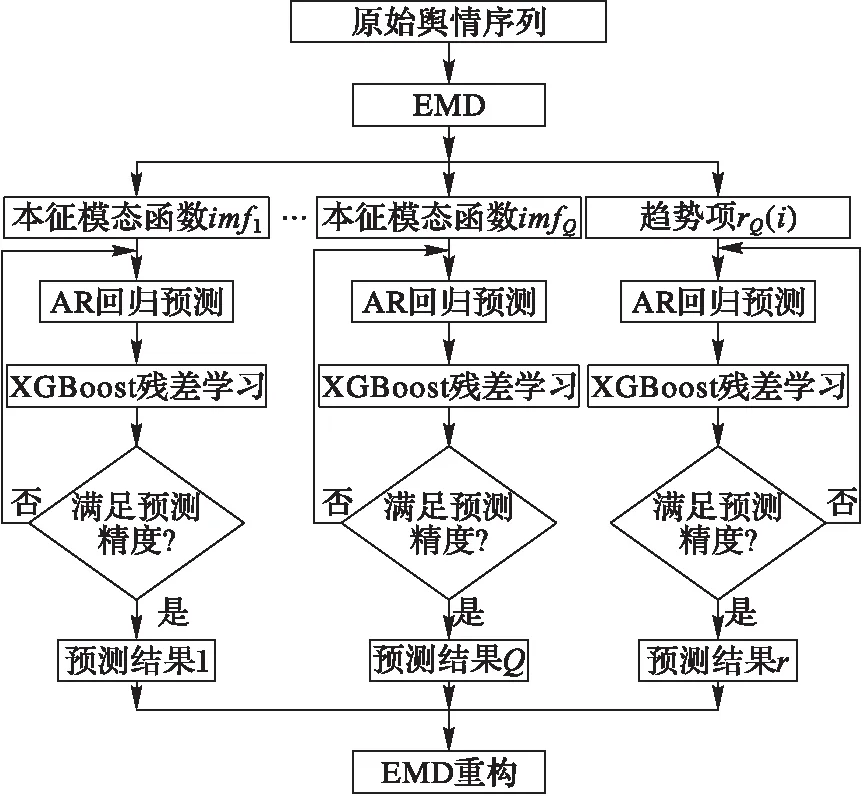
图1 EMD-ARXG模型框架 Fig. 1 Framework of EMD-ARXG model
步骤2 基于XGBoost对分解后的时间序列建立各个子AR模型。
1)对各个子时间序列进行建立AR模型。
3)通过比较目标函数的目标值与设定误差值的大小,从而判断是否达到模型的预测效果。若满足进行下一步,若不满足,则更新AR。
步骤3 对各个子AR模型进行EMD重构,完成建模。
3 实验研究
3.1 实验数据
本文研究两个不同的舆情热点事件为2016年里约奥运会和2017年一带一路,使用两个舆情事件的关键词“里约奥运会”和“一带一路”获取各自的百度指数和微指数。对于里约奥运会,舆情时间段为2016年08月01日至2016年08月31日,共31天。对于一带一路,舆情时间段为2017年04月29日至2017年05月29日,共31天。两个事件的舆情趋势如图2、3所示。本文预测采用滚动式方法, 即 5 天为一个周期,用前 5 天的时间序列进行第 6 天的预测。对于每个事件中的每个指标,最终获得26组数据,取前16组数据用于训练模型,后10组数据用于预测。
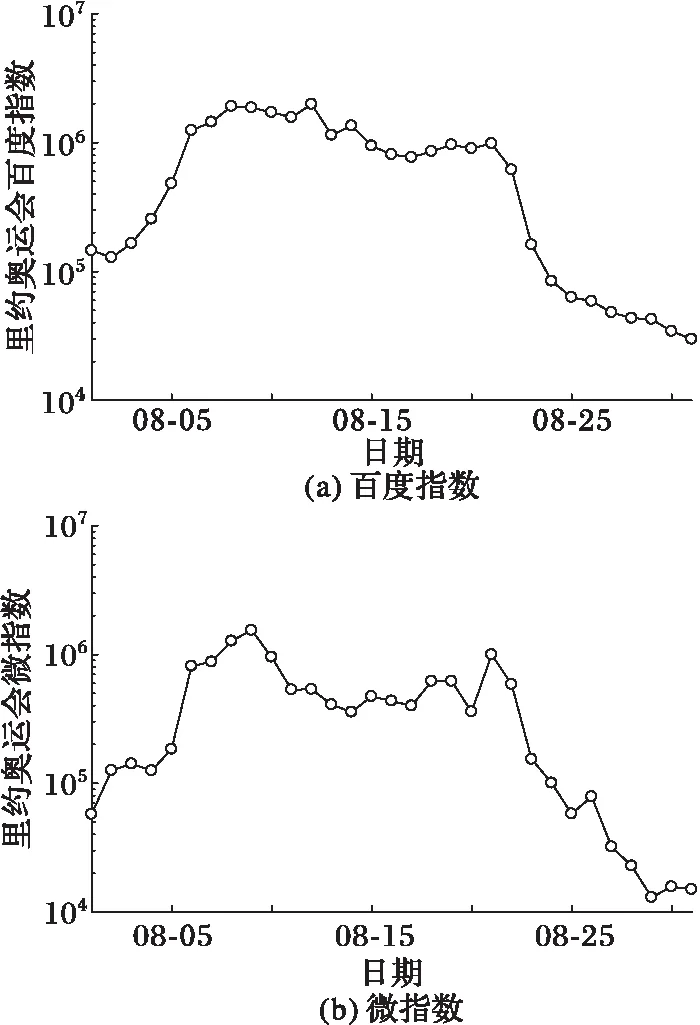
图2 2016年里约奥运会走势 Fig. 2 Trend of Rio Olympic Games in 2016
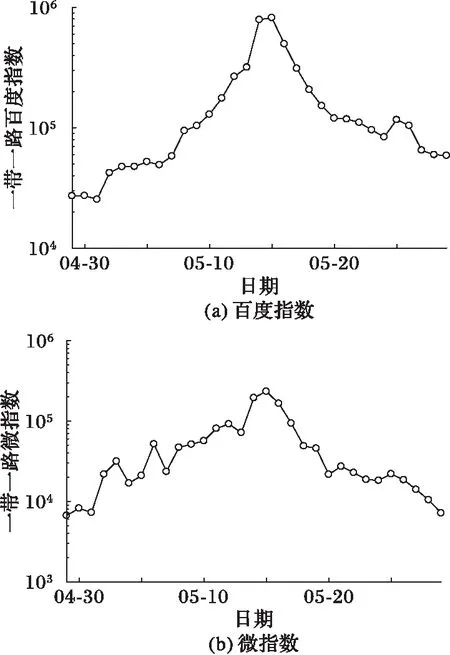
图3 2017年一带一路走势 Fig. 3 Trend of the Belt and Road in 2017
两个指数的计算方式不一致,导致指数大小差异较大,因而,对舆情数据进行规范化处理。规范化可以提高预测模型中梯度下降的最优求解速度,利于算法收敛。规范化的方法是将时间序列数据的值限定在区间[0,1]内,对于时间序列采用最小最大标准化公式:
(9)
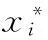
3.2 实验对比分析
为验证EMD-ARXG模型对复杂舆情趋势的预测效果,用小波神经网络(Wavelet Neural Network, WNN)和基于经验模态分解的BP神经网络模型(Back Propagation Neural Netork based on Empirical Mode Decomposition, EMD-BPNN)模型同时对以上舆情进行预测。其模型设置如下:
1)WNN模型参数设置。模型进行随机初始化,采用小波基作为激活函数,神经网络学习率分别设置为0.01和0.001,最大迭代次数设置为1 000,隐含层神经元个数设置为测试效果较好的4。
2)EMD-BPNN模型设置。因所研究舆情事件时间长度较短,初始时间序列用EMD分解为3个本征模态函数imf和一个趋势项r。另外,隐含层神经元个数设置为测试效果较好的16。
3)EMD-ARXG模型参数设置。与EMD-BPNN模型相同,初始时间序列用EMD分解为3个本征模态函数imf和一个趋势项r。另外,XGBoost算法采用的梯度提升模型为线性函数,学习率为采用默认值0.3,算法学习目标为线性回归,XGBoost算法的其他相关参数采用默认值。
采用3个预测模型对4组舆情数据进行拟合预测,拟合结果如图4、5所示。可以看出:WNN的各拟合线明显偏离真实趋势线,EMP-BPNN拟合结果较为接近真实趋势线;但是,相比前两个模型,EMD-ARXG模型的拟合线可以更好地逼近真实趋势线。从最后一天的指数预测可以明显看出,相比WNN和EMD-BPNN模型,EMD-ARXG模型的预测值总体更接近于真实值。
本文对预测结果进行相应的均方根误差(Root Mean Square Error, RMSE)、平均绝对百分误差(Mean Absolute Percentage Error, MAPE)和希尔不等系数(Theil Inequality Coefficient, TIC)指标进行统计,其结果如表1所示,并对各个指标数据进行分析,如下:
1)RMSE指标分析。由于本文采用的舆情数据值较大,因此对应的均方根误差也相对较大。除一带一路的百度指数外,EMD-ARXG模型的RMSE值在其余5组实验中全是最小的,表明该模型的预测效果较好。而WNN模型所有的RMSE值都高于EMD-BPNN模型和EMD-ARXG模型的RMSE值。
2)MAPE指标分析。 除一带一路的百度指数外,EMD-ARXG模型的MAPE值在其余5组实验中是最小的,但是在 一带一路的百度指数对比中,EMD-ARXG模型的MAPE值与EMD-BPNN模型的MAPE值相近。总体而言,WNN模型与EMD-BPNN模型的MAPE值较高,说明预测精度低于EMD-ARXG模型。
3)TIC指标分析。从TIC值可以看出,EMD-BPNN模型仅在一带一路的百度指数上取得TIC值最小值,其余都是EMD-ARXG模型取得最小值。所以相比WNN和EMD-BPNN模,EMD-ARXG模型更适于舆情事件的趋势预测。
综合分析,EMD-ARXG模型的各个预测模型评价指标是3个模型中最佳的,拟合效果和预测精度都高于WNN和EMD-BPNN模型。
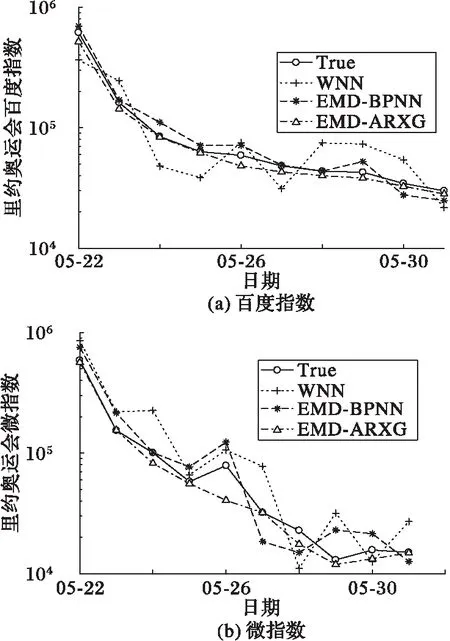
图4 2016年里约奥运会预测 Fig. 4 Prediction of Rio Olympic Games in 2016
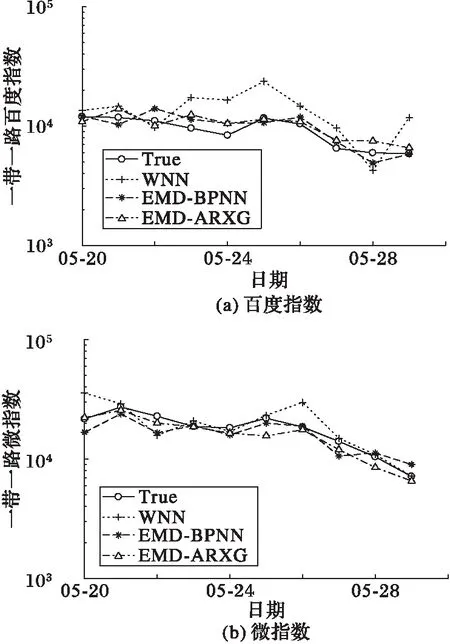
图5 2017年一带一路预测 Fig. 5 Prediction of the Belt and Road in 2017
4 结语
本文以复杂网络舆情的预测模型为研究对象,提出一种新的组合模型EMD-ARXG模型,并通过实例对比了EMD-ARXG模型与WNN和EMD-BPNN模型的预测效果。从实验结果可以看出,在RMSE、MAPE和TIC三项评价指标上,EMD-ARXG模型整体均优于WNN和EMD-BPNN模型,说明提出的EMD-ARXG模型较适合于舆情趋势的预测。综合两个领域实例的预测结果,EMD-ARXG模型均能够得到较为准确的预测值,说明此模型适合于复杂舆情的趋势预测。
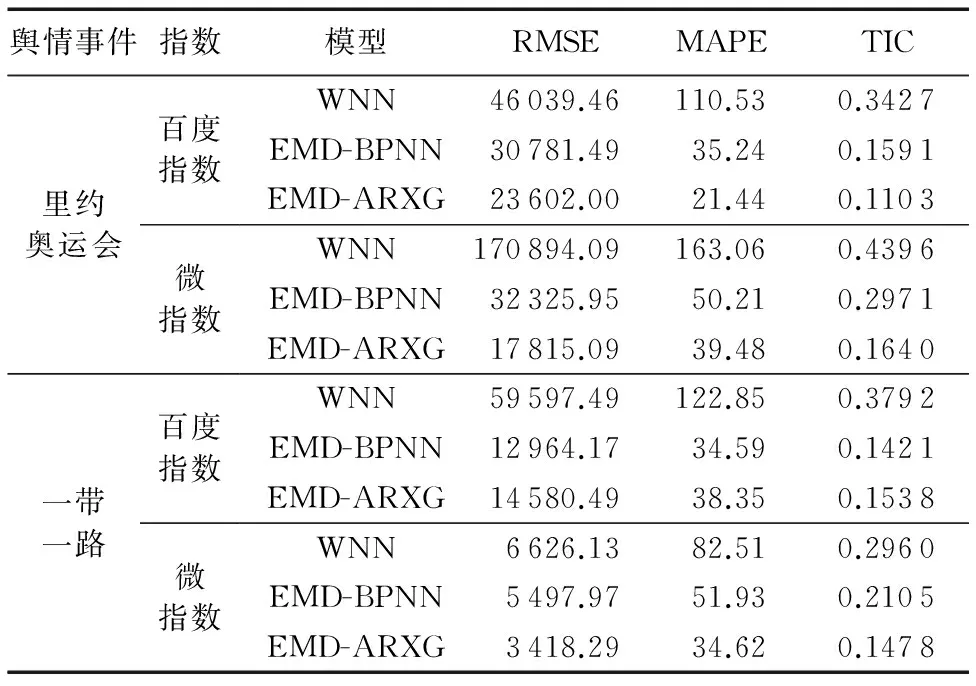
表1 三种预测模型的预测指标统计结果Tab. 1 Statistical result of prediction indexes for three prediction models
参考文献(References)
[1] CERON A, NEGRI F. The “social side” of public policy: monitoring online public opinion and its mobilization during the policy cycle [J]. Policy & Internet, 2016, 8(2): 131-147.
[2] LEEPER T J, SLOTHUUS R. Political parties, motivated reasoning, and public opinion formation [J]. Political Psychology, 2014, 35(S1): 129-156.
[3] 陈福集,李林斌.G(Galam)模型在网络舆情演化中的应用[J].计算机应用,2011,31(12):3411-3413.(CHEN F J, LI L B. Application of G (Galam) model in network public opinion evolution [J]. Journal of Computer Applications, 2011, 31(12): 3411-3413.)
[4] URBAN J, BULKOW K. Tracing public opinion online — an example of use for social network analysis in communication research [J]. Procedia — Social and Behavioral Sciences, 2013, 100(7): 108-126.
[5] 方薇,何留进,孙凯,等.采用元胞自动机的网络舆情传播模型研究[J].计算机应用,2010,30(3):751-755.(FANG W, HE L J, SUN K, et al. Study on dissemination model of network public sentiment based on cellular automata [J]. Journal of Computer Applications, 2010, 30(3): 751-755.)
[6] JAMALI S, RANGWALA H. Digging Digg: comment mining, popularity prediction, and social network analysis [C]// Proceedings of the 2009 International Conference on Web Information Systems and Mining. Washington, DC: IEEE Computer Society, 2009: 32-38.
[7] 魏超.新媒体技术发展对网络舆情信息工作的影响研究[J].图书情报工作,2014,58(1):30-34.(WEI C. Study on the impact of new media technology development on Internet public opinion information work [J]. Library and Information Service, 2014, 58(1):30-34.)
[8] 柯赟.基于动态贝叶斯网络的舆情预测模型研究[J].统计与决策,2016(20):26-28.(KE Y. Research on network public opinion prediction model based on dynamic Bayesian network [J]. Statistics and Decision, 2016(20): 26-28.)
[9] 李文杰,化存才,何伟全,等.网络舆情事件的灰色预测模型及案例分析[J].情报科学,2013(12):51-56.(LI W J, HUA C C, HE W Q, et al. Gray prediction model of network public opinion event and analysis of examples [J]. Information Science, 2013(12):51-56.)
[10] 滕文杰.时间序列分析法在突发公共卫生事件网络舆情分析中的应用研究[J].中国卫生统计,2014,31(6):1071-1073.(TENG W J. Application of time series analysis in public opinion analysis of public health emergencies [J]. Chinese Journal of Health Statistics, 2014, 31(6): 1071-1073.)
[11] CHOI B S. A recursive algorithm for solving the spatial Yule-Walker equations of causal spatial AR models [J]. Statistics & Probability Letters, 1997, 33(3): 241-251.
[12] 黄远,沈乾,刘怡君.微博舆论场:突发事件舆情演化分析的新视角[J].系统工程理论与实践,2015,35(10):2564-2572.(HUANG Y, SHEN Q, LIU Y J. Microblog public opinion field: a new perspective for analyzing evolution of emergency opinion [J]. System Engineering — Theory & Practice, 2015, 35(10): 2564-2572.)
[13] FRIEDMAN J, HASTIE T, TIBSHIRANI R. Additive logistic regression: a statistical view of boosting [J]. Annals of Statistics, 2000, 28(2): 337-374.
[14] CHEN T, GUESTRIN C. XGBoost: a scalable tree boosting system [C]// KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 785-794.
[15] ESHEL G. The Yule Walker equations for the AR coefficients [EB/OL]. [2017- 04- 01]. http://www-stat.wharton.upenn.edu/~steele/Courses/956/ResourceDetails/YWSourceFiles/YW-Eshel.pdf.
[16] 游丹丹,陈福集.基于改进粒子群和BP神经网络的网络舆情预测研究[J].情报杂志,2016,35(8):156-161.(YOU D D, CHEN F J. Research on the prediction network public opinion based on improved PSO and BP neural network [J]. Journal of Intelligence, 2016, 35(8):156-161.)
This work is partially supported by the National Natural Science Foundation of China (711710); the “Twelfth Five-Year” National Science and Technology Support Program Major Issues (2011BAD13B11); the Guangdong Provincial Regional Demonstration Project for Marine Economic Innovation and Development (GD2013-D01- 001).
MOZan, born in 1962, Ph. D., professor. His research interests include e-commerce,information management system.
ZHAOBing, born in 1993, M. S. candidate. Her research interests include machine learning, data mining.
HUANGYanying, born in 1991, M. S. candidate. Her research interests include machine learning, data mining.

