基于Golomb序列调制的目标距离速度测量方法

王瑞东，程用志，熊 莹，周兴林，毛雪松

(1.武汉科技大学 信息科学与工程学院，武汉 430081； 2.武汉科技大学 计算机科学与技术学院，武汉 430065;3.武汉科技大学 汽车与交通工程学院，武汉 430065)

0 引言

道路目标距离和速度的同步测量是无人驾驶车辆环境信息感知的重要内容，是其路径规划与智能决策的基础。对环境信息的感知包括以红外、相机等为代表的被动方式和以雷达、超声波、激光雷达等为代表的主动方式。被动方式中，立体相机[1-2]通过图像匹配可以实现对目标距离的测量，其测量精度在近距离可以达到10 cm左右，随着距离的增加，测量精度会下降。主动方式中，毫米波雷达[3-4]和激光雷达[5-6]都可以实现目标距离的精确测量，其中毫米波雷达还可以同步测量目标的速度[7]。然而，在这些方式中，通过立体相机测量目标距离受光照环境影响很大，不能全天候工作。通过毫米波雷达虽然可以全天候测量目标的距离和速度，但受限于波源振荡器辐射的脉冲宽度在微秒级，须采用连续波的信号处理方式。同时，由于波束较宽，其在道路环境中应用时存在多径干扰、串话等问题。不使用连续波而改用脉冲方式，是解决多径干扰、串话等问题的一种重要方式。半导体二极管激光器辐射的连续波通过外部光学调制器很容易实现连续波到脉冲的转换，同时脉冲之间的相干性得到保留[8]。另外激光具有良好的准直特性，使得在同一波束内出现多目标的可能性大大下降。这些都使得激光雷达成为无人驾驶车辆感知道路环境信息的一种重要的传感器。

激光雷达用于目标测量有连续波和脉冲两种方式，使用连续波则与毫米波雷达一样存在多径干扰、串话等问题，因此用于道路目标距离测量的激光雷达均使用脉冲的方式。然而，到目前为止，尚无激光雷达能够完成道路目标距离和速度的同步测量。课题组前期研究提出了基于伪随机码[9-10]、伪随机码插入周期码[11-12]等方式，从原理上可以实现目标距离和速度的同步测量。在实际应用中，受限于激光的安全标准[13]，使用1 550 nm波长光源的情况下，平均发射功率不能高于10 mW。伪随机码调制信号具有近似连续特性，其“1”码所占时隙宽度为发射信号长度的一半，因此发射信号的峰值功率被限制在一个很小的范围内，导致接收信号在一个码元宽度内的能量接近甚至低于单光子能量。在光电转换器和后续放大电路都存在噪声的实际情况下，接收信号的检测异常困难。

为了能够提高发射信号的峰值功率，就必须减少调制码中“1”码的个数，然而“1”码个数的下降会导致对激光雷达输出的外差信号采样率下降，当平均采样率低于奈奎斯特频率的情况下，快速傅里叶变换(Fast Fourier Transform, FFT)方法对外差信号频率分析时出现频谱混叠，从而不能正确计算出多普勒信号的频率，即不能正确测量目标的速度。针对上述问题，本文在前期工作[9-10]的基础上，提出了一种基于Golomb序列的脉冲式多普勒激光雷达发射信号波形调制方案，减少了发射信号中脉冲的个数从而提高发射信号的峰值功率。针对这种调制方法，通过对外差信号数据累加求取激光的飞行时间获得目标的距离；利用Golomb序列的时间间隔特性，计算外差信号相关函数获得近似等间隔序列，并对序列作FFT求取多普勒信号频率获得目标速度。

1 脉冲式多普勒激光雷达

激光雷达采用文献[9]中图1所示的双检测器结构，分别用于测量目标的距离和速度,不同的只是这里采用的调制码为服从Golomb时间分布的脉冲串，以及对应于接收端的信号处理方式。

1.1 伪随机码调制

伪随机码调制激光雷达光电转换器输出的外差信号波形如文献[10]的图2所示。通过对输出信号求与本地调制码相关函数可以确定因激光飞行带来的延迟时间，进而求出目标的距离；同时对输出信号作不等间隔采样信号频谱分析，可以求出多普勒频率，进而求出目标的速度。从原理上看，该方法可以很好地实现道路环境目标的距离和速度同步测量；但是，伪随机码的“1”码和“0”码出现的概率相等，使得发射的脉冲序列表现出近似连续的特性，即发射脉冲序列中有激光信号存在的时间占发射信号时间的一半。

根据激光安全标准[13]，为了使1 550 nm波长激光雷达工作于Class 1的安全等级，发射信号的平均功率不能高于10 mW。激光雷达发射信号的波形如图1所示。假设激光雷达测量频率达到20 000次/s，则单次测量所发射的脉冲序列长度应小于5 μs；另外假设测量的最大距离为150 m，则激光的最大飞行时间为1 μs；因此在5 μs发射信号的尾部应保留大于1μs的死区用于等待最后一个脉冲到达激光雷达接收机，故实际脉冲序列长度应小于4 μs，这里以4 μs计算。设激光雷达的扫描角度为120°，如果人站在距离激光雷达10 m距离处，则每秒内将有近1 000个脉冲串进入人眼。在这种情况下，假设允许发射的脉冲峰值功率为Pt(单位：mW)，则：

Pt×4 μs×(1/2)×1 000=10 mW

(1)

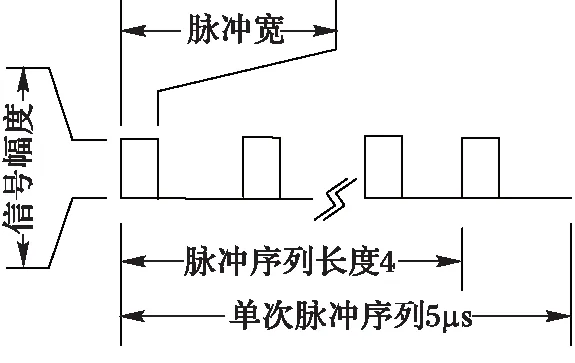
图1 激光雷达发射的伪随机脉冲序列结构 Fig. 1 Pseudo-random pulse sequence structure of laser radar emission

因此发射脉冲的峰值功率将不超过5 W。根据雷达方程[14]，可以近似估算出激光雷达接收到的脉冲信号功率。假设激光光斑全部照射在目标上，接收回波的光学镜头半径为1 cm，目标的反射率为10%，不考虑大气损耗和光学透镜的吸收，则接收到的回波峰值功率为2.5 nW。为了提高激光雷达距离测量精度，发射的脉冲宽度通常很窄，已有激光雷达发射皮秒级脉冲，这里假设脉冲宽度为1 ns，则一个比特符号内接收到的光子能量为2.5×10-18J。

根据物理学的知识，1 550 nm波长单光子的能量(单位：J)为：

(2)

可见，伪随机码调制激光雷达所能接收到的光子在一个比特时间内以个数计算，这对于使用PIN光电二极管的激光雷达来说，信号的检测非常困难。在实际的激光雷达中，还必须考虑上述未考虑的光学损耗、发射镜头与接收镜头之间的校准损耗、激光雷达内部光路中的光学损耗等各种因素，因此，使用伪随机码调制的方法，不可能实现一个性能稳定且体积小的激光雷达。为了提高回波信号功率，必然增大接收端镜头尺寸，从而在车辆上安装时消耗更多的汽车表面面积。

1.2 Golomb序列调制

从数学上看，Golomb序列就是一组整数，每两个整数构成一个整数对，整数对之间的间隔都互不相等。例如，{0 1 4 6}构成一个Golomb序列，其间隔如图2所示。

定义Golomb序列中元素的个数为阶，最大数为其长度，则图2给出的是长度为6的4阶Golomb序列。从图中可以看出这种序列之间的间隔互不相等，而且间隔从1以等差方式递增到6。如果将激光雷达的发射脉冲时间间隔以Golomb序列间隔的方式分布，则可以利用上述特性减少发射脉冲的个数，在同等平均发射功率的情况下提高单个脉冲的峰值功率。图2中序列的长度与阶数差距不大，相比伪随机码并不能看出其优越性，实际上可以通过使用计算机算法构造出阶数低、长度大的Golomb序列[15-16]，从而可以极大提高发射脉冲的峰值功率。

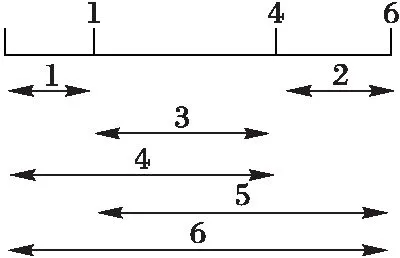
图2 长为6的4阶Golomb序列 Fig. 2 A 4th-order Golomb series with a length of 6

2 Golomb序列调制信号频谱分析

将发射光脉冲的时间间隔按照Golomb序列的方式分布，激光雷达输出的信号则为幅度受多普勒频率调制、间隔按Golomb序列方式分布的非等间隔脉冲串。对输出信号采样，不能得到多普勒信号的等间隔采样数据，因此不能使用FFT算法对采样信号作频谱分析工作。

从图2可以看到，Golomb序列整数对之间的间隔从1按等差的方式增加到序列的长度，如果按照式(3)计算这种序列的自相关函数：

(3)

其中：x(n)为间隔服从Golomb序列分布的时间信号，q(n)为间隔为n的整数对的个数，则虽然时间序列本身的数据是非等间隔的，但得到的自相关函数的数据为等间隔分布，如图3所示。

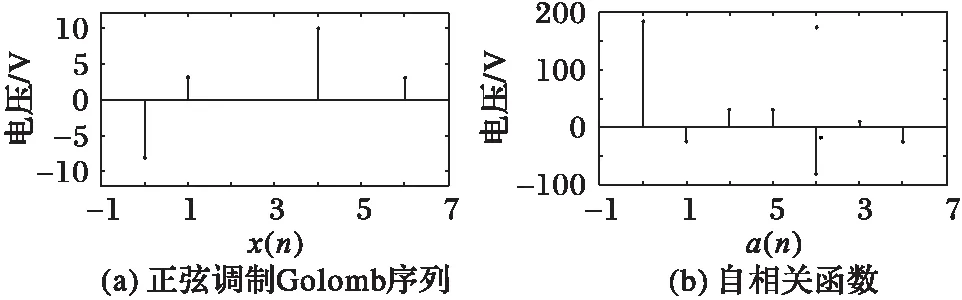
图3 Golomb序列及其自相关函数 Fig. 3 Golomb series and its self-correlation function

很显然，序列本身在0～6的间隔并不相等，但其自相关函数具有相等的时间间隔。

我们知道，自相关函数的傅里叶变换是信号的功率谱S(ω)；另一方面，功率谱是信号傅里叶变换幅度谱X(ω)的平方，即：

S(ω)=|X(ω)|2

(4)

因此，在不需要知道信号相位谱的情况下，完全可以利用自相关函数的傅里叶变换来代替信号本身的傅里叶变换，求取信号的频率。

3 数据累加

数据累加是一种提高接收信号信噪比的经典方法[14]，雷达发送等间隔的脉冲序列，在接收端从各自脉冲发射开始时刻采样相同时间长度的数据，并将数据相加。由于信号在采样数据中相位相同，而噪声相位随机，因此相加后的信噪比得到提高。假设发射脉冲串中包含N个脉冲，则通过数据累加得到的信号信噪比可以提高10 lgN。这种经典方法必须在前一个脉冲的反射回波被接收到后，才可以发射后一个脉冲，因此测量速度被极大限制。

本文提出按Golomb序列分布的脉冲串调制发射信号波形，激光雷达无需等待前一个脉冲的回波，只需按照序列本身规定的时间间隔发射即可。到目前为止，Golomb序列的时间间隔是正规化后的整数，对应到道路环境感知激光雷达，可以将整数映射到具体的时间单位，即将序列的长度映射到图1中的4 μs，起始位置映射到0，其他脉冲均按比例对应到时间轴上。接收端从第一个脉冲发射时刻起采样一段长为5 μs的数据，这段数据包含所有脉冲的回波，将这段数据记为s0(t)，它表现为发射脉冲串经一段时间延迟并在幅度上衰减，如图4第1行所示。

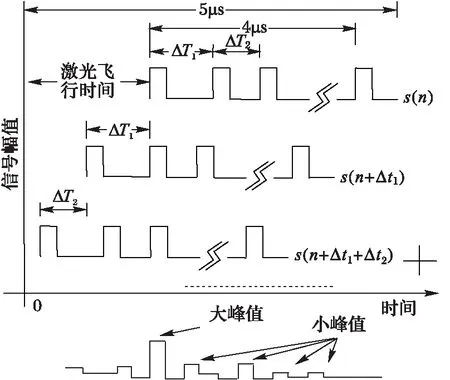
图4 Golomb序列的数据累加方法 Fig. 4 Data accumulation method for Golomb series

在发射端生成Golomb脉冲串时，需要保存脉冲之间的间隔，这些间隔分别记为ΔT1、ΔT2、…、ΔTN-1，N为脉冲的个数。将s0(t)向左平移ΔT1并记为s1(t)，将s1(t)向左平移ΔT2并记为s2(t)，按这种方式重复直到将sN-2(t)向左平移ΔTN-1并记为sN-1(t)，将平移后得到的数据分别放置于图4的第2行、第3行、…、第N行并将所有行相加。只有在对应于飞行时间延迟的时刻各行都有一个脉冲，因此相加后该位置得到的数值最大，而其他位置由于脉冲之间的间隔不相等，因此仅出现一些很小的峰。在考虑接收机噪声的情况下，这些小峰值淹没在噪声中。

4 仿真结果与分析

选用1 550 nm波长作为辐射光源，当目标速度在1 m/s(对应于人步行速度)到100 m/s(两车均以180 km/h相对运动)范围内，由于运动所产生的多普勒频率范围为1.29～129 MHz。前面提到序列的时间长度应小于4 μs，另一方面为了使序列能够覆盖低频信号的一个周期，序列长度应大于775 ns。仿真中选用的Golomb序列为{ 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372}，其长度为372，阶数为23。在Golomb序列的末位补16个0，并使用宽度为2 ns的脉冲，则时间窗口长度刚好覆盖1.29 MHz信号的一个周期。同样可以使用补0的方式将发射脉冲串长度延长到4 μs，但这种补0的过程对仿真不产生影响，故这里不计入。如果使用伪随机码调制，长度为372，则应有186个脉冲，而使用Golomb序列，则脉冲的个数仅为23，因此脉冲数量得到极大的压缩，可允许的发射功率可以增加近10倍。如果选用更长的Golomb序列，可以进一步压缩脉冲个数与发射信号长度的比。

设接收到的信号幅度为0.1，噪声功率为0.01，即信噪比为0 dB时，回波信号被完全淹没在噪声中，如图5(a)所示。对淹没在噪声中的信号执行图4所示的数据累加算法，得到如图5(b)所示结果。与图4的理论分析一致，对应于因激光飞行时间的位置有一个很大的峰值，其他小峰都被淹没在噪声中。

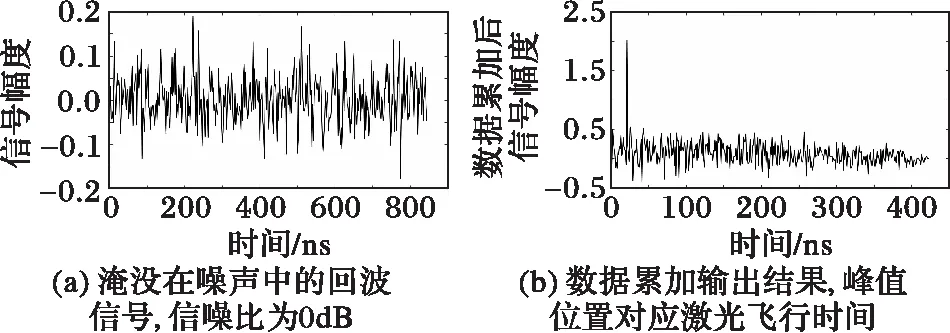
图5 回波分析结果 Fig. 5 Echo wave analysis results

对外差检测光电转换器输出的信号按式(3)先作相关运算，然后对相关运算的结果作FFT运算。类似于文献[12]，选择1.29、5、10、20、50、129 MHz这6个频率，计算结果如图6所示。对多普勒信号的初始相位在[0，2π]内随机改变，可以观察到图6所示的相关谱峰值几乎不受影响，因此这种方法对于计算单频多普勒信号是有效的。

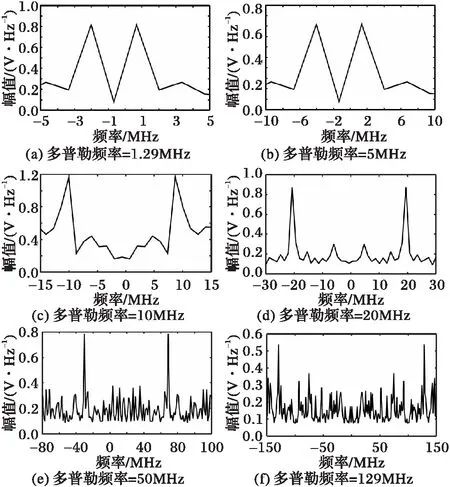
图6 多普勒信号频谱分析结果 Fig. 6 Spectrum analysis results of Doppler signal

从图6中还可以看出，计算得到的频率中心偏离原点，因此正频率和负频率不相等。可通过求平均的方式来减小误差。图6中6个频谱的正负频率如表1所示，计算平均后得到的频率与实际频率的误差控制在1 MHz范围内，这是由仿真中所使用的采样频率、采样点数所决定的。对1.29 MHz的低频信号作多次仿真，其误差都在0.1 MHz附近。综合仿真结果，通过求相关频谱的方法得到的频率与实际多普勒频率的相对误差都小于0.1，在对道路目标测速应用中属于允许范围内。

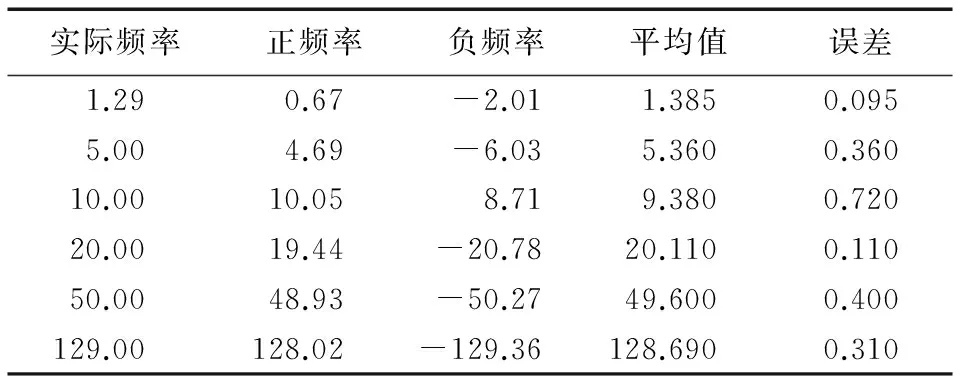
表1 图6对应的正负频率及其平均值 MHzTab. 1 Positive/Negative frequencies corresponding to those in Fig. 6, and their averages MHz

5 结语

激光雷达在道路环境信息感知的应用中，目前只能测量目标的距离，而不能测量目标的速度。前期工作提出的伪随机码调制方法从理论上可以实现激光雷达距离和速度同步测量，但存在发射脉冲峰值功率低、接收回波信号接近光子极限的问题。本文提出一种基于Golomb序列的发射信号波形方法，利用Golomb序列间隔的特定关系，在接收端对回波信号分析时，通过数据累加方法计算回波的延迟时间，提高激光雷达接收灵敏度，通过先计算回波的相关函数使基于Golomb序列的不等间隔数据均匀化，再通过计算相关函数的傅里叶变换求出回波信号中的多普勒频率。相比前期提出的伪随机码方法，Golomb序列调制方式使用的脉冲个数少，因此在平均功率不变的情况下，可以提高脉冲的峰值功率。最后，在由23个2 ns脉冲构成4 μs发射信号长度，且接收信号信噪比达0 dB的情况下，使用计算机仿真验证了数据累加方法确定信号延迟的可行性；在接收信号的多普勒频率为1.29～129 MHz范围内，选取6个频率点，验证了通过自相关求频谱的有效性，验证了方法与接收信号初始相位的无关性。本文结果表明，通过使用Golomb序列调制激光雷达发射信号波形，可以在保持平均功率不变的情况下，提高发射脉冲的峰值功率，增强激光雷达对目标的探测灵敏度，同时具有对目标距离和速度同步测量的功能。

参考文献(References)

[1] MAHAMMED M A, MELHUM A I, KOCHERY F A. Object distance measurement by stereo vision [J]. International Journal of Science and Applied Information Technology, 2013, 2(2): 5-8.

[2] WU B, YE L, YANG Y. Accuracy analysis of a dual camera system with an asymmetric photogrammetric configuration [J]. Photogrammetric Engineering & Remote Sensing, 2015, 81(3): 219-228.

[3] LI C, PENG Z, HUANG T, et al. A review on recent progress of portable short-range noncontact microwave radar systems [J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(5): 1692 -1706.

[4] PATOLE S M, TORLAK M, WANG D, et al. Automotive radars: a review of signal processing techniques [J]. IEEE Signal Processing Magazine, 2017, 34(2): 22-35.

[5] BUTERA S, VINES P, TAN C H, et al. Picosecond laser ranging at wavelengths up to 2.4 μm using an InAs avalanche photodiode [J]. Electronics Letters, 2016, 52(5): 385-386.

[6] 杨宏志,赵长明,张海洋,等.全光纤激光雷达发射和接收光学系统设计与优化[J].光学学报,2016,36(11):58-65. (YANG H Z, ZHAO C M, ZHANG H M, et al. Design and optimization of all-fiber lidar transmitting and receiving optical systems [J]. Acta Optica Sinica, 2016, 36(11): 58-65.)

[7] LEE T-Y, JEON S-Y, HAN J, et al. A simplified technique for distance and velocity measurements of multiple moving objects using a linear frequency modulated signal [J]. IEEE Sensors Journal, 2016, 16(15): 5912-5920.

[8] KHWANDAH S A, COSMAS J P, GLOVER I A, et al. Direct and external intensity modulation in OFDM RoF links [J]. IEEE Photonics Journal, 2015, 7(4): 1-10.

[9] 方建超,毛雪松.非等间隔采样信号傅里叶频谱分析方法[J].计算机应用,2016,36(2):492-494,504. (FANG J C, MAO X S. Fourier spectrum analysis for non-uniform sampled signals [J]. Journal of Computer Applications, 2016, 36(2): 492-494, 504.)

[10] 郑刚,程用志,毛雪松. 基于伪随机码调制的车载激光雷达距离速度同步测量方法[J].计算机应用,2017,37(3):911-914.(ZHENG G, CHENG Y Z, MAO X S. Simultaneous range and speed measurement by vehicle laser radar based on pseudo-random noise code modulation [J].Journal of Computer Applications, 2017, 37(3): 911-914.)

[11] MAO X, INOUE D, KATO S, et al. Amplitude-modulated laser radar for range and speed measurement in car applications [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 408-413.

[12] MAO X, INOUE D, MATSUBARA H, et al. Demonstration of in-car Doppler laser radar at 1.55 μm for range and speed measurement [J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 599-607.

[13] Microelectronics Group, Lucent Technologies, Bell Labs Innovations. Laser safety and optical-fiber communication systems [EB/OL]. [2017- 04- 06]. https://r.search.yahoo.com/_ylt=AwrXnY_7enlaIiAAMEJXNyoA;_ylu=X3oDMTExbDBrcXNoBGNvbG8DZ3ExBHBvcwMzBHZ0aWQDVUlDMV8xBHNlYwNzcg--/RV=2/RE=1517939580/RO=10/RU=http%3a%2f%2farchive.eetasia.com%2fwww.eetasia.com%2fARTICLES%2f1999DEC%2f1999DEC28_AMD_NTEK_PM_AN.PDF%3fSOURCES%3dDOWNLOAD/RK=2/RS=_70nZ18qaXwFwriA.ROr8cUbIJU-.

[14] RICHARD M A. Fundamentals of Radar Signal Processing [M]. 2nd ed. New York: McGraw-Hill Higher Education, 2014:42-44.

[15] BREJZA M F, WANG T, ZHANG W, et al. Exponential Golomb and Rice error correction codes for generalized near-capacity joint source and channel coding [J]. IEEE Access, 2016, 4: 7154-7175.

[16] SORGE M, MOSER H, NIEDERMEIER R, et al. Exploiting a hypergraph model for finding Golomb rulers [J]. Acta Informatica, 2014, 51(7): 449-471.

[17] BANSAL S. Optimal Golomb ruler sequence generation for FWM crosstalk elimination: soft computing verse conventional approaches [J]. Applied Soft Computing, 2014, 22: 443-457.

This work is partially supported by the National Natural Science Foundation of China (61605147).

WANGRuidong, born in 1992, M. S. candidate. His research interests include road environment sensing.

CHENGYongzhi, born in 1984, Ph. D., associate professor. His research interests include optic and electromagnetic metamaterial.

XIONGYing, born in 1978, M. S., engineer. Her research interests include optical ROADM (Reconfigurable Optical Add/Drop Multiplexer) network, Internet of vehicles.

ZHOUXinglin, born in 1965, Ph. D., professor. His research interests include sensors and systems.

MAOXuesong, born in 1975, Ph. D., professor. His research interests include road environment sensing, path planning for smart vehicles, multi-mode optical devices.