结合结构自相似性和卷积网络的单幅图像超分辨率

向 文，张 灵，陈云华，姬秋敏

(广东工业大学 计算机学院，广州 511400)

超分辨率(Super Resolution, SR)图像重建是指对低质量、低分辨率(Low-Resolution, LR)图像进行处理,恢复出高分辨率(High-Resolution, HR)图像的技术,在军事、医学、公共安全、计算机视觉等方面都存在着广泛的应用前景。超分图像重建的一种方法是采用大量高分辨率图像学习,以得到图像的高频细节对低分辨率图像进行恢复[1-4]。目前算法多依赖训练数据库数据,没有充分利用待重构图片自身的结构特点,造成重构效果不佳[5-7]。Freedman等[8]指出在单幅图像的局部空间邻域内存在大量结构自相似的图像块，因而提出了一些利用局部结构自相似性方法[9-10]，但是这些算法不能有效处理没有重复结构的不规则纹理图像块，图像块间的错误匹配会带来很多虚假纹理,重构效果难以保证。鉴于目前存在的问题，本文提出了一个基于待重构图像的结构相似性特征和卷积神经网络(Convolution Neural Network, CNN)相结合的超分图像重构方法,从单幅低分辨率图像中获取自身结构在相同尺度和不同尺度下的结构冗余信息,并结合深度学习方法进行超分辨率重建。首先提取单幅图像在相同及不同尺度下的重复出现结构特征；然后融合高分辨率字典图像块输入到CNN中进行学习,从而实现单幅低分辨率图像的重构,实验结果验证了本文算法的有效性。

1 卷积神经网络模型

近年来,深度学习在许多计算机视觉图像问题上取得了很大的成功,说明了神经网络模型在学习数据集本质特征上具有强大的能力。有研究学者提出了基于卷积神经网络的图像超分辨率(Super-Resolution Convolution Neural Network, SRCNN)方法[11]，利用外部数据库中成对的LR和HR图像，通过CNN模型获得相应的先验信息，来实现超分辨率重建。超分辨率卷积神经网络由三层卷积层构成，分别为特征提取、非线性映射和高分辨率图像重构，该算法框架如图1所示。SRCNN的深度学习网络中的三个卷积网络公式表达如下:

Y1=max(0,W1*X+B1)

(1)

Y2=max(0,W2*Y1+B2)

(2)

Y3=max(0,W3*Y2+B3)

(3)

其中：矩阵X代表LR子图像；Yi(i=1,2,3) 表示每个卷积层的输出；Wi(i=1,2,3)和Bi(i=1,2,3)分别代表神经元卷积核和神经元偏置向量；*表示卷积运算，卷积得到的特征图要再经ReLU激活函数max(0,x)进行处理。在训练过程,该神经网络需要学习参数Θ={W1,W2,W3,B1,B2,B3}，该参数通过最小化神经网络输出与HR图像之间的误差损失进行训练估计。给定高分辨率图像Yi与其相应的低分辨率图像集合Xi，用其均方误差L(Θ)作为驱动损失函数：

(4)

式(4)可通过随机梯度下降和反向传播算法进行训练求解。

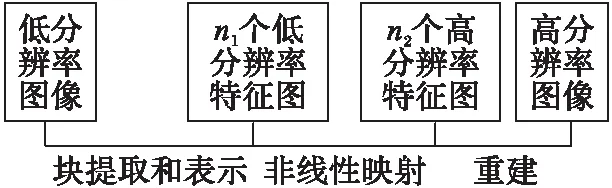
图1 SRCNN 算法框架 Fig. 1 Structure of SRCNN algorithm

2 结构自相似性理论

2.1 图像的多尺度自相似

在整幅图像的各个区域之间普遍存在的相似特性统称为图像相似性。有研究[12]表明,对于自然图像中一个5×5的图像块,在该图像中能发现大量与其相似的相同尺度和不同尺度的图像块。统计表明,超过90%的图像块能找到至少9个相同尺度的相似图像块；超过80%的图像块能找到至少9个不同尺度的相似图像块。根据这种图像相似性,可以在相同尺度和不同尺度上提取出图像自身的很多冗余信息。Candocia等[13]指出一般的图像具有如下两个特点：整幅图像中存在着大量具有相似结构的区域;并且这些结构的相似性在多个尺度上可以保持。

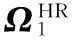
在本文中采用非局部块匹配的方法对外部数据库在相同尺度和不同尺度上搜寻相似图像块,组成具有多尺度结构自相似性的LR和HR图像块对,将这种LR和HR图像块对作为训练样本字典。另外对内部数据库采取同样的方法在多尺度上搜索相似高分辨率图像块作为内部高分辨率字典。

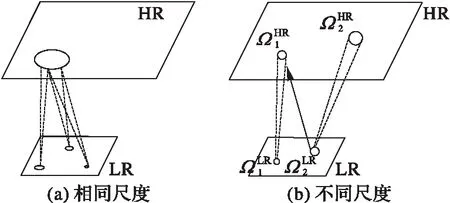
图2 在相同尺度和不同尺度相似图像块的SR方法 Fig. 2 SR method of similar image blocks on same scale and difierent scales

2.2 非局部自相似性约束

由于非局部图像块之间可以提供额外的有用信息，因此利用不同区域图像块之间的相似性似乎能够获得更高的图像分辨率[14]。它们首先将训练图像分成大小相同的图像块，然后经过将高、低分辨率图像块进行配对形成字典，最后在字典中寻找与低超分辨率图像块相似的若干图像块，将全部选中的图像块加权整合得到近似的高分辨率图像块，接着将全部的近似高分辨率图像块融合得到全部的高分辨率结果图像。学者们经过研究分析提出[15-16]：一方面，自然图像在其纹理、物体边缘等区域存在丰富的相似性，低分辨率图像可以根据该相似性重建出丢失的高频细节；另一方面，高、低分辨率图像之间具有近邻保持关系。

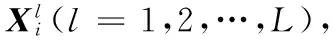
(5)

其中：I为单位矩阵，B为权值矩阵，ψ为字典矩阵。

3 基于结构自相似性的神经网络算法

3.1 低分辨率降质模型

LR图像是由HR图像经过模糊、降采样以及噪声污染得到的[17]，整个降质过程近似地表示为一个线性过程，那么图像降质模型可以表示为：

X=HSY+n

(6)

其中：H是下采样操作，S是模糊算子，n是噪声污染矩阵。SR问题就是已知给定的单幅LR图像矩阵X,重建出相同场景中的HR图像矩阵Y。为了准确估计出HR图像矩阵Y,需要引入图像的一些先验或正则约束项：

(7)

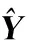
(8)

其中μ为正则化参数，最后使用迭代反投影算法对图像进一步提升。

3.2 算法实现

先利用原始低分辨率图像的非局部自相似性提供先验知识,用多尺度的方法搜索到初始超分辨率图像块的最佳匹配块，作为内部字典，进行非局部的方法学习得到非局部正则化约束项。深度学习普遍从大数据训练，使用了一个由91张图像组成的小型训练集[3]，将此数据库用多尺度的方法进行搜索得到图片的最佳匹配块与低分辨率图像块形成高低分辨率块对，作为外部字典，输入到卷积神经网络进行训练得到卷积神经网络模型参数；然后再用卷积神经网络模型参数对原始低分辨率图像进行重建，防止伪影加入由内部数据库得到的非局部正则化约束项。该算法分为4个部分：初始插值、非局部块匹配、神经网络模型学习和非局部正则化约束。

1)初始插值：本文选取现有比较常用且重建视觉效果较好的三次双线性插值算法得到初始超分辨率图像，插值算法的选取对最终超分辨率结果产生一定的影响，较好的插值算法必然会得到较好的最终结果。

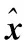
(9)

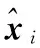
3)神经网络模型学习：卷积神经网络模型具有很强的特征学习能力，在这里采用SRCNN算法中三层卷积神经网络模型对高低分辨率图像块进行学习。将块匹配得到的高低分辨率图像块对输入超分辨率卷积神经网络，经过三层卷积层, 通过特征提取、非线性映射，最终得到需要的超分变辨率图像参数模型Θ。

4)非局部正则化约束：这部分结合卷积神经网络模型，非局部正则化参数和字典等参数根据式(8)进行计算，得到重建的超分辨率图像。

3.3 算法优化

使用迭代反投影算法对重建的图片进行提升,该方法采用下采样子像素位移图像降质模型[18]采样获得多帧LR图像，将其配准, 最后通过对模拟LR图像和观测LR图像的误差进行迭代反投影到HR图像。假设输入K幅观测LR序列图像为fk(m1;m2),分辨率为M1×M2,估计的HR图像f(n1;n2)扩大了l倍，则(N1;N2)= (lM1)×(lM2)。用迭代反投影(Iterative Back Projection, IBP)方法对HR图像进行估计,公式可表示为：

(10)

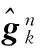
3.4 算法流程

本文提出的结构自相似性结构神经网络算法分为两个阶段,分别为训练阶段和重建阶段，具体步骤如下。

3.4.1 训练过程

步骤1 输入外部数据库，将其缩小至原来的1/3，获得低分辨率图像，将其进行插值放大得到初始高分辨率图像。

步骤2 将外部数据库中的初始高分辨率图像和低分辨率图像划分成3×3的小块。

步骤3 取块，在相同尺度和不同尺度下用非局部块匹配搜索的方法，利用式(9)找到最匹配的块组，再用加权平均的方法求出最匹配块。

步骤4 将匹配块和一一对应的低分辨率块组成具有结构自相似性的LR和HR图像块对，作为外部训练样本字典。

步骤5 将具有结构自相似性的外部数据库LR和HR图像对作为训练库输入卷积神经网络。

步骤6 利用式(4)学习LR到HR图像的映射函数，得到训练参数集Θ={W1,W2,W3,B1,B2,B3}。

3.4.2 重建过程

步骤1 利用双三次插值将输入单幅LR图像放大到和HR图像大小一样,作为初始重建图像X0。

步骤2 将初始重建图像X0用多尺度非局部正则化方法提取内部字典和非局部正则化约束参数矩阵。

步骤3 利用式(8)将外部训练样本字典作为输入，正则化约束参数矩阵作为初始训练参数通过卷积神经网络学习得到卷积神经网络模型参数。

步骤4 利用内部字典和卷积神经网络模型参数重建目标图像。

步骤5 采用迭代反投影算法对目标图像进一步提升重建效果。

3.5 算法示例

为了更加清晰、明确地说明本文算法，给出算法流程如图3所示。

经过卷积神经网络的过程是一种端对端映射的过程，可以用图4的简单示例来表示。图4中的过程由箭头指引分别为：输入、第一层的特征图、第二层的特征图和输出。

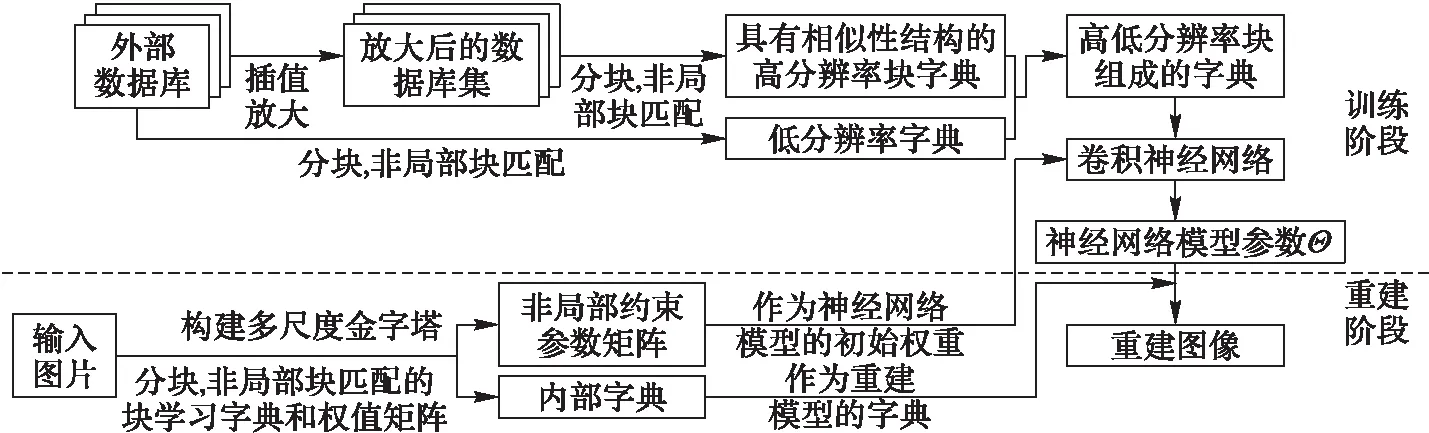
图3 本文算法流程 Fig. 3 Flow chart of the proposed algorithm

图4 卷积神经网络的示例 Fig. 4 Examples of CNN

4 实验结果与分析

4.1 实验设置

为了验证所提方法的有效性，选取3个国际公开的SR数据库：Set5、Set14和Urban100，并在三种常用放大因子(2、3和4)情况下进行实验验证。实验中采用三层卷积神经网络进行学习,利用式(1)～(3)学习得到神经网络模型，第1层的卷积核和神经元个数为9×9和64，第2层的卷积核和神经元个数为1×1和32，第3层的卷积核和神经元个数为5×5和1，本文训练次数为5万次。实验中以双三次插值(Bicubic)方法作为基准对比方法，并选择K-SVD(Singular Value Decomposition)、卷积神经网络作为对比实验，以检验本方法的性能。利用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)评价不同图像SR方法的性能。

4.2 实验结果对比

通过实验结果来验证本方法的有效性。为了评价图像重建的质量，同时从主观视觉和客观评价两个方面衡量对比结果。以数据库Set14中的斑马图像为例，图5为放大3倍情况下，不同方法的主观视觉图和相应峰值信噪比。

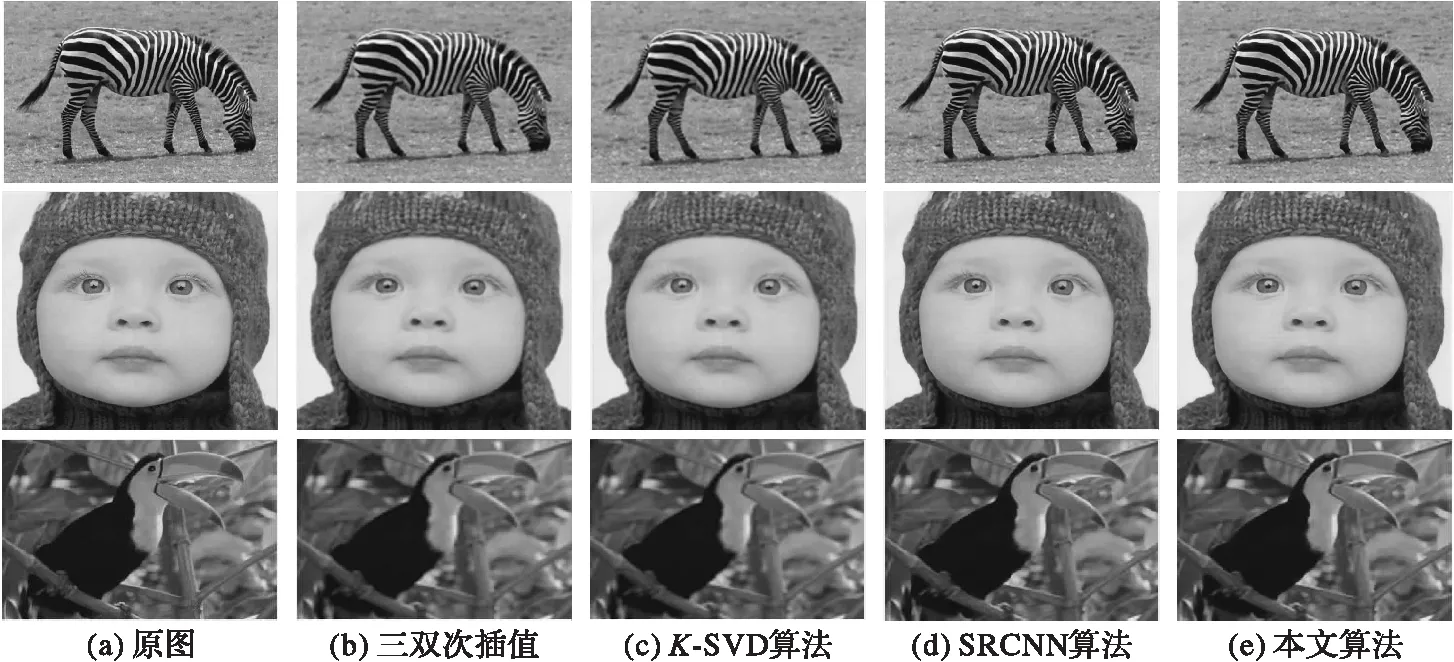
图5 四种对比算法的图像重建结果比较 Fig. 5 Image reconstruction comparison of four algorithms

主观上，可以看出本文算法的视觉效果最好，优于现有方法中的CNN方法和K-SVD。其他对比方法，在重构的图像边缘处容易产生伪影和振铃效应，一些细节没有较好地恢复出来。本文算法恢复的局部细节信息清晰细腻，整体效果更接近原始图像。由于本文算法考虑了内在图像块自相似特性，因此恢复的视觉效果最好,产生的边缘也更清晰。客观指标评价上，同样以斑马图像(zebra)为例，在放大3倍的情况下，如表1：双三次插值方法的峰值信噪比最低，只有26.633 dB；最好的对比算法只有28.867 dB左右；而本文算法在峰值信噪比上是最好的，能够达到28.937 dB。

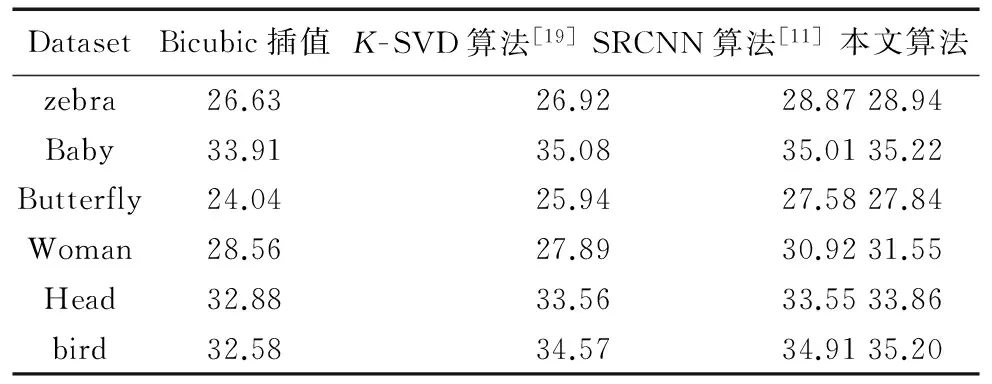
表1 不同SR方法的平均峰值信噪比对比 dBTab. 1 Average PSNR comparison of different SR methods dB

5 结语

本文算法从深度卷积网络的角度来考虑单幅图像的超分辨率问题，提出了一种基于结构相似性和卷积神经网络的单幅图像超分辨率重建算法。该算法通过图像的尺度分解获得自身结构相似性的训练样本，充分利用了输入图像自身具有的结构自相似性，解决了训练样本过于分散的问题。训练样本通过内在数据库和外部数据库相结合的方法，充分考虑了训练得到的先验知识和图像内在的结构自相似性。训练过程中的先验知识通过卷积神经网络的端对端的非线性映射得到，图像内在的结构自相似性通过非局部正则化约束项得到。最后采用迭代反投影算法进一步优化重建效果。本文算法与Bicubic、K-SVD和SRCNN等经典算法相比，可以得到更好的超分辨率重建效果。

参考文献(References)

[1] LI Z, HE H, WANG R, et al. Single image super-resolution via directional group sparsity and directional features [J]. IEEE Transactions on Image Processing, 2015, 24(9): 2874-2888.

[2] DONG C, LOY C C, HE K, et al. Image super-resolution using deep convolutional networks [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307.

[3] YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via spare representation [J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[4] TIMOFTE R, de SMET V, van GOOL L. Anchored neighborhood regression for fast example-based super-resolution [C]// ICCV ’13: Proceedings of the 2013 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2013: 1920-1927.

[5] TIMOFTE R, de SMET V, GOOL L. A+: adjusted anchored neighborhood regression for fast super resolution [C]// ACCV 2014: Proceedings of the 2014 Asian Conference on Computer Vision, LNCS 9006. Berlin: Springer-Verlag, 2014: 111-126.

[6] YANG C Y, YANG M H. Fast direct super-resolution by simple functions [C]// ICCV ’13: Proceedings of the 2013 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2013: 561-568.

[7] DAI D, TIMOFTE R, van GOOL L. Jointly optimized regressors for image super-resolution [J]. Computer Graphics Forum, 2015, 34(2): 95-104.

[8] FREEDMAN G, FATTAL R. Image and video upscaling from local self-examples [J]. ACM Translations on Graphics, 2011, 30(2): Article No. 12.

[9] PROTTER M, ELAD M, TAKEDA H, et al. Generalizing the nonlocal-means to super-resolution reconstruction [J]. IEEE Transactions on Image Processing, 2009, 18(1): 36-51.

[10] MAIRAL J, BACH F, PONCE J, et al. Non-local sparse models for image restoration [C]// ICCV ’09: Proceedings of the 2009 IEEE 12th International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2009: 2272-2279.

[11] DONG C, LOY C C, HE K, et al. Learning a deep convolutional network for image super resolution [C]// ECCV 2014: Proceedings of the 2014 European Conference on Computer Vision, LNCS 8692. Berlin: Springer-Verlag, 2014: 184-199.

[12] GKASNER D, BAGON S, IRANI M. Super-resolution from a single image [C]// ICCV ’09: Proceedings of the 2009 IEEE 12th International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2009: 349-356.

[13] CANDOCIA F M, PRINCIPE J C. Super-resolution of images based on local correlations [J]. IEEE Transactions on Neural Networks, 1999, 10(2): 372-380.

[14] DONG W, ZHANG L, SHI G, et al. Nonlocally centralized sparse representation for image restoration [J]. IEEE Transactions on Image Processing, 2013, 22(4): 1620-1630.

[15] YOU X, XUE W, LEI J, et al.Single image super-resolution with non-local balanced low-rank matrix restoration [C]// ICPR 2016: Proceedings of the 2016 23rd International Conference on Pattern Recognition. Washington, DC: IEEE Computer Society, 2016: 1255-1260.

[16] XU J, ZHANG L, ZUO W, et al. Patch group based nonlocal self-similarity prior learning for image denoising [C]// ICCV ’15: Proceedings of the 2015 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2015: 244-252.

[17] TEKALP A M, OZKAN M K, SEZAN M I. High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration [C]// ICASSP ’92: Proceedings of the 1992 IEEE International Conference on Acoustics, Speech and Signal Processing. Washington, DC: IEEE Computer Society, 1992: 169-172.

[18] LU Y, IMANURA M. Pyramid-based super-resolution of the undersampled and subpixel shifted image sequence [J]. International Journal on Systems Technology, 2002, 12(6): 254-263.

[19] AHARON M, ELAD M, BRUCKSTEIN A.K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

This work is partially supported by the Guangdong Natural Science Foundation Doctoral Program (2014A030310169), the Natural Science Foundation Project of Guangdong Province (2016A030313703, 2016A030313713), the Science and Technology Project of Guangdong Province (2016B030305002), the Science and Technology Project of Guangdong Department of Transportation (Sci. and Tech.- 2016- 02- 030).

XIANGWen, born in 1993, M. S. candidate. His research interests include image processing, pattern recognition.

ZHANGLing, born in 1968, Ph. D., professor. Her research interests include data mining, computer vision, wireless sensor.

CHENYunhua, born in 1977, Ph. D., lecturer. Her research interests include computer vision, pattern recognition, deep learning.

JIqiumin, born in 1992, M. S. candidate. Her research interests include image processing, pattern recognition.