自适应软件动态过程时间特性建模与验证方法
韩德帅,邢建春,杨启亮,2,李决龙
(1.陆军工程大学 国防工程学院,南京 210007; 2.清华大学 土木工程系,北京 100084;3.海军海防工程研究中心,北京 100841)
0 引言
自适应软件(self-adaptive software)能够在运行时实时监测上下文变化并对自身进行动态调整,以消除或减轻变化带来的不利影响。它能够有效应对运行环境和用户需求的频繁变化,降低软件维护压力,增强自身容错和应对变化的能力,现已成为软件工程领域的热点研究问题[1-4]。
为提高自适应软件的可靠性,需对自适应软件的动态过程进行形式化建模和分析。基于此,国内外学者针对自适应软件的形式化方法开展了大量研究[5-7],能够较好地支持自适应逻辑和自适应行为的刻画和分析,却鲜有研究考虑自适应动态过程的时间约束。然而,实践表明,在时间攸关应用领域,自适应软件系统能否正确运行,不仅依赖于自适应逻辑的正确性,而且要考虑系统自适应过程的时间特性。首先,自适应软件的开发需在原应用逻辑之上构建自适应逻辑,而自适应逻辑的引入势必会给原系统带来时间开销,将自适应逻辑的时间开销降到最低需综合考虑自适应各个子过程(如监控、分析、规划和执行等)的时间约束;其次,自适应软件的很多应用场景具有及时响应性,如课题组前期研究中的自适应火灾应急响应系统[8],需要系统能够及时捕获险情、及时传递险情并能够及时启动应急设备,要刻画这类具有实时性的自适应场景,时间特性是一个重要方面;最后,软件形式化方法只能分析和验证自适应逻辑的正确性,不能衡量自适应逻辑的响应速度和响应效果,现有研究尚缺乏性能指标和评估方法以全面评估自适应逻辑的性能。
基于此,本文提出一种自适应软件动态过程时间特性建模与验证方法。首先,本文显式定义了监控周期、延迟触发时间、自适应过程截止时间等时间特性用以刻画自适应动态过程各子过程的时间约束,并定义了自适应调节时间和自适应稳定时间用以定量评估自适应逻辑的响应速度和响应效果;更进一步地,本文基于时间自动机网络构建了自适应软件动态过程时间特性建模模板,实现了自适应软件时间特性的显式刻画和建模方法的复用;最后,本文将自适应软件时间特性描述为定时计算树逻辑(Timed Computation Tree Logic, TCTL)形式,并借助模型检验工具UPPAAL进行自适应软件时间特性分析和验证。
1 相关工作
软件自适应已成为软件工程领域所关注的一个焦点问题,从IBM的自治计算(autonomic computing)[9]、美国军方的DASADA(Dynamic Assembly for System Adaptability, Dependability and Assurance)计划、每年国际软件工程大会ICSE(International Conference on Software Engineering)的SEAMS(symposia on Software Engineering for Adaptive and self-Managing Systems)研讨会、《软件学报》自适应软件专刊等中都可看出软件自适应问题研究的重要性,其中针对自适应软件的形式化建模方法的研究也吸引了众多研究学者。
课题组在前期工作中提出一种UML与时间自动机相结合的自适应软件建模方法[7],汲取了UML直观易理解和时间自动机严谨无二义性的优点,实现了自适应软件结构特征和行为特性的显式刻画和形式化验证。Ramirez等[10]提出了基于UML的设计模式,de la Iglesia等[5]总结并提炼出一套自适应软件形式化模板(formal templates),实现了自适应软件形式化模型的复用,降低了其形式化建模难度。此外,不少学者还探索使用进程代数CSP(Communicating Sequential Process)[11]、 Markov 模型[12]、 Petri网[13]等其他形式化工具进行软件自适应的形式化建模和分析,Weyns 等[14]作了较为详细的综述, 在此不再赘述。
上述这些研究的关注点集中在自适应逻辑的形式化描述与分析,其能够较好地刻画自适应过程的行为特性,并进行形式化分析和验证;然而,上述研究均未提供自适应软件动态过程时间特性的刻画与分析方法。实现自适应软件动态过程时间特性的显式定义和形式化描述是本文研究的动机。
Camilli等[15]提出一种基础时间Petri网(Time-Basic Petri nets)用于自适应软件各过程截止时间(deadline)和时间间隔(time interval)的刻画,实现了对时间攸关(time-critical)自适应系统的形式化建模与验证。Hachicha等[16]提出面向自适应软件的延迟时间(delay time)和逾期时间(expiry time)等时序性质,并提出通过扩展Event-B[17]模型形式刻画上述性质。上述研究开始关注自适应软件时间特性的刻画,对本文研究产生一定启发。同上述研究相比,本文更为系统地定义了自适应软件动态过程的时间特性,增加了自适应调节时间和自适应稳定时间等性能指标来定量评估自适应逻辑,本文还提供了一种基于时间自动机网络的自适应软件时间特性建模模板,实现建模方法的复用,降低自适应软件时间特性的刻画难度。
此外,Calinescu等[12]、Filieri等[18]和Ghezzi等[19]还考虑了自适应软件中时间特性的不确定性,提出将时间特性作为一种非功能需求(non-functional requirement)进行分析,利用概率模型检验(probabilistic model checking)的方法分析了响应时间(response time)等时间特性。同上述研究相比,本文侧重面向时间攸关领域(time-critical)的自适应软件时间特性的显式定义、形式化建模和分析验证。除响应时间(在本文为自适应调节时间)外,本文还较为系统地定义了延迟触发时间、截止时间等时间特性。
2 自适应软件时间特性定义
2.1 自适应软件MAPE-K模型
IBM 提出的MAPE-K[20]自治计算模型已广泛应用于自适应软件的设计中,它将自适应软件系统分为自适应逻辑和应用逻辑两部分。自适应逻辑由监控(Monitor)、分析(Analyze)、规划(Plan)和执行(Execute)四个模块外加一个知识库(Knowledge)模块构成,其中:监控模块用于从应用逻辑抽取属性或状态信息;分析模块用于判定系统中的错误和异常,如某一系统属性是否越限等;规划模块主要侧重于当发现系统出现问题时决定采用何种动作;执行模块关注于执行规划阶段所选择的自适应动作,对软件自身施加影响以应对变化;知识库模块存储系统自适应策略、历史数据等。如图1所示。
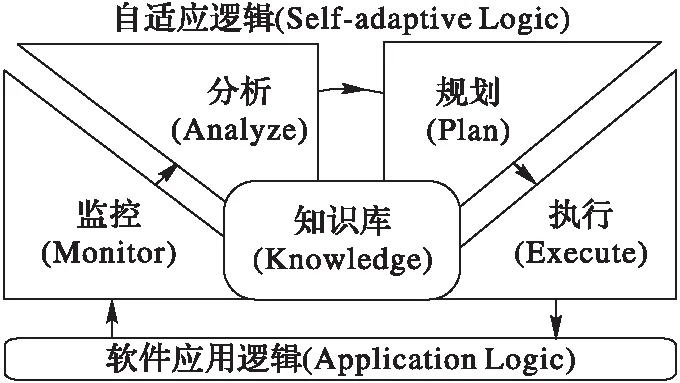
图1 MAPE-K自适应软件模型 Fig. 1 MAPE-K self-adaptive software model
MAPE-K模型定义了自适应软件的结构组成和自适应动态过程。然而,自适应软件能否正确运行,不仅要考虑自适应动态过程中各子过程行为的正确性,而且要考虑各子过程的时间特性,本文将以MAPE-K自适应模型为基础,定义和刻画自适应软件动态过程的时间特性。
2.2 典型自适应场景
SUIS(Ship sUpplying Information System)[21]是一个基于服务(Web-service)的舰船保障信息系统,其以服务的形式实时处理舰船提交的保障需求。在出航任务密集时期,SUIS要在短时间内处理大量的保障需求,为保证系统能够及时响应服务请求,SUIS以云架构(cloud-based architecture)的形式来实现,并构建自适应逻辑以动态监测和调整云端资源(计算节点和存储节点),满足动态变化的用户需求,系统整体架构如图2所示。
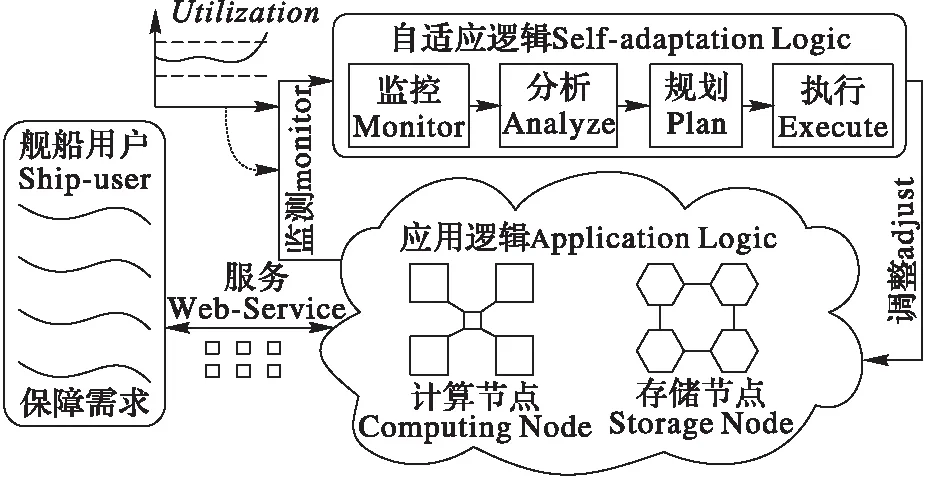
图2 基于云架构的舰船保障自适应信息系统 Fig. 2 Self-adaptive ship supplying information system based on cloud computing architecture
为提高服务保障的快速性和准确性,自适应逻辑需周期性监测云端服务器的CPU利用率(CPU Utilization),并根据CPU利用率的变化动态调整服务器池中服务器的数量(ServerNumber);此外,还需对自适应决策的每个子过程(MAPE的各个过程)进行时间约束,以提高云端响应的准确性。例如,自适应策略“ifUtilization>MforNseconds, then addPmore VMs”定义如果服务器CPU利用率在N秒内都超过上限值M,则添加P台虚拟机(Virtual Machine, VM),该策略在分析(Analyze)阶段添加延时触发时间约束N,能够提高监测的准确性。此外,该案例还需刻画监测周期、自适应动态过程的截止时间、自适应调节时间等时间约束,将在下文结合案例详细阐述。
2.3 自适应软件时间特性分析与定义
自适应软件时间特性用以约束自适应软件动态过程(如监控、分析、规划和动作等)的时间特性。如图3所示,自适应逻辑需定期监测软件上下文状态并依此决定是否启动自适应过程,为此,在软件自适应的监控阶段定义监控周期MPeriod,使其周期性抽取软件上下文状态信息(如2.2节自适应场景中CPU利用率Utilization),并触发后续自适应过程;在分析阶段定义延迟触发时间ADelay,在监控变量发生越限行为(如案例中Utilization>M)时,再持续监测ADelay时间(如案例中Nseconds),若监测变量仍然越限则触发后续自适应过程,定义延迟触发时间可以提高监测准确性;由于自适应规划和执行阶段需进行较为复杂的计算,在此定义截止时间PDeadline和EDeadline来限制自适应逻辑的时间开销,各时间特性定义如表1所示。

图3 自适应软件动态过程时间特性示意 Fig. 3 Temporal properties of self-adaptive software dynamic processes
如图4所示,自适应软件在面临变化时会作出响应以及时消除或减轻变化带来的不利影响,最终使系统恢复稳定状态。然而,如何评价自适应响应的及时性以及自适应响应带来的效果,现有研究尚缺乏相应的衡量指标。为此,本文定义了自适应调节时间TAdjust和自适应稳定时间TSteady,如表1所示,TAdjust表征系统在遭遇变化后恢复正常状态的快速性,TSteady表征系统遭遇变化后恢复稳定状态的快速性。自适应软件开发人员可根据实际需求不断优化软件自适应策略,使系统的自适应调节时间和自适应稳定时间降到最低。
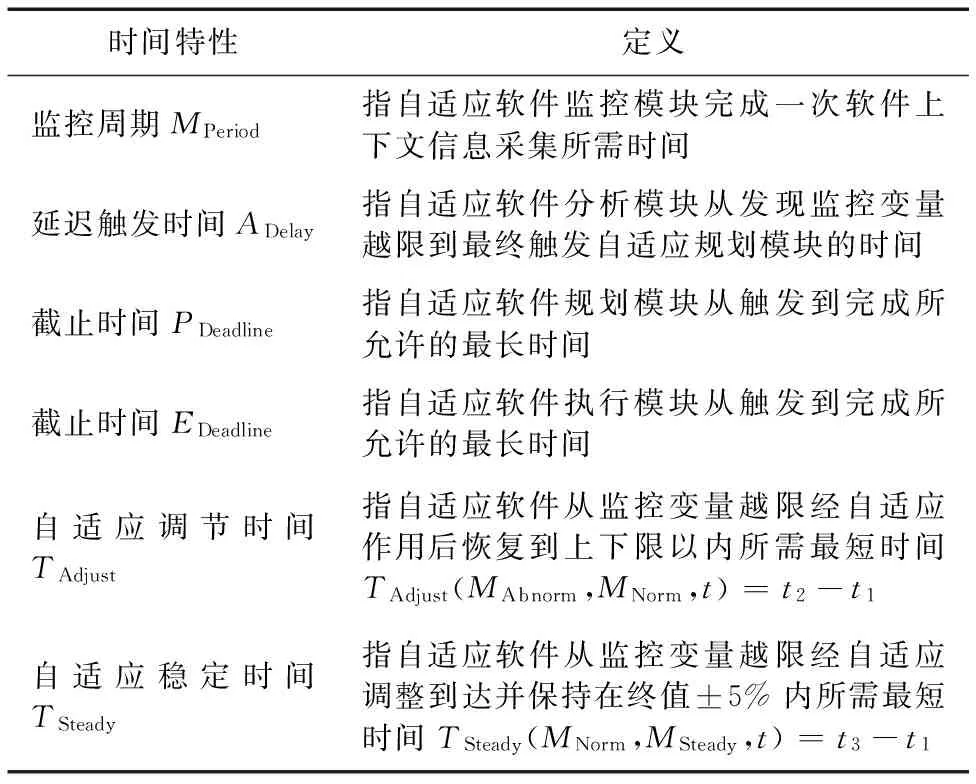
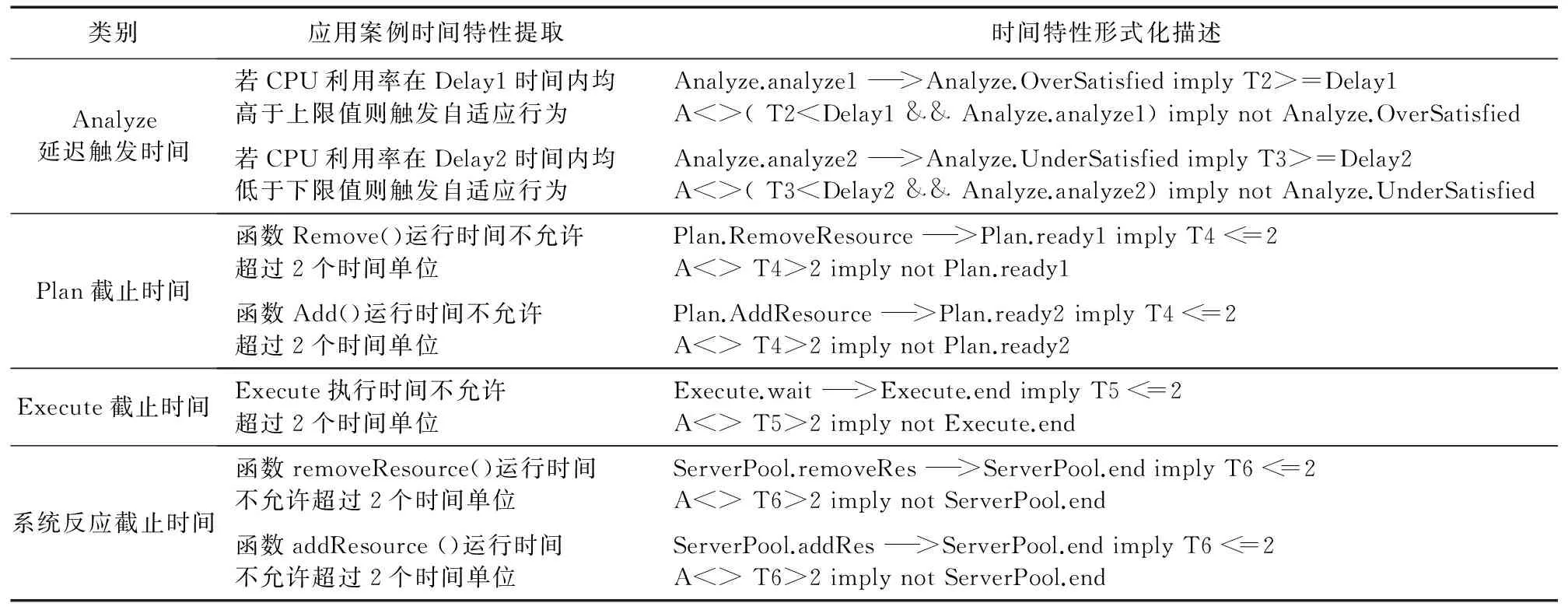
表1 自适应软件动态过程时间特性定义Tab. 1 Definitions of temporal properties of self-adaptive software dynamic processes
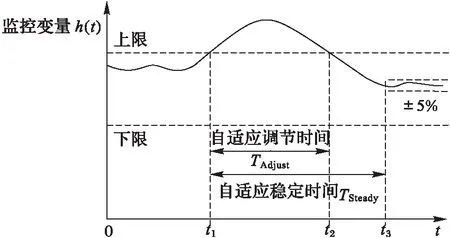
图4 自适应调节时间和稳定时间示意 Fig. 4 Self-adaptive adjusting time and steady time
3 自适应软件动态过程时间特性建模
时间自动机模型在自适应系统形式化建模领域取得了良好的应用效果,然而,现有研究鲜有考虑自适应软件的时间特性。为此,本文在现有研究基础上构建了基于时间自动机的自适应软件动态过程时间特性建模模板,实现自适应软件时间特性的显式刻画和形式化模型的复用。
3.1 时间自动机模型
时间自动机模型(timed automata)[22]对传统有限自动机模型进行了扩展,加入了时间约束,以支持对系统实时特性的描述和形式化分析,其可定义为一个六元组:TA〈L,l0,S,A,E,I〉。其中:L是有限位置的集合,L⊆Location;l0∈L表示初始位置initiallocation;S是边E上约束的集合,S⊆Guard;A是所有动作的集合,包括输入、输出和内部三类动作,A={a!|a∈Chan}∪{a?|a∈Chan}∪{τ};E是有向边的集合,E⊆L×A×G(c,v)×U(c,v)×L, (l,a,g,u,l′)表示从位置l到位置l′ 的迁移,迁移过程伴有卫式约束g、赋值操作u和动作a;I是不变式invariant的集合;I⊆Guard用以约束位置的状态。
由多个并发时间自动机模型可组成一个时间自动机网络模型(Timed Automata Network, TAN),记为:TAN≡TA1‖TA2‖…‖TAn。
模型检验工具UPPAAL[23]采用时间自动机网络模拟实时系统的行为,采用时序逻辑(Timed Computation Tree Logic, TCTL)刻画系统的性质,并对系统进行自动化分析和验证。
3.2 自适应软件动态过程时间特性建模模板
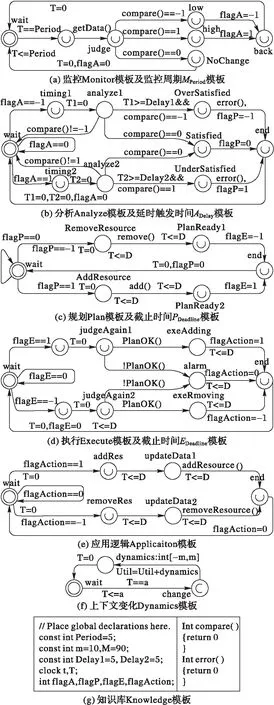
自适应软件的形式化建模难度大、耗时长,其行为特性较难刻画。为此,本节基于时间自动机网络构建了自适应软件动态过程时间特性建模模板,以显式刻画自适应软件的动态行为及时间特性,实现自适应软件形式化模型的复用,如图5所示。本文用时间自动机模型刻画“Monitor-Analyze-Plan-Execute”自适应软件动态过程,用“声明(declaration)”刻画“知识库(Knowledge)”,用时钟clock、卫式guard和不变式invariant刻画自适应软件的时间特性。
具体而言,监控Monitor模板如图5(a)所示,其将Monitor分为“定时-数据获取-比较-触发”四个阶段,在定时阶段通过guard和invariant组合定义监控周期T=Period;在数据获取阶段,通过getData()函数获取监控数据;在“比较”阶段通过将监控数据和设定的上下限比较,确定监控数据低于下限状态“low”或高于上限状态“high”或处于上下限之间“NoChange”,并根据不同状态触发不同分析标志flagA=-1,flagA=1或flagA=0。
分析Analyze模板如图5(b)所示,其由flagA触发,分为“延时-比较-触发”三个阶段,在延时阶段定义延迟触发时间T1=Delay1和T2=Delay2,若在延迟时间内监控数据保持越限状态,则判定系统处于资源“过满足OverSatisfied”或“不满足UnderSatisfied”状态,并触发相应的规划标志flagP。
规划Plan模板如图5(c)所示,其由flagP触发,在该模板中定义了截止时间T<=D,用来限制规划函数add()和remove()的时间开销。类似地,本文定义了执行Execute模板和应用逻辑Application模板,及相应的截止时间模板,如图5(d)和5(e)所示。
此外,为模拟软件上下文变化带来的影响,本文定义了上下文变化Dynamics模板,其能够周期性地产生一个位于[-m,m]的随机量,用以模拟环境干扰,如图5(f)所示。本文在自动机的声明declaration中构造了知识库Knowledge模板,用来定义自适应过程的相关变量和函数,如图5(g)所示。在Knowledge中还定义了全局时钟变量t,它能够记录监控变量发生变化的各个时刻,为后续自适应调节时间TAdjust和自适应稳定时间TSteady的分析作准备。
4 自适应软件时间特性分析与验证
在前期研究[7]中,课题组针对自适应软件有无死锁、自适应动作有效性等性质进行了形式化描述和验证,下文将在3.2节建立的形式化模板基础上,用定时计算树逻辑(TCTL)刻画自适应软件的延迟触发时间和截止时间等时间特性,并借助时间自动机UPPAAL进行验证。
4.1 自适应软件延迟触发时间验证
以图5(b)为例,该延迟触发时间特性可描述为“如果函数compare()在延迟时间Delay1结束后仍然等于-1,则变迁analyze1到OverSatisfied发生”。上述性质成立需同时满足两个条件:1) 若变迁从analyze1到OverSatisfied发生,则T1>=Delay1;2) 当T1 Analyze.analyze1-->Analyze.OverSatisfied imply T1>=Delay1 与 A<>( T1 类似地,可验证延迟触发时间特性“如果函数compare()在延迟时间Delay2结束后仍然等于1,则变迁analyze2到UnderSatisfied发生”。延迟触发时间特性描述与验证结果如图6所示。 以图5(c)为例,该截止时间特性可描述为“变迁从RemoveResource到PlanReady1的时间不能超过D”。上述性质成立需同时满足两个条件:1) 若变迁从RemoveResource到PlanReady1发生,则T<=D;2) 当T>D时,变迁从RemoveResource到PlanReady1不允许发生。该截止时间用以限制函数remove()在D时间内必须执行完毕。上述条件可形式化描述为: Plan.RemoveResource-->Plan.PlanReady1 imply T<=D 与 A<> T>D imply not Plan.PlanReady1 类似地,可验证截止时间特性“变迁从AddResource到PlanReady2的时间不能超过D”,截止时间形式化描述与验证结果如图7所示。 图5 自适应软件动态过程时间特性建模模板 Fig. 5 Modeling templates of temporal properties of self-adaptive software dynamic processes 本节以3.2节建立的自适应软件形式化模板为基础,给出了自适应软件延迟触发时间和截止时间的验证方法,具有一般应用意义。针对自适应调节时间和稳定时间的分析将在第5章结合具体案例详细说明。 图6 自适应软件延迟触发时间形式化描述与验证 Fig. 6 Formal description and verification of self-adaptive software delay trigger temporal properties 图7 自适应软件截止时间形式化描述与验证 Fig. 7 Formal description and verification of self-adaptive software deadline temporal properties 本章将以2.2节自适应场景为例,应用第3章提出的自适应软件动态过程形式化建模模板和第4章提出的自适应性质描述方法进行系统建模和性质验证。 图8展示了该自适应系统的形式化模型,本文定义了两个Dynamics模型分别模拟CPU利用率突然上升和突然下降的场景,自适应逻辑Monitor-Analyze-Plan-Execute和应用逻辑ServerPool构成了自适应闭环反馈系统。其中Monitor定期监控(周期为T1)服务器池ServerPool中服务器的CPU利用率(变量Utili)并将其传给变量Data,若Data越限,将通过触发标志flagA触发Analyze;在Analyze中将持续监控Delay1或Delay2时间段,若变量Data在该延迟时间段内仍然越限,则判定系统为“过满足(OverSatisfied)”或“不满足(UnderSatisfied)”状态,并通过flagP触发Plan;在Plan阶段根据系统偏离正常值的程度(以变量DUm和DUM表示)规划自适应策略,在此定义了时间约束T4限制remove()和add()函数的执行时间小于2个时间单位,Plan通过flagE触发Execute;在Execute阶段执行自适应策略,类似地,定义时间约束T5限制其执行时间,Execute通过触发标志flagAction将自适应动作施加到ServerPool上;应用逻辑ServerPool通过增/减投运服务器的数量SerNum使CPU利用率恢复正常状态。 5.1节的形式化模型构成了时间自动机网络模型:TAN={Monitor,Analyze,Plan,Execute,ServerPool,Dynamics},通过将其载入UPPAAL模拟器和验证器可进行自动化模拟分析和形式化验证。 1)系统有无死锁。输入命令A[ ]not deadlock检测系统是否有死锁现象,若存在死锁,通过模拟器 simulator模拟自适应行为,找到发生死锁时各自动机所处状态,及时调整模型,其验证结果如图9所示。 2)自适应动作有效性。该性质用于验证自适应软件的自适应动作能否得到有效执行,在上述案例中提炼以下四条性质进行验证: E<>ServerPool.removeRes E<>Execute.exeRemoving E<>ServerPool.addRes E<>Execute.exeAdding 其验证结果如图9所示。 3)时间特性。为验证舰船保障自适应信息系统的时间特性,本文将其分为延迟触发时间、截止时间、自适应调节时间和稳定时间等性质进行验证。根据第4章时间特性形式化描述模板,应用案例的延迟触发时间和截止时间的形式化描述如表2所示,其验证结果如图9所示。其中,图9(a)验证了在应用案例CPU利用率突然上升时,自适应软件动态过程的时间特性是否满足;图9(b)验证了在应用案例CPU利用率突然下降时,自适应软件动态过程的时间特性是否满足。 图8 舰船保障自适应信息系统形式化模型 Fig. 8 Formal model of self-adaptive ship supplying information system 表2 应用案例时间特性形式化描述 Tab. 2 Formal descriptions of temporal properties for the application example 类别应用案例时间特性提取时间特性形式化描述Analyze延迟触发时间若CPU利用率在Delay1时间内均高于上限值则触发自适应行为Analyze.analyze1-->Analyze.OverSatisfiedimplyT2>=Delay1A<>(T2 通过在UPPAAL中模拟仿真所建立的形式化模型,记录了案例模型在不同自适应场景下CPU利用率Utilization随时间t的变化过程,得到应用案例的自适应调节时间特性和自适应稳定时间特性,如图10所示。在CPU利用率突然下降时,系统通过自适应调节,经过17个单位时间后CPU利用率恢复到上下限以内(30%),由于监控的延时性,自适应过程继续作用,系统经30个单位时间恢复稳定状态(55%),如图10(a)所示。类似地,在CPU利用率突然上升时,系统经过16个单位时间恢复到上下限范围,并保持在稳定状态(74%)。 图9 应用案例形式化验证结果 Fig. 9 Formal verification results of the application example 从5.2节实验结果可以看出,本文方法除了支持系统死锁和自适应动作有效性等自适应动态过程行为的分析和验证外,还能有效支持自适应软件时间特性的分析。在表2中描述了案例系统对延迟触发时间和截止时间等特性的设计要求,并给出了相应要求的形式化描述,在图9中通过将上述性质载入UPPAAL可以直观地验证延迟触发时间和截止时间是否得到满足。针对自适应调节时间和自适应稳定时间不能够直接进行验证,需通过分析系统模拟仿真轨迹(trace)建立监控变量和时间的关系进行分析,如图10所示,可以直观分析CPU利用率随时间的变化,并根据图4中的定义确定自适应调节时间和自适应稳定时间,判断其是否满足用户需求。综上所示,本文方法能够直观和有效地进行自适应软件时间特性的分析和验证。 图10 应用案例的自适应调节时间和自适应稳定时间特性 Fig. 10 Self-adaptative adjusting time property and self-adaptative steady time property of the application example 自适应软件的建模与验证方法研究已成为软件工程领域的前沿热点研究问题。在现有自适应建模与验证方法中较少考虑系统的时间约束,然而,在时间攸关应用领域,自适应软件的正确运行不仅依赖于自适应逻辑的正确性,而且依赖于自适应软件动态过程的时间特性。为此,本文定义了监控周期以显式刻画监控Monitor的时间特性;定义了延迟触发时间,来刻画类似“ifUtilization>MforNseconds”这种分析Analyze阶段的延迟性;定义了自适应过程截止时间,用以约束Plan、Execute等的执行时间,以降低自适应逻辑的时间开销;定义了自适应调节时间和稳定时间以定量评估自适应逻辑的响应速度和响应效果。此外,本文还定义了一种基于时间自动机网络的自适应软件动态过程时间特性建模模板,实现建模方法的复用,降低自适应软件形式化建模难度。最后,本文将自适应软件时间特性形式化描述为TCTL形式,并载入到时间自动机工具UPPAAL中,进行自适应软件动态过程时间特性的形式化分析和验证。本文以舰船保障自适应信息系统为例,分析和验证了在遭受不同环境变化时系统的自适应行为和自适应动态过程的时间特性,从而验证了本文方法的有效性。 本文用时间自动机模型刻画自适应软件的动态过程,当系统规模和复杂度较大时,建模难度增大,系统模型检验时会出现状态空间爆炸(state-space explosion)的问题,下一步考虑将自动机模型与Event-B[18]模型相结合,构建一种逐步精化(stepwise refinement)的自适应软件形式化方法,降低其建模难度。 参考文献(References) [1] SALEHIE M, TAHVILDARI L. Self-adaptive software: landscape and research challenges [J]. ACM Transactions on Autonomous and Adaptive Systems (TAAS), 2009, 4(2): Article No. 14. [2] CHENG B H C, de LEMOS R, GIESE H, et al. Software engineering for self-adaptive systems: a second research roadmap [M]// Software Engineering for Self-Adaptive Systems, LNCS 5525. Berlin: Springer, 2013: 1-26. [3] KRUPITZER C, ROTH F M, VANSYCKEL S, et al. A survey on engineering approaches for self-adaptive systems [J]. Pervasive and Mobile Computing, 2015, 17(Part B): 184-206. [4] 杨启亮,马晓星,邢建春,等.软件自适应:基于控制理论的方法[J].计算机学报,2016,39(11):2189-2215.(YANG Q L, MA X X, XING J C, et al. Software self-adaptation: control theory based approach [J]. Chinese Journal of Computers, 2016, 39(11): 2189-2215.) [5] de la IGLESIA D G, WEYNS D. MAPE-K formal templates to rigorously design behaviors for self-adaptive systems [J]. ACM Transactions on Autonomous & Adaptive Systems, 2015, 10(3): Article No. 15. [6] VOGEL T, GIESE H. Model-driven engineering of self-adaptive software with EUREMA [J]. ACM Transactions on Autonomous & Adaptive Systems , 2014, 8(4): Article No. 18. [7] 韩德帅,杨启亮,邢建春.一种软件自适应UML建模及其形式化验证方法[J].软件学报,2015,26(4):730-746.(HAN D S, YANG Q L, XING J C. UML-based modeling and formal verification for software self-adaptation [J]. Journal of Software, 2015, 26(4): 730-746.) [8] HAN D, YANG Q, XING J, et al. FAME: a UML-based framework for modeling fuzzy self-adaptive software [J]. Information & Software Technology, 2016, 76: 118-134. [9] MURCH R. Autonomic Computing [M]. [S.l.]: IBM Press, 2004: 535-539. [10] RAMIREZ A J, CHENG B H C. Design patterns for developing dynamically adaptive systems [C]// SEAMS ’10: Proceedings of the 2010 ICSE Workshop on Software Engineering for Adaptive and Self-Managing Systems. New York: ACM, 2010: 49-58. [11] BARTELS B, KLEINE M. A CSP-based framework for the specification, verification, and implementation of adaptive systems [C]// SEAMS ’11: Proceedings of the 6th International Symposium on Software Engineering for Adaptive and Self-Managing Systems. New York: ACM, 2011: 158-167. [12] CALINESCU R, GHEZZI C, KWIATKOWSKA M, et al. Self-adaptive software needs quantitative verification at runtime [J]. Communications of the ACM, 2012, 55(9): 69-77. [13] DING Z, ZHOU Y, ZHOU M. Modeling self-adaptive software systems with learning Petri nets [J]. IEEE Transactions on Systems, Man, and Cybernetics Systems, 2016, 46(4): 483-498. [14] WEYNS D, IFTIKHAR M U, de la IGLESIA D G, et al. A survey of formal methods in self-adaptive systems [C]// C3S2E ’12: Proceedings of the 5th International C*Conference on Computer Science and Software Engineering. New York: ACM, 2012: 67-79. [15] CAMILLI M, GARGANTINI A, SCANDURRA P. Specifying and verifying real-time self-adaptive systems [C]// ISSRE 2015: Proceedings of the 26th IEEE International Symposium on Software Reliability Engineering. Piscataway, NJ: IEEE, 2015: 303-313. [16] HACHICHA M, HALIMA R B, KACEM A H. Modeling and verifying self-adaptive systems: a refinement approach [C]// SMC 2016: Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, NJ: IEEE, 2016: 3967-3972. [17] ABRIAL J R. Modeling in Event-B: System and Software Engineering [M]. Cambridge, UK: Cambridge University Press, 2010: 176. [18] FILIERI A, GHEZZI C, TAMBURRELLI G. A formal approach to adaptive software: continuous assurance of non-functional requirements [J]. Formal Aspects of Computing, 2012, 24(2): 163-186. [19] GHEZZI C, PINTO L S, SPOLETINI P, et al. Managing non-functional uncertainty via model-driven adaptivity [C]// ICSE ’13: Proceedings of the 2013 International Conference on Software Engineering. Piscataway, NJ: IEEE, 2013: 33-42. [20] KEPHART J O, CHESS D M. The vision of autonomic computing [J]. IEEE Computer, 2003, 36(1): 41-50. [21] HAN D, XING J, YANG Q, et al. Handling uncertainty in self-adaptive software using self-learning fuzzy neural network [C]// COMPSAC 2016: Proceedings of the 40th IEEE Annual Computer Software and Applications Conference. Washington, DC: IEEE Computer Society, 2016: 540-545. [22] ALUR R, DILL D L. A theory of timed automata [J]. Theoretical Computer Science, 1994, 126(2): 183-235. [23] LARSEN K G, PETTERSSON P, YI W. UPPAAL in a Nutshell [J]. International Journal on Software Tools for Technology Transfer, 1997, 1(1/2): 134-152. This work is supported by the Natural Science Foundation of Jiangsu Province (BK20151451). HANDeshuai, born in 1990, Ph. D. candidate. His research interests include software self-adaptation, Cyber-Physical System (CPS). XINGJianchun, born in 1964, Ph. D., professor. His research interests include Cyber-Physical System (CPS), Building Information Model (BIM). YANGQiliang, born in 1975, Ph. D., associate professor. His research interests include software self-adaptation, Building Information Model (BIM). LIJuelong, born in 1959, M. S., professor. His research interests include building environment and equipment engineering.4.2 自适应软件截止时间验证


5 案例研究
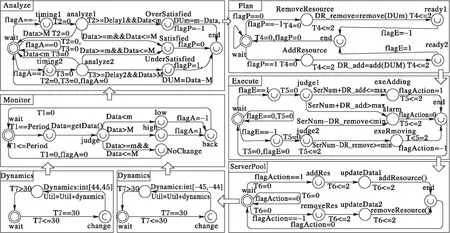
5.1 舰船保障自适应信息系统形式化建模
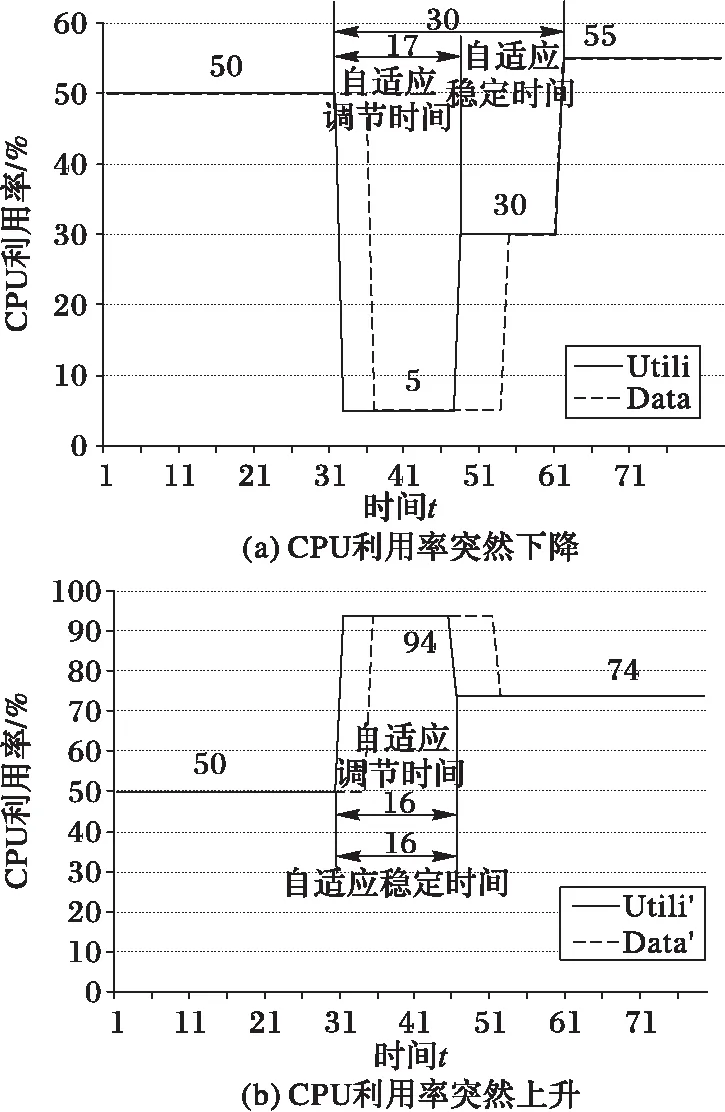
5.2 舰船保障自适应信息系统形式化验证
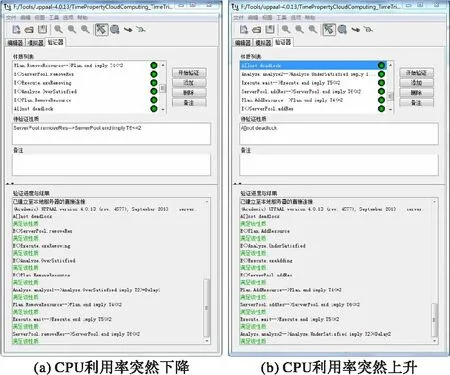
5.3 讨论
6 结语

