基于网络编码的确定性逐层构造算法
徐光宪,赵 越,赖俊宁
(辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛 125105)
0 引言
在传统网络通信中,节点只能对数据进行简单的存储和转发,不能对数据作任何处理。然而在2000年Ahlswede等[1]首次提出了网络编码的基本原理,其核心思想是允许中间节点对输入信息进行合理编码,然后将编码信息发送到下级节点,最后信宿通过解码矩阵对编码信息进行解码即可恢复出原始信息。Koetter等[2]提出了关于确定线性网络编码的代数构造方法,2005年Jaggi等[3]简化了文献[2]方法,把构造网络编码的复杂程度从指数级别降到了多项式级别,也使网络编码中使用的伽罗华域次数有所缩减[4-5]。随着研究的不断深入,线性网络编码构造算法被分成了随机线性网络编码构造算法[6]和确定线性网络编码构造算法[7]。随机线性网络编码是指在信息传输过程中从有限域中随机选取编码向量,并对接收到的信息进行编码,所以随机线性网络编码要求编码节点有较强的运算能力,并且当信宿点接收到了足够的数据后,就可以进行解码操作。与随机线性网络编码不同,确定线性网络编码是先确定编码向量,再进行数据传输。确定性网络通常指有线网络拓扑,其全局网络拓扑是固定的,编码节点的位置也是确定的,所以编码向量可根据全局网络拓扑知识来确定。由于确定性网络中间节点是通过固定链路连接的,链路拓扑动态变化表现在链路权值的波动,不存在节点移动和链路断路的情况,那么在不稳定网络拓扑中编码节点不断变化,随机线性网络编码构造算法更能发挥优势;而确定线性网络编码构造算法的编码节点位置是确定的,适用于网络状态较稳定的组播通信,其所需运算空间更小、运算量更少。
线性网络编码在国内外已经得到了广泛深入的研究,文献[5]基于线性编码找到了计算最大组播容量的分布式算法;王龙翔[8]在组播率小于组播容量的前提下,提出了有线网络编码路由算法;文献[9]涉及了静态多播连接时构造最小代价子图算法。然后研究者们又从网络拓扑入手,提出了多种网络编码算法:文献[10]提出了一种基于向量空间正交补的确定线性网络编码构造算法,该算法相对复杂需要消耗较长时间,适用在网络拓扑稳定的情况下;文献[11]在基于网络编码的多路径分簇路由算法的基础上,提出了一种分布式随机网络编码算法,该算法适用于拓扑变化频繁的分布式网络中;文献[12]针对网络拓扑未知的情况提出了一种基于信宿反馈的确定线性网络编码构造(Sink Nodes Feedback Deterministic Network Coding, SNFDNC)算法,该算法需要进行多次试播来确定编码方案,网络编码收敛时间较长;文献[13]提出了一种基于网络编码的分布式卫星路由算法和一种基于机会搜寻的随机网络编码构造算法,并将两种算法相结合实现了随机的网络编码组播通信;随后文献[14]在基于网络编码的多路径分簇路由算法的基础上,提出了一种分布式随机网络编码算法,该算法扩展性强,可成功移植到组播路由算法中,但由于该算法运用随机线性网络编码构造方案,所以不能充分利用带宽资源且运算量过大。
近年来,关于网络编码的研究已经从单源组播通信[2-4]过渡到了多源组播通信,文献[15-17]通过引入虚拟信源的方法对一般多源组播问题的网络容量进行研究,提高了链路吞吐量和组播系统的稳定性,但是算法复杂度普遍较高,使得收敛时间过长。其中:文献[15]提出了一种基于埃德蒙兹最大流的公平分层组播网络编码构造算法,通过运用多项式复杂度启发式方案来确保信宿接收信息的可解码性,但该算法需要反复寻找信源到信宿之间的增广路径,需要较长运算时间,只有在较大规模的网络拓扑中才能发挥其优势;文献[16]将网络编码分层组播应用于多媒体点对多点的资源分配中,通过多速率传输策略实现了网络拓扑中各层下行链路广播分组数的最小化,然而文中没有给出用于分配各层数据所需链路带宽的方案,导致网络带宽利用率较低;文献[17]为了降低网络延迟,提高网络传输效率,提出了一种最小化网络延迟的编码感知传输调度算法,其有效性在实验中得到了验证,并为路由和编码的联合设计提供了更多可能性;文献[18]提出一种基于多源组播的独立安全网络编码方案,保证了多播网络的安全性和可靠性,使大容量网络拓扑的形成成本有所降低,但该方案需要评估所有可能潜在的网络拓扑,因此需要很高的计算复杂度。
在基于网络编码的多源组播通信情形下,首先需要运用组播路由算法来确定路由方案;然后选取合适的网络编码构造算法来确定编码方案。文献[12]提出了一种基于信宿反馈的确性定网络编码构造(SNFDNC)算法,该算法在单源组播问题上,可以通过试播法确定组播容量和编码方案,试播过程中均采用随机线性网络编码方案。本文延续了文献[12]的基本思想,针对以上文献提到的网络编码算法的不足,以在链路状态可变的确定性网络中实现高效组播通信为目的,提出了一种可动态调整各编码节点局部编码向量的确定线性网络编码逐层构造算法(Deterministic Layered Structure algorithm based on Network Coding, DLSNC)。该算法只需通过一次虚拟试播即可由上到下逐层重构变换节点的局部编码向量,同时允许对输入数据冗余链路进行修剪枝,最终产生可行的局部编码向量方案,保证信宿成功解码。通过仿真测试证实:本文算法进一步提高了多源组播通信的平均传输速率,收敛时间更短,并提高了网络带宽利用率。
1 相关知识
1.1 网络编码多源组播原理
假设一个多源组播网络用有向无环二元组G(V,E)表示,V和E分别表示有限节点集和有限链路集,链路集为编码节点间的有向链路。设S={S1,S2,…,Sn}为各组播源点的集合,T={T1,T2,…,Td}为各信宿点的集合,在有向图中标记输入节点vi的链路集为ΓI(vi),输出节点vi的链路集为ΓO(vi),用|ΓI(vi)|和|ΓO(vi)|分别表示节点vi的入度和出度。在多源组播通信中,应该使组播率在不大于组播容量的前提下无限接近组播容量,编码节点可通过对输入信息进行编码来使组播容量等于理论上的最大流[19]。通常选取|ΓI(vi)|大于|ΓO(vi)|的节点为编码节点,其输出信道都有各自对应的编码器来存储编码向量,并对输入信息进行编码[20],编码器个数为|ΓO(vi)|。设d为编码节点v的输入链路,e为其输出链路,输入信息向量为y(d),输出编码信息向量y(e),y(d)与y(e)的关系如式(1)所示;输入全局编码向量为g(d)与输出的全局编码向g(e)的关系如式(2)所示:
(1)
(2)
其中:mde构成了输出链路e的局部编码向量,用m(e)表示,即:m(e)={mde∈GF(2m):d∈In[tail(e)]},其中m(e)的维数等于节点vi的输入链路数。
经过任一编码节点的输出信息向量均可看作是信源所发送信息的线性组合,该线性组合的系数就是编码节点输出链路e的全局编码向量。
1.2 伽罗华域
在伽罗华域GF(2m)中,m代表伽罗华域的次数,由既约多项式确定[5],q=2m代表伽罗华域的阶数,由于在固定伽罗华域中字符都是有限个相同数目的二进制字符串,这样计算较为方便,所以本文中确定线性网络编码运算都是在伽罗华域环境下进行的。令多源组播网络中的组播率为h,每个信道上传输的数据块长度为L个字符,因为采用的伽罗华域为GF(2m),则每个字符均为m比特的二进制数,那么组播通信一次数据传输的信息量为mLh比特。
在基于网络编码的组播通信中,无论是随机线性网络编码还是确定线性网络编码,数据包的数据字段都需要在编码节点进行字符间的编码运算[21],在伽罗华域中加法运算与减法运算相当于异或运算;乘法运算首先是将二进制多项式相乘,然后在合并同类项系数时同样采用异或运算;除法运算则是乘法的逆运算。网络编码时就是在执行乘法运算过程中将系数进行模2加后,对形成的多项式进行多次降次,直到其最高次数小于m,那么该多项式的系数就是对应字符的相应位。文献[5]证明了在伽罗华域上加减、乘法、除法的运算量分别为m、3m2和3m2+m3/3,依次用α(m),β(m)和χ(m)表示。在整个编码过程中,编码节点v的输入链路个数为|ΓI(v)|,输出链路个数为|ΓO(v)|,则每个输出信息向量分别需要进行|ΓI(v)|次乘法和|ΓO(v)|次加法,文献[5]也给出了编码节点v应用确定线性网络编码和随机线性网络编码的运算量,如式(3)和式(4)所示,确定线性网络编码和随机线性网络编码信宿节点T解码的运算量如式(5)和式(6)所示,可见确定线性网络编码的运算量远小于随机线性网络编码。本文提出的SNFDNC算法,就是在已知路由方案的网络拓扑中用确定线性网络编码为编码节点选取适当的编码系数后,对多个输入数据流进行多项式乘法并执行异或运算的过程。
τ(v)=L[α(m)+β(m)]|ΓI(v)||ΓO(v)|
(3)
τ(v)=(L+h)[α(m)+β(m)]|In(v)||Out(v)|
(4)
τ(T)=Lh2[α(m)+β(m)]
(5)
τ(T)=(Lh2+4h3/3)[α(m)+β(m)]+hχ(m)
(6)
在多源组播中,一次完整的数据传输是指:数据包从一个组播源发出后,要经过多个中间节点进行网络编码,然后传入信宿节点进行解码,直到最后一个组播信宿成功解码的过程,所以多源组播的一次数据传输延迟等于所有组播源中一次数据传输延迟的最大值。确定线性网络编码和随机线性网络编码组播一次群的运算延迟如式(7)和式(8)所示,确定线性网络编码延迟更短。通过分析得出影响运算延迟的因素仅与数据信息字符长度L和伽罗华域的阶数m有关[5]。
τ=L(w+h2)(3m2+m)
(7)
(8)
2 逐层构造网络编码方案
2.1 方案的理论依据
源点单位时间传递信息的速率称为组播率,最大组播率即为组播容量,它等于信源到信宿容量函数的最小值,也就是信源到信宿的最小割值[22]。在已知网络拓扑的多源组播网络G(V,E)中,信源集合为S=(S1,S2,…,Sn),且各源点相互独立,信宿集合为T=(T1,T2,…,Td),其中n>1,d>1。令z∈T,且∀D⊆S,记min-c(D,z)为信源集合D与信宿点z的最小割值,那么m-f(D,T)为信源集合D与每个信宿点最小割值的最小值,也就是信源集D到信宿集T的最大流,如式(9)所示。在多源组播网络拓扑中加入一个虚拟信源S′后,m-f(D,T)用m-f(S′,T)表示。
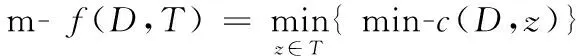
(9)
网络拓扑中每条链路的链路容量可用该链路的最大传输速率来表示,若链路容量为C,C大于1且C为正整数,则该链路可看作是由C条链路容量为1的信道构成。
定理1 在多源组播网络拓扑中,如果虚拟信源和各组播源点只采用路由方式传递信息并不进行编码,且每个源点需传输信息到全部信宿点,设各个源点的组播率分别为h1,h2,…,hn,那么当S′的组播容量与其输出信道数关系满足式(10),S′的组播率h与各个源点的组播率关系满足式(11)时,则一定可以找到一个可行的网络编码方案[20]。
m-f(S′,T) = |Out(S′)|
(10)
(11)
证明 由式(9)可证式(10)成立。又因为虚拟信源和实际信源只进行数据传输不进行编码,所以用虚拟信源代替实际信源时,只需令虚拟信源信道数等于各信源信道数之和即可。而且每个源点需要传输信息至全部宿点,那么通过调整各编码节点的局部编码向量使每个信宿点接收到满秩的全局编码矩阵则代表编码成功,证明原理如图1所示。
组播网络通过组播路由算法生成组播路由方案确定了编码节点的位置,但是在数据传输的整个过程中,网络拓扑的动态变化会引起路由方案的变动(主要体现在链路权值的变化),这就需要重构信道的局部编码向量来形成一个新的可行编码方案。
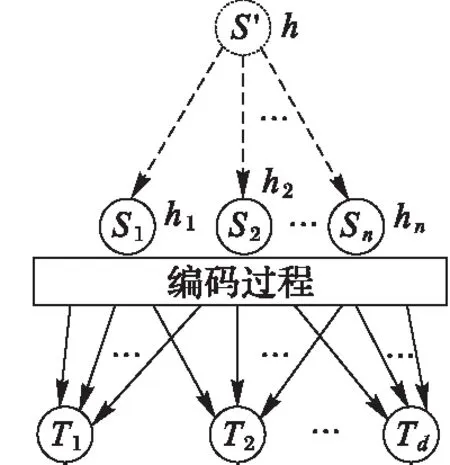
图1 虚拟信源示意图 Fig. 1 Schematic diagram of virtual source
确定线性网络编码可以在网络拓扑已知的前提下,采用集中方法构造网络编码方案[23],通过调整部分编码节点的局部编码向量使每个节点收到的全局编码矩阵满秩,保证每个信宿获得的解码矩阵可以成功解码。
定义1 在已知全局网络拓扑的前提下,采用确定性网络编码,以给定组播率由上而下逐层进行局部编码向量的构造,数据传输过程中采用这些编码向量进行编码运算,则称为确定线性网络编码逐层构造策略。
定义2 虚拟源点发送的数据包逐层经过编码节点,同时每层节点将其收到的全局编码矩阵反馈给上层与之相关的编码节点,直到信宿完成反馈,该过程称为一次虚拟试播[12]。
由于在虚拟试播阶段只需要考察各节点接收到的全局编码矩阵,而并不需要考察其接收到的数据信息,所以试播虚拟矩阵即可。因为虚拟信源组播率为h,所以要发送h×h阶试播矩阵,实验包结构中的数据段可以忽略不进行传递,其格式如图2所示。

图2 实验包结构 Fig. 2 Structure of test package
定理2 虚拟试播过程中,如果虚拟信源的试播矩阵以及中间节点的全局编码矩阵是满秩的,那么一定存在可行的线性网络编码方案。
证明 令虚拟信源在一个时隙T内发出h个数据包,它们包含h个原始信息向量和h个全局编码向量,设每个信息向量长度为L字符,便构成了L×h阶原始信息矩阵Aorig。在传递过程中,信息需要经过中间节点进行编码,即对h个虚拟信源的全局编码向量进行线性组合生成新的全局编码向量,最终每个信宿Ti都会接收到一个h×h阶全局编码矩阵B以及L行h列的编码信息矩阵Y。而通常为了保障网络编码的安全性,需要用h×h阶的信源加密矩阵G对原始信息进行加密处理,最终得到网络编码矩阵变换公式如(12)所示,解码公式如(13)所示:
AorigGB=Y
(12)
Aorig=[(AorigG)B](GB)-1
(13)
本文进行试播时无需对信息进行传递,所以可将试播矩阵近似看成加密矩阵G,由矩阵论知识得出:只有保证试播矩阵G和全局编码矩阵B满秩,才能形成可行的线性网络编码方案,成功恢复出原始信息矩阵Aorig。
定理3 试播矩阵的选取是随机的,令M1是n×n阶对角线以下元素都是0的上三角矩阵,M2是n×n阶对角线以上元素都是0的下三角矩阵,M1和M2的对角线都是非零元素,那么M1×M2便可得到满秩的试播矩阵G。
证明 因为M1是上三角矩阵,M2是下三角矩阵,同时二者的对角线都是非零元素,所以矩阵M1和M2是满秩矩阵,那么两个满秩矩阵相乘得到的矩阵也是满秩的,即试播矩阵满秩。试播矩阵的确定就是按照定理3的方法,在伽罗华域中随机选取的。
2.2 逐层构造网络编码算法
本文通过虚拟试播运用确定线性网络编码逐层构造策略进行局部编码向量可行方案的确定。由定理3可知:只要在伽罗华域GF(2m)上随机选取元素构成矩阵M1和M2即可确定试播矩阵,由于网络编码对编码节点的运算能力和存储空间有较高要求[22],所以本文为了计算方便,试播矩阵选用h×h阶的单位矩阵E,这样输入节点vi的编码信息就等于一个由旧全局编码向量组成的L×|ΓI(vi)|阶矩阵,如式(14)所示,那么输出到链路e的信息向量等于输入信息向量与编码节点vi的局部编码向量之积,也就是编码节点vi新生成的全局编码向量,如式(15)所示,最后信宿节点收到的编码信息矩阵C就是其全局编码矩阵B。
[L×|ΓI(vi)|]=E×[h×|ΓI(vi)|]=
[h×|ΓI(vi)|]
(14)
y(e)=[h×|ΓI(vi)|]×(c1,c2,…,c|ΓI(vi)|)T=g(e)
(15)
定义3 在确定局部编码向量可行方案时,用Mij表示输入节点vij的全局编码矩阵,用RM表示Mij的秩,用p代表每层获得非满秩全局编码矩阵的节点个数。若Mij非满秩,则需改变vij的上层编码节点的局部编码向量,以确保矩阵Mij满秩,称符合变换要求的第i-1层的编码节点为潜在变换节点,其数目记为q;称潜在变换节点中改变了局部编码向量的编码节点为变换节点。
在已知路由方案的情况下,多源组播网络采用线性网络编码方法传递数据,设共有f层网络节点,f=1代表组播源点集,源点不进行编码,k为同层编码节点总数,vij表示第i层第j个编码节点,其中i和j的取值都为正整数且2≤i≤f,0≤j≤k,信宿为第f层编码节点。在试播过程中,vij的输入链路数与输出链路数分别为|ΓI(vij)|、|ΓO(vij)|,当p>0时,需要改变与vij对应的变换节点的局部编码向量以确保vij得到的全局编码矩阵满秩。
定义4 在数据传输过程中,当编码节点的部分输入链路无法为网络编码提供有用数据时,则对其进行修剪,该过程称为修剪枝。
例如多条链路传送相同或线性相关信息到同一编码节点时,便可对其中部分链路进行修剪。在网络编码时进行修剪枝,可以减少数据冗余,避免链路复用,从而提高网络带宽利用率。
在进行统计各层获得非满秩全局编码矩阵节点个数时,采用了决策树算法[24]。决策树是一类常见的机器学习方法,它以一种树形结构对样本进行分类,其中每个节点代表一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。其中C5.0决策树算法[24]有着非常好的泛化能力和鲁棒性,可以对训练样本中“变化”和“未变化”的样本进行高度识别与区分,最终得到正确分类。
本文在网络拓扑发生动态变化后,就是利用C5.0决策树算法自动提取检测网络拓扑中各层节点的编码矩阵,然后对编码节点进行重新分类的,其中一类是获得满秩全局编码矩阵的节点;另一类是获得非满秩全局编码矩阵的节点。同时,C5.0决策树算法还可以对各类样本的数目进行统计。该算法将网络拓扑中所有节点作为训练样本集,通过训练会具有很好的泛化能力,所以可快速准确地找到变换和未变换的样本。本文需要统计的是各层未获得满秩全局编码矩阵的节点,其数目用p表示。
1)当p=0时,证明第i层编码节点全部得到了满秩的全局编码矩阵,则跳到第i+1层继续判断。
2)当p>0时,证明第i层存在p个编码节点得到了非满秩全局编码矩阵,接下来查找这些编码节点的上层潜在变换节点数q:
① 当q=|ΓI(Vij)|-RMij时,令q个潜在变换节点全部成为变换节点。
② 当q>|ΓI(Vij)|-RMij时,首先进行潜在变换节点优先级的判定,即编码节点的输入链路数目越少,其重构局部编码向量的运算量越低,优先级越高。通过优先级判定从q个潜在变换节点中选出|ΓI(Vij)|-RMij个变换节点,若优先级相同,则任选其一即可。
③ 当q<|ΓI(Vij)|-RMij时,令q个潜在变换节点都为变换节点的同时要对组播路由方案进行修剪枝,去掉与该编码节点相连的|ΓI(Vij)|-RMij-q条相关上游链路,也就是修剪掉数据冗余链路,减少网络开销,提高带宽利用率。
本文以一个已经确定了组播路由方案的18节点无向图来展示确定线性网络编码逐层构造算法的原理,如图3所示,设入度大于1的网络节点可以作为编码节点,初始局部编码向量组成全部默认为1,组播信宿数|T|=4,有4层网络节点(虚拟信源不参与计数),用f=4表示。
图3中引入了虚拟信源S′,试播矩阵为4×4阶的单位矩阵,S1=(1 0 0 0)T,S2=( 0 1 0 0)T,S3=( 0 0 1 0)T,S4=( 0 0 0 1)T。下面对确定线性网络编码逐层构造算法进行举例说明,在信宿层节点通过决策树算法得知信宿点T2全局编码矩阵的秩为3,未获得满秩全局编码矩阵,所以要重构其上层变换节点V2.1的局部编码向量,最终使信宿点T2获得满秩的全局编码矩阵,如式(16)所示:
(16)
在图3中还可以看到算法对编码节点V2.5的输入链路进行了修剪枝,因为它的输入全局编码矩阵的秩小于输入链路数目,是非满秩矩阵,它的上层潜在变换节点数为0,所以要对其进行修剪枝,减少链路冗余,提高网络带宽。编码节点的输出链路对应着各自的编码器,在确定变换节点后,需要重构其相应输出链路编码器的编码系数,从而生成新的编码向量,直至同层所有变换节点完成了局部编码向量的重构,再将新生成的编码向量重新输入到各自对应的第i层的p个编码节点。然后,这些编码节点再次计算各自的输入全局编码矩阵是否满秩,循环至p=0便进入到下一层编码节点的局部编码向量构造。重复以上操作,直到信宿层的全局编码矩阵Bi满秩,即编码成功。
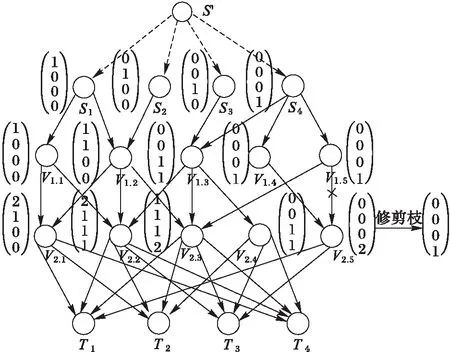
图3 DLSNC原理示意图 Fig. 3 Schematic diagram of DLSNC
2.3 逐层构造网络编码算法流程
算法描述:
步骤1 算法初始化。
步骤2 虚拟信源发送试播矩阵,同层编码节点开始编码,各编码节点为其输出信道产生全局编码向量,按式(15)计算出输出信道全局编码向量并转发实验包。
步骤3 运用决策树算法标记出p个第i层获得非满秩全局编码矩阵的编码节点vij,若p=0,层数i自加并跳转到下一层编码节点,若p>0,需要调整vij的上层变换节点编码向量。
步骤4 当p>0时,标记与编码节点vij对应的第i-1层潜在变换节点位置,并计数为q。
1)当q=|ΓI(Vij)|-RMij时,令q个潜在变换节点全部成为变换节点;
2)当q>|ΓI(Vij)|-RMij时,进行潜在变换节点优先级的判定,确定变换节点;
3)当q<|ΓI(Vij)|-RMij时,令q个潜在变换节点都为变换节点并进行修剪枝。
步骤5 确定变换节点后,调整其局部编码向量,将新生成的全局编码向量再次传入编码节点vij,不断循环,直到使vij输入链路的全局编码向量满秩。
步骤6 Untilp=0。
步骤7i+1→i。
步骤8 Untili=f。
步骤9 最终得到局部编码向量可行方案,算法结束。
2.4 算法复杂度分析
通过上述算法可以得到确定性网络编码方案,用邻接链表表示网络拓扑,用Steiner树可以实现总代价最小分布树的方法来保证网络链路开销最小。在随机线性网络编码构造算法中,编码节点的编码系数是随机选取的,而在确定性网络编码方案中需要通过计算得到编码节点的编码系数。本文算法只需进行一次虚拟试播,设虚拟信源的组播率为h,Vc为编码节点,D为Steiner节点,则算法的整个复杂度表示为O[|Vc||D|h(|D|+h)]。
3 仿真测试
本文仿真实验环境为Dell PC,处理器为Intel Core- M480 I5 CPU @2.67 GHz、4 GB内存,操作系统为32位Windows 7系统,安装并使用了VC++6.0、CygWin、Matlab R2011b和NS2-allinone2.26软件。
对已知组播路由方案的多源组播网络进行仿真测试,实验环境为NS2自带的拓扑生成工具GT-ITM生成的K均值聚类Waxman随机拓扑模型——KRTG(Random Topology Generate algorithm based onK-means)[25],通过在KRTG模型中设置节点数、节点范围、链路带宽、链路长边与短边等参数来形成不同规模的网络拓扑。其基本原理是将设制的n个节点均匀分布在拥有最大距离上限的平面上,节点间生成链路的概率如式(17)所示:
(17)
其中:|V|表示节点总数;D为节点平均度;d(u,v)表示节点u与v之间的欧氏距离;α表示随机网络中长距离链路数与短距离链路数的比值,它是取自(0,1]的实数;L表示所有节点的最大距离上限。本实验将L设置为100 km,把α设置为0.18,D设置为5,使其更符合现实中的确定性网络拓扑结构,使用KRTG模型避免了生成的连通图相邻节点距离过近的现象,使节点分布均匀且疏密得当,同时选择合适的组播路由算法生成多源组播路由方案,以提供网络编码构造算法的运行环境 。
3.1 算法有效性测试
在随机性构造算法中用P=(1-t/q)n表示最终生成满秩的全局编码矩阵的概率,其中t为组播信宿数,本文虚拟试播与随机性网络编码构造算法相似,只有q大于组播信宿t才能保证网络可进行编码运算,伽罗华域中q=2m表示伽罗华域的阶数,m为伽罗华域的次数,可见本文的算法对伽罗华域的次数m有一定要求。设置m取3~9,在不同的网络规模下分别仿真本文DLSNC 500次,统计出信宿获得满秩的全局编码矩阵的次数,结果如表1所示。
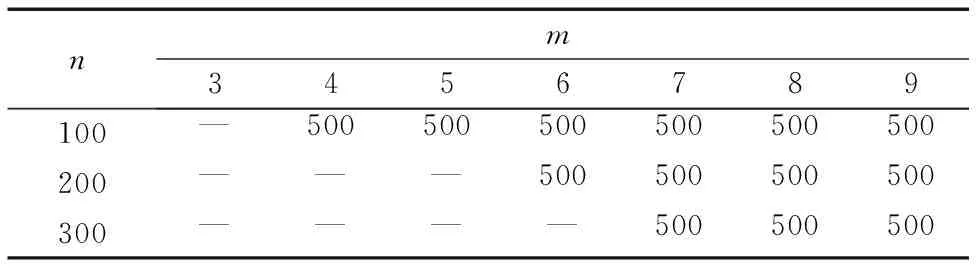
表1 DLSNC获得满秩编码矩阵次数(仿真500次)Tab. 1 Generation times of full rank coding matrix by DLSNC (simulating 500 times)
从表1可以看出:在节点数分别为100、200、300的组播路由方案中,网络规模越大对伽罗华域的次数要求越高,但只要在网络规模小于300,m大于等于7就能保证信宿获得满秩矩阵,所以该算法适用于中等规模的编码网络。
3.2 性能对比
为了验证本文算法的优势,在组播路由方案已知情况下,将本文算法与其他已有构造算法进行比较。设网络规模为200个节点,伽罗华域的次数m依次取5~11,分别进行10 000次实验,并记录信宿接收到满秩全局编码矩阵的次数。通过表2可以发现:文献[11]的算法和文献[12]的算法与伽罗华域的次数m成正比,但是很难百分之百生成满秩全局编码矩阵;文献[10]、文献[15]的算法和本文算法(DLSNC)的成功率与伽罗华域次数m无关,只要伽罗华域次数满足m>lbt就能进行算法的构造,其中t为组播信宿数。
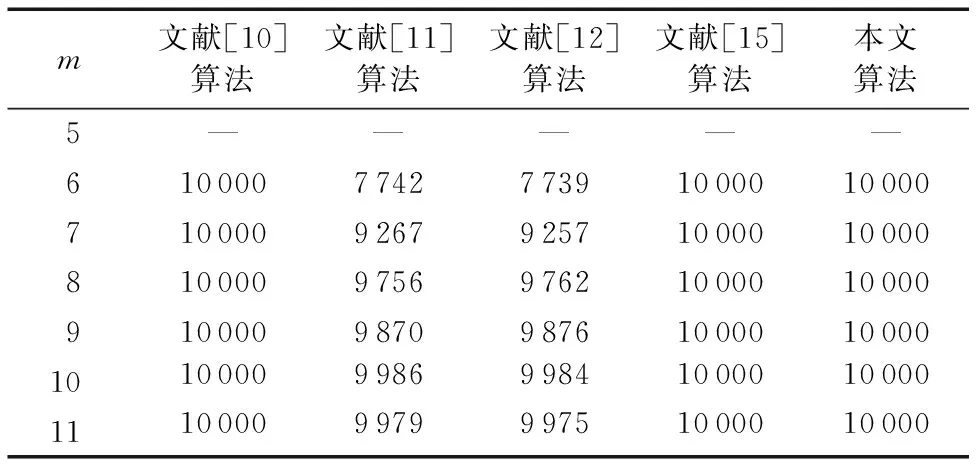
表2 不同构造算法获得满秩编码矩阵次数对比(仿真10 000次)Tab. 2 Generation times comparison of full rank coding matrix by different construction algorithms (simulating 10 000 times)
接下来对本文算法与其他几个算法在收敛时间上进行仿真分析比较。同样使用K均值聚类Waxman随机拓扑模型(KRTG),采用软件NS2模拟多源组播数据信息的传输,在进行多源组播数据的模拟前需要先在Tcl仿真脚本中设置链路带宽为1.6 MB/s,传输的数据分组大小为1.2 MB/s的固定码率(Constant Bit Rate, CBR)流,使其小于设置的带宽容量,其中多余带宽留给传输链路状态分组[26]。物理层选用IEEE802.3u,MAC(Medium Access Control)层协议采用基带冲突检测的载波监听多路访问(Carrier Sense Multiple Access with Collision Detection, CSMA/CD)技术实现媒体访问机制,采用TCP(Transmission Control Protocol),设置时隙宽度为60 μs,调用随机早期检测(Random Early Detection, RED)队列管理协议[26],接口队列类型为Queue/DropTail/PriQueue,对使用网络编码的策略使用优化网络编码协议(Network Coding optimization Scheme based on Microhabitat genetic algorithm, NCSM)。该实验在网络规模n分别为100、175、250、325和400的情况下,分别执行以上算法100次,并通过awk程序统计每次的运行时间并求和,最后将统计的求和结果除以运行总次数,就得到了每种算法在不同网络规模下的平均收敛时间,最后用Matlab画出各算法平均收敛时间与网络规模关系的折线图,结果如图4所示。
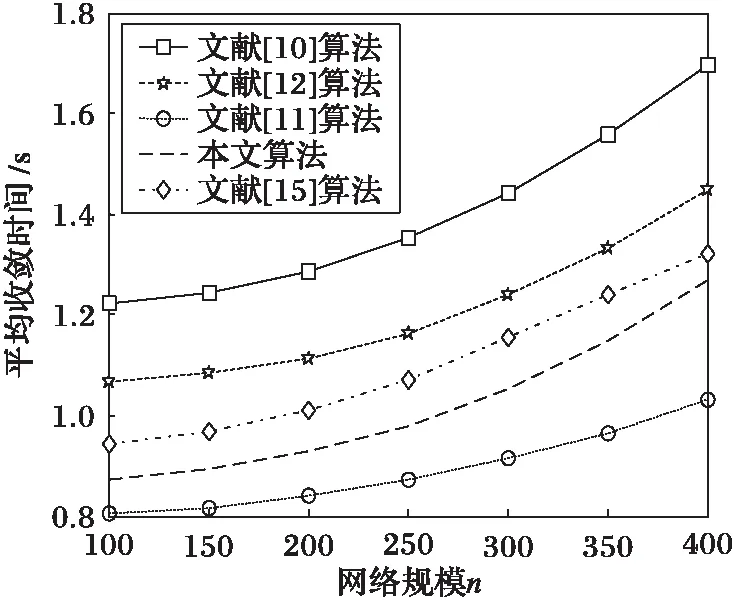
图4 网络编码构造算法收敛时间对比 Fig. 4 Convergence time comparison of network coding construction algorithms
由各算法收敛时间折线图分析得出:虽然在表2中文献[10]的算法和本文算法一样与伽罗华域次数m无关,但前者算法收敛时间较长;文献[15]的算法在各层网络编码节点进行分层多播,需要在信源信宿间反复寻找增广路径,且需要在网络内部节点进行解码,算法复杂度高,收敛时间较长,只有在大规模网络拓扑中,才能充分发挥其性能;而文献[11]算法是一种分布式随机线性网络编码构造算法,且其时间复杂度仅为O[|Vc||D|hs2],所以收敛时间最短[27],适用于网络拓扑变化快的环境中,但是每次群组播都需重构局部编码向量,而且编码成功的概率取决于伽罗华域次数m;作为确定线性编码构造算法,文献[12]算法与本文算法都适用于确定性网络中,但文献[12]算法需要进行多次试播,而本文算法只需进行一次虚拟试播便能确定可行编码方案,所以有更短的收敛时间。
4 结语
针对多源组播网络,给出了确定性逐层构造网络编码算法。通过添加虚拟信源,将多源多宿组播问题转化成单源多宿组播问题,其试播过程就是求解编码方案的过程。本文提出了运用决策树算法寻找目标节点的方法、由上到下逐层构造多源组播网络的线性网络编码方案和修剪枝策略。仿真结果表明了所提算法的可行性和有效性,同时该算法为网络编码组播路由算法与网络编码构造算法相结合的组播策略提供了新的思路和组合方案。
参考文献(References)
[1] AHLSWEDE R, CAI N, LI S-Y R, et al. Network information flow [J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.
[2] KOETTER R, MÉDARD M. An algebraic approach to network coding [J]. IEEE/ACM Transactions on Networking, 2003, 11(5): 782-795.
[3] JAGGI S, SANDERS P, CHOU P A, et al. Polynomial time algorithms for multicast network code construction [J]. IEEE Transactions on Information Theory, 2005, 51(6): 1973-1982.
[4] YEUNG R W. Information Theory and Network Coding [M]. Berlin: Springer-Verlag, 2010: 505-545.
[5] 蒲保兴,王伟平.线性网络编码运算代价的估算与分析[J].通信学报,2011,32(5):47-55. (PU B X, WANG W P. Evaluation and analysis of the computation [J]. Journal on Communications, 2011, 32(5): 47-55.)
[6] 陈超.确定网络编码的安全特性研究[D].南京:南京理工大学,2012:15. (CHEN C. Research on deterministic network coding [D]. Nanjing: Nanjing University of Science and Technology, 2012: 15.)
[7] CHARLES D, JAUTER K, LAUTER K. Signatures for network coding [J]. International Journal of Information and Coding Theory, 2009, 1(1): 3-4.
[8] 王龙翔.基于网络编码的MAC协议研究[D].成都:电子科技大学,2013:12. (WANG L X. Research on MAC protocol based on network coding [D]. Chengdu: University of Electronic Science and Technology of China, 2013: 12.)
[9] LUN D S, MÉDARD M, KOETTER R, et al. On coding for reliable communication over packet networks [J]. Physical Communication, 2008, 1(1): 3-20.)
[10] 付卫平,蒲保兴,刘远军,等.确定性网络编码构造的仿真实现[J].邵阳学院学报(自然科学版),2013,10(1):26-32. (FU W P, PU B X, LIU Y J, et al. Simulation implementation of deterministic construction of network coding [J]. Journal of Shaoyang University (Natural Science Edition), 2013, 10(1): 26-32.)
[11] 魏姗.基于网络编码的分层组播算法研究[D].长沙:中南大学,2012:25. (WEI S. Layered multicast based on network coding [D]. Changsha: Central South University, 2012: 25.)
[12] 蒲保兴,杨路明,王伟平.网络拓扑未知环境下确定性网络编码数据传输[J].电子学报,2009,37(10):2119-2124. (PU B X, YANG L M, WANG W P. A deterministic data transmission approach with network coding under unknown network topology [J]. Acta Electronica Sinica, 2009, 37(10): 2119-2124.)
[13] 靳美丽.基于网络编码的分布式卫星路由算法[D].西安:西安电子科技大学,2013:33-40. (JIN M L. A distributed satellite routing algorithm based on network coding [D]. Xi’an: Xidian University, 2013: 33-40.)
[14] 王白婷.能量有效的无线传感网分簇路由协议研究[D].长春:吉林大学,2016:25. (WANG B T. Research on energy efficient clustering routing protocol for wireless sensor networks [D]. Changchun: Jilin University, 2016: 25.)
[15] WIDMER J, CAPALBO A, ANTA A F, et al. Efficient interlayer network codes for fair layered multicast streaming [J]. IEEE/ACM Transactions on Networking, 2015, 23(4): 1107-1120.
[16] TASSI A, CHATZIGEORGIOU I, VUKOBRATOVIC D. Resource-allocation frameworks for network-coded layered multimedia multicast services [J]. IEEE Journal on Selected Areas in Communications, 2015, 33(2): 141-155.
[17] CHENG M X, YE Q, CHENG X, et al. Network coding and coding-aware scheduling for multicast in wireless networks [C]// ICC 2015: Proceedings of the 2015 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2015: 5703-5708.
[18] KWON M, PARK H. Network coding-based distributed network formation game for multi-source multicast networks [C]// ICC 2017: Proceedings of the 2017 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2017.
[19] 陈仁亮,韩亮,董超,等.基于随机网络编码的转发速率在线控制策略[J].军事通信技术,2016,37(1):8-11. (CHEN R L, HAN L, DONG C, et al. Online forwarding rate controlling strategy based on random network coding [J]. Journal of Millitary Communications Technology, 2016, 37(1): 8-11.)
[20] 蒲保兴,杨路明,王伟平.线性网络编码的导出与扩展[J].软件学报,2011,2(3):558-571. (PU B X, YANG L M, WANG W P. Generation and extension of linear network coding [J]. Journal of Software, 2011, 22(3): 558-571.)
[21] LANGBERG M, SPRINTSON A, BRUCK J. The encoding complexity of network coding [J]. IEEE/ACM Transactions on Networking, 2006, 14(SI): 2386-2397.
[22] 尹吉星,任平安.基于网络编码的多播路由算法研究[J].计算机技术与发展,2014,24(5):9-82. (YIN J X, REN P A. Multicast routing algorithm based on network coding [J]. Computer Technology and Development, 2014, 24(5): 79-82.)
[23] 徐光宪,赖俊宁.新型集中式网络编码组播路由算法[J/OL].计算机科学与探索(2016- 11- 01) [2017- 02- 22]. http://d.g.wanfangdata.com.cn/Periodical_pre_cfe78018-9cd1-45c6-8e0b-a99f3e67cab2.aspx. (XU G X, LAI J N. Centralized network coding multicast routing algorithm [J/OL]. Journal of Frontiers of Computer Science and Technology (2016- 11- 01) [2017- 02- 22]. http://d.g.wanfangdata.com.cn/Periodical_pre_cfe78018-9cd1-45c6-8e0b-a99f3e67cab2.aspx.)
[24] 潘峰.基于C5.0决策树算法的考试结果预测研究[J].微型机与应用,2016,35(8): 68-70. (PAN F. The test results prediction research based on C5.0 decision tree algorithm [J]. Microcomputer & Its Applications, 2016, 35(8): 68-70.)
[25] 蔡慧,刘洪波,韩国栋,基于K均值聚类的随机网络拓扑模型[J].计算机工程与设计,2009,30(5):1089-1091. (CAI H, LIU H B, HAN G D. Random network topology model based on K-means [J]. Computer Engineering and Design, 2009, 30(5): 1089-1091.)
[26] YUAN N Q, JIANG T, BAI S, et al. Dynamic network model analysis based on communication network [J]. Advanced Materials Research, 2014, 989/990/991/992/993/994: 2639-2642.
[27] 杨建业.动态网络拓扑结构变化的多角度度量[D].西安:西安电子科技大学,2013:9. (YANG J Y. Multi-aspects measurement of topological structure in dynamic networks [D]. Xi’an: Xidian University, 2013: 9.)
This work is partially supported by National Science and Technology Support Program of China (2013BAH12F02), the Liaoning Colleges and Universities Fund for Distinguished Young Scholars (LJQ2012029).
XUGuangxian, born in 1977, Ph. D., professor. His research interests include information theory, network coding.
ZHAOYue, born in 1992, M. S. candidate. Her research interests include information theory, network coding, information security.
LAIJunning, born in 1992, M. S. His research interests include network coding, information security.

